橡胶阻尼式扭转减振器固有频率计算与测试方法的研究

上官文斌，魏玉明，赵 旭，荣俊伟，王亚杰

(1.华南理工大学机械与汽车工程学院，广东广州510641；2.宁波拓普集团股份有限公司，浙江宁波315800)

橡胶阻尼式扭转减振器固有频率计算与测试方法的研究

上官文斌1，2，魏玉明1，赵 旭1，荣俊伟2，王亚杰2

(1.华南理工大学机械与汽车工程学院，广东广州510641；2.宁波拓普集团股份有限公司，浙江宁波315800)

设计了橡胶试片静动态剪切特性实验夹具，测试得到了橡胶试片在不同压缩比下的静动态剪切特性。建立了表征橡胶试片静动态剪切特性的Kelvin-Voigt本构模型、Maxwell本构模型和分数导数本构模型，提出了由实验测得的橡胶试片剪切特性曲线来识别各模型参数的方法。给出了基于这3种本构模型计算橡胶阻尼式扭转减振器固有频率的方法，计算了一扭转减振器固有频率，并与测试值进行对比。结果表明：基于Kelvin-Voigt模型计算得到的固有频率不随激振振幅的变化而变化，不能表征振幅相关性，而 Maxwell模型和分数导数模型计算固有频率能表征振幅相关性。大振幅激励时，利用 Maxwell模型计算的固有频率与实测值的误差较大；在各种激励振幅下，利用分数导数模型可较准确计算出减振器的固有频率。

扭转减振器；橡胶；模型参数测试与辨识；固有频率测试

引 言

减少发动机曲轴扭转振动的常用方法是在曲轴前端安装减振器［1］。橡胶阻尼式扭转减振器因为结构简单、成本较低，而广泛应用于乘用车发动机的曲轴减振。橡胶阻尼式扭转减振器的固有频率是其最重要的性能参数之一，在扭转减振器惯量环的惯量一定的情况下，其固有频率与橡胶圈扭转刚度、阻尼等有关。而橡胶圈扭转刚度、阻尼跟橡胶圈压缩比、激振频率、激振振幅密切相关［2］。由于橡胶阻尼式扭转减振器固有频率受多种因素影响，以往的橡胶阻尼式扭转减振器的设计开发是一个不断试验、修正的复杂过程。目前关于橡胶阻尼式扭转减振器固有频率计算方面的研究工作较少。因此，研究橡胶阻尼式扭转减振器固有频率计算方法具有较重要意义。

在橡胶动态黏弹性力学特性的研究中，广泛应用Kelvin-Voigt，Maxwell、分数导数等力学模型［3-5］。Berg等［6］将Maxwell力学模型应用于轨道车辆橡胶隔振器动态特性计算，并取得了良好的效果。Östberg等［7］使用分数导数模型对一橡胶隔振器进行建模，提出一种计算空心圆柱形橡胶隔振器动刚度的方法。

本文测试了用于扭转减振器橡胶圈的橡胶试片在不同压缩比下，静态力与位移关系特性，测试了橡胶试片动态剪切特性与激振频率的关系。进行了在不同角位移激励下，橡胶阻尼式扭转减振器固有频率的测试。分别用Kelvin-Voigt，Maxwell，分数导数模型描述橡胶材料的黏弹性特性，通过测试得到的橡胶试片的静动态特性，经计算分析，得到了Kelvin-Voigt，Maxwell，分数导数本构模型中的参数。利用这3种模型计算橡胶扭转减振器的固有频率，并和实验值进行了对比。

1 扭转减振器固有频率和橡胶试片静动态特性实验

1.1 固有频率测试实验

橡胶阻尼式扭转减振器结构和固有频率测试实验分别见图1和2。

固有频率测试时，扭转减振器的惯量环处于自由状态，轮毂与实验台的激振轴紧固联接。试验台激振轴对轮毂产生恒定振幅角位移激励。在激振轴与惯量环外缘安装两个加速度传感器，测量其切向方向加速度。对惯量环上的加速度与激振轴上的加速度相除，可得到一传递函数，其幅值的峰值所对应的频率为减振器固有频率。图3某减振器固有频率测试曲线，由图可见，在频响函数达到峰值时，滞后角为-90°，测试得到的固有频率为357 Hz。

图1 橡胶阻尼式扭转减振器Fig.1 Rubber damped torsional vibration absorber

图2 橡胶阻尼式扭转减振器固有频率测试实验Fig.2 Measurement of natural frequency of rubber damped torsional vibration absorber

图3 一扭转减振器频率函数测试曲线Fig.3 Measured frequency response function of a torsional vibration abosrber

1.2 橡胶试片剪切试验

扭转减振器工作时，联接轮毂和惯量环的橡胶圈每一小段微元均处于剪切状态。为了表征其受力情况，得到橡胶阻尼式扭转减振器中橡胶圈的静、动态特性参数，本文设计了橡胶试片剪切实验工装，进行了与扭转减振器相同材料的橡胶试片静动态特性实验。

橡胶试片剪切实验工装见图4。实验工装包括运动块(1)、锁紧块(4，7)、转接块(5)、夹板(2，10)、橡胶试片(8)、垫片(9)和紧固螺栓。在MTS831弹性体实验台上进行橡胶试片静态剪切及动态剪切实验。运动块(1)与MTS弹性体实验台运动端联接，锁紧块(4，7)通过转接块(5)与MTS弹性体实验台固定端联接。在运动块(1)和两个锁紧块(4，7)中间放入两个橡胶试片。两个橡胶试片对称布置。在两个锁紧块外部套上两个夹板(2，10)。橡胶试片压缩量与压缩前的厚度之比定义为压缩比。在两个夹板中间可安装垫片，通过不同厚度垫片的组合可以实现不同的压缩比。

图4 橡胶试片剪切实验工装三维模型Fig.4 3D model of test fixture for measuring shear performance of a rubber specimen

试验橡胶试片的材料和尺寸参数见表1。其中A0和d0为橡胶试片压缩前的面积和厚度。

表1 橡胶试片材料和尺寸参数Tab.1 materials and sizes of rubber specimen

在橡胶试片准静态试验时，对橡胶试片的运动块施加低频稳态简谐位移激励，测试工装固定端力随位移激励的变化关系曲线。为了尽量减少黏性力影响，应采用较低激振频率和较大激振振幅。本实验采用激振频率为0.2 Hz，振幅为5 mm的稳态简谐位移激励，分别进行压缩比从20%到50%的准静态剪切实验，记录橡胶试片的力与位移关系如图5所示。

图5 准静态剪切试验力与位移关系曲线Fig.5 Measured shear force and displacement of rubber specimen

在橡胶试片动态剪切试验时，为了尽量减小橡胶块内部摩擦力的影响，应采用较小激振振幅。本实验的激振振幅为0.1 mm，激振频率范围为5～500 Hz。动态剪切实验时，记录橡胶试片剪切动刚度随激振频率的变化关系曲线，如图6所示。橡胶试片静动态特性的实验方法和数据处理方法可参考文献［8］。

图6 动态剪切试验动刚度与激振频率关系曲线Fig.6 Measured dynamic shear stiffness versus excitation frequency of rubber specimen

2 橡胶阻尼式扭转减振器力学模型

将扭转减振器的轮毂和惯量环简化为转动惯量为Jh和Ji的惯量盘，其扭振角分别为θh和θi，如图7所示。将橡胶圈简化为具有刚度和阻尼的黏弹性元件，采用不同方法表征黏性特性时，就得到不同力学模型。

图7 橡胶阻尼扭转减振器的等效力学模型Fig.7 Equivalent mechanic models for rubber damped torsional vibration dampers

2.1 Kelvin-Voigt模型

将橡胶圈等效为弹簧和阻尼单元并联，得到扭转减振器Kelvin-Voigt力学模型，如图7(a)所示［3］。图中，KKV为扭转刚度，CKV为阻尼。基于Kelvin-Voigt力学模型，扭转减振器惯量环的振动方程为

2.2 Maxwell模型

扭转减振器Maxwell力学模型如图7(b)所示［3-5］，轮毂和惯量环间的相互作用力矩为弹性扭矩、黏弹性扭矩、摩擦扭矩的叠加。其中Ke为弹性扭转刚度，KMv为黏弹性扭转刚度，CMv为黏性阻尼，Tf为橡胶摩擦扭矩。摩擦扭矩由橡胶分子之间的摩擦产生，与频率无关，只与橡胶变形量有关［3］。扭转减振器Maxwell力学模型可简化为刚度为KMeq的弹簧、阻尼为 CMeq的弹性、阻尼单元和摩擦单元并联的等效力学模型，等效扭转刚度和阻尼分别为：

式中 ω为作用于减振器轮毂处的激振频率。

基于Maxwell力学模型，减振器惯量环的振动方程为

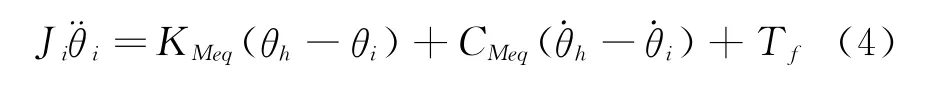
2.3 分数导数模型

橡胶阻尼式扭转减振器分数导数力学模型如图7(c)所示［3］。轮毂和惯量环间的相互作用力矩为弹性扭矩、黏弹性扭矩、摩擦扭矩的叠加。弹性扭矩、摩擦扭矩与Maxwell力学模型一致。黏弹性力矩在的分数导数模型中为［4］

式中 B为黏弹性扭矩系数，α为分数导数阶，其取值范围为0＜α＜1，Dα(·)表示对(·)的α阶导数。

基于分数导数力学模型，扭转减振器惯量环的振动方程为

3 橡胶本构模型参数的确定

在橡胶阻尼式扭转减振器中，由橡胶圈提供的扭转刚度和阻尼与橡胶材料的配方、压缩比和橡胶圈的尺寸有关。为了消除橡胶圈的尺寸对橡胶圈材料动态性能的影响，建立橡胶圈材料的Kelvin-Voigt本构模型、Maxwell本构模型和分数导数本构模型，分别见图8(a)，(b)，(c)所示。

3.1 Kelvin-Voigt本构模型参数的确定

在橡胶Kelvin-Voigt模型中试片剪切动刚度为

式中 kKV和cKV分别橡胶试片Kelvin-Voigt模型中的剪切刚度和剪切阻尼。

图8 橡胶本构模型Fig.8 Rubber constitutive model

由动态剪切实验测得的橡胶试片剪切动刚度随激振频率变化的函数关系曲线，根据最小二乘法拟合即可得到kKV和cKV。压缩比为50%的动刚度测试及拟合曲线如图9所示。

图9 Kelvin Voigt模型动刚度测试及拟合曲线Fig.9 Measured dynamic stiffness versus frequency of rubber specimen，and the fitted curve using Kelvin-Voigt model

橡胶材料Kelvin-Voigt模型中，其剪切模量GKV可由橡胶试片的弹性刚度kKV计算得到，黏性系数ηKV可由橡胶试片剪切阻尼cKV计算得到。

图10为单个橡胶试片剪切状态示意图，橡胶弹性剪切模量为

图10 单个橡胶试片剪切状态示意图Fig.10 The shear deformation of a rubber specimen

式中 τKV为橡胶弹性剪切应力，γ为橡胶剪切应变，FKV为试片弹性剪切力，A为试片压缩后与实验工装的接触面积，x为试片剪切位移，d为试片压缩后的厚度，分母中的2代表有两块试片同时进行试验。

橡胶试片压缩比为

假设橡胶试片在压缩过程中体积保持不变，得

将式(9)和(10)代入式(8)，得

同理，由橡胶试片剪切阻尼cKV计算得到橡胶试片的Kelvin-Voigt本构力学模型的黏性系数ηKV，即

由橡胶试片动态剪切实验计算得到的橡胶试片Kelvin-Voigt模型参数和本构模型参数如表2所示。对弹性剪切模量GKV和单元黏性系数ηKV与压缩比的关系进行最小二乘拟合，得到如下关系式：

表2 橡胶试片Kelvin-Voigt模型和本构模型参数Tab.2 Parameters of Kelvin-Voigt model and constitutive model

3.2 Maxwell本构模型参数的确定

当橡胶试片压缩比已知时，由准静态实验，测试得到作用于橡胶试片的剪切力与位移激励关系曲线，根据参考文献［3］，可求解得到橡胶试片的弹性刚度ke、最大摩擦力Ffmax和1/2最大摩擦力时的位移x1/2。压缩比为20%时，准静态实验所测试得的一组剪切力与位移激励函数关系曲线，如图11所示。

图11 剪切力与位移关系曲线Fig.11 Shear force versus displacement

由橡胶试片弹性刚度、最大摩擦力、1/2最大摩擦力时的位移，可计算得到Maxwell本构模型中的弹性剪切模量Ge、最大摩擦应力τfmax、1/2最大摩擦应力时的应变γ1/2。

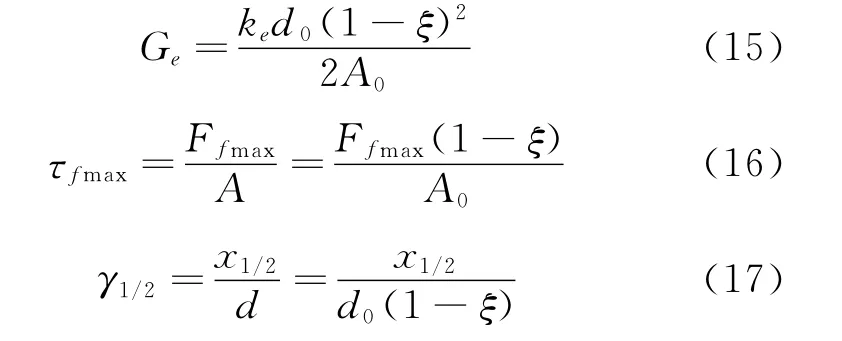
在不同的试片压缩比下，由橡胶试片准静态剪切实验得到的力和位移关系，计算得到的Maxwell橡胶材料本构模型参数如表3所示。对表3的计算结果，应用最小二乘方法，可拟合得到Maxwell本构模型中的参数与橡胶试片压缩比的关系为：

在橡胶试片Maxwell模型中，当位移激励幅值较小时，可忽略摩擦力影响，橡胶试片动态剪切刚度随激振频率变化的函数关系为［6］

式中 kMv，cMv分别为橡胶试片Maxwell模型中黏弹性单元的剪切刚度和剪切阻尼。利用最小二乘方法，由动态剪切实验测得的橡胶试片剪切动刚度随激振频率变化关系，即可得到kMv和cMv。压缩比为50%时，橡胶试片剪切动刚度随激振频率变化测试曲线与拟合曲线如图12所示。

橡胶Maxwell本构模型中黏弹性单元的参数，GMv和ηMv，可由橡胶试片黏弹性剪切刚度 KMv和黏弹性剪切模量CMv计算得到：

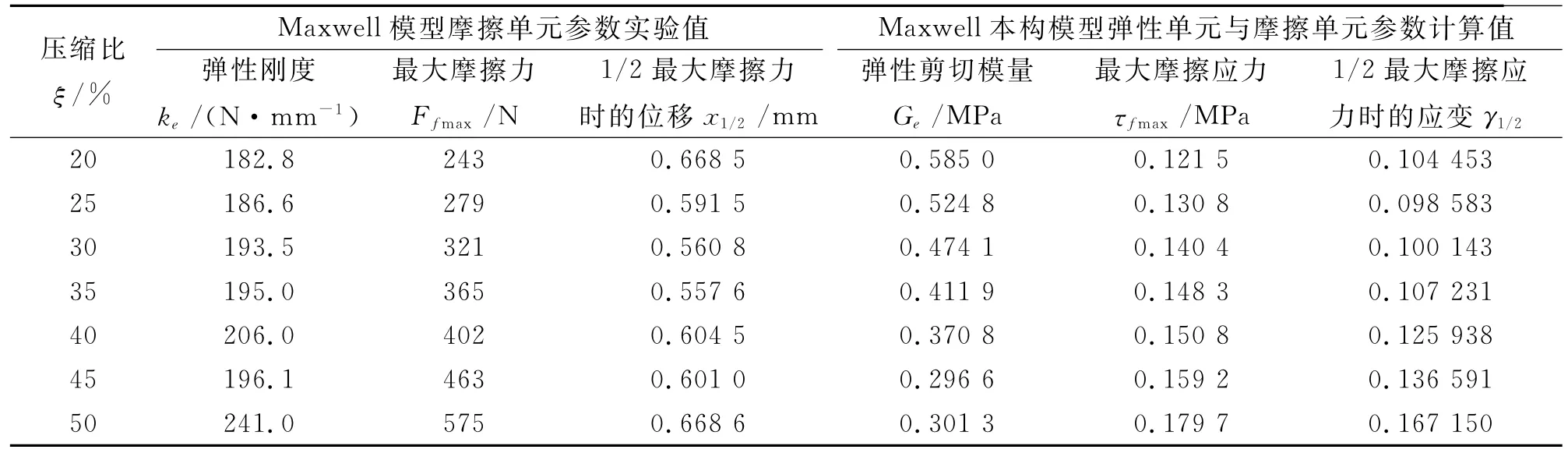
表3 橡胶试片Maxwell模型摩擦单元参数、Maxwell本构模型中弹性单元与摩擦单元参数Tab.3 Parameters for friction element in Maxwell model of rubber specimen，and parameters for elastic element and friction element in Maxwell constitutive model

图12 Maxwell模型动刚度测试及拟合曲线Fig.12 Measured dynamic stiffness versus frequency of rubber specimen，and the fitted curve using Maxwell model

在一定的压缩比下，计算得到的橡胶试片Maxwell模型中黏弹性单元的参数如表4所示。对Maxwell本构模型黏弹性剪切模量GMv与黏性系数ηMv与压缩比的关系进行最小二乘拟合，得到以下关系式：

表4 橡胶试片Maxwell模型中黏弹性单元参数Tab.4 Parameters for visco-elastic element in Maxwell model

3.3 分数导数本构模型参数的确定

橡胶试片分数导数本构模型中的弹性剪切模量Ge、最大摩擦应力τfmax和1/2最大摩擦应力时的应变γ1/2与Maxwell橡胶试片力学模型中的参数相同。在橡胶试片动态剪切实验中，当位移激励幅值较小时，分数导数橡胶试片力学模型可忽略摩擦力影响，橡胶试片动态剪切刚度随激振频率变化的函数关系为

式中 b为分数导数橡胶模型中橡胶试片黏弹性系数，α为分数导数橡胶模型中橡胶试片分数导数阶。由动态剪切实验测得的橡胶试片剪切动刚度随激振频率变化的函数关系曲线，最小二乘法拟合得到b和α。压缩比为50%时，橡胶试片剪切动刚度随激振频率变化测试曲线与拟合曲线如图13所示。

图13 分数导数模型动刚度测试及拟合曲线Fig.13 Measured dynamic stiffness versus frequency of rubber specimen，and the fitted curve using fractional derivative model

橡胶材料本构模型中的单元黏弹性系数m可由橡胶试片中的黏弹性系数b计算得到

计算得到的分数导数模型和分数导数本构模型中的常数见表5。对单元黏弹性系数m和分数导数阶α与压缩比的关系，进行最小二乘拟合，拟合关系式为：

表5 分数导数模型中黏弹性单元模型参数Tab.5 Parameters for visco-elastic element in fractional derivate model

4 橡胶阻尼式扭转减振器固有频率计算

4.1 扭转减振器扭转刚度与阻尼的计算

通过橡胶试片准静态剪切实验和动态剪切实验得到了3种不同橡胶模型的参数。各种模型中的模型参数与橡胶试片尺寸无关。由3种橡胶本构模型的参数，和扭转减振器尺寸参数，可计算得到扭转减振器的刚度和阻尼，进而用于扭转减振器固有频率的计算。

任意轮毂形状的橡胶阻尼式扭转减振器如图14所示，扭转刚度K与橡胶弹性剪切模量G的关系 为［9］

式中 r1(x)为沿橡胶圈轴向变化的轮毂外半径，r2(x)为沿橡胶圈轴向变化的惯量环内半径，L为橡胶圈宽度。分别将橡胶试片Kelvin-Voigt模型中弹性剪切模量GKV、Maxwell力学模型弹性剪切模量Ge和黏弹性剪切模量GMv、分数导数力学模型弹性剪切模量Ge带入式(29)中，即可得到扭转减振器Kelvin-Voigt模型扭转刚度KKV、Maxwell模型弹性扭转刚度Ke和黏弹性扭转刚度KMv、分数导数模型弹性扭转刚度Ke。

图14 任意轮毂形状橡胶阻尼式扭转减振器Fig.14 Cross-section of a torsional vibration absorber

扭转减振器阻尼C与橡胶材料的黏性系数η的关系为

将橡胶试片Kelvin-Voigt本构模型单元黏性系数ηKV、Maxwell本构学模型单元黏性系数ηMv带入式(30)中，即可得到扭转减振器Kelvin-Voigt力学模型阻尼CKV、Maxwell力学模型黏性阻尼CMv。

由公式(2)可得橡胶阻尼式扭转减振器Maxwell力学模型等效扭转刚度KMeq，由公式(3)可得橡胶阻尼式扭转减振器Maxwell力学模型等效阻尼CMeq。

任意轮毂形状的减振器最大摩擦扭矩Tfmax与最大剪切应力τfmax的关系为

式中 r(x)为橡胶圈内外半径均值。

4.2 基于Kelvin-Voigt模型计算固有频率

当扭转减振器中的橡胶圈的动态特性用Kelvin-Voigt模型来表征时，扭转减振器惯量环的振动方程为公式(1)，其频率的计算公式为

式中 fKVn为橡胶阻尼式扭转减振器Kelvin-Voigt模型中无阻尼固有频率，ζ为阻尼比。由式(32)可得，橡胶阻尼式扭转减振器Kelvin-Voigt力学模型固有频率未考虑幅值相关性，即不同角位移激励计算得到的减振器固有频率均相等。

4.3基于Maxwell模型计算固有频率

当扭转减振器中的橡胶圈的动态特性用Maxwell模型来表征时，扭转减振器惯量环的振动方程为公式(4)。由于Maxwell模型中的等效刚度KMeq和等效阻尼CMeq均与频率相关，因此不能利用公式(4)来直接求解固有频率。可采用在轮毂处加一激励，当振幅一定时，频率在一定的范围内变化，求解扭转减振器惯量环的振动响应，其峰值即为扭转减振器的固有频率。

本文采用中心差分法，求解惯量环的响应。应用有限差分替代位移对时间的导数，采用等时间步长Δt，有：

式中 n为迭代步数。

由式(33)和(34)对惯量环的振动方程(4)在时域进行离散化，并化简，得到惯量环转角迭代计算公式：

摩擦扭矩的迭代计算公式计算方法见参考文献［3］。计算中，惯量环转角迭代公式和摩擦扭矩迭代公式的初始条件为

作用于扭转减振器轮毂处位移激励为单一频率的简谐分量，即

式中 Ae为轮毂处角位移激励幅值，fe为激励频率。

综上所述，基于Maxwell模型，计算扭转减振器固有频率步骤为：

(1)当轮毂激励角振幅为Ae，激励频率为fe时，由式(33)～(37)计算得到扭转减振器的惯量环转角时域响应；

(2)当惯量环转角位移的时域响应稳定后，其幅值为该位移激励下的惯量环稳态响应幅值；

(3)激励振幅Ae不变，改变激励频率fe，可计算不同激励频率下的惯量环稳态响应幅值，其中惯量环最大的稳态响应幅值对应的激励频率，即为在位移激励振幅Ae下，橡胶阻尼式扭转减振器的固有频率。

(4)改变激励振幅Ae，重复计算步骤(1)～(3)，即可计算不同位移激励振幅下橡胶阻尼式扭转减振器的固有频率。

4.4 基于分数导数模型计算固有频率

由于分数导数模型中，表征橡胶黏弹性特性的常数B和α与频率相关，因此不能直接求解固有频率。可利用与4.3节类似的方法求解扭转减振器的固有频率。

对表征橡胶圈的黏弹性力的公式(5)进行时域离 散 化［2］，得

式中 r0为橡胶圈内外半径均值，L0为橡胶圈的宽度，h0为橡胶圈内外半径差。Aj+1为Grunwald系数，定义为

式中 Γ(·)为Gamma函数。

由式(33)，(34)和(38)，对式(6)进行时域离散化，化简得到惯量环转角迭代公式为

4.5 固有频率的计算值与测试值对比

某款橡胶阻尼式扭转减振器的尺寸和惯量参数如表6所示。由3种不同的模型计算得到的该减振器固有频率与测试得到的固有频率对比如图15所示。

表6 橡胶阻尼式扭转减振器尺寸和惯量环惯量参数Tab.6 Parameters for a torsional vibration damper

图15 不同激振角度下的减振器固有频率计算值与测试值对比Fig.15 Measured and calculated natural frequency of a torsional vibration absorber under different oscillation angles

5 结 论

利用建立的扭转减振器的模型，和橡胶材料的本构模型，进行了一款橡胶阻尼式扭转减振器固有频率计算，并与测试值进行了对比。分析结果表明，Kelvin-Voigt模型计算固有频率不随激振振幅的变化而变化，不能很好地反应橡胶的动态特性。Maxwell模型可表征减振器固有频率随激振振幅变化而变化，可较为准确地计算小振幅激励下橡胶阻尼式扭转减振器固有频率，但大振幅激励下固有频率的计算值与实测值的误差较大。分数导数力学模型能够比较准确地计算橡胶阻尼式扭转减振器在各种激励振幅下的固有频率，其相对误差均在10%以内。

［1］Shangguan Wen-Bin，Pan Xiao-Yong.Multi-mode and rubber-damped torsional vibration absorbers for engine crankshaft systems［J］.International Journal of Vehicle Design，2008，47(1/2/3/4)：176—188.

［2］Tarrago Garcia MJ，Kari L.Frequency and amplitude dependence of the axial and radial stiffness of carbonblack filled rubber bushings［J］.Polymer Testing，2007，26：629—638.

［3］Sjoberg M，Kari L.Non-linear behavior of a rubber isolator system using fractional derivatives［J］.Vehicle System Dynamics，2002，37(3)：217—236.

［4］Pritz T.Analysis of four-parameter fractional derivative model of real solid materials［J］.Journal of Sound and Vibration，1996，195(1)：103—115.

［5］吴杰，上官文斌.采用黏弹性分数导数模型的橡胶隔振器动态特性的建模及应用［J］.工程力学，2008，25(1)：161—166.WU Jie，SHANGGUAN Wenbin.Modeling and applications of dynamic characteristics for rubber isolators using viscolastic fractional derivative model［J］.Engineering Mechanics，2008，25(1)：161—166.

［6］Berg M.Anon-linear rubber spring model for rail vehicle dynamics analysis［J］.Vehicle System Dynamics，1998，30(4)：197—212.

［7］Östberg M，Coja M，Kari L.Dynamic stiffness of hollowed cylindrical rubber vibration isolators-The waveguide solution［J］.International Journal of Solids and Structures，2013，50(10)：1 791—1 811.

［8］Shangguan Wen-Bin，Lu Zhen-Hua.Experimental study and simulation of a hydraulic engine mount with fully coupled fluid structure interaction finite element analysis model［J］.Computers&Structures，2004，82(22)：1 751—1 771.

［9］Tarago G MJ，Kari L，Vinolas J，et al Torsion stiffness of a rubber bushing：a simple engineering design formula including the amplitude，dependence［J］.The Journal of Strain Analysis for Engineering Design，2007，42：13—21.

Astudy on method of calculation and measurement for natural frequency of torsional vibration rubber dampers

SHANGGUAN Wen-bin1，2，WEI Yu-ming1，ZHAO Xu1，RONG Jun-wei2，WANG Ya-jie2
(1.School of Mechanical&Automotive Engineering，South China University of Technology，Guangzhou 510641，China；(2.Ningbo Tuopu Group Co.Ltd.，Ningbo 315800，China)

The natural frequency is one of the most performance parameters of a rubber damped torsional vibration dampers(TVD).The natural frequency is determined by the static and dynamic shear properties of the rubber ring of the TVD，and the moment of inertia of the inertia ring.In this paper a special fixture is designed and used for measuring static and dynamic performance of a rubber shear specimen under different compression ratios.Three constructive models，Kelvin-Voigt model，the Maxwell model and the fractional derivative model，for characterizing the rubber viscous properties are described，and the method for obtaining the model parameters in the three constructive models are developed using the measured dynamic performance of a rubber shear specimen.The natural frequency of a TVD is calculated using the three models to characterize the rubber ring of the TVD，and the calculated frequencies are compared with the measurement.It is demonstrated that the natural frequency of the TVD calculated by the Kelvin-Voigt model is constant when the excitation amplitude is increased，which is inconsistent with the measured data.The calculated natural frequency using the Maxwell and the fractional derivative model to describe the rubber ting of a TVD is the excitation amplitude dependent，which is consist with the trend of measured data.But the relative errors between the calculation using Maxwell model and the measurement under the large amplitude excitation are large，and is not be accepted in engineering application.The natural frequency estimated from the fractional derivative model agrees well with the measured data for different excitation amplitudes，and the relative error between the calculation and measurement is less than 10%.

torsional vibration damper；rubbers；measurement and identification of rubber parameters；natural frequency measurement

U464.133+3

A

1004-4523(2015)04-550-10

10.16385/j.cnki.issn.1004-4523.2015.04.007

上官文斌(1963—)，男，博士，教授，博士生导师。E-mail：sgwb@163.com

2013-08-10；

2015-03-30

国家自然科学基金资助项目(51275175，11472107)