抽油泵阀球密度优化研究
狄敏燕,李汉周,张 格
抽油泵阀球密度优化研究
狄敏燕,李汉周,张 格
(江苏油田分公司石油工程技术研究院,江苏扬州225009)
抽油泵的整个工作过程中,阀球的启闭非常频繁,而阀球密度影响着开启压差,制约开启滞后时间及关闭滞后时间。基于流体力学相关理论和质量守恒定律,建立了泵筒内流体的连续性方程及阀球运动微分方程,分析不同阀球密度对滞后开启时间、滞后关闭时间及总滞后时间的影响。计算结果表明:滞后时间随着阀球密度的增大而减小,当密度小于4×103kg/m3时,滞后时间变化迅速;当密度大于4×103kg/m3时,变化缓慢。
抽油泵;游动阀球;密度;滞后时间
泵阀是抽油泵的重要组件,对抽油泵的工作效率有很大影响[1]。泵阀在工作过程中影响泵效的因素主要表现在泵阀充盈程度与漏失量2个方面,而阀球的启闭特性直接关系到泵筒的充满系数与泵的漏失系数[2]。阀球的启闭特性与泵筒内外液柱压差有关,当泵筒内液体压力大于泵筒外的液柱压力时,阀球关闭;当泵筒内的液体压力小于泵筒外液柱压力,且其压差足以克服阀球自重时,阀球开启。由于柱塞上下冲程运动存在死点,使阀球在开启、关闭时存在滞后现象。抽油泵在整个工作过程中,阀球的启闭是非常频繁的,而阀球密度影响着开启压差进而制约滞后时间,所以对阀球密度的优化研究有利于缩短阀球的滞后时间,能使泵腔在很短时间内就充满油液,减少漏失,提高泵效。
1 阀球运动特性
阀罩失效与阀球的频繁撞击密切相关,在阀球开启和关闭时,阀球的速度和加速度变化较大,因而对阀座和阀罩将产生一定的冲击力[3],影响阀罩使用寿命。本文借鉴已有的阀球运动规律研究成果,结合江苏油田的实际情况,对阀球的运动进行分析[4-6]。
1.1 泵筒内液体连续性方程
为了便于模型建立,假设:①泵筒内流体阻力及惯性力对阀球无作用;②泵筒内各点的流体压力、密度均相同;③忽略阀球公转与自转对其运动的影响[7]。建立抽油泵段相应的坐标系,取下死点为坐标原点C,竖直向上为y轴正方向,对应时刻t为0,柱塞运动满足速度不变的往复运动[8-10],其方程为

式中:yz为t时刻柱塞位移,m;S为柱塞冲程,m;t为柱塞运动时间,s;T0为柱塞运动周期,s;N为冲次,min-1。
假设t时刻,泵内流体压力为p,阀球上升高度为h,忽略阀球与阀座所形成的空间体积,泵内流体质量为

式中:Ap为泵筒截面积,m2;Ls为防冲距,m;ρ为在t时刻泵内流体的平均密度,kg/m3。
在t+d t时刻,柱塞运动至yz+d yz,泵内流体密度变为ρ+dρ,此时泵内流体质量为

泵内流体质量增量为d m=mt+dt-mt,略去二阶小项,化简得
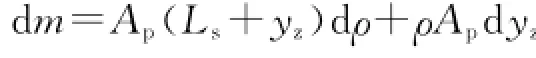
利用流体力学相关理论,在d t内进泵流体质量d m′可以表示为
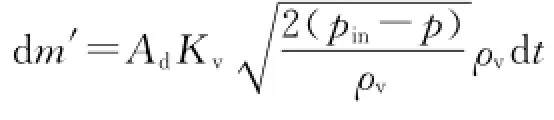
式中:Kv为流量系数;Ad为阀座通孔面积,m2;pin为泵进口压力,Pa;p为泵内流体压力,Pa;ρv为过阀流体密度,kg/m3。
利用质量守恒定律,在d t时间内,d m=d m′,可得进泵流体的连续性方程为
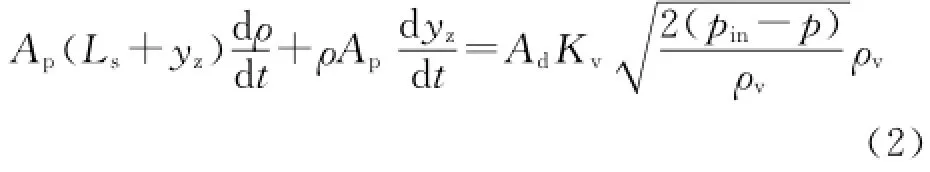
同理,假设游动阀与固定阀参数一样。游动阀开启后抽油泵排油,根据质量守恒定律,单位时间内经过阀隙流入油管内的原油质量与泵筒内减少的原油质量相等。经过公式推导,确定出了泵筒内液体连续流动方程为
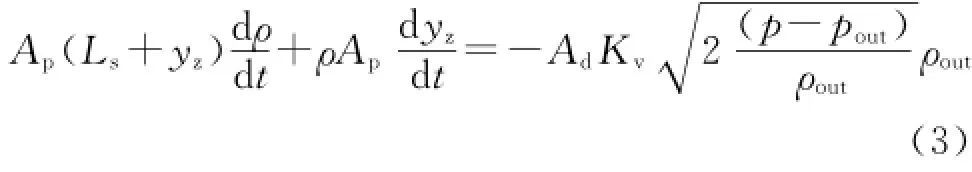
式中:pout为泵出口压力,Pa;ρout为游动阀出口流体密度,kg/m3。
把泵内的流体等效为温度不变的理想状态下的气体以及不可压缩的液体,则流体的密度与压力之间的关系式为

式中:V1为标准大气压下的气体体积,m3;V2为不可压缩液体的体积,m3;V′1为压力p下的气体体积,m3;p0为标准大气压强,取0.1 MPa;R为气油比,m3/m3;ρ0为原油密度,kg/m3;ρ1为标准大气压下的气体密度,为1.293 kg/m3。
将式(4)分别代入式(2)~(3),可分别得到上冲程与下冲程泵内压力与时间之间的关系式,从而得到泵内压力的变化规律。
1.2 阀球运动微分方程
抽油泵固定阀结构如图1所示。在斜井中,抽油泵轴线与铅垂线形成一定角度φ,忽略阀球与液体间的摩擦阻力,建立的固定阀、游动阀球运动微分方程[4-6]为
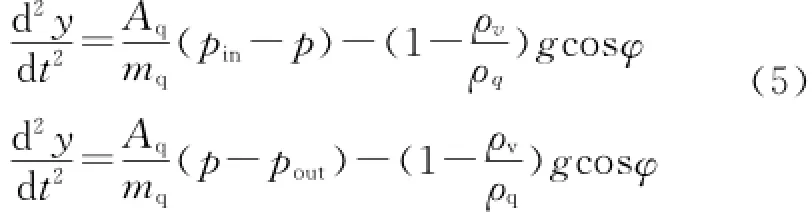
式中:Aq为阀球截面积,m2;mq为阀球质量,kg;ρq为阀球密度,kg/m3;φ为泵的倾斜角,(°)。
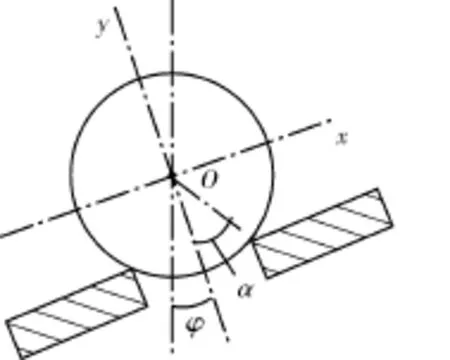
图1 抽油泵固定阀结构
1.3 泵筒内压力变化规律
抽油泵处于上冲程时,柱塞由下死点向上运动,固定阀并未立即开启,存在滞后现象。当固定阀球所受的液体举升力能够克服其重力与浮力差时,固定阀开启。同理,抽油泵处于下冲程时,柱塞由上死点向下运动,游动阀并未立即开启,也存在滞后现象。当游动阀球所受的液体举升力能够克服其重力与浮力差时,游动阀开启。
假设密封处为点接触,由静力学平衡条件求得固定阀和游动阀的开启压差和开启压力分别为
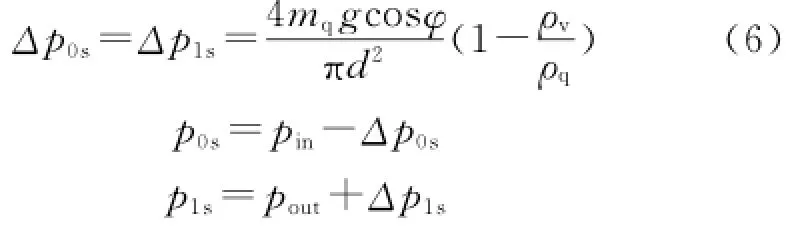
式中:Δp0s为固定阀的开启压差,Pa;Δp1s为游动阀的开启压差,Pa;p0s为固定阀开启时泵筒内的液体压力,Pa;p1s为游动阀开启时泵筒内的液体压力,Pa;d为阀座的通径,m。
泵筒内液体压力变化规律如图2,可以将泵筒内液体压力随时间的变化规律划分为如下6个区间:

图2 泵筒内液体压力变化规律
1)当0≤t≤tcd时(tcd为游动阀滞后关闭时间),上冲程开始,此时固定阀未开启,游动阀滞后关闭。由于此时压力差近似为零,阀球与流体的相对速度很小,忽略游动阀球受到的流体阻力,考虑阀球受到流体的浮力,由于高效泵阀罩有导轨的导向作用,所以游动阀球做斜向运动,求解式(5)~(6)可得游动阀滞后关闭时间为

式中:h0为阀球的升程。固定阀滞后关闭时间t1d=tcd。
2)当tcd≤t≤tcd+t0s时,由于阀未开启,式(2)右边项为零。其中,t0s为固定阀的滞后开启时间;p0s为固定阀的开启压力。当t=tcd时,ρ=ρout;根据式(2)求解得

则压力的解析式为

式中:pout为ρ=ρout时的气液混合流体压力。
由式(4)可计算得

将p0s代入式(9),得到固定阀滞后开启时间为

3)当tcd+t0s≤t<T0/2时,固定阀开启,则压力由式(2)~(4)解得。当t=tcd+t0s时,p=p0s;而后,阀球经过一段时间后相对于阀罩静止,且此时泵内外压力差稳定,进口流速不变,式(2)中的密度不变,化简可得

式(11)可以求解稳定后的泵内压力,此时泵内压力p已经非常接近pin,因此默认为下冲程开始时p=pin。
4)当T0/2≤t≤T0/2+tcd时,下冲程开始,此时游动阀球未开启,固定阀球滞后关闭。同理,忽略固定阀球受到的流体阻力,考虑阀球受到流体的浮力,所以固定阀球做斜向的运动。
5)当T0/2+tcd<t≤T0/2+tcd+t1s时,此时是游动阀开启前,固定阀关闭后的液体压缩增压段。与上述第2阶段同理,式(3)右边项为零。其中,t1s为游动阀的滞后开启时间;p1s为游动阀的开启压力。当t=T0/2+tcd时,ρ=ρin;根据式(3)求解得

类似地,可得到游动阀滞后开启时间为
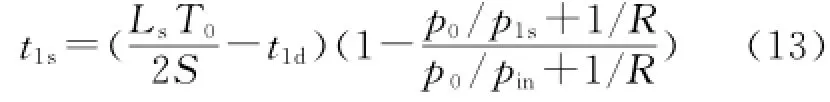
6)当T0/2+tcd+t1s≤t<T0时,游动阀开启,则压力由式(3)~(4)解得。同理,阀球经过一段时间后相对于阀罩静止,且此时泵内外压力差稳定,出口流速不变,式(3)中的密度不变,化简可得

式(14)可以求解稳定后的泵内压力,此时泵内压力p已经非常接近pout,因此默认为下冲程结束时p=pout。
综上所述,由图2以及上述的分析简化结果可见,确定泵筒内液体压力变化规律的关键是确定各个区间的时间界限。泵阀的滞后开启时间和滞后关闭时间可根据上述的初始条件确定。
2 阀球密度对滞后时间的影响
由前述可知阀球的滞后时间分为:游动阀滞后开启时间t1s、滞后关闭时间tcd、总滞后时间t1s+tcd;固定阀滞后开启时间tos、滞后关闭时间t1d、总滞后时间tos+t1d。为了分析阀球密度对滞后时间的影响,针对游动阀罩,阀球的结构参数与固定阀罩、阀球不同,本文分3种情况进行讨论:游动阀球密度为定值;固定阀球密度为定值;两阀球密度同时变化。
采用江苏油田的现场生产数据[11-12],固定阀球参数为r=0.022 m、h=0.029 m、d=0.040 m;游动阀球参数为r=0.009 m、h=0.013 m、d=0.016 m;其他参数为Ls=0.6 m、N=6、S=2.1 m、R=5 m3/m3、pin=2MPa、pout=16MPa、ρv=800 kg/m3、φ=45°。滞后时间随阀球密度的变化关系如图3~7所示。

图3 不同密度下固定阀滞后时间

图4 固定阀总滞后时间放大图

图5 不同密度下游动阀滞后时间
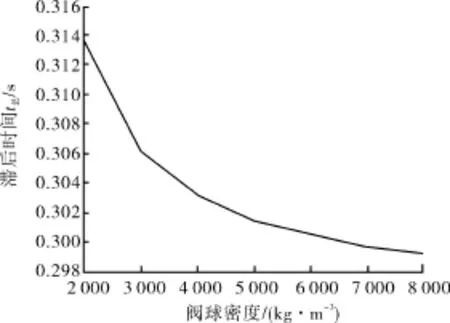
图6 游动阀总滞后时间放大图

图7 两阀球密度同时变化时总滞后时间曲线
由图3~7可以看出:随着密度的增大,固定阀、游动阀的滞后开启时间几乎不变,滞后关闭时间减小,总滞后时间减小;总滞后时间随着阀球密度的增大而减小,当密度小于4×103kg/m3时,总滞后时间变化迅速;当密度大于4×103kg/m3时,总滞后时间变化缓慢,阀球密度对滞后时间影响不大。因此,最佳的阀球密度应根据现场要求(例如防腐性、耐磨性等)去选择ρ≥4×103kg/m3的某一个值。
3 结论
1)运用流体力学相关理论和质量守恒定律,建立了进泵流体和泵内流体的连续性方程及阀球运动微分方程。将泵内流体等效为温度不变的理想状态下的气体以及不可压缩的液体,建立了流体密度与压力的数学模型;结合泵筒内液体压力变化曲线,分析了不同工况下压力随时间的变化规律,得到游动阀、固定阀的滞后关闭时间、滞后开启时间。
2)滞后时间随着阀球密度的增大而减小,当密度小于4×103kg/m3时,滞后时间变化迅速;当密度大于4×103kg/m3时,滞后时间变化缓慢,阀球密度对滞后时间影响不大。所以,最佳的阀球密度应根据现场要求选择ρ≥4×103kg/m3的某一个值。
[1]杨国安,乔舰,宋征,等.钻井泵阀寿命分析[J].振动与冲击,2010,29(1):58-61.
[2]刘富.有杆抽油泵系统工作行为仿真研究[D].南充:西南石油学院,2003:68-74.
[3]郑俊德,曹广胜.聚合物驱泵阀运动规律的试验研究[J].石油矿场机械,1999,28(1):25-28.
[4]葛占玉,鲁延丰.抽油泵泵阀运动规律研究[J].石油大学学报,1995,19(1):66-69.
[5]屈成亮.定向井抽油泵水力分析与实验研究[D].大庆:东北石油大学,2011:26-32.
[6]李凌川,李明忠,王卫阳,等.基于FLUENT的有杆泵抽油流场数值研究[J].当代化工,2013,42(8):1181-1184.
[7]高文凯,梁政,钟功祥,等.往复泵自动球阀运动规律数学模型及计算[J].石油矿场机械,2006,35(1):5-9.
[8]高春红.三次采油区块抽油机载荷和抽油泵失效研究[D].大庆:大庆石油学院,2010:11-16.
[9]吴建军,綦耀光,刘新福,等.基于Simulink的抽油泵泵阀运动规律仿真[J].石油机械,2011,39(1):32-35.
[10]万国强,于大.有杆抽油泵固定阀阀球运动规律模拟分析[J].西南石油大学学报,2013,35(4):165-172.
[11]李汉周,杨海滨,石建设,等.变螺距双螺旋气锚的研制与应用[J].钻采工艺,2013,36(6):89-91.
[12]张文华,高兰,朱剑飞.固定阀球密度对抽油泵进油的影响[J].石油钻采工艺,2003,25(S1):33-37.
Research of Oil Well Pump by Eensity of Valve’s Ball
DI Minyan,LI Hanzhou,ZHANG Ge
(Engineering Technology Research Institute,Jiangsu Cilfield Branch Company,Yangzhou 225009,China)
In the whole process of the oil well pump,opening and closing of the valve ball are very frequent,but the valve ball density affects the open differential pressure and restricts its retardation time and down time.Based on fluid mechanics theory and the law of conservation of mass,continuity equation of fluid into the pump and differential equation of movement of the valve ball is established,and the effect of different density of valve ball on its retardation time and down time is analyzed.The calculation results show that its retardation time and down time is reduced with the increase of the density of the valve ball.When the density is less than 4×103kg/m3,its retardation time and down time changes quickly;when the density is greater than 4×103kg/m3,its retardation time and down time changes slowly.
oil well pump;traveling valve’s ball;density;down time
TE933.3
A
10.3969/j.issn.1001-3482.2015.04.015
1001-3482(2015)04-0061-05

