“认识概率”中的数学思想方法
钱娟
著名日本科学家米山国藏指出 “作为知识的数学,出校门不到两年可能就忘了,深深铭记在头脑中的唯有数学的精神、数学的思想研究方法和着眼点, 这些都随时随地发生动作,使人们终身受益”。数学的精髓不在于知识本身,而在于数学知识中所蕴含的数学思想方法。本文就“认识概率”这章中常用的一些基本的数学思想方法,作简单介绍,为后继进一步学习概率统计知识做好铺垫.
一、 “枚举思想”
枚举思想是解决概率问题的一个重要思想方法,对于一些简单的问题,通过枚举法即可获解.
例1(2014·浙江金华¬)一个布袋里面装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是【 】
【分析】:首先根据题意利用枚举法可得,摸出的球可能是红1,红2,红3,白1,白2,共五种情况所以是红球的的概率为 .
【答案】选A.
【点评】:本题中“袋中的五个球”被抽到的可能性相等,且该实验出现的结果为有限多个,从而应用“枚举思想”解决了本题,这两个特点也正是能运用枚举法求解的两个基本特征.另外,本题还巩固了简单概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .
二、 “方程思想”
方程思想是指解决数学问题时,先分学问题中的等量关系,设出未知数,建立方程或方程组,然后求解方程(组),使原问题获解.这一思想方法,在概率解题中应用广泛.
例2(2014·泰州)某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
【分析】(1)设该运动员共出手x个3分球,则3分球命中0.25x个,未投中0.75x个,根据“某篮球运动员去年共参加40场比赛,平均每场有12次3分球未投中”列出方程,解方程即可;
(2)根据概率的意义知某事件发生的概率,就是在大量重复试验的基础上事件发生的频率稳定到的某个值;由此加以理解即可.
三、“函数思想”
函数思想是指用函数的概念和性质去分析问题,转化问题和解决问题.
例3(改编) 已知一纸箱中装有5个只有颜色不同的球,其中2个白球,3个红球.
(1)求从箱中随机取出一个白球的概率是多少?
(2)若往装有5个球的原纸箱中,再放入 个白球和 个红球,从箱中随机取出一个白球的概率是 ,求 与 的函数解析式.
【分析】(1)从装有5个只有颜色不同球的纸箱中摸出一个球,共有3+2=5种不同的结果,其中摸到白球的结果有2个,所以取出一个白球的概率是 ;(2) 往装有5个球的原纸箱中,再放入 个白球和 个红球后,箱中共有球5+x+y(个),其中白球2+x(个),根据取出一个白球的概率是 列出关于x、y的方程,然后用含x的代数式表示y即可得到 与 的函数解析式.
【点评】 函数思想是一种重要的数学思想方法函数思想的实质是用联系和变化的观点提出数学对象,并抽象其数量特征,建立函数关系,运用函数的知识,使问题得到解决.这种思想方法在于揭示问题的数量关系的本质特征,重在对问题的变量进行动态研究,从运动变化
四 “数形结合的思想”
数学家华罗庚说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.“数”和“形”之间有着密切的联系,在一定条件下,可以相互转化,相互渗透.根据研究问题的需要,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,进而探求问题的解答的思想方法即数形结合的思想方法.本章中,利用表格、频率分布折线图、图形面积等探求概率的过程,便体现了“数形结合的思想方法”.
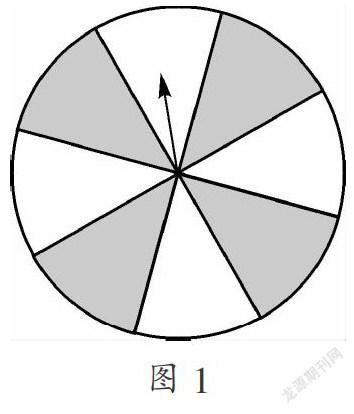
例4(2014·邵阳)有一个能自由转动的转盘如图,盘面被分成8个大小与性状都相同的扇形,颜色分为黑白两种,将指针的位置固定,让转盘自由转动,当它停止后,指针指向白色扇形的概率是 .
【分析】只要先弄清黑色区域面积和整个图形的面积关系即可.
【解答】根据题意,这个转盘是将“圆平均分成了8份”而制得,所以圆分得的8块图形的面积相等,故,黑色区域的面积是整个图形面积的一半.所以,转盘指向白色区域的可能性为 。
【点评】本题借助图形面积使问题获解,体现了数形结合的思想,同时本题中解答时也渗透了“整体的数学思想”.
五 “分类讨论的思想”
在解决一些稍复杂的概率问题,如问题中含有多种可能的情况时,往往需要考虑到各种情况对应的结果数,这就需要进行分类讨论.
(1)当a=-2时,求此不等式的解,并在数轴上表示此不等式的解集;
(2)小明准备了十张形状、大小完全相同的不透明卡片,上面分别写有整数-10、-9、-8、-7、-6、-5、-4、-3、-2、-1,将这10张卡片写有整数的一面向下放在桌面上.从中任意抽取一张,以卡片上的数作为不等式中的系数a,求使该不等式没有正整数解的概率.
- 初中生世界·八年级的其它文章
- “数”过三“关”
- 一路花开
- 同桌的你
- 张尧学 黄文婷 徐瑞
- 交流在美国
- 正确收集数据,科学分析数据

