基于金属密封的膨胀管悬挂力试验研究

杨晓莉（中国石油技术开发公司，北京100083）

·实验研究·

基于金属密封的膨胀管悬挂力试验研究

杨晓莉
（中国石油技术开发公司，北京100083）①

针对膨胀管胀后与套管结合效果差，悬挂能力弱等问题，提出了金属密封结构。在厚壁圆筒理论基础上推导了膨胀管悬挂力计算公式，利用ABAQUS模拟了膨胀管与套管在不同过盈量条件下膨胀力与悬挂力的变化规律，并进行试验验证。研究结果表明：胀后膨胀管与套管之间过盈量是悬挂力的决定因素；但是随着过盈量的增加，悬挂力的增幅与膨胀力的增幅并非正相关，因此有必要根据材料特性找到膨胀力与悬挂力相对最优的阀值；研究结果可以作为膨胀管现场施工设计的参考依据。

膨胀管；悬挂力；过盈量；试验

膨胀管技术是钻井工程领域的一项新兴技术［1-5］，被业界认为是21世纪钻井行业的核心技术之一。目前该技术广泛应用于套管补贴以及尾管悬挂等领域，表现出良好的发展前景。膨胀管沿径向发生塑性变形后通常不与套管直接接触，而是依靠硫化在管体表面韧性较好的橡胶悬挂在套管上。但是橡胶在高温高压环境，特别是膨胀管承受较大悬挂力条件下容易失效。因此有必要使用其他材料进行替代［6-7］。金属密封件能够有效提高膨胀管的耐温、耐压性能以及悬挂力，但是其韧性较差，在与套管发生贴合的过程中极易导致膨胀管压力上升，不利于安全作业。本文在厚壁圆筒理论基础上推导了膨胀管悬挂力计算公式，利用ABAQUS模拟了膨胀管与套管在不同过盈量条件下膨胀力与悬挂力的变化规律，最后进行了试验验证。

1　膨胀管悬挂力计算与ABAQUS分析

1.1 膨胀管悬挂力理论分析

由于胀后膨胀管与套管之间的贴合是依靠金属环与套管内壁的过盈配合实现，可以利用组合厚壁圆筒理论从过盈配合的角度对悬挂力进行分析［8-10］。图1为一厚壁圆筒，内径为a，外径为b，其中qa和qb分别为圆筒所受内压和外压，抽取半径为r、r＋d r的2个圆面和夹角为dθ的相邻径向面围成的单元体cdef，单元体放大图如图1。由于变形相对于轴线对称，所以各点径向位移只与半径r有关。变形后单元体cf边移到cf，de边移到d′e′，周向应变为

c点径向应变为：

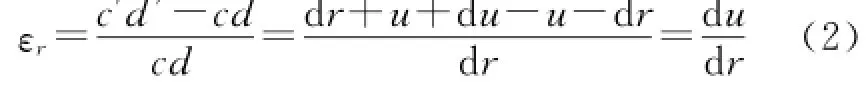
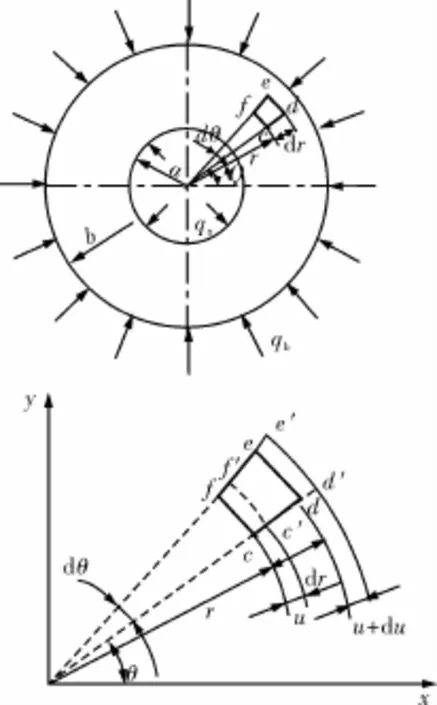
图1　金属环应力应变状态

图2为单元体应力状态图。其中σr、σθ分别为单元体径向和周向应力，只与半径r有关，且两个周向应力相等，cf面上的正应力为σr，de面上的正应力为（σr＋dσr），无剪应力，将作用于单元体上的内力投影于坐标r，得：

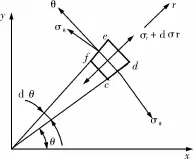
图2　单元体受力状态

根据广义虎克定律，可以得位移通解：

式中：A，B为系数。

将式（4）代入式（3）可得应力表达式：式中：E为膨胀管材料弹性模量。

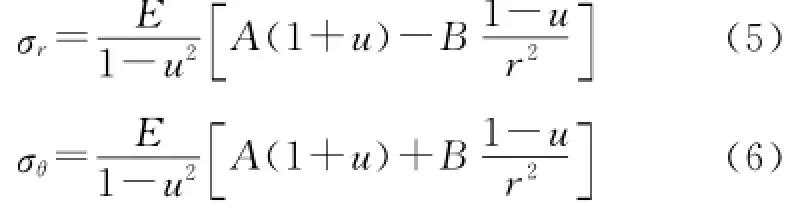
确定积分常数的边界条件，即r＝a时，σr＝－qa，r＝b时，σr＝－qb，可得应力表达式如下：

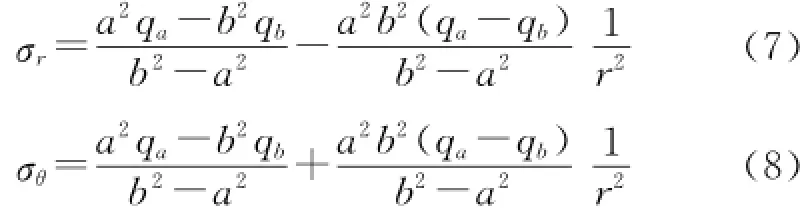
最终可得配合压力表达式：悬挂力表达式：

式中：r为配合公称半径；l为配合长度；f为摩擦因数；ui为单元体cf的径向位移；ue为单元体de的径向位移；δ为变形之后膨胀管与套管之间过盈量。

1．2 有限元数值模拟

由于本文所研究的对象是多非线性问题，即：状态非线性的接触问题、结构非线性的大变形问题、材料非线性的弹塑性问题。因此可以选用ABAQUS作为仿真分析软件研究膨胀管膨胀过程应力变化以及胀后悬挂力。膨胀管与膨胀锥的几何及力学参数如表1～2所示。金属环与膨胀管材料相同。

膨胀过程实际工作情况较为复杂，现简化如下：

1） 膨胀尾管约束上端所有节点自由度。

2） 膨胀锥头约束z向和x向自由度，对其施加沿y轴负向的恒定速度，当膨胀结束后，膨胀锥头停止运动。

3） 外层套管上端固定所有自由度，膨胀结束后开放y向自由度，并对其施加推力，推力大小与时间成正比。

4） 金属与金属之间的摩擦因数为0．1。

表1　膨胀管规格及模型长度

表2　膨胀管材料及力学性能

膨胀过程起始阶段，膨胀管与外层套管上端固定，给膨胀锥头施加恒定速度使之沿轴向向下匀速移动，当膨胀结束后，开放外层套管自由度并对其施加轴向推力，当推力增大到临界数值时膨胀尾管与外层套管分离，认定此临界数值为膨胀管与套管之间的悬挂力。膨胀过程如图3所示

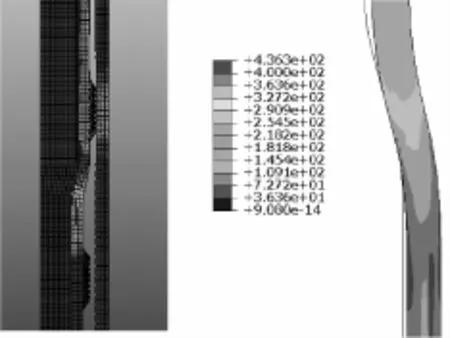
图3　有限元ABAQUS模拟

本文模拟了胀后膨胀管金属环与套管之间不同过盈量条件下的膨胀力，悬挂力的变化情况，考虑到膨胀力的因素，选择过盈量在1．2～1．5mm。结果表明随着过盈量的增加，膨胀力明显变大，且呈线性增长；膨胀管与套管之间悬挂力也有一定增加，但是增加幅度远小于膨胀力，因此有必要根据材料特性找到膨胀力与悬挂力相对最优的阀值，通过对比发现，当过盈量1．4mm时，膨胀力峰值181 k N，悬挂力450 k N，单位膨胀力获得的悬挂力最大。膨胀力与悬挂力变形如图4～5所示。

图4　不同过盈量的膨胀力变化

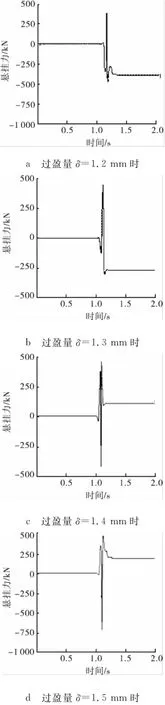
图5　不同过盈量的悬挂力变化

2　试验与讨论

为验证理论研究的科学性，本文设计膨胀管膨胀试验与悬挂力测试试验，试验用膨胀管、膨胀锥、套管等部件的几何尺寸、力学性能与模拟试验材料参数基本一致。金属环宽度10mm，胀后与套管设计过盈量在1．2～1．5mm，试验用材料及设备如图6所示。

图6　试验用材料及设备

试验过程中，膨胀管膨胀顺利，不同过盈量条件下的膨胀力峰值有明显不同，增加幅度逐渐变小，这主要是由于金属环受双向挤压，过盈量增加会导致金属环塑性变形变大，需要更多做功，考虑材料尺寸误差，膨胀力变化并不为线性；膨胀后在试验机进行了膨胀管与套管的脱挂试验，从获取的数据可以看出，悬挂力在一定范围的过盈量条件下变化差别不大。这主要是由于膨胀管胀后会出现回弹现象，导致金属环与套管之间接触力发生变化。如图7所示。

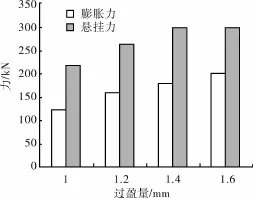
图7　试验过程膨胀力与悬挂力变化

由于试验材料尺寸偏差，试验结果与计算值，模拟值有一定差异，但是反映出相同的变化规律。因此有必要根据金属环材料特性条件，选择合适的过盈量，以保证使膨胀力与悬挂力达到最优。

3　结论

1） 通过理论与试验方法研究了膨胀管胀后与套管之间的悬挂力。研究结果表明，随着过盈量的增加，悬挂力的增幅与膨胀力的增幅并非正相关；在安全作业范围内膨胀力与悬挂力之间存在相对最优阀值，该阀值由密封件材料特性决定；以金属铜为密封件，当过盈量为1．4mm时单位膨胀力获得最大悬挂力。

2） 在厚壁圆筒理论基础上推导的膨胀管悬挂力计算结果以及ABAQUS模拟研究与试验结论有较高的一致性，研究结果可作为膨胀管现场施工的参考依据。

3） 膨胀管材料特性与密封件结构存在巨大的改进空间，是今后的研究方向。

［1］ 沙庆云，任毅．石油专用管材生产技术的现状及进展［J］．鞍钢技术，2000（6）：13-15．

［2］ 李作会．膨胀管关键技术研究及首次应用［J］．石油钻采工艺，2004，26（3）：17-19．

［3］ 关大新，杨文晨．特殊抠油井管的发展［J］．天津冶金，2001（增刊）：20-23．

［4］ 高连新，史交齐．油套管特殊螺纹接头连接技术的研究现状及展望［J］．石油矿场机械，2008，37（2）：15-19．

［5］ Stewart R B Shell．Expandable tubulars promise to cut costs while increasing step out and well depths［G］．DRILING CONTRACTOR，November／ December 1998：37-39．

［6］ 杨明．可膨胀管明显提高钻井效率［J］．世界石油工业，2000：7（3）：35-37．

［7］ 王俊芳，曹鸿斌，孙朝林，等．国外套管钻井技术综述［J］．断块油气田．2001，8（6）：67-68．

［8］ 徐宜山．胀管技术简介［J］．科学与财富，2010（6）：22-23．

［9］ 张建兵，施太和，练章华．钻井实体膨胀管技术［J］．石油机械，2003，31（增刊）：128-131．

［10］ 韩伟业，裴晓含，李益良，等．膨胀管抗外挤强度试验研究［J］．石油矿场机械，2014，43（5）：56-59．

Experimental Study of Hanging Force of Solid Expandable Tubular Based on Metal Seal

YANG Xiaoli
（China Petroleum Technology and Development Company，Beijing 100083，China）

The post expanded tubular was usually integrated with casing not very solid because of environmental issues，in an effort to address it themetal seal structure was raised to enhance the hanging force，the formula calculating the hanging force was deduced and the ABAQUS was em-ployed to simulate the change of hanging force in relation with the interferencemagnitude，finally the experiments were carried out to testify the approach．The results demonstrated that the inter-ference between the casing and post expanded tubular was the decisive factor of the hanging force，but it was not linearly related as the interference increased，therefore the valve value based on thematerial charactermust be found to optimize the relation between the expanding force and the hanging force，ensuring the safe operation and the desired hanging force．The results could be served as reference in the field operation．

solid expandable tubular；hanging force；interference；experiments

TE925．207

A

10．3969／j．issn．1001-3842．2015．08．010

1001－3482（2015）08－0044－05

①2015－01－04

杨晓莉（1981-），女，山东人，2003年毕业于天津大学机械工程学院，主要从事石油物资装备出口管理，Email：euphoria1934＠aliyun．com。