模型思想在小学数学教学中的应用
邱廷建
《数学课程标准》(2011年版)提出:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果,并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想,提高数学学习的兴趣和应用意识。”
模型思想是《数学课程标准》(2011年版)新增加的核心概念,作为一种基本的数学思想提出来,这就需要教师对模型思想的含义及要求有准确理解和把握,并把要求落实到数学课堂教学中。在小学阶段,小学生对数学模型思想的感悟、体会和建立,不像某些数学知识的掌握那样可以立竿见影,需要教师在小学数学教学中,逐步渗透和引导学生不断感悟,让学生经历数学建模过程,不断感悟数学模型思想,通过建立数学模型来解决实际问题。
一、准确理解,弄清模型思想的含义及要求
东北师大史宁中教授在《数学思想概论》中指出:“数学发展所依赖的思想在本质上有三个:抽象、推理、模型……通过抽象,在现实生活中得到数学的概念和运算法则,通过推理得到数学的发展,然后通过模型建立数学与外部世界的联系。”从数学产生、数学内部发展、数学外部关联三个维度概括了对数学发展影响最大的三个重要思想。这说明模型思想是数学的基本思想之一。
作为中小学数学课程中的模型思想,应该在数学的本质意义上让学生去感悟,去体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,去体会和理解数学与外部世界的联系,并让学生在头脑中建立起这样的认识:数学与外部世界不是分离的而是紧密联系的,连接它们之间的“桥梁”就是数学模型。
模型思想在中小学数学教学中的渗透和应用,就是要引导学生经历数学建模的过程,让学生感悟模型思想。也就是说,模型思想的建立要蕴含于数学建模之中。所谓数学模型,就是根据特定的研究目的,采用形式化的数学语言,抽象、概括地表征所研究对象(中小学主要指现实问题)的主要特征、关系所形成的一种数学结构。在义务教育阶段的数学课程中,为表征特定的现实问题,用字母、数字及其他数学符号建立起来的代数式、关系式、方程、函数、不等式,及各种图表、图形等都是数学模型。一般来说,建立数学模型的过程应包括“观察实际情境—发现、提出问题—抽象成数学模型—得到数学结果—检验并调整、矫正模型”等多个环节。但是,义务教育阶段特别是小学阶段的数学建模应视具体的课程内容要求而定,不一定要经历所有环节。《数学课程标准》(2011年版)将前面多个环节的建模过程进一步简化为下面三个环节:首先,从现实生活或具体情境中抽象出数学问题。发现和提出问题是数学建模的起点,然后用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律。在这个环节中,学生要通过观察、分析、抽象、概括、选择、判断等数学活动,完成模式抽象,建立数学模型。这是建模最重要的一个环节。最后,通过模型求出结果并讨论结果的意义。这样,学生在经历数学建模的过程中,不仅理解和掌握了知识技能,而且感悟和体会了模型思想,还积累了数学活动经验,其情感态度与价值观也得到了发展。
二、注重建构,引导学生经历数学建模的过程
《数学课程标准》(2011年版)指出:“在呈现作为知识和技能的数学结果的同时,重视学生已有的经验,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程。”根据建模过程简化后的三个环节,可引导学生经历“问题情境—建立模型—求解验证”的数学建模过程,引导学生主动建构。学生在经历数学建模的过程中,理解和掌握有关知识技能,积累数学活动经验,感悟模型思想的本质,提高发现问题、提出问题、分析问题和解决问题的能力。下面以“平行四边形的面积”的教学为例,说明建立一个数学模型的过程。
1.创设情境,提出问题
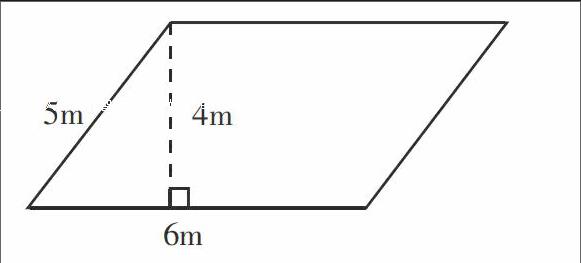
在提出问题、确定研究模型环节,教师应尽可能为学生提供真实的问题情境,使学生产生学习需要。问题可以由教师直接提出,也可以通过创设情境让学生提出,但要注意找准学生认知的最近发展区,使提出的数学问题能引发学生的思考。例如,可出示一个平行四边形花坛的情境图(如下),问:这个平行四边形花坛的面积是多少?这里提出的探究问题是如何计算平行四边形的面积,也就是需要建立平行四边形面积计算的数学模型。
[5m][4m][6m]
2.猜想与验证,建立模型
在数学抽象、建立模型环节,教师要引导学生针对问题特点和建模目的作出合理猜想,并验证猜想。这个环节教师不应过早地对学生的猜想进行评判,而应重点关注猜想背后的思想,关注学生是否调动了原有的知识经验,并引导学生在操作、证明、交流和质疑中用事实验证自己的猜想,或纠正自己的错误猜想。例如,怎样计算这个平行四边形花坛的面积?如果学生猜想“5×4”(邻边×高),教师就应引导学生质疑:“邻边×高”究竟对不对?怎样证明这一猜想是否正确?然后教师利用课件动态演示,用正方形面积单位测量,采用数方格的方法验证猜想。通过测量可以知道,用“5×4=20”个面积单位铺这个平行四边形,没有铺满,因此,用“邻边×高”计算平行四边形的面积是错误的。如果学生猜想“6×5”(底边×邻边),教师继续利用课件动态演示,用面积单位测量,采用数方格的方法验证猜想。通过测量可以知道,用“7×4=28”个面积单位铺这个平行四边形,就已经超出4个面积单位,如果用“6×5=30”个面积单位铺这个平行四边形,就会超出更多的面积单位,因此,用“底边×邻边”计算平行四边形的面积是错误的。同样,如果学生猜想“6×4”(底边×高),教师再次利用课件动态演示,引导学生用面积单位测量,采用数方格的方法验证猜想。通过测量可以知道,用“6×4=24”个面积单位铺这个平行四边形,正好铺满。因此,用“底边×高”计算平行四边形的面积是正确的。为了进一步证明“平行四边形的面积=底边×高”具有普遍性,教师还可以渗透转化思想,继续引导学生用“剪拼法”证明。通过验证活动,学生就能发现,用“邻边×高”或“底边×邻边”计算平行四边形的面积的猜想都是错误的,正确的数学模型应该是“平行四边形的面积=底边×高”,用字母表示是:S=a×h。这个过程,引导学生猜想、测量和比较,验证猜想,将错误的猜想逐一排除,让学生感知、体会到“在猜想中排除”的学习方法,学生对这样建立起来的正确的数学模型,印象是深刻的。
3.应用模型,解决问题
建立数学模型,只是一种手段而不是目的。因为从实际问题出发建立的数学模型,还要运用已有的数学方法来进行分析、计算和推导,进而获得数学上的解,然后用这个数学上的解为解决实际问题进行科学解释,形成新的理论和作出新的预见。因此,在应用模型、解决问题这个环节,教师既要引导学生应用建立的数学模型解决实际问题,也要对解决的实际问题进行科学解释。例如,建立了“S=ah”的数学模型后,可以让学生完成课始提出的问题:“一个平行四边形花坛的底是6m,高是4m,它的面积是多少?”把实际问题中的数据代入关系式,进行运算:S=ah=6×4=24(平方米)。为了加深学生对“S=ah”这个数学模型的理解,还需要进一步向学生解释、说明,平行四边形面积计算公式中的“底”与“高”必须相互对应,如果不对应,那么“底”与“高”的乘积就不是这个平行四边形的面积。因此在应用模型的过程中,教师还要注意不能让学生简单地套用模型,而应该引导学生展示解决问题的思维过程,并对思维过程进行剖析,进一步加深学生对数学模型的理解,促进数学模型的内化。
三、重视渗透,引导学生感悟模型思想
《数学课程标准》(2011年版)指出:“数学思想蕴含在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括……学生在积极参与教学活动的过程中,通过独立思考、合作交流,逐步感悟数学思想。”学生对模型思想的感悟需要经历一个过程,在这个过程中,学生总是从相对简单到相对复杂,相对具体到相对抽象,逐步积累经验,初步掌握一些建模方法,逐步形成运用模型进行数学思维的习惯。因此在小学数学教学中,教师要注意根据学生的年龄特征和不同学段的要求,循序渐进地逐步渗透模型思想,将模型思想的渗透和感悟蕴含于数学概念、计算公式、运算定律、运算法则和解决问题的教学中。
1.在数学规律性知识的教学中渗透和感悟模型思想
小学数学知识的分类,从知识方面考虑,一般可以分为概念性知识、规律性知识和技能性知识。如各种运算定律(加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律)以及几何求周长、面积和体积的计算公式等,都属于规律性知识。在这些规律性知识的结论中,往往涉及一个简单的数学模型,这需要教师在教学中逐步渗透模型思想,并引导学生感悟模型思想。
例如“乘法分配律”的教学,首先要通过创设情境提出问题:3×(5+8)是不是等于3×5+3×8?这种情况对其他这类算式是否都成立?其次,让学生通过观察,验证下面的式子:6×(9+11)=6×9+6×11,8×(32+68)=8×32+8×68……学生通过观察、比较、验证,就会找出其中的关系,并用字母表示出来:(a+b)×c=a×c+b×c。最后,解决问题并推广。当a=4,b=7,c=2时,2×(4+7)=2×4+2×7。对于任意数a、b、c,上述关系总是成立的。这样,教师引导学生建立乘法分配律的数学模型,并把已建立的数学模型推广到一般情况,实际上就渗透了模型思想,让学生感悟得出的结果:(a+b)×c=a×c+b×c,不只局限于一道或几道具体的题目,而是a、b、c可以代表任意数。由于数学模型具有抽象概括的功能,学生如果能从普遍意义上去理解数学模型,就能有效掌握相应的规律性知识。
2.在解决问题的教学中渗透和感悟模型思想
解决问题的过程,实际上是对实际问题进行数学抽象,并建立数学模型的过程。在解决问题的教学中渗透和感悟数学模型思想,教师既要重视引导学生提出问题并用数学语言表达,又要重视引导学生分析数量关系并进行数学抽象,注重用数学符号把实际问题中的数量关系表达出来,还要重视引导学生列式解答并优化解答方案,使问题得到解决并推广。
例如,“用反比例解决问题”的教学,可出示这样一道题:“学校小商店有两种圆珠笔。小华带的钱刚好可以买4支单价1.5元的,如果他想都买单价是2元的,可以买多少支?”首先,教师提出问题:题中有哪两种相关联的量?它们是不是成比例的量?成什么比例?为什么?其次,分析数量关系并建立公式。单价和数量是两种相关联的量,它们与总价有下面的关系:单价×数量=总价。因为总价一定,也就是单价和数量的乘积一定,所以单价和数量成反比例。最后,解决问题并推广。解:设可以买x支,根据单价和数量成反比例关系,列出方程:2x=1.5×4,求出方程的解:x=3。在此基础上,还要引导学生将反比例关系用字母表示出来:x×y=k(一定),让学生感悟x和y可以表示任意两种相关联的量,只要它们的乘积(k)一定,这两种相关联的量就成反比例关系。这样旨在进一步渗透反比例函数思想,帮助学生建立数学模型。
在解决问题的教学中渗透和感悟数学模型思想,可以使学生更清晰地理解应用问题中的数量关系,更好地掌握应用问题的结构特征,更有效地发展学生的抽象概括能力。需要注意的是,不能让学生在没有理解的基础上死套公式,按部就班,要防止学生形成机械学习的不良学习习惯。
总之,在小学数学教学中,教师要重视模型思想的应用,既要让学生经历和体验数学建模的过程,也要让学生感悟和应用模型思想,还要引导学生回顾和反思数学建模的过程。在教学中,通过逐步渗透和引导学生感悟、反思模型思想,调动学生建模的兴趣,总结建模经验,体会模型力量,感悟模型魅力,从而形成模型思想,逐步提高学生运用数学模型解决实际问题的能力。

