炉膛压力管道微弱泄漏信号检测方法研究
安连锁,冯 强,沈国清,姜根山,张世平,王 鹏,周 鑫
(1.华北电力大学电站设备状态监测与控制教育部重点实验室,北京102206;2.北京电力经济技术研究院,北京100055)
锅炉压力管道泄漏直接影响热力发电站的安全经济运行,对压力管道初期泄漏进行及时检测能够降低运行事故概率,并带来一定的经济性.采用声学法检测泄漏信号虽然具有安装和维护方便、非接触式测量、实时性以及不需要外加能量等优点,被广泛应用于电站锅炉、石油和天然气检查等方面,但是对于电站锅炉炉膛复杂的声环境,泄漏信号衰减较大,通过声压和频谱分析很难检测到初期的泄漏信号,且仅通过声压和频谱分析检测泄漏信号很容易造成误判和漏判.若在早期发现电站锅炉压力管道泄漏,可及时上报,给电网调控预留出足够时间,合理安排停炉.
经验模态分解(Empirical Mode Decomposition,EMD)[1-2]可对信号进行平稳化处理,并具有自适应的优点,能够将信号分解为若干本征模态函数(Intrinsic Mode Function,IMF).对包含特征信号的IMF进行研究能够达到一定的降噪效果.在微弱信号检测方面,由于Duffing振子对噪声具有较显著的免疫力,并且其对有用信号敏感的特性被广泛应用于各领域.针对炉膛压力管道初始微弱信号检测问题,采用EMD 联合自相关差分Duffing振子(CD-EMD)方法进行了研究.
1 经验模态分解
美国NASA 的Nordon E Huang 工作组于1998年提出EMD 方法[3].该方法能够将任意信号分解为若干IMF和一个残余项,因为依据自身时间尺度特征进行信号分解,所以不必像小波处理一样预先设置基函数.在对信号进行平稳化处理的过程中,根据待检测信号的特征,选取适当的IMF 能够达到降噪的效果.从本质上说,EMD 方法将时域信号按照频率尺度逐级分解,产生若干IMF.
采用EMD 方法将信号分解为IMF 时需要满足2个条件:一是对于整个数据序列,存在相等或者至多差1的极值点个数和过零点个数;二是对于任意一点,信号局部极大值和局部极小值所定义的上包络线和下包络线的均值为0.
在满足上述条件的前提下,EMD 方法可将信号x(t)筛选为若干IMF和一个残余项,具体步骤如下:
(1)确定数据序列的所有极大值点,利用三次样条插值拟合出上包络线u(t),采取同样方法对所有极小值点拟合出下包络线d(t),并记上包络线和下包络线的均值为m(t),即m(t)=[d(t)+u(t)]/2.
(2)定义h1(t)=x(t)-m(t),对于非线性信号和非平稳信号,通常h1(t)不满足IMF 所要求的2个条件,对于不满足条件的h1(t)需要重复执行步骤(1)和步骤(2),直至h1(t)符合IMF 所要求的条件为止,将满足条件的h1(t)记作h1imf(t).
(3)将原数据序列减去h1imf(t),得到剩余数据序列r1(t):

(4)将剩余数据序列r1(t)作为原始数据序列,重复步骤(1)~步骤(3),依次分解得到:

筛选过程的停止准则[4]为:限制两连续处理结果的标准差Sd,通常Sd的取值为0.2~0.3.Sd的表达式如下:

式中:T为数据序列时间尺度;hi(k-1)(t)和hik(t)为IMF筛选过程中两连续处理结果的数据序列;k为第i个IMF筛选过程中的次数序列.
信号经过上述步骤被分解为n个IMFhiimf(t)和一个残余函数rn(t),即
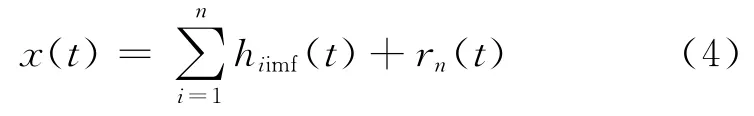
其中,各IMF分量包含了不同时间尺度的特征信号,残余函数表示了原数据趋势量信息,如图1所示.

图1 电站锅炉实测噪声信号的EMD方法分解示意图Fig.1 EMD method diagram of background noise in power plant boiler
2 基于自相关及时间尺度的差分Duffing振子检测系统
2.1 基于时间尺度的Duffing振子动力学模型
Holmes型Duffing系统方程为

式中:k为阻尼系数;fcos(ωt)为周期项;-x+x3为非线性项,非线性项部分决定了Duffing振子具有非线性动力学特性.
先前的学者在研究Duffing振子时通常采用小频率参数来检测低频信号.当检测高频信号时需要增大阻尼系数k,并且同时调整周期项系数f,然而实际运用中k应取较小值,因为当k较大时,含噪声待检测信号输入Duffing振子不足以使系统状态跃变,即不存在混沌状态到大尺度周期状态的相变[5].对于不同的待检测信号,需要根据大量实验数据调整临界参数k和f,其过程较为繁琐.针对上述问题,采用赖志慧等[6]提出的变尺度检测方法,该方法对任意频率的信号在时间尺度上进行变换,然后将变换后的信号输入到Duffing振子,其核心在于将任意频率的信号转换为角频率为1rad/s的信号.
构造Duffing振子检测系统:

式中:Ⅰ(t)为输入信号,包含了待检测周期信号Acos(ωt)和噪声n(t),即Ⅰ(t)=Acos(ωt)+n(t).
由于Duffing振子对噪声具有免疫特性[7],因此对于不含待检测信号的噪声,系统不会发生状态跃变,仍处于混沌状态,但当输入信号含有微小幅值的待检测信号时,系统会发生状态跃变,进入大尺度周期状态,如图2所示.对于电站锅炉压力管道的微弱泄漏信号,正是应用Duffing振子对特定频率信号的敏感性来检测的.
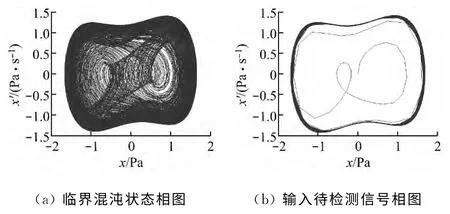
图2 Duffing振子检测系统相变图Fig.2 Phase diagram of Duffing oscillator detection system
在上述分析中,将待检测信号初始相位均假设为0,然而实际工程应用中,初始相位为0的情况几乎不存在.由文献[6]可知,由于待检测信号初始相位的不同而存在一定的检测误区,使得Duffing振子微弱泄漏信号检测在工程应用中受到限制.
2.2 基于自相关的差分Duffing振子
差分法采用的是双振子模式,构造方程如下:
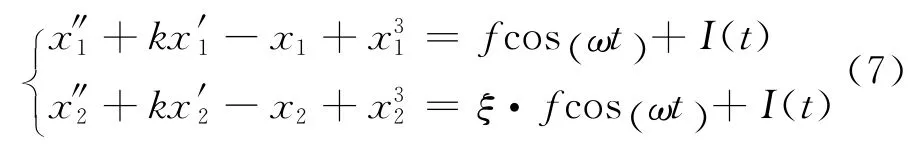
式中:Ⅰ(t)=Acos(ωt+φ)+n(t),φ∈[0,2π];ξ通常为1~1.5内的数值,若ξ=1,则式(7)等同于一维Duffing振子.
ξ决定了差分后共模成分和混沌成分的凸显,当其值趋于1时,两振子差分后共模噪声得到抑制,但经验阈值越小,影响混沌状态判别的准确度;而当其值趋于1.5时,经验阈值增大,Duffing振子输出相位差增大,分析难度增加,在本文中ξ取1.004.
对Ⅰ(t)进行自相关运算,则
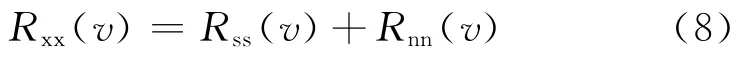
式中:v为自相关时延值;R为自相关输出值;下标xx表示实际接受信号,ss表示纯信号,nn表示噪声信号.
对于炉膛背景噪声n(t),若v较大,Rxx(v)表现为Rss(v)特征.那么对于待检测信号Acos(ωt+φ),则有
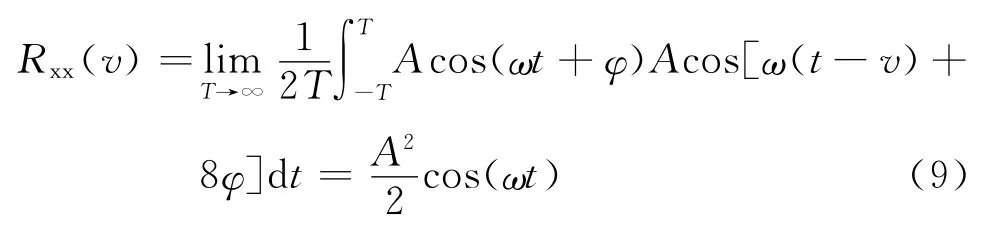
通过式(9)可知,输入信号经过自相关运算后,可消除待检测信号相位差时干扰.
3 小波变换
小波理论是在傅里叶变换基础上发展而来的,由于其对时域及频域都具有局部特征表征能力,因此广泛应用于各个行业[8-9].进行小波变换时首先要选取小波函数,小波函数必须满足:
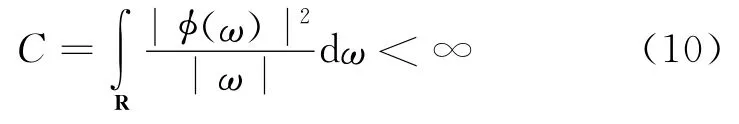
式中:φ(ω)为φ(t)的傅里叶变换,且φ(ω)∈L2(R),φ(ω)ω=0=0;L2(R)表示二次可积函数组成的空间,φ(t)为小波基函数.
对小波基函数进行伸缩、平移,可以得到小波基函数φa,τ(t):

式中:a为尺度因子,a∈R,a>0;τ为平移因子,τ∈R.
实际工程应用中采集到的均为离散信号,需要进行尺度因子和平移因子的二进制变换,取a=2i,τ=2ij,j∈Z,带入式(11),对应的离散小波基函数为
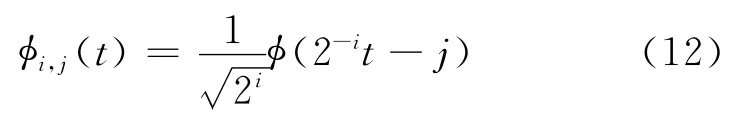
对于任意L2(R)空间,在小波基函数φa,τ(t)下展开函数f(t),称为函数f(t)的连续小波变换,其表达式为
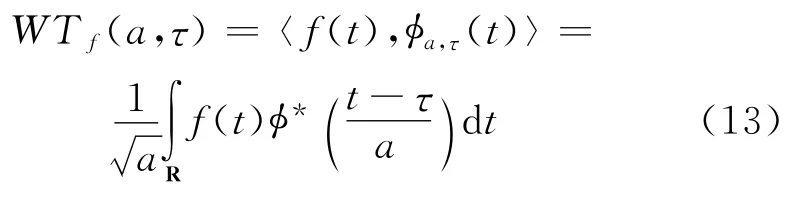
式中:φ*((t-τ)/a)为φ((t-τ)/a)的共轭复数.
函数f(t)经过连续小波变换后,可由下式重构恢复原信号,即进行小波逆变换:
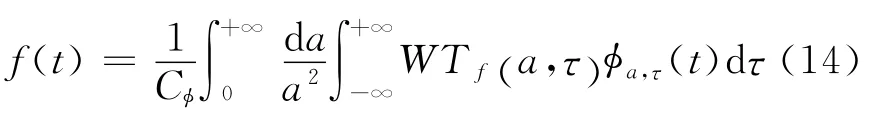
式中:Cφ为小波基函数φa,τ(t)的可容许条件.
4 炉膛压力管道微弱泄漏信号检测系统
电站锅炉压力管道微弱泄漏信号检测系统由声感知设备、声波导管、信号调理器和功率放大器等设备组成,其中声波导管起到隔离燃烧和隔热的作用,对声感知设备起到保护作用.声感知设备的布置方式需要结合炉膛复杂的实际环境进行调整,在此不讨论,仅给出一般性示例,如图3所示.
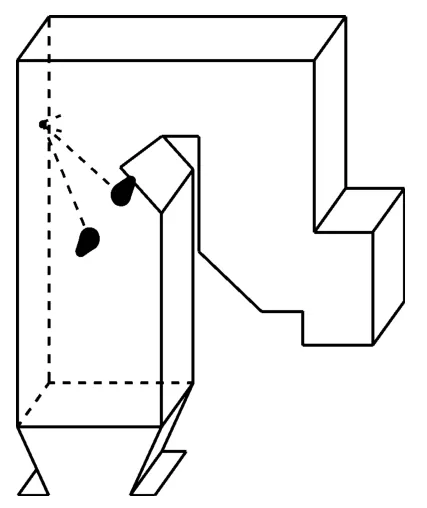
图3 电站锅炉立体图Fig.3 Power plant boiler stereogram
声感知设备设定为每隔一段时间采集一次,并将采集数据与先前一次的采集数据进行分析对比.对采集到的数据先进行EMD 分解,对包含泄漏信号特征量的IMF进行频谱分析,同时将对应的IMF经自相关处理后输入至差分Duffing 振子检测系统,通过经验阈值进行微弱泄漏信号判别.
5 仿真结果及分析
为评估EMD、小波、EMD 联合Duffing 振子(D-EMD)和CD-EMD 方法的性能,在待检测信号中加入现场采集的炉膛背景噪声,炉膛背景噪声采样频率设定为102 400Hz,采样个数为65 536.采用不同信噪比对各方法分别进行信号检测仿真实验.信噪比计算公式采用,其中为待检测信号的均方值,为噪声信号的均方值.
为了从时域及频域图上显示各方法检测效果,待检测声源选取0.6 MPa间歇射流气动声源(以下简称0.6 MPa气动声源).由于高频信号在炉膛实际高温粉尘环境中衰减较严重,因此选取10kHz以下的4个峰值频率(2 583Hz、3 588Hz、6 309Hz和9 152Hz)为信号特征频率,如图4所示.

图4 0.6 MPa气动声源频谱图Fig.4 Frequency spectrum of the 0.6 MPa pneumatic sound
5.1 EMD方法与小波分解效果对比研究
将0.6 MPa气动声源信号加入炉膛背景噪声,当信噪比为-5dB 时,从时域图上EMD 方法和小波分解均能较好地辨别气动声源信号,但实际泄漏信号为非间歇射流模型,因此在时域图上进行判别存在技术难题.在频域方面,EMD 方法可以较好地检测到信号特征频率,如图5所示(其中FFT 表示傅里叶变换).小波分解采用db5小波基进行5层分解,能够检测到2 583Hz、3 588Hz和6 309 Hz频率,但出现主峰值7 645 Hz频率干扰,且无法有效检测到9 152Hz频率,如图6所示.

图5 信噪比为-5dB时EMD方法分解高频重构时域图及对应的FFT 频谱图Fig.5 High-frequency reconstruction time domain and FFT frequency domain by EMD method at-5dB signal to noise ratio
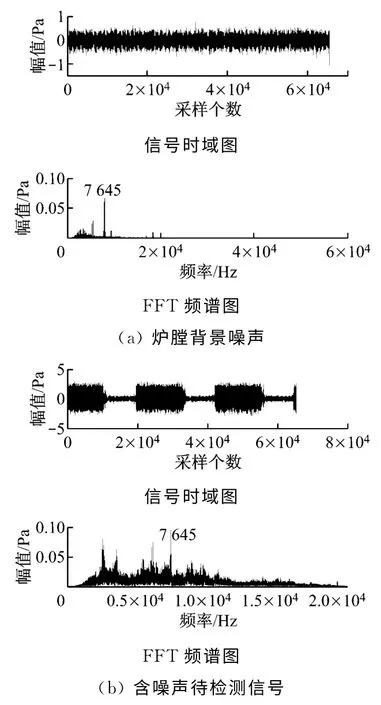
图6 信噪比为-5dB时小波分解高频重构时域图及对应的FFT 频谱图Fig.6 high-frequency reconstruction time domain and FFT frequency domain by wavelet decomposition at-5dB signal to noise ratio
当信噪比为-14.5dB 时,在时域方面,EMD方法及小波分解均能较好地辨别气动声源信号;在频域方面,EMD 方法分解后的峰值频率仍为特征频率,但出现旁瓣干扰,如图7所示.小波分解出现严重的主频干扰,且2 583Hz畸变为2 547Hz,如图8所示,因此在-14.5dB信噪比环境下,小波分解不适用于炉膛压力管道微弱泄漏信号检测.

图7 信噪比为-14.5dB时EMD方法分解高频重构时域图及对应的FFT 频域图Fig.7 High-frequency reconstruction time domain and FFT frequency domain by EMD method at-14.5dB signal to noise ratio
5.2 D-EMD与CD-EMD方法效果对比研究
当信噪比为-24dB时,EMD 方法分解已无法正常识别特征频率,如图9所示,因此引入D-EMD方法,并改进为CD-EMD 方法,将2种方法进行对比分析.在无初始相位干扰情况下,信噪比为-24 dB时,D-EMD 和CD-EMD方法的输出相图为大尺度周期状态,如图10和图11所示.

图8 信噪比为-14.5dB时小波分解含噪声待检测信号时域图及FFT 频谱图Fig.8 Time domain and frequency domain of noisy signals by wavelet decomposition at-14.5dB signal to noise ratio

图9 信噪比为-24dB时EMD方法分解含噪声待检测信号时域图及FFT 频谱图Fig.9 Time domain and frequency domain of noisy signals by EMD method at-24dB signal to noise ratio

图10 D-EMD方法输出相图Fig.10 D-EMD method output phase diagram

图11 CD-EMD方法输出相图Fig.11 CD-EMD method output phase diagram
5.2.1 初始相位的干扰
根据文献[8]的结论,当φ∈[0,π/3]∪[5π/3,2π]时,Duffing振子可以对微弱周期信号进行有效识别,因此选取不同待检测信号初始相位(π/6、5π/6、7π/6 和11π/6),分别采用D-EMD 和CD-EMD方法进行仿真实验.
图12和图13分别给出了D-EMD 和CD-EMD方法不同初始相位的输出相图.表1给出了2种方法不同初始相位状态的对比.由图12、图13和表1可以看出,D-EMD 方法受待检测信号初始相位的干扰严重,容易出现误判;而CD-EMD方法通过引入自相关方法,能够将任意初始相位待检测信号转换为0相位,避免了初始相位的干扰,消除了由初始相位导致的特征频率误判.

图12 D-EMD方法不同初始相位的输出相图Fig.12 Output phase diagram of D-EMD method with different initial phases
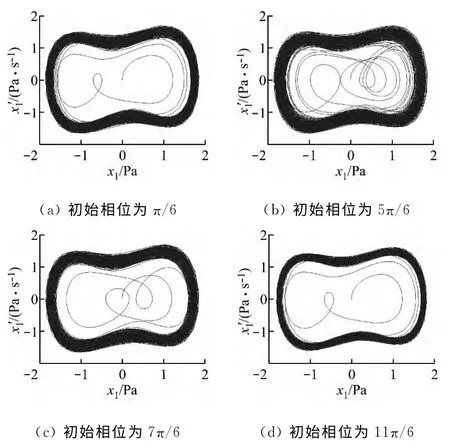
图13 CD-EMD方法不同初始相位的输出相图Fig.13 Output phase diagram of CD-EMD method with different initial phases

表1 初始相位的影响对比Tab.1 Comparison of influence among different initial phases
5.2.2 CD-EMD方法特征频率的判别
CD-EMD 方法对于混沌状态判别的优点在于可以通过设定经验阈值进行判别,而且有效地避开了lyapunov等数值计算方法,提高了运算效率,增强了系统运行的实时性.当输入信号不包含特征频率时,差分波形图如图14(a)所示,幅值在2.5Pa以上;当输入信号包含特征频率时,差分波形图如图14(b)所示,幅值在0.1Pa以下.在实际工程应用时可以通过设定经验阈值的方式,当差分幅值高于经验阈值时即为混沌状态,输入信号不包含特征频率;当差分幅值低于经验阈值时即为大尺度周期状态,输入信号包含特征频率,若多个CD-EMD阵列同时检测到特征频率,即可判定炉膛压力管道出现微弱泄漏信号.
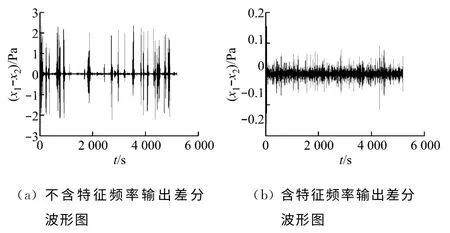
图14 差分波形图Fig.14 Difference waveform
5.2.3 实际运行中特征频率的选取
本研究针对泄漏初期微弱泄漏信号,高频泄漏信号在原始未经处理的频谱图上难以识别,而经EMD 方法分解后,炉膛背景噪声也存在少量高频信号,但是总体上与泄漏信号存在差别.
对1mm、2mm、3mm、5mm 和9mm 口径的喷嘴在8个大气压下使用空气压缩机模拟泄漏信号,采用前文提到的控制信噪比的方式,使信噪比为-24dB,将不同口径的泄漏信号加入炉膛背景噪声,EMD 方法分解结果如图15所示.
对比各口径喷嘴EMD 方法分解输出的2imf图形可知,炉膛背景噪声输出图形在主峰值右侧频率,频率分布骤降,总体分布呈三角分布形式;含噪声待检测信号输出图形在主峰值右侧频率,频率有一段平坦部分,总体分布为梯形分布.判别泄漏信号特征频率从主峰值右侧频率分布入手,从主峰值右侧寻几组次峰值(以下简称右次峰值),列出差分Duffing振子阵列,炉膛背景噪声右次峰值不足以驱动差分Duffing振子,而含噪声待检测信号能够驱动差分Duffing振子发生相变.

图15 不同口径喷嘴的EMD方法分解图Fig.15 EMD method decomposition of differently sized nozzles
6 结 论
(1)通过控制信噪比的方式,选取0.6 MPa气动声源加入炉膛背景噪声,当信噪比为-5dB 时,EMD 方法可以较好地检测到信号特征频率,小波分解出现主峰值7 645 Hz频率干扰,且9 152 Hz频率无法得到有效检测.当信噪比为-14.5dB 时,EMD 方法分解后峰值频率仍为特征频率,但特征频率的最大幅值与炉膛背景噪声EMD 方法分解后的最大幅值无明显差别,小波分解则出现严重干扰.EMD 方法在信噪比大于-14.5dB 时的检测效果明显优于小波分解.
(2)在D-EMD方法的基础上加以改进后提出CD-EMD 方法,将信噪比检测下限降低至-24dB,并且通过各象限取不同初始相位进行对比研究,DEMD 方法出现严重的初始相位干扰,不适用于实际工程应用,而CD-EMD方法能够有效地克服初始相位引起的误判.
(3)CD-EMD 方法可以通过经验阈值的方式判别有无特征频率信号,而且有效地避开了lyapunov等数值计算方法,提高了系统实际运行的实时性及判别准确度.
[1]邵忍平,曹精明,李永龙.基于EMD 小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击,2012,31(8):96-101.
SHAO Renping,CAO Jingming,LI Yonglong.Gear fault pattern identification and diagnosis using timefrequency analysis and wavelet threshold de-noising based on EMD[J].Journal of Vibration and Shock,2012,31(8):96-101.
[2]王文波,张晓东,汪祥莉.脉冲星信号的经验模态分解模态单元比例萎缩消噪算法[J].物理学报,2013,62(6):534-542.
WANG Wenbo,ZHANG Xiaodong,WANG Xiangli.Pulsar signal denoising method based on empirical mode decomposition mode cell proportion shrinking[J].Acta Physica Sinica,2013,62(6):534-542.
[3]HUANG N E,SHEN Z,LONG S R,etal.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings:Mathematical,Physical and Engineering Sciences,1998,454:903-995.
[4]RILLING G,FLANDRIN P,GONÇALVÈS P.On empirical mode decomposition and its algorithms[C]//In Proceedings of the 6th IEEE/EURASIP Workshop on Nonlinear Signal and Image Processing.Italy:NSIP,2003.
[5]杨红英,葛传虎,叶昊,等.基于Duffing振子的天然气管道泄漏检测方法[J].高技术通讯,2010,20(6):628-631.
YANG Hongying,GE Chuanhu,YE Hao,etal.Leak detection based on Duffing oscillators for gas pipelines[J].High Technology Letters,2010,20(6):628-631.
[6]赖志慧,冷永刚,孙建桥,等.基于Duffing振子的变尺度微弱特征信号检测方法研究[J].物理学报,2012,61(5):60-68.
LAI Zhihui,LENG Yonggang,SUN Jianqiao,etal.Weak characteristic signal detection based on scale transformation of Duffing oscillator[J].Acta Physica Sinica,2012,61(5):60-68.
[7]许雪梅,戴鹏,杨兵初,等.光声池中微弱光声信号检测[J].物理学报,2013,62(20):1-9.
XU Xuemei,DAI Peng,YANG Bingchu,etal.Weak photoacoustic signal detection in photoacoustic cell[J].Acta Physica Sinica,2013,62(20):1-9.
[8]胡三高,安宏文,马志勇,等.基于小波奇异值分析的汽轮机碰磨特征提取[J].动力工程学报,2013,33(3):184-188.
HU Sangao,AN Hongwen,MA Zhiyong,etal.Feature extraction of rubbing fault for steam turbines based on wavelet singularity analysis[J].Journal of Chinese Society of Power Engineering,2013,33(3):184-188.
[9]许小刚,王松岭,刘锦廉.基于小波包能量分析及改进支持向量机的风机机械故障诊断[J].动力工程学报,2013,33(8):606-612.
XU Xiaogang,WANG Songling,LIU Jinlian.Mechanical fault diagnosis of fan based on wavelet packet energy analysis and improved support vector machine[J].Journal of Chinese Society of Power Engineering,2013,33(8):606-612.

