风电机组高斯过程回归塔架振动监测研究
郭 鹏,王雪茹
(1.华北电力大学新能源电力系统国家重点实验室,北京102206;2.华北电力大学控制与计算机工程学院,北京102206)
风电机组安装在户外,工作条件恶劣,机组故障率高.通过有效的状态监测和故障诊断方法[1]能够及早发现风电机组部件的早期故障隐患,避免或减小故障带来的损失,对提高风电机组运行的经济性和安全性有重要意义.风电机组的数据采集与监视(Supervisory Control and Data Acquisition,SCADA)系统记录了风电机组各个重要部件的运行数据,这些运行数据中蕴含着机组运行状态的大量信息,对其进行深入分析和处理能够对风电机组部件进行有效的状态监测.Guo等[2]采用非线性状态估计方法建立了风电机组发电机定子温度模型,并对模型预测输出和实际测量发电机温度间的残差进行分析,及时发现了线圈绝缘老化导致的发电机工作异常.Laouti等[3]采用支持向量机建立了风电机组变桨系统模型,能够完成变桨传感器和变桨电机的故障诊断.Feng等[4]根据风电机组齿轮箱的能量传递规律,建立了齿轮箱润滑油温升与风电机组功率的关系模型,当齿轮箱出现异常时,其能量传递效率降低,导致润滑油温升加剧,从而能够发现齿轮箱的早期故障隐患.基于风电机组运行数据的状态监测成本低,实用性强,具有很大发展潜力.笔者基于运行数据开展风电机组塔架振动的监测研究.根据风电机组运行原理,发现影响塔架振动的主要因素,并采用高斯过程回归建模方法建立了塔架与其相关变量间的关系模型,该模型对风电机组运行数据的强随机性和高噪声特点有较好的适应性,并以叶轮变桨系统桨距角不对称故障为例验证了塔架振动监测的有效性.
1 基于运行数据的风电机组塔架振动监测原理
风电机组的SCADA 系统每隔10min记录一次运行数据.以额定功率为1.5 MW 的变速恒频双馈风电机组为研究对象,其切入风速、额定风速和切出风速分别为3 m/s、12 m/s和25 m/s.风电机组运行数据记录的变量不是孤立的,多个变量之间存在密切的关系.以塔架振动为例,其振动幅值会受到运行数据中风速等多个变量的影响,并且在风电机组正常运行时这些相关变量之间的关系是稳定不变的.因此,采用高斯过程回归建模方法对正常运行数据建立塔架振动模型,该模型能够反映风电机组正常运行时塔架振动与相关变量之间的隐含关系,可以用来监测机组运行的异常变化.
塔架振动模型建立完毕后即可开始监测工作.将新的输入量输入塔架振动模型可得到对应的塔架振动预测值.当机组无故障时,塔架振动模型新的输入量和输出量之间的关系与模型记忆的塔架振动特性一致,模型的预测值与实际测量值之间的残差会很小,模型的预测精度很高.当与塔架振动有关的部件出现异常时,塔架振动特性会发生改变,即与风电机组正常运行时相比,此时塔架振动预测值与相关变量之间的关系发生很大改变,此时模型新的输入量与输出量之间的关系偏离模型记忆的塔架振动特性,导致模型预测值偏离实际测量值,二者之间的残差增大,预测精度下降.塔架振动监测过程如图1所示.

图1 塔架振动监测原理图Fig.1 Flow chart of the tower vibration monitoring
2 高斯过程回归建模
2.1 采用高斯过程进行塔架建模的原因
在SCADA 数据中,塔架振动预测值与其他多个变量之间存在的密切关系是由风电机组的运行方式决定的.建立的塔架振动模型能够反映机组正常运行时多个变量之间的关系,可作为基准来监测和发现风电机组在运行中的早期异常变化和故障.
风电机组运行数据具有以下2个特点:
(1)随机性强.风速高时,机组功率、传动链转速和振动加速度等运行变量随风速增大而增大;风速低时反之.运行数据随风速的变化时大时小.当风电机组部件发生异常和故障时,异常信息隐藏在随机变化的复杂的背景运行数据中,发现和提取的难度很大.
(2)含有较大的测量噪声.以运行数据中的风速为例,风速由位于机舱尾部的风速计测得.由于叶轮尾流和偏航误差等因素的影响,风速计测得的风速与机组实际风速间存在偏差,测量噪声较大.此外,由于风电机组处于户外,工作环境恶劣,昼夜温差、风沙和振动等都会导致传感器测得的运行数据存在较大的测量噪声.
用于塔架振动建模的方法必须适合具有上述特点的风电机组运行数据才能达到较好的建模效果.高斯过程回归建模方法是贝叶斯方法的一种,该方法能够灵活地将已有对象的先验知识融合到建模过程中,并采用运行数据进行训练以得到后验高斯过程模型,其本身是一种随机建模方法.
高斯过程的全部统计特性由其均值m(x)和协方差函数k(x,x′)组成,即

由于观测目标值y中含有观测噪声,可建立高斯过程回归的一般模型[5-6]:

式中:ε为独立的白噪声,符合高斯分布,均值为0,方差为,记为ε~N(0,).
设该高斯过程已有N个观测样本数据对(X,y),X={x1,…,xi,…,xN},y={y1,…,yi,…,yN}.由于f(x)和ε均符合高斯分布,则y同样服从高斯分布,其有限观测值联合分布的集合可形成一个高斯过程,即

其中,δij为Kronecker函数,当i=j时,δij=1.
当以矩阵形式表示协方差函数时,有

式中:C(X,X)为N×N协方差矩阵;K(X,X)为N×N核矩阵,其元素Kij=k(xi,xj);I为N×N单位矩阵.
对于符合该高斯分布的新样本,输入为x*,其未知输出为y*,与已有样本(X,y)构成的先验联合高斯分布为
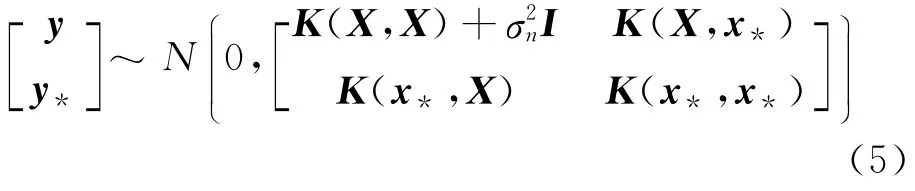
在已有样本数据对(X,y)和输入x*的条件下,y*的后验概率分布为
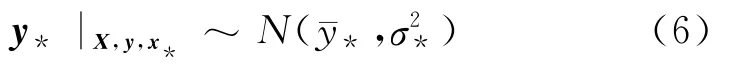

式中:为未知输出y*的预测均值;为未知输出y*的预测方差.
高斯过程回归建模中的协方差函数k(x,x′)是描述建模随机运行数据的重要数字特征,该函数中的参数反映了运行数据之间在不同建模维度上关系的紧密程度.模型中的噪声方差反映了建模数据集的噪声水平.采用高斯过程对运行数据建模即是确定协方差函数参数和噪声方差的过程.协方差函数确定后即可采用式(6)对新的输入量进行输出量的预测.
因此,采用高斯过程回归建模既可以用协方差函数描述风电机组运行数据的随机分布规律,又可以对数据中的噪声进行有效地辨识和分离,适合风电机组运行数据的建模工作.与高斯过程回归建模相比,神经网络和支持向量机在建模时没有考虑对信号中的噪声进行辨识和分离,直接采用含噪声的测量信号建立对象模型,模型在刻画对象特性的同时,不加分辨地把测量噪声也固化在模型中,导致此类模型存在过学习(由于模型固化噪声,导致建模数据集与验证数据集的噪声不同时,模型泛化效果差)和置信风险随模型复杂度增大的问题.将高斯过程应用于连续变量的建模即为高斯过程回归.
2.2 高斯过程回归超参数的确定
采用高斯过程对塔架振动建模的关键是合理确定塔架振动模型的输入量和输出量以及机组正常运行时塔架振动模型的超参数集Θ.笔者采用平方指数协方差函数

其矩阵形式如下:

式中:为向量xi∈RL的第l项;超参数Θ=为包含协方差函数参数与噪声方差的一个向量;表征了高斯过程在输出空间的垂直整体幅度;矩阵D=diag (d1,d2,…,dL)表征了对应每个输入的长度尺度dl的一组集合.
为了获得超参数Θ,采用式(9)的负对数似然函数进行最小化(即最大似然估计,MLE).

上式对超参数Θ的一阶偏导数为
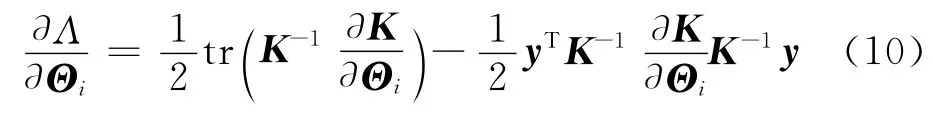
式中:tr(·)为矩阵求迹运算;K(Θ)和Λ(Θ)简写为K和Λ.
采用共轭梯度法即可求得该最大似然问题的解,得到高斯过程回归模型的超参数.
3 塔架振动建模与验证
高斯过程回归建模方法能够很好地适应风电机组运行数据的随机性和高噪声特性.为了建立高斯过程回归塔架振动模型,首先需要确定模型的输入量和输出量.模型的输出量为塔架振动预测值,模型的输入量为运行数据中与塔架振动密切相关的其他变量.塔架振动模型的输入量需根据风电机组的运行原理和运行工况确定.
风电机组的能量来源为风,其运行状态与风速变化密切相关.当风速在切入风速与额定风速之间时,机组运行在最大风能追踪工况.风电机组通过控制发电机励磁转矩来调节叶轮的转速,使叶轮的叶尖速比维持在最佳值附近,以保持叶轮的最佳气动性能,捕获最大风能,在此工况下,叶片的桨距角固定不变.当风速大于额定风速时,为保证风电机组功率不超过额定功率,需要增大叶片的桨距角,从而减小叶轮产生的气动转矩,保证机组功率维持在额定值,在此工况下,运行方式为变桨距恒功率控制.在上述2种不同的工况下,由于运行方式差别很大,与塔架振动相关的变量也不同,因此塔架振动模型需根据工况分别建立.用来进行塔架振动监测研究的运行数据为某台机组2012-03—05期间共约12 000条数据记录.数据采集周期为10 min,每条记录中包括风速、机组功率和塔架振动等近50个变量.
3.1 额定风速以下塔架振动模型及验证
如前所述,在额定风速以下的最大风能追踪控制工况下,叶片桨距角固定.当风速增大时,叶轮和齿轮箱等风电机组的旋转部件转速随之升高,机组功率增大.
塔架振动与其他相关变量的变化趋势如图2所示(运行数据为2012-03-25—29 期间的数据,塔架和传动链振动以加速度表示).从图2可以看出,运行数据中的多个变量与塔架振动加速度的幅值存在相关关系.根据风电机组的运行原理,当风到达叶轮时,会对叶轮产生2个相互垂直的分力:其中一个分力垂直于叶片,产生使叶轮旋转的气动转矩;另一个分力与叶轮扫略平面垂直,平行于机舱的水平轴,该分力会合成为叶轮的轴向推力,激励塔架振动[7].风速越大,该轴向推力也越大,导致塔架振动加剧.塔架振动与转矩和机组功率也有密切关系.由于在额定风速以下,转矩和机组功率随风速的增大而增大,风电机组传动链转速升高,风速的变化反映了风电机组工作的强度,是导致塔架振动变化的重要原因.此外运行数据中的传动链振动与塔架振动也存在密切关系(见图2).传动链振动反映了风电机组主轴、齿轮箱和发电机轴承等振动的大小,而塔架作为传动链和机舱的支撑部件,传动链振动也是影响塔架振动的重要因素.因此,在额定风速以下,高斯过程回归塔架振动模型的输入、输出量见表1.
根据风电机组的运行记录,将2012-03—05的运行数据中机组停机或出现故障时的数据删除后,将风速在切入风速和额定风速之间的每条运行数据中表1所示的5个变量取出构成一个建模样本(不包括图2 中的运行数据),共得到6 206 个.将这6 206个建模样本作为额定风速以下高斯过程模型的建模样本集.采用2.2节方法训练得到额定风速以下塔架振动子模型的超参数(见表2),模型建立完毕.
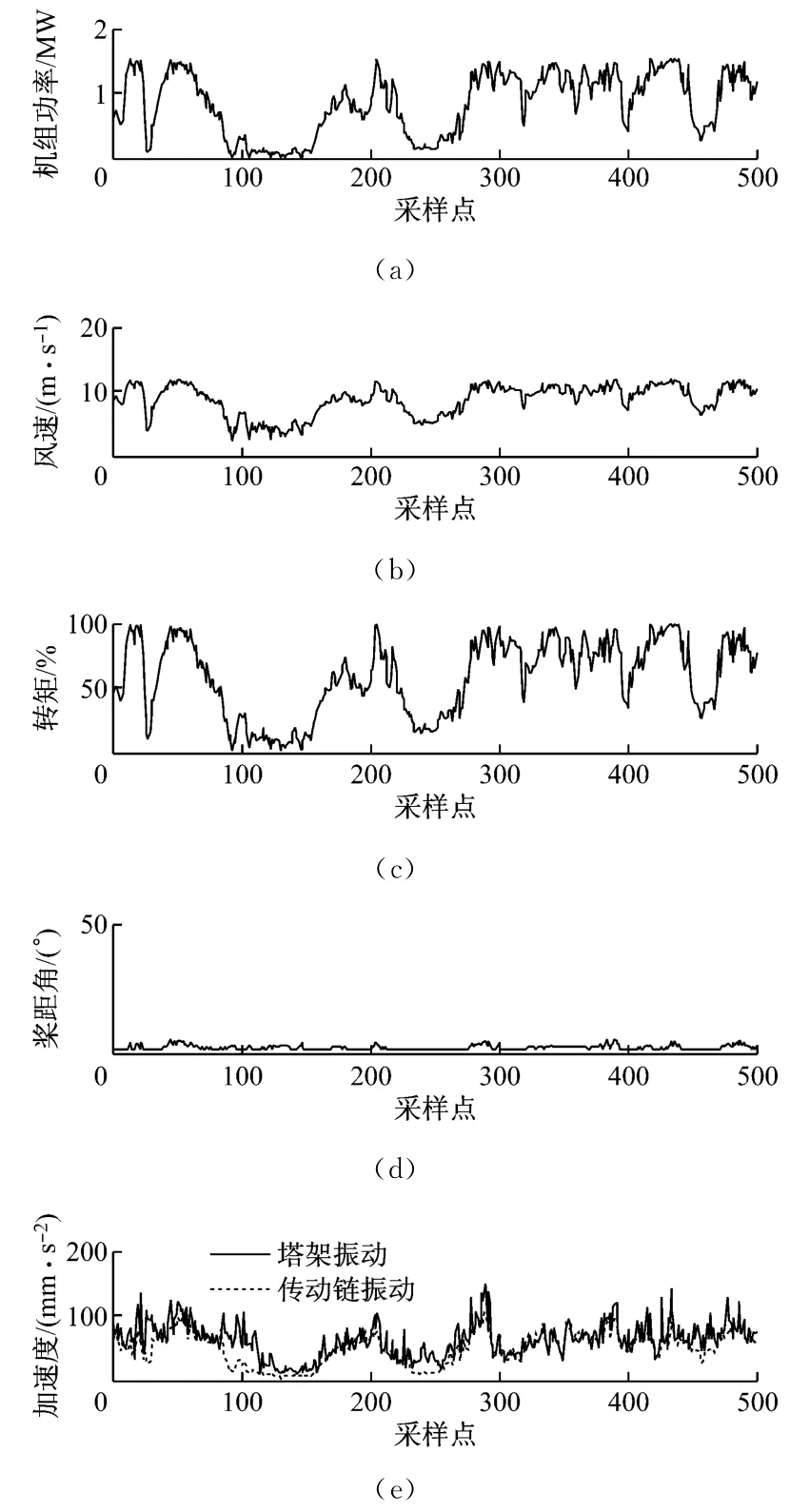
图2 额定风速以下塔架振动及相关变量趋势图Fig.2 Trends of tower vibration and relevant variables at wind speed below rated value

表1 额定风速以下塔架振动模型输入输出Tab.1 Input and output variables of tower vibration model at wind speed below rated value

表2 额定风速以下模型超参数值Tab.2 Hyperparameter data of tower vibration model at wind speed below rated value
采用图2中的500个运行数据对额定风速以下的高斯过程回归塔架振动子模型(模型参数见表2)进行验证,验证结果见图3(除桨距角外,其余变量已归一化).

图3 额定风速以下塔架振动模型验证Fig.3 Validation of tower vibration model at wind speed below rated value
将BP神经网络与高斯过程回归建模效果进行对比.BP神经网络的输入参数为4个,即高斯过程回归模型的输入;输出层节点数为1(即塔架振动);隐含层节点数为20,预测曲线见图3中的虚线.表3为2种建模方法的预测残差均值和均方根误差.由于高斯过程回归建模方法能够适应风电机组运行数据的随机性和高噪声特点,其建模精度较BP 神经网络有很大提高.

表3 额定风速以下2种模型的对比Tab.3 Comparison between two models at wind speed below rated value
3.2 额定风速以上塔架振动模型及验证
在额定风速以上,风电机组工作在变桨距恒功率工况下.此时,机组传动链上的叶轮、齿轮箱和发电机的转速以及机组转矩被控制在额定值附近.对机组功率的调节手段为改变叶片的桨距角.桨距角增大时,叶轮捕获风能减小,机组功率下降;反之亦然.
在额定风速以上,塔架振动与其他相关变量的变化趋势见图4(数据为2012-04-19—29期间部分额定风速以上运行记录).从图4可以看出,机组功率、转矩等基本保持不变.风速和传动链振动仍与塔架振动存在密切关系.同时,桨距角与塔架振动也存在密切关系,这是由于当桨距角发生变化时,叶片的迎风角度随之改变.桨距角增大时,风作用在叶片上产生的升力减小、阻力增大,升力和阻力的这种改变导致气动转矩减小而作用在叶轮上的轴向推力增大,激励塔架振动变化,塔架振动幅值随之发生改变.因此,在额定风速以上,塔架振动模型的输入、输出量如表4所示.

图4 额定风速以上塔架振动及相关变量趋势图Fig.4 Trends of tower vibration and related variables at wind speed above rated value

表4 额定风速以上塔架振动模型输入输出Tab.4 Input and output variables of tower vibration model at wind speed above rated value
将2012-03—05期间正常运行数据中高于额定风速的数据记录整理出来,并将每条记录中表4所示的4个变量取出构成一个样本,得到用于额定风速以上高斯过程回归塔架振动建模的数据样本,共1 135个(不包括图4中的数据).用这些建模数据训练额定风速以上的塔架振动子模型,得到的模型参数如表5所示,模型建立完毕.

表5 额定风速以上模型超参数值Tab.5 Hyperparameter data of tower vibration model at wind speed above rated value
采用图4中的315个运行数据对额定风速以上高斯过程回归塔架振动子模型进行验证,验证结果见图5(除桨距角外,其余变量已归一化).
与高斯过程回归建模对比的BP神经网络输入参数为3 个;输出层节点数为1;隐含层节点数为20,预测曲线见图5中的虚线.2种建模方法的残差均值和均方根误差见表6.由表6可知,额定风速以上塔架振动子模型同样具有很高的建模精度.
4 风电机组塔架振动状态监测实例
第3节中采用历史数据和高斯过程回归建模方法建立额定风速以下和以上的2 个塔架振动子模型.模型建立完毕后,即可开展在线状态监测.将新的运行数据作为模型的输入,模型输出为塔架振动预测值.根据新输入中风速是否高于额定风速,采用对应的子模型进行预测.如图1塔架振动监测原理所示,当模型预测残差较小时,表明塔架振动正常,风电机组相关部件无故障;反之,当模型预测残差异常增大时,预示与塔架振动相关的部件出现异常.
桨距角不对称是一种常见的叶轮故障[8].当该故障发生时,3个叶片的桨距角不一致会导致叶轮气动载荷的不对称,从而使塔架振动激励加剧,对风电机组传动链和塔架有严重的危害.在该风电机组的故障记录中,在2012-04-01T10:51发生桨距角不对称故障,导致机组停机,桨叶向90°偏转进行气动刹车.SCADA 系统中记录的此次停机数据见表7.

图5 额定风速以上塔架振动模型验证Fig.5 Validation of tower vibration model at wind speed above rated value

表6 额定风速以上2种模型的对比Tab.6 Comparison between two models at wind speed above rated value

表7 故障数据Tab.7 Failure data
选取这一停机故障时刻附近的400个记录点作为高斯过程回归塔架振动模型输入,相关变量和塔架振动模型残差的变化趋势如图6所示.
故障停机点在288点处,桨叶向90°偏转进行气动刹车.图6中,在271点之前塔架振动和传动链振动趋势基本一致.在271点之后,塔架振动趋势出现异常,塔架振动和传动链振动幅值出现明显差异.高斯过程回归塔架振动模型捕捉到了模型输入和输出间的这种异常变化,模型预测残差在271点后明显增大,提前近3h检测出了塔架振动的异常变化.在实际运行中,检测出该故障后可以立即停机,避免机组长时间运行在严重影响其寿命的载荷不对称状态.通过对残差设定合理阈值,利用塔架振动模型能够对叶轮故障进行有效监测,阈值设定方法参见文献[9].

图6 叶片桨距角不对称故障趋势Fig.6 Trends of blade angle asymmetry
5 结 论
风电机组运行数据能够反映其关键部件的运行状态,但其强随机性和高噪声的特点给基于运行数据的状态监测带来较大困难.笔者从风电机组的运行数据出发,选取与塔架振动密切相关的变量集,采用高斯过程回归建模方法建立对应不同运行工况的塔架振动子模型,并与BP神经网络方法进行对比,验证了高斯过程回归塔架振动模型的建模精度.利用塔架振动模型能够及时发现对塔架振动有影响的风电机组部件的异常和早期故障.以叶轮变桨系统的桨距角不对称故障为例,验证了塔架振动监测的有效性.
[1]童超,郭鹏.基于特征选择和BP神经网络的风电机组故障分类监测研究[J].动力工程学报,2014,34(4):313-317.
TONG Chao,GUO Peng.Wind turbine fault classification based on BP neural network and feature selection algorithm[J].Journal of Chinese Society of Power Engineering,2014,34(4):313-317.
[2]GUO Peng,INFIELD D,YANG Xiyun.Wind turbine generator condition monitoring using temperature trend analysis[J].IEEE Transactions on Sustainable Energy,2012,3(1):124-133.
[3]LAOUTI N,SHEIBAT-OTHMAN N,OTHMAN S.Support vector machines for fault detection in wind turbines[C]//The 18th IFAC World Congress.Milano,Italy:IFAC,2011.
[4]FENG Yanhui,QIU Yingning,CRABTREE C J.Monitoring wind turbine gearboxes[J].Wind Energy,2013,16:728-740.
[5]RASMUSSEN C E,CHRISTOPHER K I.Gaussian processes for machine learning[M].Cambridge,Massachusetts,USA:The MIT Press,2005.
[6]BRAHIM-BELHOUARI S,BERMAK A.Gaussian process for nonstationary time series prediction[J].Computational Statistics & Data Analysis,2004,47(4):705-712.
[7]贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社,2006:80-89.
[8]KUSIAK A,VERMA A.A data-driven approach for monitoring blade pitch faults in wind turbines[J].IEEE Transactions on Sustainable Energy,2011,2(1):87-96.
[9]WANG Y,INFIELD D.SCADA data based nonlinear state estimation technique for wind turbine gearbox condition monitoring[C]//Proceedings of European Wind Energy Association Conference.Copenhagen,Denmark:European Wind Energy Association,2012:779-785.

