组合磁极无槽PM LSM正弦磁场分析
王明杰, 程志平, 焦留成
(郑州大学电气工程学院,河南郑州450001)
组合磁极无槽PM LSM正弦磁场分析
王明杰, 程志平, 焦留成
(郑州大学电气工程学院,河南郑州450001)
针对传统永磁直线同步电机(PMLSM)齿槽效应及单一磁极产生的非正弦气隙磁场引起电机推力波动,使电机性能变差问题,提出一种组合磁极无槽PMLSM,以提高电机气隙磁场正弦度。建立了组合磁极结构模型,采用分层模型法将气隙磁场叠加,研究消除前三次低频次谐波磁场时,其正弦气隙磁场与电机结构参数及材料特性之间的解析关系式。对比分析了组合磁极和磁极未分段时的气隙磁密、空载反电势及其谐波磁场。研究结果表明当组合磁极中各段磁极长度、剩磁比例系数满足确定约束关系时,气隙磁场中三次、五次、七次谐波均为零,能使气隙磁密和空载反电势趋于标准正弦形,有效消除谐波影响,提高电机性能。解析法和有限元法结果一致证明了理论分析的正确性。
永磁右线同步电机;组合磁极;正弦磁场;剩磁;解析法
0 引 言
永磁直线同步电机(PMLSM)具有推力大、响应速度快、定位精度高等优点在直线运动场合具有较好的应用前景,其不可避免也存在一些缺点,如非正弦气隙磁场引起推力纹波[1]、齿槽效应及端部开断产生的磁阻力引起推力波动[2],均产生振动和噪声。传统PMLSM除开槽引起的齿谐波磁场外,其磁极通常为单一整块磁极(未分段磁极),使磁场中含有大量低频次谐波,影响电机性能。而无槽PMLSM因无齿槽效应对气隙磁场的影响电机磁阻力相对较小,因此磁极产生的气隙磁场正弦度是研究无槽PMLSM一个关键问题。为使电机气隙磁场为正弦,提高电机性能,很多文献对电机磁极结构进行了研究,可归纳为单一磁极和多段磁极两个结构方面的研究。
单一磁极结构方面,常用方法是合理选择磁极极弧系数[3],采用弧形磁极[4],使磁极与气隙交界表面为弧形结构。单一磁极结构通常能消除某一低频次谐波,或者同时消弱相邻两低频次谐波如5、7次,结构参数化优化极弧系数同样耗时耗力,计算效率较低。
多段磁极结构方面,采用磁极分段方法,一个极距下有多段同种材料磁极构成,如两分段磁极[5]、多段等高不等宽磁极间隔排列[6]、多段阶梯式磁极连续排列[7]。采用组合磁极[8-10],由两种不同尺寸和材料磁极紧密排列组成,各段磁极充磁方向可相同也可不同,如“hat”型和“T”型不等高组合磁极[9]。采用halbach磁极结构[11],按正弦规律对磁铁充磁。综上所述多段磁极结构方法多用优化算法改善气隙磁场分布,仅能消除某一低频次谐波,未能在电机本体结构上用解析式表示出正弦气隙磁场与结构参数之间的关联性。
为使气隙磁密为正弦形,同时消除前三次低频次谐波磁场影响,本文采用组合磁极无槽PMLSM结构,建立求解气隙区域矢量磁位方程,研究组合磁极尺寸、材料与磁场正弦特性之间的普遍原理关系式,并用解析法和有限元法对比分析组合磁极和磁极未分段时的合成气隙磁密、空载反电势及其谐波磁场。
1 组合磁极无槽PM LSM结构
采用组合磁极形式,如图1所示,组合磁极由3段采用钕铁硼材料磁极紧密排列组成,中间磁极剩磁大于两端磁极剩磁,中间磁性材料1长度为a,剩磁为Br1,两端磁性材料2长度为b,剩磁为Br2,磁化方向均相同。绕组用非磁性材料固定,环氧树脂灌封,定子为组合磁极和定子轭,动子为绕组和动子轭。
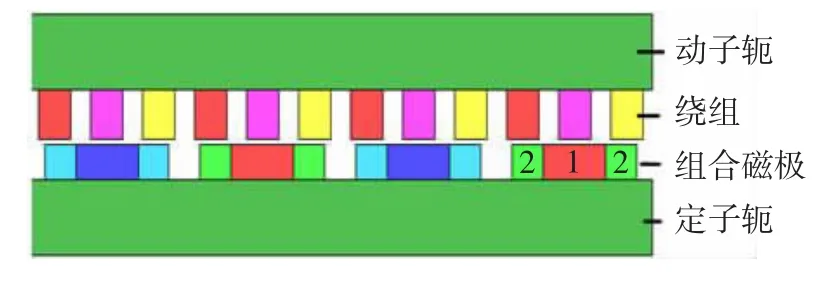
图1 组合磁极无槽PM LSM结构图Fig.1 The structure of slotless PM LSM using modular poles
2 组合磁极气隙磁场解析模型
2.1 单一磁极气隙磁场解析
单一磁极时无槽PMLSM气隙较大,电枢反应很小,只求解永磁体产生的气隙磁场。建立电机分层模型,假设如下:1)各层在x方向无限延伸,永磁体沿y方向均匀磁化,忽略z方向磁场变化;2)永磁体在各方向上磁导率相同且等于空气磁导率;3)铁轭的磁导率为无穷大。以如图2所示模型为求解区域,采用等效磁化强度法求解气隙磁场区域,将永磁体等效成磁化强度分布函数M(x),对其傅里叶分解得
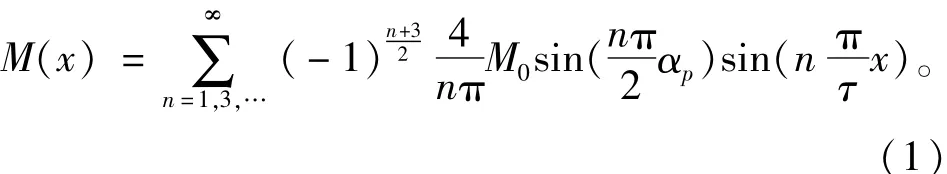
式中:永磁体极弧系数αp=Lm/τ,Lm为未分段时的磁极长;τ为极距;M0=Br/μ0,M0为永磁体磁化强度,Br为永磁体剩磁,μ0为空气磁导率。
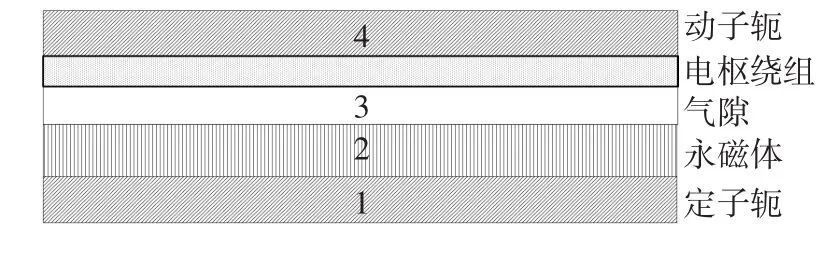
图2 电机模型求解区域Fig.2 Solution region ofmotor model
电机各分区域Maxwell方程气隙区域为22
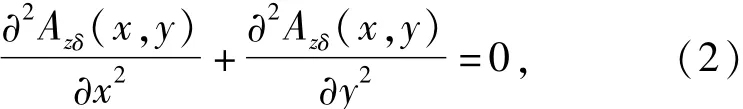
永磁体区域为
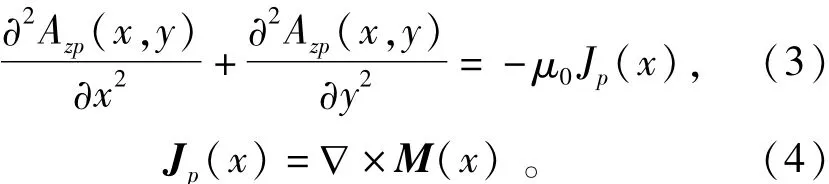
在各区域交界面边界条件满足
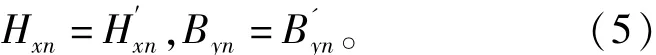
根据式(1)~式(5)推导出气隙磁场区域解析式为
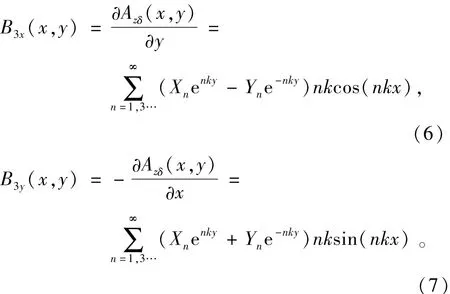
式中:B3x(x,y)、B3y(x,y)分别为沿x方向和y方向的气隙磁密,k=π/τ,τ为极距,Xn、Yn为气隙区域磁密系数,hm为永磁体高;δ为气隙长度,且
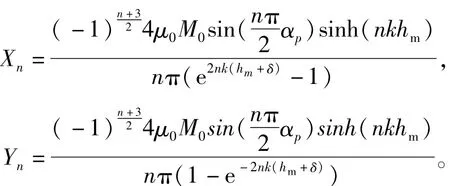
2.2 组合磁极气隙磁场解析
根据图1,利用磁场叠加原理,组合磁极磁场可等效为3段长度为Lm=a+2b的材料2,长度为a的材料2及长度为a的材料1的磁场线性叠加,如图3所示:
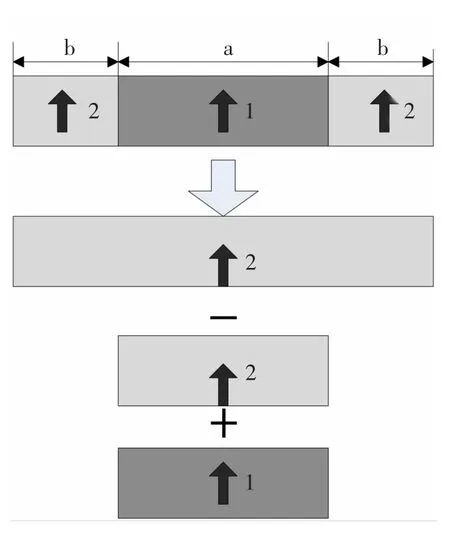
图3 组合磁极磁场叠加Fig.3 Themagnetic field superposition
则各段磁极产生的合成气隙磁密为
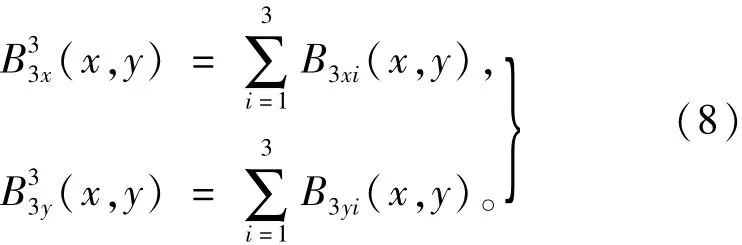
3 组合磁极气隙磁场正弦度分析
根据式(1),单一磁极磁密解析式与参数磁极长Lm、永磁体剩磁Br有 关,知式(6)、式(7)又可表示成
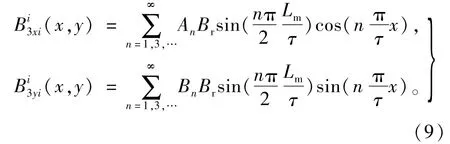
式中,An、Bn为磁密系数,且
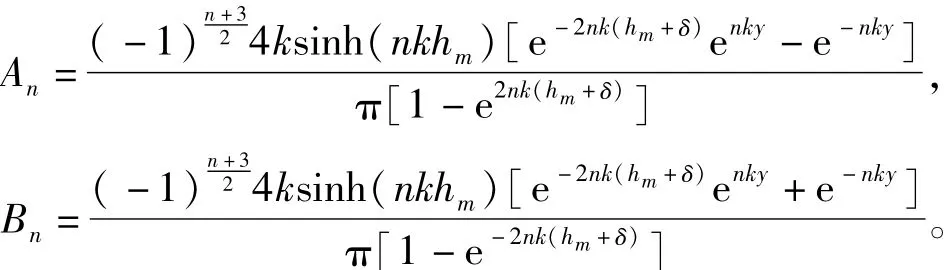
由式(8)、式(9)得组合磁极合成气隙磁密可化简为
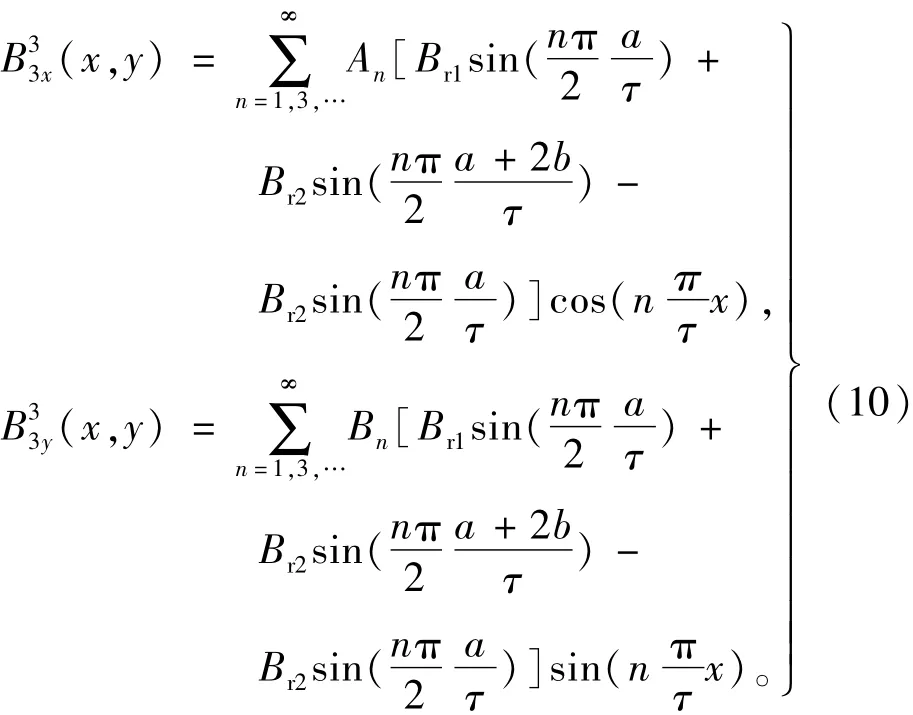

令Br1=kpBr2,kp为组合磁极剩磁比例系数。根据式(10)推出组合磁极磁密比例系数为kzn=可得到以下结论:
1)当kp=1,即采用同一种磁极材料时,相当于单一磁极,只能消除某一频次谐波,消除5次谐波时,由式(11)得a=0.4τ,b=0.2τ,消除7次谐波时
2)当kp>1,即采用组合磁极,当a=0.4τ,b= 0.2τ时,可等效为极弧系数αp=Lm/τ=0.8的单一磁极三分段。无论kp取何值,上式(11)中5次谐波为零,由此得到基波、3次、5次、7次谐波磁密比例系数kzn随kp(取1≤kp≤3)值变化曲线如图4。
3)由图4知,求解方程组式(11)后,kp=1.618时,3次、5次、7次谐波均为0,基波随着kp的增大而增大,基波比未分段时基波增大倍。
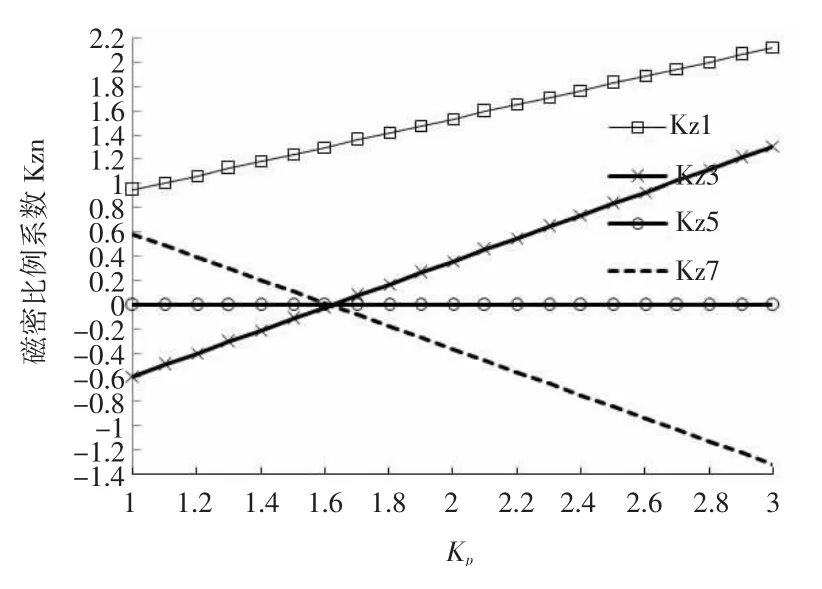
图4 磁密比例系数Kzn随Kp的变化Fig.4 The flux density coefficient Kzn versus Kp
4 实例分析
以一台6极组合磁极无槽PMLSM为分析模型,主要结构尺寸为:绕组宽度wc=8 mm,绕组高度hw=10mm,永磁体高hm=7mm,极距τ=39mm,横向长LFe=120mm,磁极材料1剩磁Br1=1.19 T,解析法得到的组合磁极剩磁比例系数kp=1.618,磁极尺寸a=0.4τ,b=0.2τ。解析法和有限元法得到组合磁极和αp=0.8、剩磁为Br2的单一磁极在平均气隙处合成气隙磁场、基波磁场、所有高次谐波磁场之和对比如图5所示。
图中ANA表示解析法,FEM表示有限元法,B3yz、B3yz1、B3yhz分别对应组合磁极合成气隙磁场、基波磁场、高次谐波磁场之和,By,By1 Byh分别对应单一磁极气隙磁场、基波磁场、高次谐波磁场之和。由图5(a)、(b)、(c)知:
1)两种方法得到的组合磁极和单一磁极磁场结果基本一致,谐波很小使基波磁密与合成气隙磁密曲线基本重合,且组合磁极基波为单一磁极基波的1.382倍,证明了理论分析的正确性。
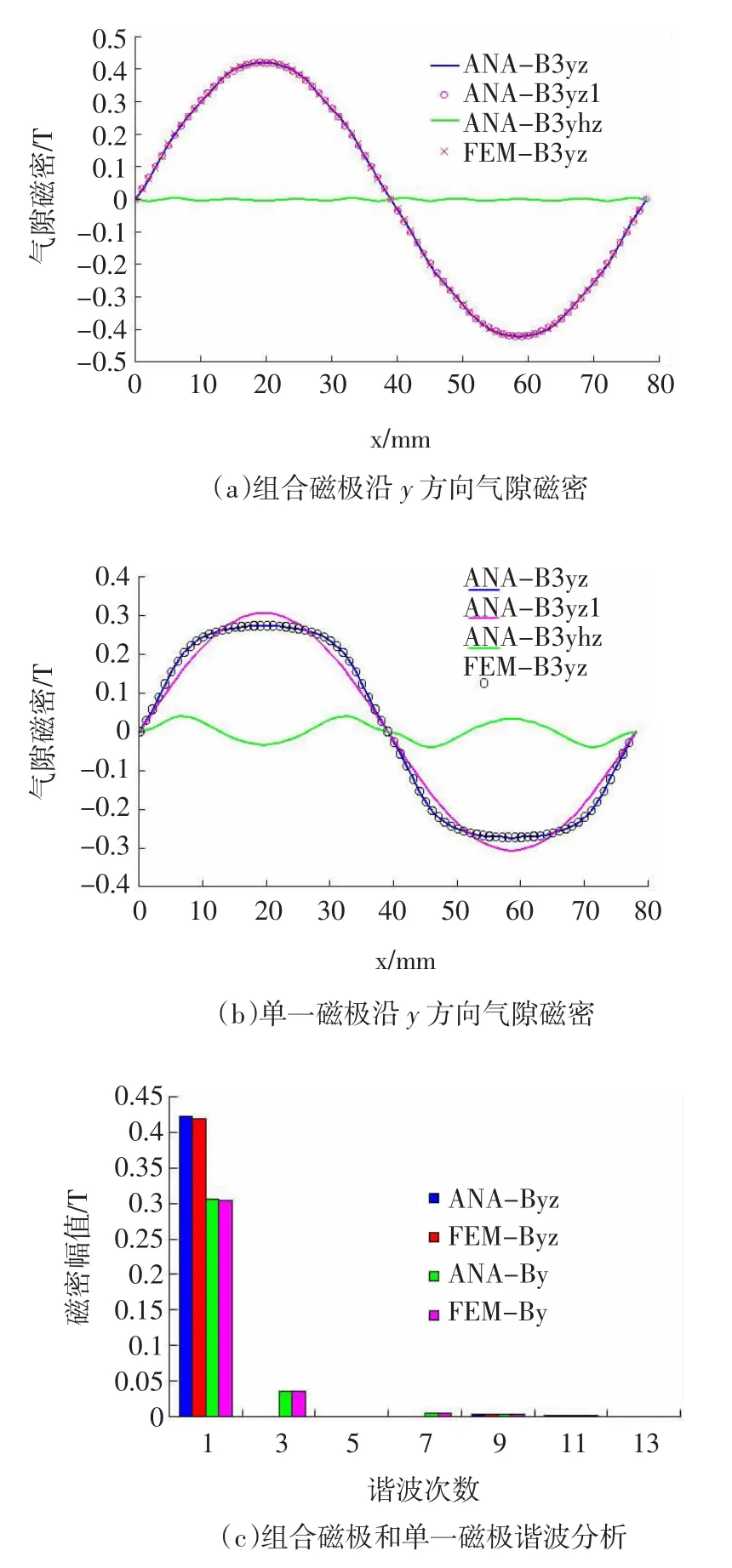
图5 组合磁极与单一磁极沿y方向气隙磁密对比Fig.5 Comparison of flux density By between modular pole and single pole
2)组合磁极中所有高次谐波之和在0.005T内波动,相对其基波幅值很小,谐波影响大幅度降低,而单一磁极在0.04T内波动,相对其基波幅值较大。
3)由图5(c)知组合磁极基波大于单一磁极基波,组合磁极中3次、5次、7次谐波均为0,且9次谐波很小。而αp=0.8的单一磁极5次谐波为0,但存在较大的3次、7次、9次谐波磁场。
为对比组合磁极和单一磁极磁场正弦度的变化,以总谐波失真THD作为评价磁场正弦度的标准,总谐波失真可表示为[10]
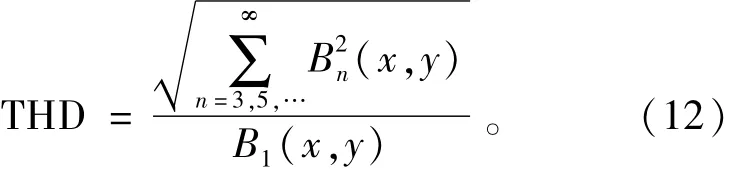
式中:B1(x,y)为基波磁密幅值,Bn(x,y)为n次谐波磁密幅值。
由式(12)计算出αp=0.8的单一磁极THD为11.5%,组合磁极总谐波失真THD为1%,相对单一磁极THD减小了91.3%,很好提高了电机磁密正弦度。以上对分析,对计算如图6(a)、(b)所示,可知与单一磁极相比,组合磁极气隙磁场沿x方向也具有较好正弦度,分析原理同沿y方向磁密。

图6 组合磁极与单一磁极沿x方向气隙磁密对比Fig.6 Com parison of flux density Bx between modu lar pole and single pole
5 组合磁极空载反电势解析
根据已解出的组合磁极气隙磁密,采用e=blv法求解空载反电势。每个线圈感应的电动势为上下两层线圈边反电势之差,取线圈边所在面积区域的平均磁密求解线圈电动势,则
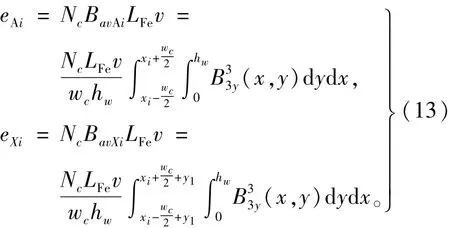
因此得到A相绕组产生的反电势为
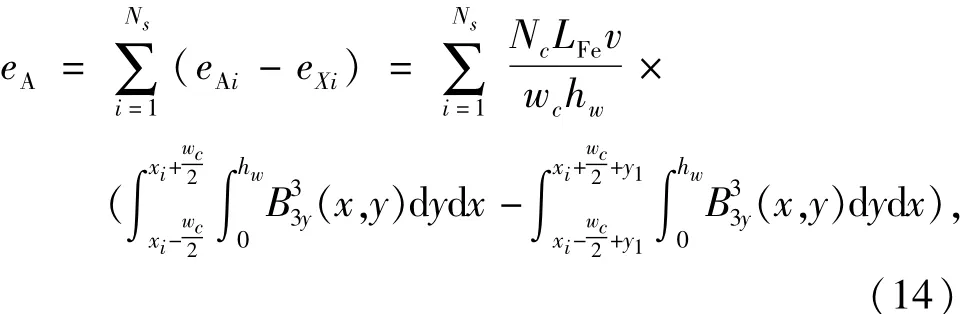
式中,Ns为每相绕组串联线圈数。
当运行频率f=5 Hz时,由解析式(14)得到的空载反电势曲线和有限元结果如图7所示,计算结果表明两种方法得到的反电势结果基本一致,解析法得到反电势基波和合成曲线基本重合,其波形基本为标准正弦形,基波有效值为11.197/1.414=7. 919 V,3次、5次、7次谐波反电势均为0,所有高次谐波之和最大为0.006 V,基本与x=0轴重合,根据式(12)计算出反电势THD为0.11%,因此反电势谐波几乎可以忽略不计,证明了组合磁极结构参数及材料选取的合理性。

图7 解析法和有限元法得到的组合磁极反电动势Fig.7 The EM F ofmodular pole calcu lated by analyticalmethod and FEM
6 结 论
1)建立了单一磁极和组合磁极无槽PMLSM的气隙区域解析模型,计算出合成气隙磁密、基波、谐波磁密,解析法和有限元法结果一致,证明了理论分析的正确性。
2)推导出气隙磁场趋于正弦形时的组合磁极结构尺寸,解析结果表明,a=0.4τ,b=0.2τ时,磁场正弦度和组合磁极剩磁比例系数kp有关。
3)解析法得到kp=1.618时,3次、5次、7次谐波均为0,基波磁密比未分段时增大1.382倍,气隙磁密THD约为1%,气隙磁场具有较高正弦度。
4)计算出组合磁极绕组区域产生的空载反电动势基本为标准正弦形,谐波反电势影响可以忽略不计,证明了组合磁极提高电机性能的有效性。
[1] 李庆雷,王先速,吴丹,等.永磁同步直线电机推力波动分析及改善措施[J].清华大学学报:自然科学版,2000,40(5):34 -36. LIQinglei,WANG Xiankui,WU Dan,et al.Thrust fluctuation analysis and reduction of PMSLM[J].J Tsing hua Univ:Sci& Tech,2000,40(5):34-36.
[2] 王明杰,程志平,焦留成.等间距磁极分段PMLSM磁场及其磁阻力分析[J].电机与控制学报.2014,18(10):74-80. WANG Mingjie,c HENG Zhiping,JIAO Liucheng.Analysis of themagnetic field and detent force in permanentmagnet linear synchronousmotor with equal distance between magnet segmentation[J].Electric Machines and control,2014,18(10):74-80.
[3] ZADEH SV,ISFAHANIA H.Multiobjective design optimization of air-core linear permanent-magnet synchronous motors for improved thrustand low magnet consumption[J].IEEE Transactions on Magnetics,2006,42(3):446-452.
[4] TAVANA N R,SHOULAIE A.Analysis and design ofmagnetic pole shape in linear permanent-magnetmachine[J].IEEE Transactions on Magnetics,2010,46(4):1000-1006.
[5] KIM M Y,KIM Y c,KIM G T.Design of slotless-type PMLSM for high power density using divided PM[J].IEEE Transactions on Magnetics,2004,40(2):746-749.
[6] ISFAHANIA H.Analytical framework for thrust enhancement in permanent-magnet(PM)linear synchronousmotorswith segmented PM poles[J].IEEE Transactions on Magnetics,2010,46(4): 1116-1122.
[7] TAVANA N R,SHOULAIAIE A,DINAVAHIV.Analyticalmodeling and design optimization of linear synchronous motor with stair-step-shaped magnetic poles for electromagnetic launch applications[J].IEEE Transactions on Plasma Science,2012,40(2): 519-526.
[8] 杨玉波,王秀和,朱常青.组合磁极削弱永磁同步电动机转矩脉动方法研究[J].电机与控制学报,2013,17(2):34-37. YANG Yubo,WANG Xiuhe,ZHU changqing.Research ofmodular pole on the reduction of torque ripple of permanent magnet synchronousmotor[J].Electric Machines and control,2013,17 (2):34-37.
[9] SHEN Y,ZHU ZQ.Investigation of permanentmagnet brushless machines having unequal-magnet height pole[J].IEEE Transactions on Magnetics,2012,48(12):4815-4829.
[10] ISFAHANIA H,ZADEH SV,RAHMAN M A.Usingmodular poles for shape optimization of flux density distribution in permanent-magnet machines[J].IEEE Transactions on Magnetics,2008,44(8):2009-2015.
[11] SHEN Y and ZHU ZQ.Analysis of electromagnetic performance of halbach PM brushlessmachines having mixed grade and unequal height of magnets[J].IEEE Transactions on Magnetics,2013,49(4):1641-1649.
(编辑:于智龙)
Analysis on the sinusoidalmagnetic field of slotless PM LSM using modular poles
WANGMing-jie, cHENG Zhi-ping, JIAO Liu-cheng
(School of Electrical Engineering,Zhengzhou University,Zhengzhou 450001,china)
For the problem thatnon-sinusoidal air-gapmagnetic field caused by the sloteffectand the single pole of traditional permanentmagnet linear synchronousmotor(PMLSM)generates thrust ripple and affect the its performance,a structure of slotless PMLSM usingmodular pole was proposed to improve the sine degree of themagnetic field.The structuremodel ofmodular poleswas established,and the superposition of air-gap magnetic field was computed by layermodelmethod.For eliminating the first three low frequency harmonic magnetic fields,the analyticalmethod was used to analyze the relationship between the structure parameters and material characteristicswhen the air-gap magnetic field is sine wave,and to study the flux density,no-load EMF and harmonic magnetic field of the modular pole and single pole. The comparing results show that the 3rd,5th and 7th are both equal to zero,themagnetic field and noload EMF tends to sine wave when the width and remanence ratio of the modular poles satisfy assured constrains.Themotor can effectively eliminate harmonic effects and improve its performance.The validity of theoretical analysis is proved by analyticalmethod and FEM results.
PMLSM;modular pole sinusoidalmagnetic field;remanence;analyticalmethod
10.15938/j.emc.2015.04.006
TM 359.4
A
1007-449X(2015)04-0034-06
2014-9-22
国家自然科学基金(6107507)
王明杰(1982—),男,博士研究生,研究方向为直线电机及其控制;程志平(1974—),男,副教授,研究方向为直线电机及其控制;焦留成(1950—),男,教授,博士生导师,研究方向为直线电机及其控制、电机优化设计。
王明杰

