基于ELM的机器人自适应跟踪控制

李军， 乃永强

(兰州交通大学自动化与电气工程学院，甘肃兰州730070)

基于ELM的机器人自适应跟踪控制

李军， 乃永强

(兰州交通大学自动化与电气工程学院，甘肃兰州730070)

针对刚性臂机器人系统，提出基于极限学习机(ELM)的两种自适应神经控制算法。极限学习机随机选择单隐层前馈神经网络(SLFNs)的隐层节点及其参数，仅调整其网络的输出权值，以极快的学习速度可获得良好的推广性。在自适应控制算法中，ELM逼近系统的未知非线性函数，附加的鲁棒控制项补偿系统的逼近误差。ELM神经控制器的参数自适应调整律及鲁棒控制项由Lyapunov稳定性理论分析得出，所设计的两种控制算法均不依赖于初始条件的约束且放松对参数有界的要求，同时保证闭环系统跟踪误差满足全局稳定而且渐近收敛于零。将所提出的ELM控制器应用于二连杆刚性臂机器人跟踪控制实例中，并与现有的径向基函数(RBF)神经网络自适应控制算法进行比较，仿真结果表明，在同等条件下，ELM控制器具有良好的跟踪控制性能，显示出其有效性和应用潜力。

自适应跟踪控制;极限学习机;单隐层前馈神经网络;刚性臂机器人;算法

0 引 言

由于机器人系统中存在着诸如机器人自身参数误差、观测噪声、未建模动态、负载扰动以及不确定性的外界干扰等因素，因此，针对这种不确定性的在线补偿，不同的控制方法相继被提出。文献［1］引入滤波跟踪误差，设计了自适应神经网络控制器，实现网络的权值在线调整，保证了闭环系统中的所有信号一致最终有界;文献［2］设计的自适应神经网络控制器无须计算机器人的逆动态模型和雅可比矩阵的逆，实现了机器人任务空间的跟踪控制;文献［3］采用自适应模糊系统，针对机器人不确定部分，在同时包括摩擦、外加干扰和负载变化且模糊逼近误差在满足某种假设条件的情况下，设计了基于模型已知，模型未知的两种自适应控制方法，均取得了较好的控制效果;文献［4］采用滑模控制和神经网络相结合，并使用模糊监督控制器，虽然提高了控制系统的性能，但是还须获取系统的先验知识和附加一些限制条件的约束;文献［5］针对非完整移动机器人，通过模糊逻辑与Backstepping方法相结合，在Lyapunov综合法前提下提出了自适应模糊控制方法，平滑的鲁棒补偿器有效地减少了逼近误差及外加干扰;文献［6］针对机器人系统设计了基于自适应模糊控制和自适应鲁棒控制的混合控制器，鲁棒的自适应控制项能有效处理由于外部扰动以及模糊逼近误差和其他建模误差引起的系统不确定性;文献［7］针对水下机器人设计了直接自适应神经网络跟踪控制方法，证明了存在神经网络逼近误差和外部扰动的情况下，水下机器人控制系统的跟踪误差一致稳定有界;文献［8］针对系统参数完全未知且仅输出可测的刚性臂机器人，采用RBF神经网络和高增益观测器设计了一种自适应神经控制算法，实现了沿周期跟踪轨迹对未知闭环系统动态的确定学习，改进了控制系统的性能;文献［9］针对模型不确定的机器人系统设计了基于高斯RBF静态神经控制器的稳定自适应跟踪控制方法，静态神经网络控制器在开关逻辑的监督下完成控制，完整的控制方案可以看作是一个两阶段控制器，基于调制信号的监督Agent能确保轨迹运行在正常范围区域内，这种结构能起到克服多维系统中的“维数灾难”问题;文献［10］针对驱动系统动态的机器人，提出了由PD控制器、前馈补偿器和RBF神经网络补偿器组成的控制方法，该方法不依赖于机器人系统精确动力学模型，仅需要系统的输入输出数据，既保留了PD控制器的优势，又提高了控制系统的跟踪性能;文献［11］针对n自由度机器人系统设计了动态结构模糊神经网络鲁棒自适应控制器，附加的滑模鲁棒项有效地减弱了建模误差，并采用投影算子保证了动态参数的有界性。

极限学习机(ELM)是由Huang［12］等提出的用于SLFNs的快速学习算法。该算法的特点是随机选择SLFNs的隐层节点参数，学习过程中只调节网络的输出权值，因此，与采用梯度下降算法调整所有网络权值参数的SLFNs相比，ELM提高了SLFNs的推广性，具有极快的学习速度。文献［13］针对一类SISO仿射非线性系统，提出了基于ELM的直接自适应神经控制算法。

鉴于ELM的优点，本文针对刚性臂机器人系统，提出基于机器人不确定项整体逼近与分块逼近的两种自适应ELM神经控制算法，利用ELM逼近系统的未知非线性函数，附加的鲁棒控制项补偿系统的逼近误差。所获得的两种控制器均不依赖于初始条件的约束且放松对参数有界的要求，并应用Lyapunov稳定性理论证明系统在存在未知外界干扰、摩擦力、负载变化以及建模逼近误差条件下，基于ELM网络的系统控制律及相应的参数自适应调节律均能保证闭环系统的稳定性。最后，将含有不同隐层节点激活函数的ELM控制器应用于二自由度平面刚性臂机器人系统中，在同等条件下，与RBF自适应控制算法进行比较，以验证本文控制算法的有效性。

1 ELM学习算法

1.1 具有随机隐层节点的SLFNs

对于含有L个隐层节点，m个输出节点的SLFNs的输出可以描述为

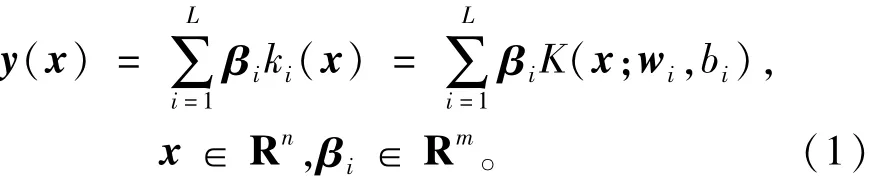
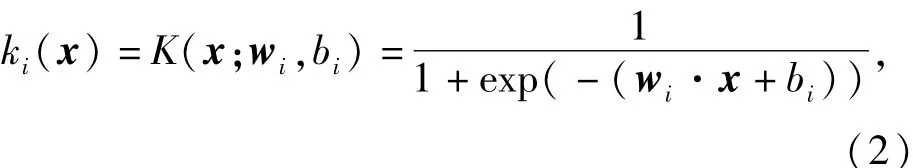
其中wi∈Rn，bi∈R，符号.表示内积。

若为RBF类型节点(RBF nodes)，其激活函数为

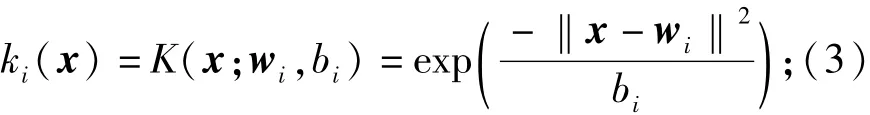
其中wi∈Rn，bi∈R+。

1.2 ELM算法

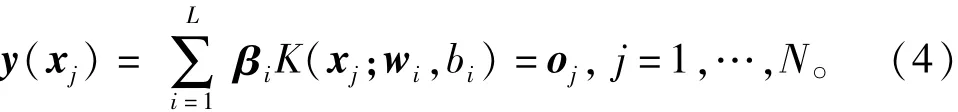
以矩阵形式表示为

式中

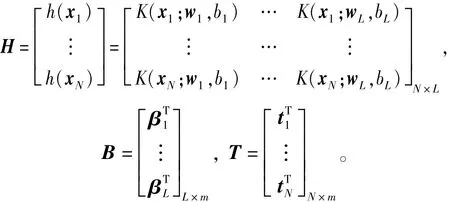
其中:H为SLFNs的隐层输出矩阵，H的第i列表示与输入x1，x2，…，xN相关的第i个隐层节点的输出向量。矩阵H的第i行表示与输入xi相关的隐层特征映射，即隐层特征映射定义为

如果激活函数k在任意区间上无限可微，且SLFNs隐层节点及节点参数可以随机生成。存在如下定理

定理1［14-15］给定任意小的正数ε(ε＞0)和任意区间上无限可微的激活函数k:R→R，N组任意给定的不同训练样本在以概率1收敛的任意连续概率分布下，存在L≤N，对于在Rn×R的任意区间上随机生成的SLFNs隐层节点参数成立。

从插值的思想看隐层节点的最大数目L应当小于训练样本的数目N。事实上，L=N时，训练误差将为零。由定理1，当L小于N时，SLFNs将以很小的训练误差逼近训练样本，且矩阵H并非方阵，从而存在使得

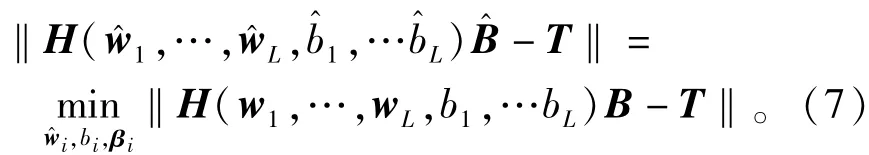
式(8)中，权值最小范数的最小二乘解为

其中H†为矩阵H的Moore-penrose广义逆。

2 ELM的自适应跟踪控制

2.1 机械臂动力学模型及其结构特性

考虑一个n关节的刚性臂机器人模型，其动力学方程为

机器人系统的动力学特性如下

特性1 惯性矩阵M(q)是正定对称矩阵且有界，I为单位矩阵，存在正数m1，m2满足不等式m1I≤M(q)≤m2I。

2.2 基于ELM整体逼近的控制器设计

跟踪误差定义为

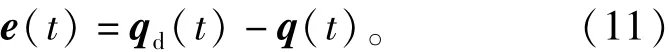
其中qd(t)为期望轨迹。

滤波跟踪误差定义为

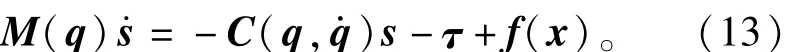
实际应用中，模型不确定项f(x)未知，因此需要采用单输出的ELM网络分别对不确定项f(x)中的每个元素进行逼近，则式(6)中的矩阵B∈此时成为L×1的列向量，而针对输入x，式(6)中的矩阵H此时成为1×L的行向量h(x)。则用于逼近的ELM网络具体可表达为

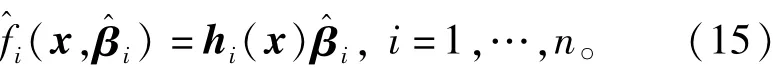
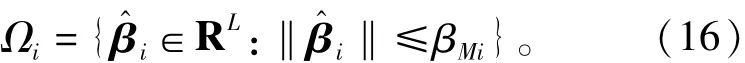
其中βMi为设计参数，L表示ELM网络隐层节点的个数。

其中D表示x的有界紧集，则权值估计误差为

ELM逼近误差为

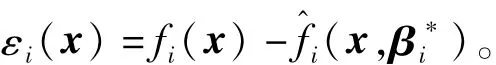
假定紧集D足够大，保证对所有x∈D，最小逼近误差有界，即|εi(x)|≤¯εi，∀x∈D，其中¯εi为未知常量，i=1，…，n。

由上述分析，则可得到

其中Kv=diag{kv1，kv2，…，kvn}(kvi＞0)为控制增益矩阵。

为了进一步减少对模型的逼近误差，还可引入鲁棒控制项τr。而且在实际的工程中，模型最小逼近误差的上界往往无法确定，即逼近误差的上界也需要通过适当的自适应律在线进行调整。

定理2 考虑式(10)的机器人系统，若满足期望轨迹qd∈Rn光滑有界，且存在光滑有界的假设条件，若设计具有鲁棒性的控制律为

商家回应：您反馈的食材问题小店非常重视，小店选用食材都是当天采购，绝对新鲜的。这个问题希望您可以和小店取得联系，将事情核实。一定给您满意的结果。

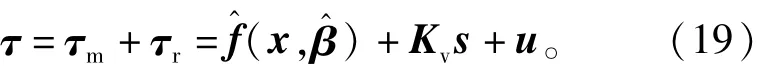
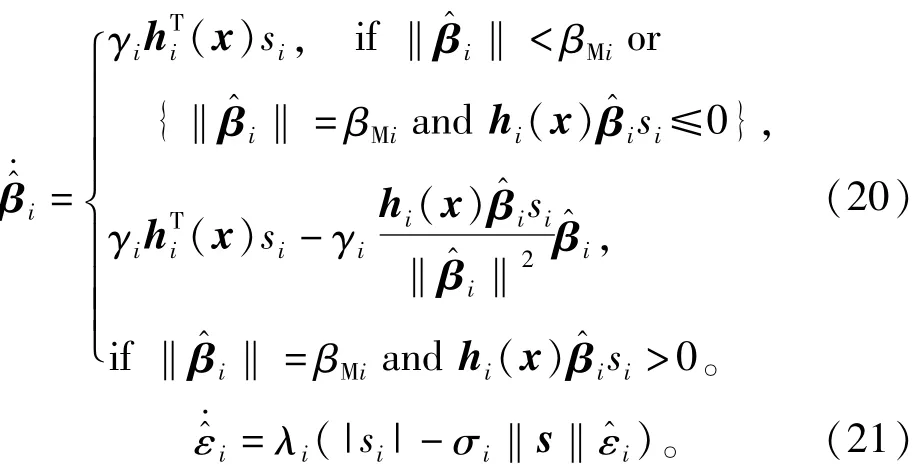
证明 首先基于如下假设

假设1 对于任意给定正常数ωi，有

将控制律式(19)代入式(13)可得

选择Lyapunov函数为

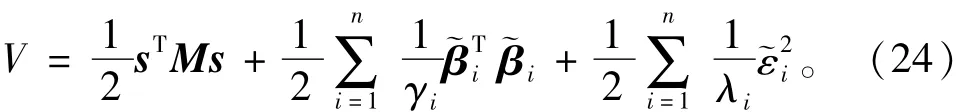
对式(24)微分，并将式(23)代入得

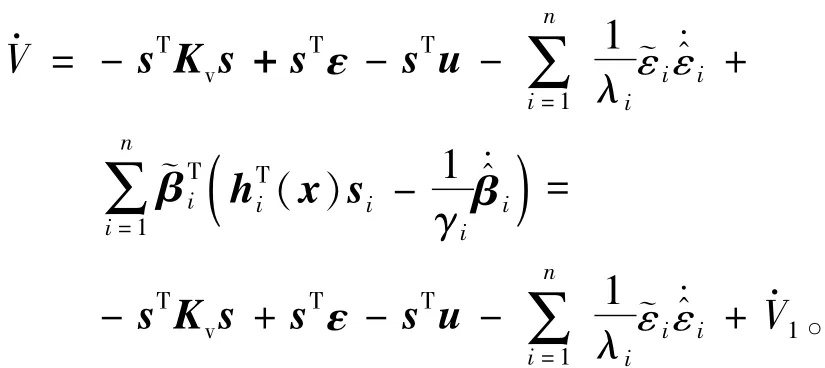
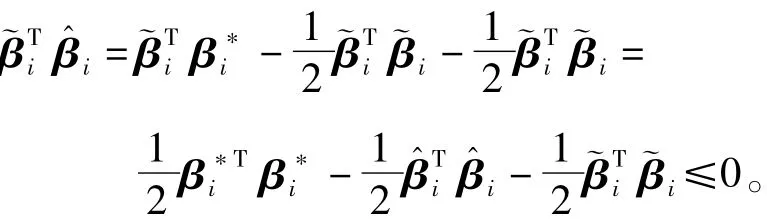
因此，无论权值自适应律取何种形式，均能保证

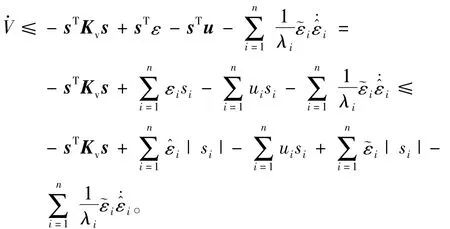
将式(21)代入上式得

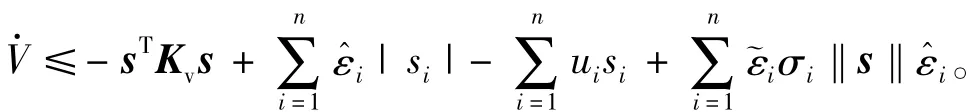
由假设1可得

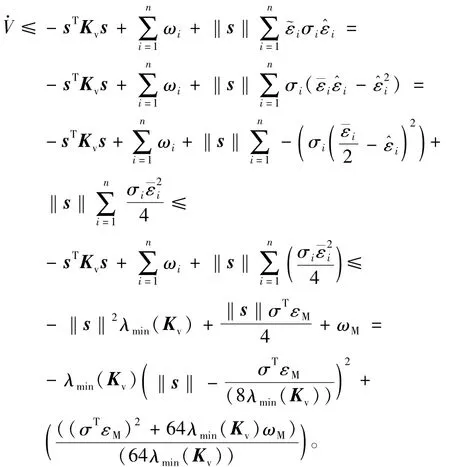
则有

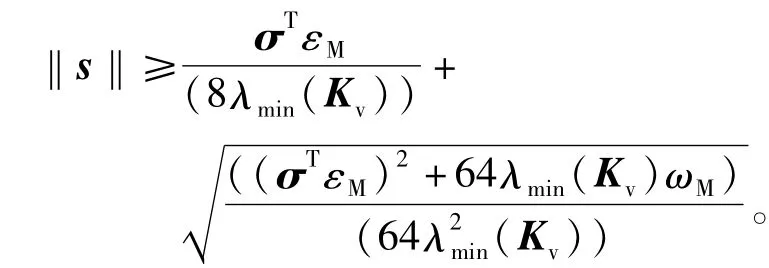
2.3 基于ELM网络分块逼近的控制器设计

由式(14)可知，被控对象中的f(x)可写为

f(x)=M(q)q¨r+C(q，q.)q.r+G(q)+F(q，q.，q¨)。

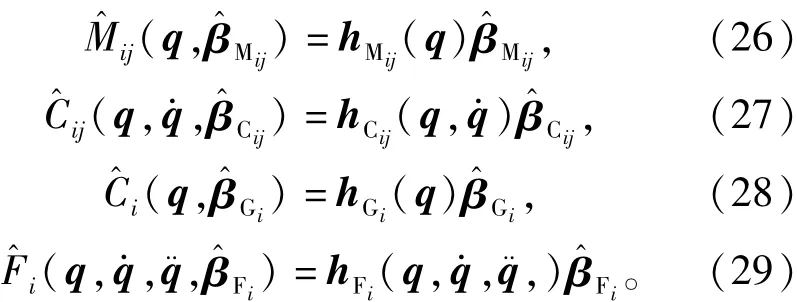
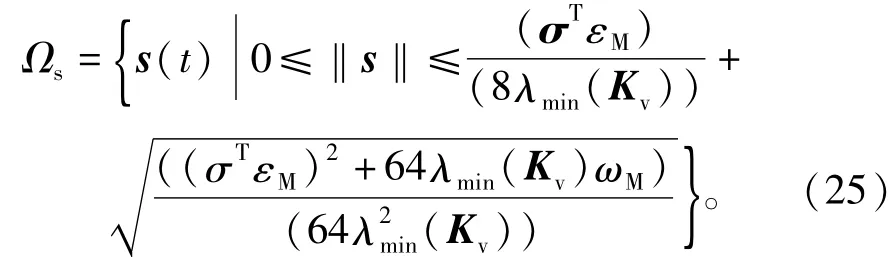
由式(25)可知，在紧集Ωs之外ELM网络的输出权值向量表示ELM网络的隐层输出，i，j=1，…，n。

由式(16)及式(17)可知，ELM网络的权值估计误差为

ELM网络的逼近误差如下

根据以上分析，则有

定理3 考虑式(10)的机器人系统，若满足期望轨迹qd∈Rn光滑有界，且存在光滑有界的假设条件，若设计具有鲁棒性的控制律为

其中

其中σMij＞0、σcij＞0、σGi＞0、σFi＞0为设计常数，i，j= 1，…，n。则控制律式(30)可保证闭环系统所有信号一致最终有界，且轨迹跟踪误差及其导数渐近收敛于零，即当t→∞时，e(t)，e.(t)→0。

证明 首先将式(13)改写为

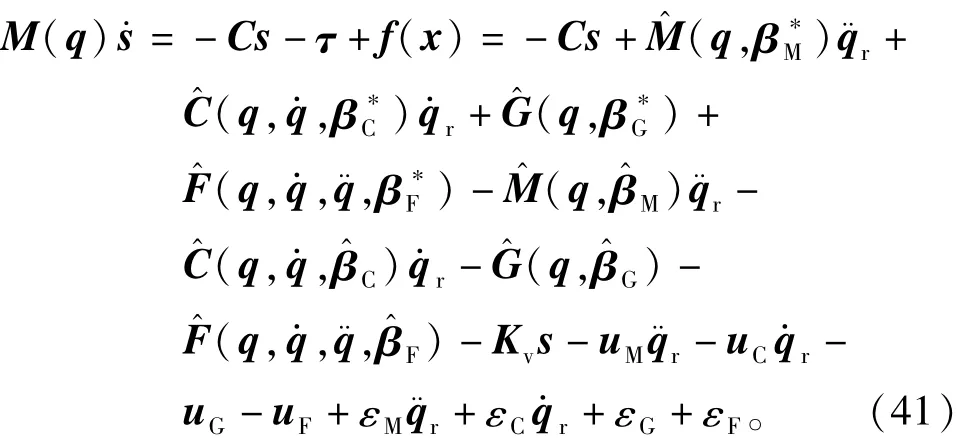
选择Lyapunov函数为

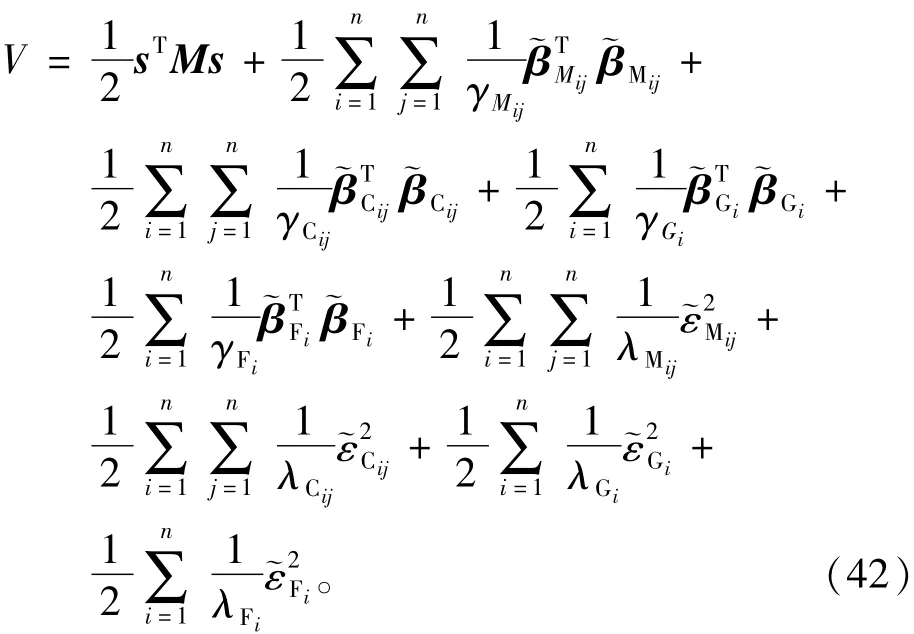
对式(42)微分，并将式(41)代入得

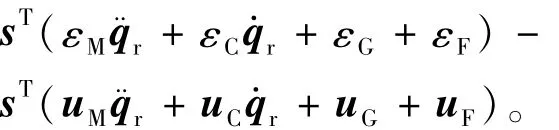
根据机器人特性2，并将式(33)～式(36)代入上式，与定理2的证明相似，则有

由假设1可得

则有

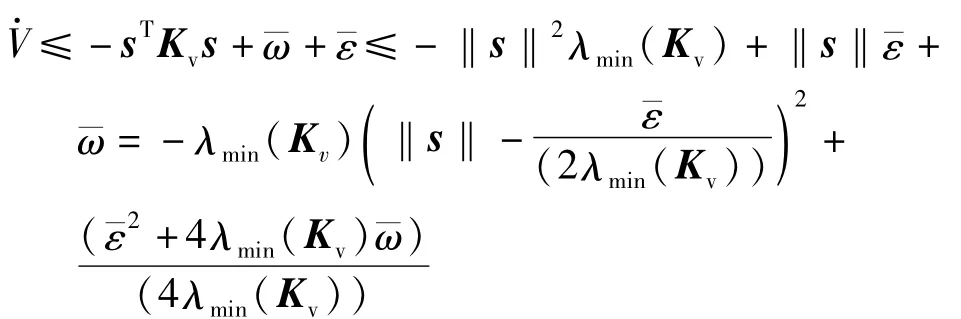
其中λmin(Kv)表示矩阵Kv的最小特征值。紧集定义为

与定理2的分析类似，同样得出控制律式(30)可保证闭环系统的所有信号一致最终有界，且跟踪误差及其导数渐近收敛于零。因此，定理得证。

3 仿真研究

为了验证所设计的ELM自适应控制算法的有效性，选择二自由度平面刚性机械臂为被控对象进行仿真，并与RBF网络自适应控制方法在同等条件下进行比较。机械臂的动力学模型为方程(10)，其各参数为［16］

其中，q1和q2分别为关节1和关节2的角度和分别为关节1和关节2的角速度;m1和m2分别为连杆1和连杆2的质量;l1和l2分别为连杆1和连杆2的长度;g为重力加速度。摩擦力和外界干扰分别表示为

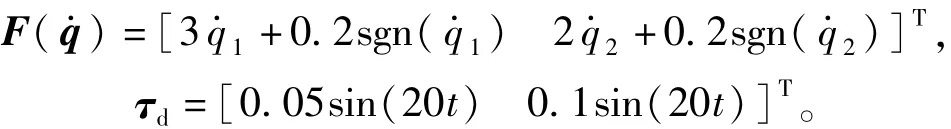
机械臂动力学方程中的参数为

l1=l2=1.0 m，m1=0.8 kg，m2=2.3 kg，g= 9.8m/s2。系统的初始状态选择为

实验中，ELM网络的隐层节点分别考虑RBF型节点及可加性节点，RBF型节点的隐层激活函数选择高斯函数，即K(x;w，b)=exp(-‖x-w‖2/b);可加性节点的隐层激活函数选择Sigmoid函数，即K(x;w，b)=1/(1+exp(-(w.x+b)))，隐层节点参数(w，b)分别在［-1，1］和［0，1］之间分别随机选择。

RBF神经网络自适应控制方法中的径向基函数选择高斯基函数所有RBF网络隐层节点的中心矢量值分别按输入值的有效映射范围来取，即针对输入为q时，取值范围为［-1.5，1.5］，针对输入为q.时，取值范围为［-1，1］，基宽取值为0.1。

3.1 仿真一

应用ELM对系统不确定项进行整体逼近，此时控制律取式(19)，参数自适应调节律取式(20)、式(21)。设计参数选择为:控制增益矩阵Kv= diag{50，50}，Λ=diag{20，20}，λi=25，σi=0.4，ωi=5，i=1，2，ELM与RBF网络的隐层节点个数均为L=25。控制的目标是使系统的输出q1和q2分别跟踪期望轨迹qd1=sin(t)和qd2=cos(t)。

从图1及图2中可以看出，与RBF控制器相比，当机器人系统存在模型不确定性、未知摩擦力和外界干扰，同时存在未知逼近误差限的情况下，采用ELM网络设计的自适神经应控制算法取得了更好的轨迹跟踪效果。

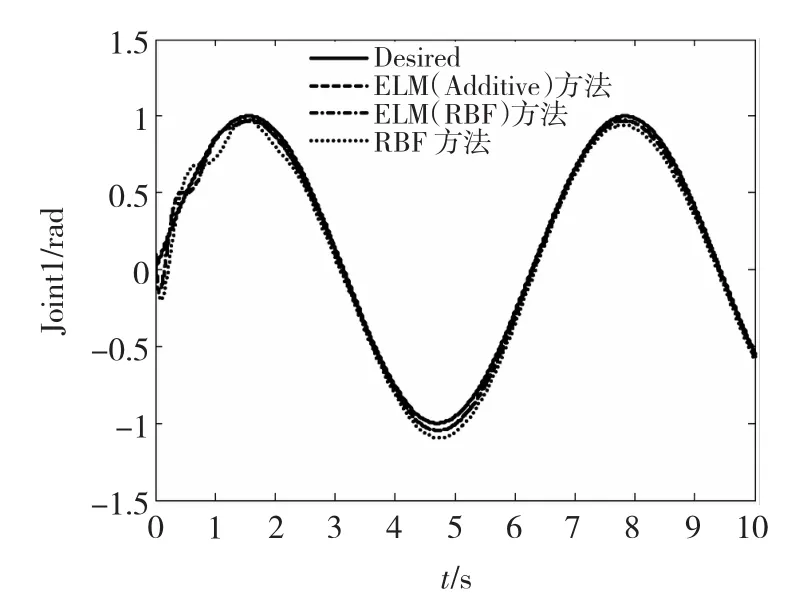
图1 关节1位置跟踪Fig.1 Position tracking of joint 1

图2 关节2位置跟踪Fig.2 Position tracking of joint 2

从图3及图4可以看出，在整个控制过程中，ELM控制器的控制输入信号处于平滑有界状态而没有高频抖振现象发生。从图5及图6中可看出，应用ELM网络进行整体逼近所设计的自适应控制器具有更好的跟踪性能，位置跟踪误差渐近收敛于零的一个很小的邻域内，与RBF控制算法相比，收敛速度更快。

图3 关节1控制输入Fig.3 Control input of joint 1

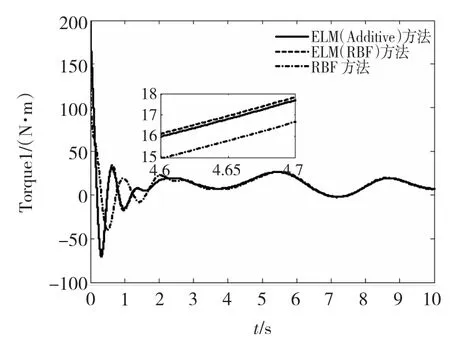
图4 关节2控制输入Fig.4 Control input of joint 2

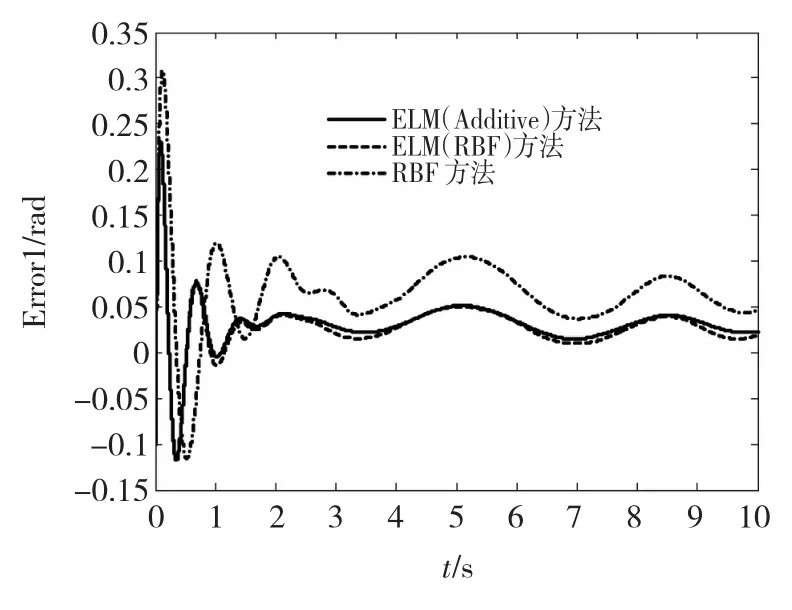
图5 关节1跟踪误差Fig.5 Tracking error of joint 1

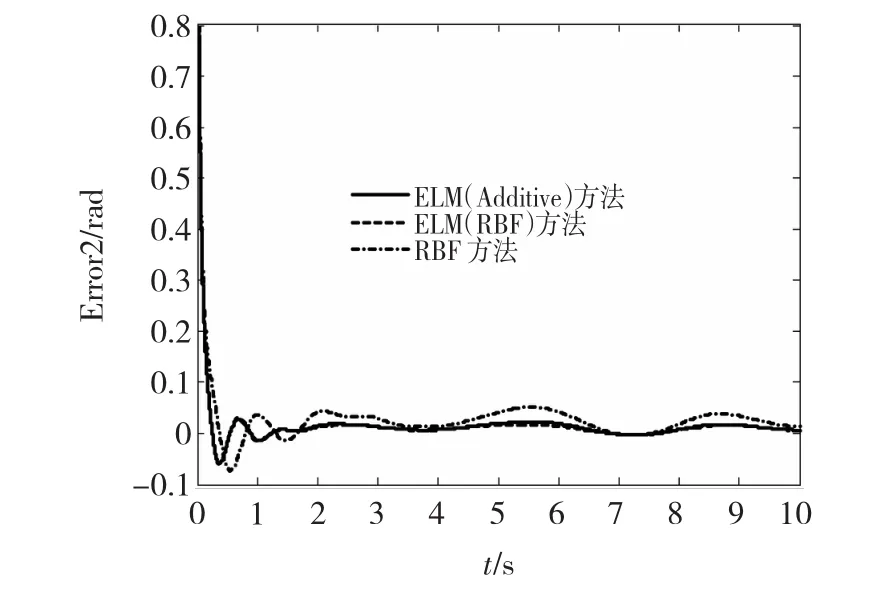
图6 关节2跟踪误差Fig.6 Tracking error of joint 2

3.2 仿真二

采用对不确定项分块逼近的情况下，控制律取式(30)，参数自适应调节律取式(33)～式(40)。

设计参数选择为:控制增益矩阵Kv=diag{50，σGi=0.02，σFi=0.02，i，j=1，2。每个ELM网络的隐层节点个数均选取L=20。为进一步验证ELM控制器的有效性，还与RBF控制器进行了仿真对比，每个RBF网络的隐层节点个数均选取L=20。控制的目标是使系统的输出q1和q2分别跟踪期望轨迹和

从图7及图8中可以看出，当机器人系统存在模型不确定性、未知摩擦力和外界干扰时，且在逼近误差限未知的情形下，与应用ELM网络对不确定项进行整体逼近相比，采用不同激活函数的ELM网络对机器人系统不确定项进行分块逼近时，具有更好的跟踪性能，达到了预期的跟踪效果。而且在同等条件下，与RBF网络自适应控制算法相比，ELM控制算法显示出更好的跟踪效果。

图7 关节1位置跟踪Fig.7 Position tracking of joint 1

图8 关节2位置跟踪Fig.8 Position tracking of joint 2

从图9及图10可以看出，在整个控制过程中，ELM控制器的控制输入信号平滑有界。从图11及图12中可看出，与整体逼近的控制算法相比较，基于ELM的分块逼近自适应控制算法进一步提高了系统的控制精确度。上述仿真结果证实了所提出ELM控制器能很好地对不确定性机器人系统进行跟踪控制，具有良好的跟踪性能。

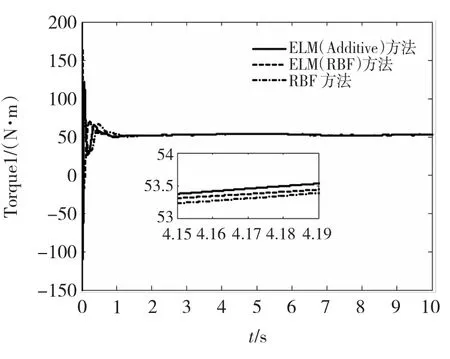
图9 关节1控制输入Fig.9 Control input of joint 1

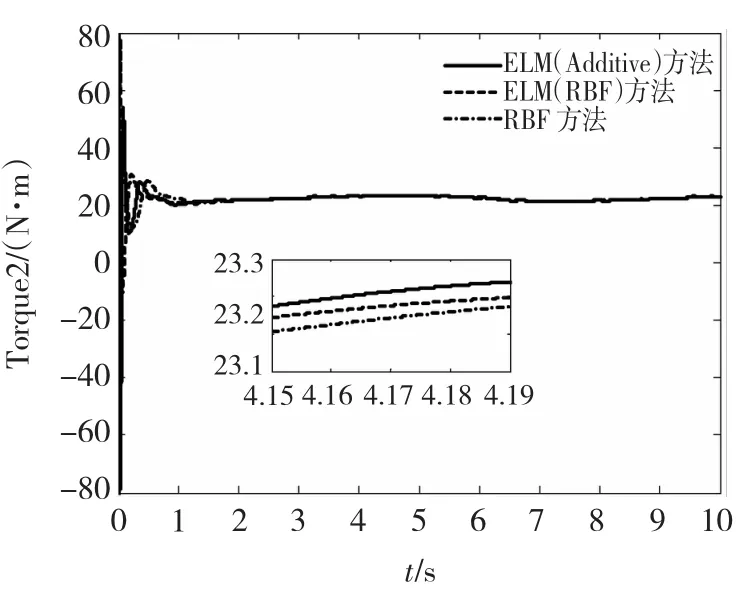
图10 关节2控制输入Fig.10 Control input of joint 2

图11 关节1跟踪误差Fig.11 Tracking error of joint 1

图12 关节2跟踪误差Fig.12 Tracking error of joint 2

5 结 论

针对具有模型不确定性、未知摩擦力、外界扰动以及负载变化的刚性臂机器人系统，提出针对系统不确定项进行整体逼近与分块逼近的两种ELM自适应神经控制算法，利用ELM逼近系统的未知非线性函数，附加的鲁棒控制项补偿系统的逼近误差。所获得的两种控制器均不依赖于初始条件的约束且放松对参数有界的要求。系统的自适应控制律，ELM网络的权值及未知逼近误差限的自适应参数调节律均是在基于Lyapunov稳定性理论分析设计的基础上得到，且两种ELM控制算法均能保证闭环系统的稳定性及跟踪误差的最终一致有界。此外，分段设计的ELM网络权值自适应调节律还具有投影算子的特性，保证了权值有界。通过应用于二自由度平面机器人的仿真实例验证了ELM控制器的良好跟踪性能，仿真结果表明了ELM自适应控制算法的有效性和鲁棒性。

［1］ LEWIS F L，LIU K，YESILDIREK A.Neural net robot controller with guaranteed tracking performance［J］.IEEE Transactions on Neural Networks，1995，6(3):703-715.

［2］ GE SS，HANG c c，WOON L c.Adaptive neural network control of robotmanipulators in task space［J］.IEEE Transactions on Industrial Electronics，1997，44(6):746-752.

［3］ YOO B K，HAMW c.Adaptive controlof robotmanipulator using fuzzy compensator［J］.IEEE Transactions on Fuzzy Systems，2000，8(2):186-199.

［4］ HU H，WOO PY.Fuzzy supervisory sliding-mode and neural-network control for robotic manipulators［J］.IEEE Transactions on Industrial Electronics，2006，53(3):929-940.

［5］ HOU ZG，ZOU A M，c HENG L，etal.Adaptive control of an electrically driven nonholonomic mobile robot via backstepping and fuzzy approach［J］.IEEE Transactions on control Systems Technology，2009，17(4):803-815.

［6］ ISLAM S，LIU PX.Robustadaptive fuzzy output feedback control system for robot manipulators［J］.IEEE/ASME Transactions on Mechatronics，2011，16(2):288-296.

［7］ 俞建成，李强，张艾群，等.水下机器人的神经网络自适应控制［J］.控制理论及应用，2008，25(1):9-13. YU Jiancheng，LIQiang，ZHANG Aiqun，etal.Neural network adaptive control for underwater vehicles［J］.control Theory and Applications，2008，25(1):9-13.

［8］ 吴玉香，杨梅，王聪.从机器人输出反馈自适应神经网络控制中学习［J］.控制与决策，2012，27(11):1740-1745. WU Yuxiang，YANG Mei，WANG cong.Learning from output feedback adaptive neural control of robot［J］.control and Decision，2012，27(11):1740-1745.

［9］ Mulero-Martinez J I.Robust GRBF static neurocontroller with switch logic for control of robotmanipulators［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23(7): 1053-1064.

［10］ 王良勇，杨枭.带有前馈和神经网络补偿的机械手系统轨迹跟踪控制［J］.电机与控制学报，2013，17(8):1-6. WANG Liangyong，YANG Xiao.Trajectory tracking control for robotic manipulators endowed with feedforward and neural networks［J］.Electric Machines and control，2013，17(8):1-6.［11］ c HEN c S.Dynamic structure neural-fuzzy networks for robust adaptive control of robotmanipulators［J］.IEEE Transactions on Industrial Electronics，2008，55(9):3402-3414.

［12］ HUANG G B，ZHU Q Y，SIEW c K.Extreme learning machine:a new learning scheme of feedforward neural networks［c］//Proceedings of International Joint conference on Neural Networks，July，25-29，2004，Budapest，Hungary.2004:985 -990.

［13］ RONGH J，ZHAOG S.Directadaptive neural control of nonlinear systems with extreme learning machine［J］.Neural computing and Applicatiuijions，2013，22(3-4):577-586.

［14］ HUANG G B，ZHU Q Y，SIEW c K.Extreme learning machine:theory and applications［J］.Neurocomputing，2006，70 (1):489-501.

［15］ HUANG G B，WANG D H，LAN Y.Extreme learning machines:a survey［J］.International Journal of Machine Learning and cybernetics，2011，2(2):107-122.

［16］ Lewis F L，Abdallah c T，Dawson DM.control of robotmanipulators［M］.New York:Macmillan，1993.

(编辑:刘素菊)

Adaptive tracking control of a rigid armrobot based on extreme learning machine

LIJun， NAIYong-qiang
(School of Automation and Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，china)

Based on extreme learning machine(ELM)，two adaptive neural control algorithms for rigid arm robot system were presented.ELM for signle-hidden layer feedforward neural networks(SLFNs)，which randomly chooses hidden node parameters and analytically determines the outputweights of SLFNs，tends to provide good generalized performance at extremely fast learning speed.Within these adaptive control algorithms，ELM was employed to approximation the plant's unknown nonlinear function and robust control term was used to compensate for approximation error.Parameter adaptive laws and robust control term of ELM controllerswere derived based on Lyapunov stability analysis so that global stability and asymptotic convergence to zero of tracking errors can be guaranteed.Futhermore，two adaptive controllers do not depend on any parameter initialization conditions and relax the requirementof bounding parameter values.The proposed adaptive ELM control algorithmswere then applied to a tracking control instance for two-link rigid arm robot and compared with existing radial basis function(RBF)neural control algorithms.Simulation results show that ELM controllers have good tracking performance and demonstrate the effectiveness of the proposed control algorithms.

adaptive tracking control;extreme learning machine;signle-hidden layer feedforward neural networks(SLFNs);rigid arm robot;algorithm

10.15938/j.emc.2015.04.017

TP 273

A

1007-449X(2015)04-0106-11

2014-05-19

国家自然科学基金(51467008);甘肃省高等学校基本科研业务费专项资金项目(620026)

李 军(1969—)，男，博士，教授，研究方向为计算智能与系统建模、预测与控制;乃永强(1987—)，男，硕士研究生，研究方向为机器人建模与控制。

李 军