基于看板的汽车生产物流超市物料配送优化研究
丁佳祺,张 镓,蔡三发
(同济大学 经济与管理学院,上海 200092)
基于看板的汽车生产物流超市物料配送优化研究
丁佳祺,张 镓,蔡三发
(同济大学 经济与管理学院,上海 200092)
以成本最优为目标,考虑了车间资源有限等约束条件,探索了基于看板的循环配送方式在物流超市物料配送系统中的应用,为最优循环时间和看板数量提供了决策方案。
看板;物流超市;混流装配线;成本优化
1 引言
为了满足日益增长的产品多样性需求,汽车生产采用柔性化的混流装配线,即一条装配线可以生产多种不同类型的汽车,这就要求在生产过程中对装配线上不同的车型提供相应的零部件,一旦没有及时供应,则可能造成生产线停工。为此,汽车制造企业引入物流超市的概念,通过看板拉动系统实现零部件有节拍、有秩序地上线配送,有利于汽车生产的持续进行,降低汽车生产成本[1]。
目前,国外对物流超市物料配送的研究主要集中在装配企业的运作决策方面,如运输车数量、运输路线、包装箱大小等。Mauricio等(2008)以最小化存储成本和处理成本为目标,探讨在包装容器容量有限条件下,零部件配送上线时所需包装容器的数量[2]。Veronique等(2012)以成本最小化为目标,对批量供应和成套供应进行权衡[3]。Faccio等(2013)通过实证研究表明运输能力、供应策略与运输车数量之间存在高度相关性,运输能力受到零件尺寸的约束[4]。国内对物流超市的研究则起步较晚,以理论研究为主,在混流生产物料配送方面,通常围绕库存成本、运输成本、运输时间和服务相应水平展开,规划物料配送的频率、配送量和运输线路等[5]。
建立汽车物流超市的最终目的是为了服务于生产,将零部件高效率、低成本地运送至生产线旁。因此,本文将通过分析汽车生产物流超市到装配线的物料配送流程,考虑牵引车运输能力和车间空间等约束,建立成本优化模型,得到汽车零部件的最佳配送循环周期和最优的看板数量(即最少的线边库存)。
2 配送流程分析
物流超市,顾名思义是具备超市一般特点的物流产品与服务的自选商场。汽车生产物流超市是生产所需物资的缓存区,具备零部件卸货、缓存、分拣、换装、排序等功能[6]。传统的物流配送由供应商仓库直接将物料配送至生产线,运输距离长,而汽车生产所涉及的零部件数量和种类繁多,为了避免物料供应不及时,通常配送的批量较大,有些零部件还需要进行包装转换、排序等处理,导致原本空间有限的生产车间秩序混乱。物流超市的应用实质上是在仓库和生产线之间设置了中间存储区,将物料换装、排序等作业与生产线分离,它的数量可以是一个或者多个,只在需求产生的时候向生产线配送相应需求量的物料,具有小批量、多频率的配送特点。
本文的研究范围为汽车生产物流超市到装配线的零部件供应,以看板为需求信息传递的媒介来控制整个物料配送系统的物料流和信息流,通过牵引车将物料及时、准确地被配送到相应的装配工位,保证装配线的持续、高效运行。看板拉动系统的运作流程分为4个步骤:
(1)补货操作员到各工位收取消耗完的空箱及看板箱内的看板;
(2)补货操作员将空箱运送到空箱放置处,再根据看板到物流超市拣选相应数量和种类的零部件;
(3)补货操作员在下一个配送时间点,将必要数量和种类的零部件配送至相应装配工位的线边货架,同时收取空箱和看板;
(4)空箱返回,根据看板进行零部件拣选,即开始下一个配送循环。
看板卡上包括物料的零件号、名称、数量、在物流超市中的存放位置、装配线需求工位等信息,零部件的配送以标准周转箱为单位,一张看板卡包含了一个标准箱的零件数量,即每一个装配工位所需每种零部件的线边库存水平与该零部件对应的看板数量有关。若看板数量增加,则装配线旁相应的零部件库存量也相应增大,造成库存成本增加,并且会大量占用装配线旁的空间;若看板数量减少,装配线旁的零部件库存量也相应减少,此时为了避免该装配工位发生缺货,必须使零部件配送次数更加频繁,增加了物料配送成本。因此,汽车生产物料配送系统的总成本最优就是使库存成本和配送成本之和最小,从而确定最优的看板数量和循环周期。
3 优化模型构建
3.1 模型假设
为了简化模型,提出以下假设:
(1)每一条装配线能够生产同一系列的多种产品,而不同装配线之间生产的产品系列不同。因此,每一种产品与装配线之间存在一一对应关系。每一种零部件能够被用于不同的装配线,但只能用于该装配线的某一个固定工位。
(2)生产平准化是准时制生产的前提条件,因此,每条装配线的日生产量被认为是一个常数。
(3)装配线上各产品的历史需求服从于正态分布,零部件需求是关于产品需求和物料清单的函数,因此,每个装配工位的零部件需求也服从于正态分布。
(4)每种零部件均采用标准周转箱包装,每一个标准箱与一个看板卡相联系,周转箱的容量则取决于零部件的尺寸。
(5)本文的研究对象是从物流超市到装配线的物料配送过程,因此,所考虑的库存成本是与看板数量有关的生产线旁的运转库存,不包括物流超市中的库存,因此,考虑到汽车生产物料配送的连续性,必须保证物流超市不存在缺货情况。
3.2 符号说明
m—能够生产的产品类型,m=1,…,M;
i—生产所需的零件类型,i=1,…,I;

Dil—装配线l上零部件i的平均日需求量
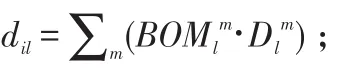
σil—装配线l上零部件i的需求标准差,可通过Das和Tyagi(1999)公式得到:
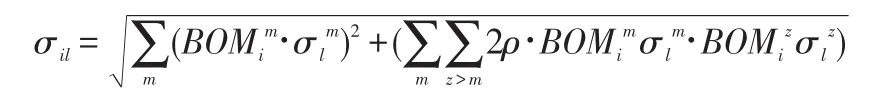
其中,ρ为相关系数,ρ=-1/(M-1),M为产品种类数[7]。
Lrun—牵引车完成一次物料配送的行驶距离,单位:m;
Tw—每日工作时间,单位:min;
t—牵引车完成两次配送之间的间隔,即循环周期;
N—牵引车平均每日的配送循环次数,N=Tw/t;
Kanbani,l—装配线l上零部件i的看板数量。
3.3 模型建立
本模型的建立是基于汽车生产物流超市对装配线实施看板循环配送的环境下,配送系统由一个物流超市和多条混流装配线构成。
(1)目标函数。配送系统优化以某一时期内的运营成本最优为目标,包括该时期内产生的库存成本和配送成本,见式(1)。叉车、牵引车、货架、包装箱等设施设备的成本属于固定资产投入,不包含在其中。

其中,CTOT为考虑周期内系统产生的总运营成本;CIn为考虑周期内时间内的库存成本;CTp为考虑周期内时间内的配送成本。
①库存成本。库存成本与装配线旁的平均库存量、单位库存成本相关。通常情况下,库存成本占零部件价值的25%到55%,主要受价格、税费、保险、仓库租赁费用、占地面积和库存控制的影响。而在汽车生产中,由于装配线旁的空间有限,增大零部件库存会阻碍装配作业,因此,库存持有成本系数通常被认为超过55%[7],见式(2)。

其中,ci为零部件i的价值;hi为零部件i的库存持有成本系数;Iˉil为装配线l上零部件i的平均线边库存量,可以通过零部件i的需求量和平均配送次数计算得到,见式(3)。

2 配送成本。物料配送成本与配送次数、单次配送成本相关。虽然每次配送的时间是确定不变的,但每次的配送量不一定相同,单次配送量受到牵引车运输能力和配送零件物理特性的限制,如零件的尺寸、重量等,而这些特性也会影响到拣选器具的选择。为了简化模型,单次配送成本只考虑牵引车的燃油费和人工等固定费用,见式(4)。

其中,p1为牵引车行驶单位距离产生的燃油费;p2为单次配送过程中产生的固定费用,包括车辆维修费、配送人员工资等。
将式(2)、(3)、(4)代入式(1),得式(5):

为了求得总运营成本CTOT的最小值,对式(5)进行求导,得到总运营成本最优化情况下的循环周期t。

(2)约束条件。补货操作员从收到看板到完成物料拣选、排序、分装等流程存在一定的时间间隔,而牵引车从物流超市行驶到装配线也需要一个缓冲时间,因此,物料配送的循环周期必须满足物料准备时间。

其中,t1为补货操作员收到看板信息并做出拣货安排的反应时间;t2为零部件拣选、排序、分装的作业时间,与零部件存放位置、搬运设备效率等因素有关,考虑到操作员的熟练程度,在正常运作的情况下,每次作业时间的变动很小,可以认为是一个恒定值;t3为牵引车在配送过程中往返于物流超市和装配线的运输时间,是关于物流超市到装配线之间的距离以及牵引车运输速度的线性函数;t4为零部件装车和卸载的时间。
牵引车在运输时可以悬挂多个拖车,但是受到动力性能的限制,其运输能力有一个上限,如最大运输重量。在本文研究的系统中,零部件配送以标准周转箱SKU为单位,因此,将最大运输SKU数量作为牵引车运输能力Q的指标。牵引车平均每次配送的运输量必须满足它的运输负荷。
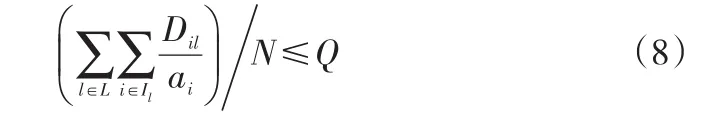
其中,ai为一个SKU能够装载零部件i的数量;Dil/ai为装配线l上零部件i平均每日所需的SKU数量。
此外,由于生产车间的空间有限,零部件的线边库存数量必须符合存放条件,见式(9)。

其中,DilTw∙t+k∙σilt为装配线l上零部件i的最大库存量,k∙σilt为安全库存,k是安全因素;Ssku为单个标准周转箱的占地面积;线边库存采用流利式货架,Nh为货架层数;Wa为线边库存区宽度,La为线边库存区长度。
通过上述约束条件,最终可以得到成本最优化时的循环时间t,从而根据丰田公式,得到最优的看板数量,[]表示取整。

4 算例
以某汽车生产厂内物料配送系统为例,该系统包括1个物流超市和2条混流装配线,每条装配线可生产三种不同款式的车辆,平均日生产量分别为12、5、10和15、8、20,所有产品的变异系数均为20%。每款汽车的物料清单、零部件容量及价值见表1。
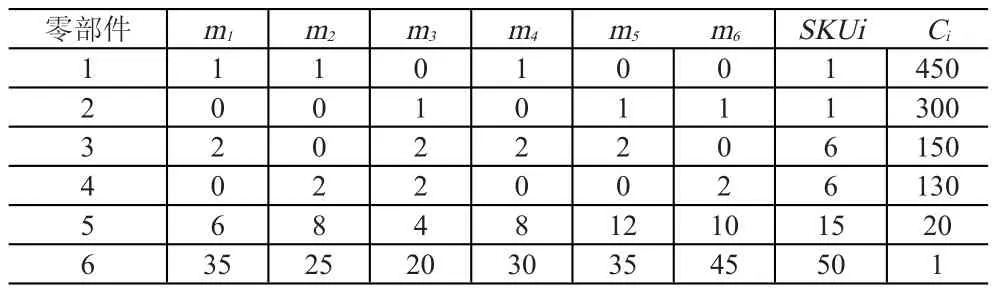
表1 物料清单及零部件属性
生产车间每天工作8h,一年工作250d。牵引车运输线路总长800m,平均运输时间2m/s。操作员收到看板信息的反应时间为1min,拣选、排序等作业时间5min,装卸零部件时间为1min。牵引车行驶单位距离的燃油费为4元/km,单次配送产生的人工等固定费用为80元,零部件库存持有成本占到零件价值的55%。牵引车运输能力为30个SKU,每条装配线旁最多可存放60个SKU。库存服务水平99.97%(k=3.5)。
系统原本循环时间为45min,年运营成本622 346.2元。根据本文的成本优化模型进行求解,得到循环时间t等于33.49min(0.56h)时,年运营成本最低为596 167.5元,节约了26 178.7元,如图1所示。
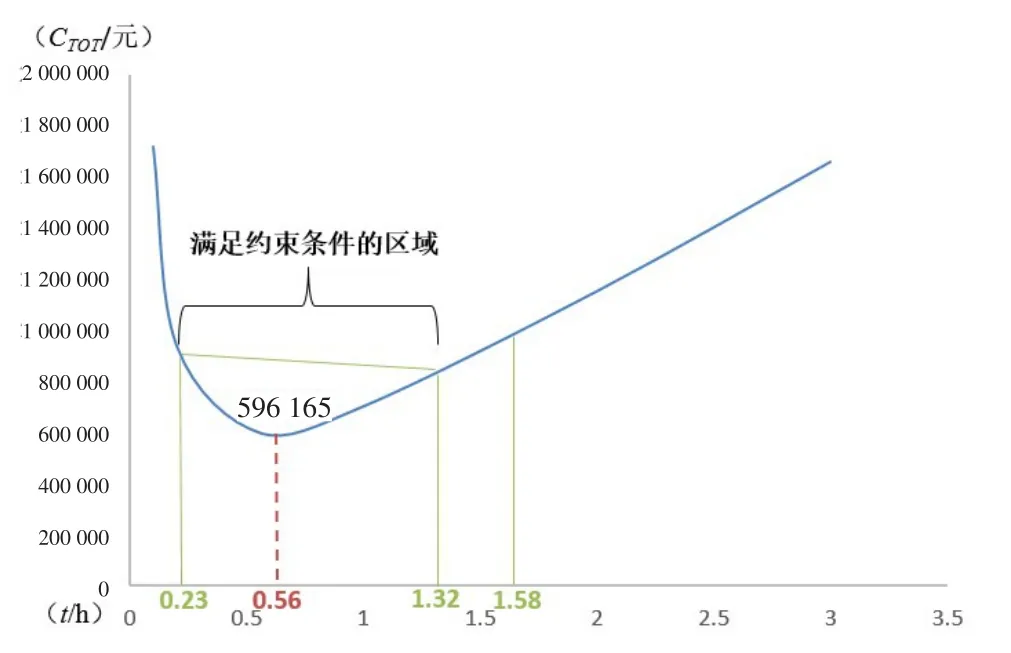
图1 循环时间t与年运营成本CTOT关系图
表2给出了四种不同条件下的循环时间的边界值,以及对应的成本情况。

表2 方案比较
从图3和表2可以看出,最优配送循环时间必须满足一定的取值范围。当最小备货时间大于成本最小的时间,取最小备货时间为最优循环时间;当t值的上限小于成本最小的时间,取该上限值为最优循环时间,而t值的上限取决于牵引车运输能力和线边库存能力的比较。在本配送系统中,成本最小时的时间取值满足t的取值范围,因此,循环时间0.56h、看板数量30即为最优选择方案。
5 总结
物流超市在汽车生产物流的应用中有其它物流方式不可替代的优点,它对于产品种类多、批量小、产品切换快等特点有着非常强的适应能力[7]。基于看板的物料配送方式更适用于需求量变化较小、且消耗连续的通用性较强的零部件,在汽车生产中还涉及一些体积大、通用性低或者体积小、配置数量多的零部件,可以采用顺序供应、单量份配送等方式。未来将根据零部件的分类,探索多种配送方式在汽车生产中的应用,进一步完善物流超市物料配送流程。
[1]C Sendil Kumar,R Panneerselvam.Literature review of JIT-KANBAN system[J].International Journal of Advanced Manufacturing Technology, 2007,(32):393-408.
[2]Mauricio C de Souza,Carlos R V de Carvalho,Wellington B Brizon. Packing items to feed assembly lines[J].European Journal of Operational Research,2008,(184):480-489.
[3]Veronique Limere.To kit or not to kit:optimizing part feeding in the automotive assembly industry[J].International Journal of Production Research,2012,50(15):4 046-4 060.
[4]Maurizio Faccio,Mauro Gamberi Alessandro Persona.Design and simulation of assembly line feeding systems in the antomotive sector using supermarket,kanbans and tow train:a general framework[J].Journal of Management Control,2013,(24):187-208.
[5]李晋航.混流制造车间物料配送调度优化研究[D].武汉:华中科技大学,2012.
[6]郑秀恋,刘陆.物流超市在汽车生产物流中的应用研究[J].物流技术, 2013,32(7):80-85.
[7]Maurizio Faccio,Mauro Gamberi Alessandro Persona.Kanban number optimization in a surpermarket warehouse feeding a mixed-model assembly system[J].Inernational Journal of Production Research,2013,51 (10):2 997-3 017.
[8]俞杰.物流超市在工厂内部的应用[J].工业工程与管理,2004,(9):131-133.
Study on Distribution Optimization of Automobile Production Logistics Supermarket Based on Kanban System
Ding Jiaqi,Zhang Jia,Cai Sanfa
(School of Economics&Management,Tongji University,Shanghai 200092,China)
In this paper,with cost optimization as the objective,we considered such constraints as finite workshop resources,etc.,and then explored the application of the Kanban-based milk-run distribution practice in the distribution system of the logistics supermarket.
Kanban;logistics supermarket;mixed-flow assembly line;cost optimization
F426.471;TH165.1
A
1005-152X(2015)10-0225-03
2015-07-25
丁佳祺(1990-),女,江苏苏州人,同济大学经济与管理学院硕士研究生,研究方向:物流管理;张镓(1975-),男,天津人,同济大学经济与管理学院博士研究生,研究方向:物流与供应链管理;蔡三发(1973-),男,福建长泰人,同济大学经济与管理学院研究员,研究方向:物流与供应链管理。
10.3969/j.issn.1005-152X.2015.10.060

