雷击大地年平均密度Ng取值方法的探讨*
石湘波 胡余斌 郑玲 王焕邦
(宁波市防雷中心, 浙江 宁波 315012)
防雷减灾
雷击大地年平均密度Ng取值方法的探讨*
石湘波 胡余斌 郑玲 王焕邦
(宁波市防雷中心, 浙江 宁波 315012)
雷击大地年平均密度Ng是雷击风险评估中的重要参数。首先,通过对目前普遍使用的多年平均雷暴日Td计算Ng、应用网格法或圆面积法计算Ng以及应用Topsis法计算Ng等3种方法的分析,发现这些方法的计算出的Ng值存在精细化程度较低及不符合地闪实际分布情况等不足。其次,以宁波地区为例,从雷击风险概率角度,在计算得出本地区雷电流幅值累积分布概率表达式的基础上,提出基于雷击风险概率的圆面积法来计算Ng值。最后,通过应用上述4种方法计算宁波地区3个国家基本气象站的Ng值并进行比较分析,对4种方法的适用性进行了进一步验证和说明。
雷击大地年平均密度;雷击风险概率;圆面积法;雷电流幅值累积概率
0 引 言
在雷击风险评估中,雷击大地年平均密度Ng是一个非常重要的参数。Ng值的正确与否,将直接影响雷击风险评估结果的准确性和可靠性。
IEC在2006年正式发布的IEC62305-2《雷电防护第二部分:风险管理》及GB50057-2010国家标准中,都提出了关于Ng取值方法。目前针对Ng的取值方法主要有以下3种:第一种是在没有地闪数据可以使用的情况下,则采用多年平均雷暴日Td,使用IEC及GB规范内相关公式来计算Ng;第二种是利用闪电定位系统测定的地闪数据来计算;第三种则是引入时间权重为区间值的时间序列多指标决策Topsis方法,利用多年平均雷暴日和闪电定位系统测得的地闪数据来计算Ng值。
在实际雷击风险评估工作中,发现应用上述3种方法计算得出的Ng值差异较大,影响评估中后续数据计算值的可靠性。为解决这些问题,本文通过对3种计算Ng值的方法进行比较分析,用以充分了解、判别所述方法的适用性、可靠性和局限性,并提出新的改进方法弥补缺陷。
1 3种常见Ng取值方法的分析
1.1 应用多年平均雷暴日Td计算Ng

不少地区防雷工作者经常依据上述这些规范提供的公式进行计算,但并不知道这些公式在计算本地区的Ng值是否准确。IEC和GB规范中都提到这种方法存在局限性:即在无法取得地闪数据的情况下,可以使用该方法。下面就具体分析一下其存在的局限性:首先,从数值的取值方法来说,雷暴日与地闪密度并无直接联系;因为雷暴日资料的取得来源于各地气象台站的人工观测数据,其统计方法为通过人工观测来确定,一天之内只要听到或看到一次或一次以上雷声或闪电,均记为一个雷暴日[3]。因此雷暴日是不区分云闪和地闪的,虞昊[4]等经过大量观测统计发现云闪次数是地闪次数数倍,而且与纬度负相关。因此无论从实际监测的还是从理论上来说雷暴日数必然大于闪电定位系统测定有地闪的日数。也就是统计雷暴日Td还涉及到云闪,而Ng是只是由地闪数据得出的雷击大地密度,因此据此建立的Ng与Td的关系式所得数值各个地区不可能相同。其次,一个地市级的行政区域24 h有人值守国家基本气象站一般在2~3个左右,且人工观测范围在8~15 km[5],气象站监测范围无法覆盖整个区域,因此观测到雷暴日数无法代表整个区域的雷暴日发生情况。最后,应用这些站点的多年雷暴日资料来计算整个地区的Ng值,同样也是没有实际使用价值的。因为根据这些站点计算得出的Ng值,只能代表人工观测范围内的雷击大地密度,而不能说明该地区其他区域的雷击大地密度均为该值,且一个地区也不可能只有2~3个雷击大地的密度值。
鉴于这些存在的局限性,在实际防雷工作中,尽量避免使用年平均雷暴日来计算年平均雷击大地密度。
1.2 根据闪电定位数据来计算Ng
目前国内绝大部分地区都布置了闪电定位仪,地闪数据也得到了广泛的应用。目前应用地闪数据来计算雷击大地密度主要有网格法和圆面积区域法。网格法的基本原理是对研究区域进行均匀连续的网格划分,设定每个网格为一个统计单元,以统计每个单元网格内的雷电参数,选择合适的网格大小可提高雷电参数统计值的准确性。陈家宏等[6]通过统计和对比分析福建13 a气象雷电资料和5 a雷电定位系统监测数据,得出福建取0.15°×0.15°网格来统计雷电参数。尹丽云等[7]通过滇中地区1987—2006年49个气象站的人工观测资料和2005—2006年闪电定位资料的对比分析,采用等面积数据源统计,得出滇中地区取0.175°×0.175°网格来统计雷电参数。当前普遍通行的确定网格大小的方法是通过应用人工观测雷暴日来确定的。圆面积区域法的原理是以分析对象为中心,选定半径r的圆面积S,计算得出圆内的地闪密度以代表分析对象的地闪密度。余海军等[8]利用1999—2008年广东省雷暴日和LLS资料应用圆面积区域法对广东省多个气象站的人工雷暴日与多种半径圆面积内雷电日进行对比分析,得出半径为7 km的圆内的雷电日与人工雷暴日数相关性较高,并计算得出相应的地闪密度。这些方法虽然也存在人工站点少的问题,但精细化程度较应用Td公式计算Ng值要高很多。从上可以看出网格大小划分必须要有依据,同样圆半径大小的取值也是同样要求,但由于这些网格划分较大无满足防雷工作精细化的要求,有些防雷工作者为片面追求Ng精细化高的需求,随意缩小网格尺寸或半径大小,那这样得出的数据很难说是可靠的。
网格法和圆面积区域法虽然提高了精细化程度但还存在不足:首先,用网格法来划分,按照人工雷暴日确定网格大小一般都在十几公里×十几公里左右,一个地市级行政区域一般只能够划分出十几个或二十几个网格,那么在网格内各处雷电参数无任何差异,也就是说网格中心与边缘的雷电参数相同,这不符合实际情况;其次,圆面积区域法由于确定其半径大小也与人工雷暴日相关,因此只适合于有国家基本气象站的区域,而且只适合以气象站为中心的区域,这样其适用范围受到很大限制。
1.3 应用Topsis法计算Ng
Topsis法就是将1.1和1.2两种方法取得的Ng值代入时序多指标决策Topsis中的时间权重法[9]其公式为:
(1)
其中Ng1为Ng通过与Td的关系式计算得出的值
Ng2为利用闪电定位数据所计算的值
T1是以年为单位的人工观测雷暴日资料的时间
T2是以年为单位的闪电定位资料的时间
由于人工观测的雷暴日资料一般时间长度都在40 a以上,而闪电定位网建立也只不过只有区区几年,雷暴日资料所占时间权重大,因此依照Topsis法计算所得的Ng值,必然和通过Td的关系式计算得出的Ng值很接近,同样这也不能解决整个较大面积区域所需精细化的Ng值的问题。
2 基于雷击风险概率的圆面积法
鉴于上述3种方法中出现的不足和局限性,针对雷击风险评估的实际要求,基于对电子设备和人的雷击风险防护,提出基于雷击风险概率的圆面积法。
在雷击风险评估中,Ng值主要用于计算以下几方面:1)建筑物的年预计雷击次数;2)邻近建筑物的年预计雷击次数;3)雷击建筑物附近的年预计雷击次数;4)雷击服务设施线路的年预计雷击次数;5)雷击入户服务设施线路附近的年预计雷击次数。其主要目的是评估人或电子设备可能遭受雷击损害或失效的风险。雷击大地也就是地闪,是造成地面人或物损害的原因。人或电子设备被雷电直接击中或距离雷击点极近,都会造成伤亡或损坏。雷击对建筑物内及建筑物附近人员的影响也只存在于直接雷击或近距离损害,而一定距离以外发生的地闪则对人体基本无害,但对电子设备有可能还存在影响甚至造成损害。因为对于电子设备来说,发生雷击时,强大的雷电流及其所产生的空间电磁脉冲主要通过传导、感应和耦合等方式对电子设备产生各种暂态过电压。考虑到涉及一般建筑的长距离传输线路主要为电源和通信两种线路,由于雷击风险评估阶段,线路的铺设方式、长度及走向都是未知情况,因此对于长距离传输线路上的雷电流传导、感应和耦合对电子设备的影响暂不做考虑。这里主要以建筑物内及附近的电子设备及线路作为分析对象,电子设备中所采用的大量半导体器件和集成电路,由雷击产生的暂态电磁脉冲会通过辐射的形式影响这些元器件也可以在电源或信号线路上感应出暂态过电压,沿线路侵入电子设备,使设备工作失灵或损坏。因此,在远距离传输线路未知的情况下,由雷击产生的暂态电磁脉冲使其附近一定范围内的未采取防雷措施的电子设备受到干扰和损坏,其辐射的影响范围是最广的。
电子设备中以计算机应用最为广泛,且具有代表性。根据国外进行的模拟实验表明[10],在不加屏蔽的情况下,使计算机失效的脉冲磁感应强度Bf=0.07×10-4T,使计算机元器件损坏的脉冲磁感应强度Bd=2.4×10-4T。脉冲磁感应强度与雷电流幅值直接相关,雷电主放电形成的最大脉冲磁感应强度公式可以表达为:
(2)
上式中Im为雷电流幅值(kA),r为计算机到雷击大地点的水平距离(km),系数k为7.96×105。
从公式(2)可以看出,在不加屏蔽且雷电流幅值一定的情况下,离雷击大地点越远,脉冲磁感应强度B就越小,电子设备受影响的可能也就越小。根据闪电定位系统统计发现,每个地闪雷电流幅值和发生位置都不同。我们不可能了解每一个地闪对电子设备是否造成影响,但我们可以计算地闪的雷电流幅值对电子设备造成影响的概率,某一次产生超过损害或失效阈值脉冲磁感应强度的地闪,在某个范围内,对电子设备造成失效和损害的概率是100%,但这一范围内的地闪的雷电流幅值大小不一,发生位置不同,产生脉冲磁感应强度也不同,对设备造成的影响也不同,也就是可能不造成损害和失效的影响。因此,可以通过计算一定范围内的可能对电子设备造成损害或失效的雷电流幅值出现的概率,来了解电子设备的损害或失效的概率。
要了解这个概率,那分析雷电流幅值累积分布概率就成为关键。雷电流幅值是雷电流的一个重要参数,指脉冲电流所能达到的最大值,也就是每个地闪的强度,其值大小不一。因此对其累积概率的统计、分析十分有必要。通过对某个地区的雷电流幅值累积概率进行分析研究,能更好地了解该地区的雷电特性,分析雷灾原因,鉴定雷电跳闸事故,提供雷击风险评估参数依据等。
由于雷电流幅值变化范围较广,存在多种表达式。目前我国普遍推荐采用电力行业规程《交流电气装置的过电压保护和绝缘配合》(DL/T620-1997)中的公式,即lgPI=-I/88。雷电流幅值的大小与较多因素有关, 各地幅值概率分布有较大差别,因此国内外使用的雷电流幅值概率分布表达式并不统一,很多学者[11-13]根据各地实际情况,归纳出各自地区相应的雷电流幅值累积概率表达式。利用宁波市雷电流幅值数据, 分析宁波市雷电流幅值累积概率分布情况, 将宁波市的雷电流幅值累积概率分布统计曲线与我国的雷电流幅值累积概率经验公式比较(见图1)。从图1可以看到,宁波市雷电流幅值的累积概率曲线与我国经验曲线分布趋势是一致的, 都是随着雷电流幅值的增大而递减, 但是两者有一定区别。在22 kA以下的雷电流幅值概率累积中,宁波市的曲线更陡,变化较大,而国家经验曲线相对较平缓, 变化相对较小,表明宁波市雷电流幅值在22 kA以下的累积概率与国家相差较大;雷电流幅值大于22 kA两者的变化正好相反;雷电流幅值大于120 kA,两条曲线都显示累积概率较小,且基本重合,表明120 kA以上雷电流幅值的累积概率,宁波市的情况和国家经验公式基本一致。

图1 宁波市雷电流幅值累积概率曲线与通用经验累积概率曲线比较
为了能更好地拟合分析, 采用最小二乘法,通过指数和多项式拟合, 添加两种趋势线(见图2),并用调整后的相关系数R来反映拟合曲线与原曲线之间的拟合程度。

图2 宁波市雷电流幅值的统计与拟合图
利用指数拟合得到的公式为PI=138.75e-0.04I,R=0.98139,多项式拟合的结果为PI=128.8-4.3I+0.05I2-2.85×10-4I3,R=0.94132。
通过比较指数拟合的结果与多项式拟合的结果,可以发现指数拟合相关系数R大于多项式拟合时的值,说明用指数进行拟合时与实际统计曲线相关性更高,产生的误差更小,因此用指数拟合曲线来代表原数据曲线更加合理,得出宁波市雷电流幅值累积概率分布表达式:
PI=138.75e-0.04I
(3)
不发生的概率应该为零,那这个r将为无穷大,这就没有计算的意义了。在统计学上来看,0.01~0.005为小概率事件,事件发生概率在0.01或0.005以下的时间成为小概率事件,0.01和0.005这两个值成为小概率标准[14]。小概率事件是指发生概率极小的,只存在理论上发生的可能,实际情况下,一般不太可能会发生的事件。0.01~0.005取值越小相应距离就越远,为考虑参数精细化,因此设定在一定范围r外,出现使电子设备有可能失效或损坏的地闪概率在0.01以下。根据公式(2)、(3)计算r公里以外使电子设备失效的地闪出现概率低于0.01:
Pf(r)=138.75e-0.04×2πrBf
Pf(r)≤0.01
计算得:r≥7 km
由计算结果可知半径7 km以外区域发生的地闪对电子设备的失效影响概率在0.01以下,对电子设备造成的影响极小可以近似忽略。
Pd(r)=138.75e-0.04×2πrBd
Pd(r)≤0.01
计算得:r≥2 km
由计算结果可知半径2 km以外区域发生的地闪对电子设备的损害影响概率在0.01以下,对电子设备造成的损害概率极小可以近似忽略。
从上述计算可知,距离电子设备7 km以外的地闪造成电子设备失效概率在0.01以下,造成电子设备的损害概率则更低,可以忽略考虑7 km以外发生的地闪对电子设备所造成的影响。反之,则是7 km以内发生的地闪造成电子设备失效和损害的概率相对较高,因此不能忽略7 km范围以内的地闪。可通过计算电子设备7 km范围内的地闪分布情况,根据圆面积区域法计算得出电子设备所处区域的Ng值。该方法优点在于可不受分析对象所处位置限制,即可随分析对象位置不同而得出不同的地闪数据,差异化和精细化程度得到提高,且取值依据明确。
3 4种方法应用计算结果分析比较
为进一步分析多年平均雷暴日Td计算Ng法、应用网格法或圆面积法计算Ng法以及应用Topsis法计算Ng法与基于雷击风险概率的圆面积法在计算Ng的适用性和局限性,选取宁波地区3个国家基本气象站,分别为鄞州站(121.55°E,29.783°N)、石浦站(121.95°E,29.2°N),慈溪站(121.267°E,30.2°N),采用1971—2013年43 a人工气象观测资料和2010—2013年闪电定位资料,应用4种方法,以各个气象站为分析对象,计算气象站Ng值。其中根据2010—2013年闪电定位资料和相应年数的雷暴日资料,分析比对发现半径为8 km的圆面积和14 km×14 km网格比较符合宁波实际情况。根据4种方法计算Ng结果见表1。
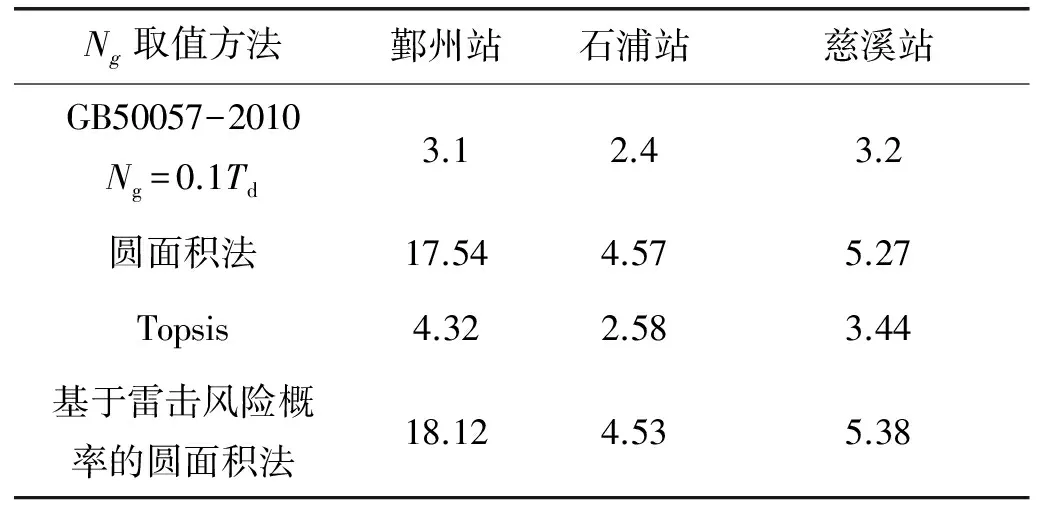
表1 4种方法计算宁波3个国家基本站Ng值 次/km2·a
从上述4种方法的计算结果来看。规范中的应用多年平均雷暴日Td计算得出的Ng值明显小于其他方法计算的Ng值,经过3个站点地闪密度数据比较发现,在地闪密度较低的站点(石浦站和慈溪站)应用四种方法计算出的地闪密度值差异相对较小,而在地闪密度较高的站点(鄞州站),从表中可以看出差异巨大。因此规范中应用Td计算Ng的方法,在无法取得闪电数据情况下,在雷暴活动较少的地区可能较为适合,而在雷暴活动频繁的地区该公式明显不适用,且更不能用于表征较大面积的地区级行政区域的Ng值。Topsis法计算所得的Ng值也因为算法原因,数值较为接近应用Td计算的Ng值。网格法与圆面积法和基于雷击风险概率的圆面积法用于计算Ng都比较接近于实际情况,网格法一般用于表达整个地区较大范围的地闪密度分布情况,但网格内的雷电参数精细化程度不够;圆面积法则因需要与人工雷暴日资料对应而受到使用范围的限制;而基于雷击风险概率的圆面积法则更适合于对单个评估对象的周围地闪密度情况的分析,而且不受任何地点和区域限制。
4 结 语
通过对应用多年平均雷暴日Td计算Ng、应用网格法或圆面积法计算Ng以及应用Topsis法计算Ng等3种方法的分析,并从雷击风险概率角度,在分析得出本地区雷电流幅值累积分布概率表达式的基础上,提出新的圆面积法来计算Ng值;最后根据宁波地区3个国家基本气象站1971-2013年人工雷暴日资料以及2010-2013年闪电定位资料,应用上述四种方法计算得出Ng并进行对照分析,得出如下结论。
1)IEC以及GB规范中应用Td计算Ng的方法,在无法取得闪电数据情况下,在雷暴活动较少的地区可能较为适合,而在雷暴活动频繁的地区该公式明显不适用,且更不能用于表征较大面积的地区级行政区域的Ng值。Topsis法计算所得的Ng值也因为算法原因,数值较为接近应用Td计算的Ng值。
2)网格法与圆面积法用于计算Ng较应用Td计算Ng的方法的精细化程度要提高许多,网格法一般用于表达整个地区较大范围的地闪密度分布情况,但网格内的雷电参数精细化程度不够;圆面积法则因需要与人工雷暴日资料对应而受到使用范围的限制;
3) 基于雷击风险概率的圆面积法,其半径大小取自电子设备受影响范围,适合于对单个雷击评估对象的周围地闪密度情况的分析,而且不受任何地点和区域限制。
[1] 马金福,冯志伟.雷击地闪密度与雷暴日数的关系分析[J].气象科学,2009,29(5):674-678.
[2] 钟颖颖,冯民学,周曾奎,等.闪电定位资料与目测雷暴日的对比分析[J].气象科学.2010,30(8):851-855.
[3] 中国气象局.地面气象观测规范[M].北京:气象出版社,2009.
[4] 虞昊,庚媛,张勋文,等.现代防雷技术基础[M].北京:清华大学出版社,1995.
[5] Gary R.Huffines , Richard E Orville . Lightning Ground Flash Density and Thunderstorm Duration in the Continental United States: 1989-96 . Journal Of Applied Meteorology . JULY1999.1013-1019.
[6] 陈家宏,郑家松,冯万兴,等.雷电日统计方法[J].高电压技术,2006,32(11):115-118.
[7] 尹丽云,许迎杰,张腾飞,等.一种新的雷电日及雷电参数统计方法[J].气象科技,2009,37(6):739-743.
[8] 余海军,陈水明,朱建军,等.雷电定位系统监测雷电日与人工记录雷电日的比较[J].高电压技术,2012,38(10):2742-2748.
[9] 高燚,劳小青,李健生,等.雷击风险评估中雷击大地年平均密度的计算[J].气象研究与应用2009,30(3):68-70.
[10] 张小青.建筑物内电子设备的防雷保护[M].北京:电子工业出版社,2000.
[11] 李家启,王劲松,申双和,李博,陈宏,林涛.基于ADTD系统监测的雷电流幅值累积概率特征分析[J].气象,2011,37(2):226-231.
[12] 陈家宏,童雪芳,谷山强,李晓岚.雷电定位系统测量的雷电流幅值分布特征[J].高电压技术,2008,34(9).
[13] 李瑞芳,吴广宁,曹晓斌,马御棠,刘平,苏杰.雷电流幅值概率计算公式[J].电工技术学报,2011(4):161-167.
[14] 浙江大学.概率论与数理统计.北京:高等教育出版社,2010.
2014-07-14
*资助项目:宁波市气象局科技计划项目(NBQX2012010B)

