基于FPGA的五电平逆变器SVPWM算法的实现

谭维胜， 王 辉， 黄 庆， 潘小清

(湖南大学电气与信息工程学院，湖南长沙 410082)

基于FPGA的五电平逆变器SVPWM算法的实现

谭维胜， 王 辉， 黄 庆， 潘小清

(湖南大学电气与信息工程学院，湖南长沙 410082)

介绍了一种新型的五电平逆变器电压空间矢量脉宽调制(SVPWM)算法，该算法中不含复杂的三角函数运算，因此便于利用FPGA实现。设计了一种基于DSP和FPGA的硬件控制电路，其中FPGA主要用于实现SVPWM算法。给出了该算法利用FPGA实现的具体方法和步骤，并且利用Quartus II软件对该算法进行了仿真和实验验证。仿真和实验结果与理论计算相符，验证了本设计是正确且有效的。

空间矢量脉宽调制(SVPWM)；五电平逆变器；FPGA

近年来，在中、高压大容量变频调速器和电力有源滤波器大量应用的促使下，多电平逆变器已成为当前电力电子技术中备受人们关注的重要研究热点，受到了社会的广泛关注。

对于电平数大于3的多电平逆变器，通常其需要的PWM控制信号大于12路，如本文所用到的中点箝位H桥五电平逆变器需要24路PWM控制信号。因此单独使用DSP芯片已经不能够满足控制要求，目前国内外学者多采用DSP+FPGA的结构来实现多电平逆变器的控制[1-2]。本文也采用DSP+FPGA这种控制系统电路结构，其中FPGA主要用于实现五电平逆变器SVPWM调制算法。本文使用了一种新型的SVPWM算法来实现中点箝位H桥五电平逆变器PWM调制，该算法能够有效地消除矢量突变，且不含复杂的三角函数运算[3]。由于FPGA具有设计灵活、开发周期短、可靠性高、纯硬件并行处理等优势[4-5]，因此本文采用FPGA来实现五电平逆变器SVPWM算法。

1 五电平逆变器的拓扑结构及其工作原理

本文中五电平逆变器的拓扑结构为中点箝位H桥五电平电压型逆变器，其拓扑电路如图1所示。

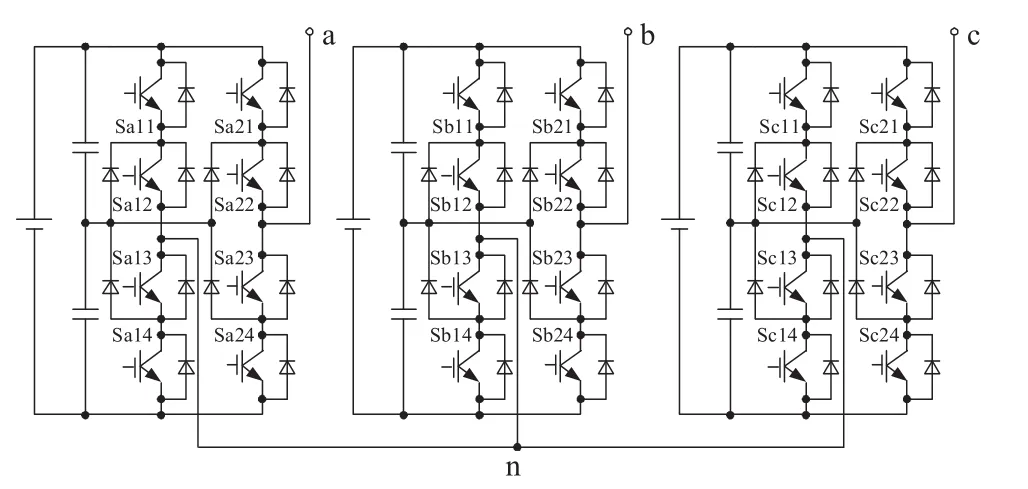
图1 中点箝位五电平H桥逆变器的拓扑结构

从图1可以看出中点箝位H桥五电平逆变器是由三个3H桥构成，每相可以输出-2E、-E、0、E、2E五种电平(其中E为dc/2，dc为直流端电压)，3H桥输出的五种电平与各个开关器件的关系如表1所示。常规的五电平逆变器输出的五种电平为dc/2、dc/4、0、-dc/4、-dc/2，因此这种拓扑结构与常规的五电平逆变器相比，在直流母线电压相同的情况下可以获得更高的输出电压。

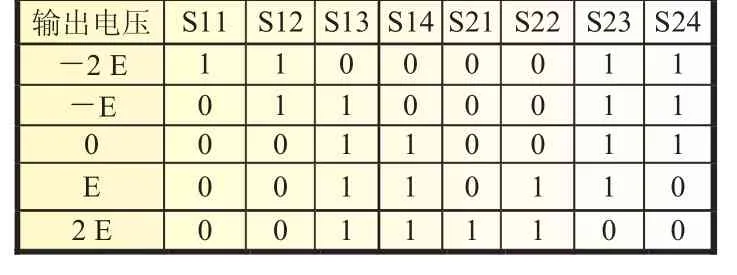
表1 3H桥输出五种电平时各个开关的状态

2 硬件控制电路设计

本文采用DSP+FPGA这种结构作为控制系统电路，其中FPGA主要用于实现SVPWM调制算法。通常在SVPWM算法中，其输入信号为采样时间s，直流母线电压dc以及参考电压(refα，refβ)，这些信号均由DSP经数据总线发送给FPGA。DSP和FPGA通过地址总线、数据总线以及控制总线相互连接，其接口电路如图2所示。

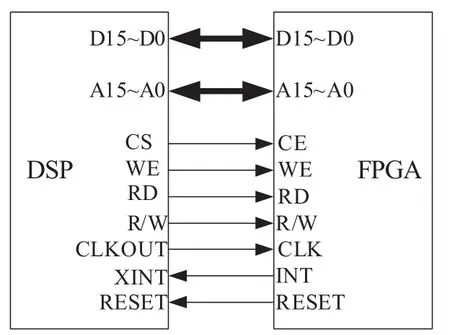
图2 DSP与FPGA接口电路

图2中的DSP和FPGA接口电路可以实现双向数据传输，控制总线中CS为选通信号，其有效表示与FPGA进行通信；WE、RD、R/W分别为写信号、读信号和读写选择信号；DSP的CLKOUT与FPGA进行连接可用于为FPGA提供同步时钟信号；另外DSP还可响应来自FPGA的外部中断以及可通过FPGA对DSP进行复位操作。

3SVPWM算法及其FPGA实现

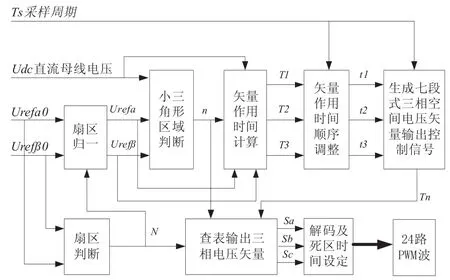
图3 五电平逆变器SVPWM算法实现框图

五电平逆变器SVPWM算法主要包括扇区判断模块、扇区归一模块、小三角形区域判断模块、矢量作用时间计算模块，输出电压矢量控制信号生成模块、三相电压矢量输出模块等。五电平逆变器SVPWM算法实现框图如图3所示，下面将分别介绍各个模块的原理及其FPGA实现，这些算法全部利用VHDL语言实现。

3.1 扇区判断和扇区归一

要实现SVPWM调制，首先要判断出参考电压所在的扇区。扇区的判断是根据3条规则来确定的，这3条规则及其与各扇区的对应关系如表2所示。

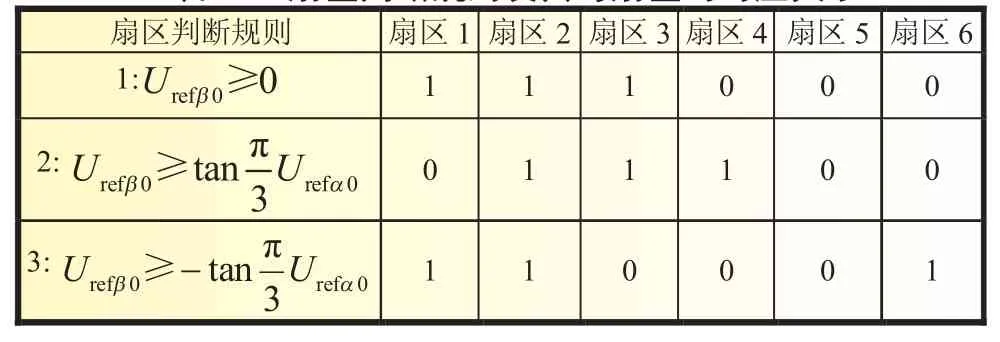
表2 扇区判断规则及其与扇区的对应关系

由表2可以看出，根据参考电压的值可以很轻松地判断出参考电压所在扇区。判断出参考电压ref0所在扇区后，再进行扇区旋转归一，扇区旋转归一公式如下：

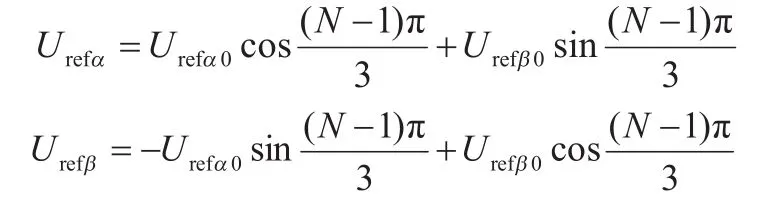
当参考电压不是位于第1扇区时，通过利用上述公式进行归一化处理，在接下来的小三角形区域判断及时间计算都可以将其当作位于第1扇区来进行处理，这样可以大大简化计算。

利用VHDL语言容易编程实现扇区判断和扇区归一，编程设置三个比较器，通过三个比较器的输出值可以很容易判断出参考电压所在扇区。判断出参考电压所在扇区后，就可以将参考电压进行归一化处理，虽然在归一化处理中含有三角函数运算，但是由于角度值为常数，所以三角函数值也为定值。这其中涉及到小数运算，为了不给FPGA带来太大的负担，采用先乘后除的方法来表示小数，如可用1 732/1 000来代替。当其他值与相乘时，为了提高计算进度可将除以1 000放在最后。

3.2 小三角形区域判断

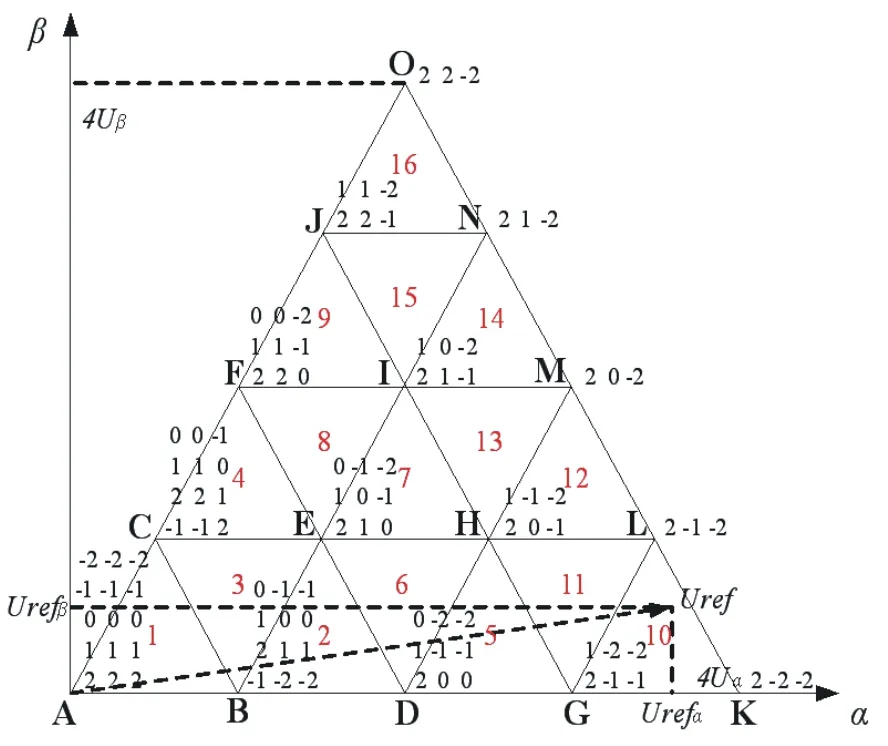
图4 五电平逆变器第一扇区的空间矢量图

五电平逆变器位于第一扇区的空间电压矢量图如图4所示，从五电平逆变器的空间电压矢量图中可以看出其每个扇区都含有16个小三角形区域。本文中小三角形区域的判断采用文献[3]中所述方法，即利用十二条规则来判断参考电压所在位置，文献[3]中还给出了16个小三角形区域与这十二条规则的对应关系。

小三角形区域判断的FPGA实现与扇区判断相同，只需根据十二条规则设置相应个数的比较器。根据比较器的输出值即可得到这十二条规则的真伪，然后再根据这十二条规则与小三角形区域的对应关系判断出参考电压所在小三角形区域。

3.3 矢量作用时间的计算

每一次采样所得到的参考电压必定落在某一个小三角形区域中，而每个小三角形的三个顶点对应着三个不同的矢量，参考电压便可以由这三个矢量合成。合成原则由伏秒平衡公式给出，伏秒平衡公式如下：

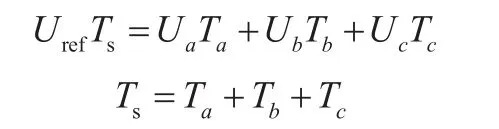
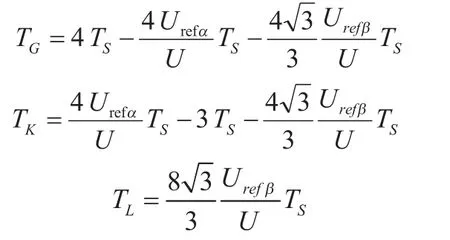
假设参考电压落在10号小三角形区域中，由伏秒平衡公式可计算出三矢量作用时间分别为：式中：=2dc/3。当参考电压落在其他小三角形区域时也可以根据伏秒平衡公式计算出各矢量的作用时间。

在用VHDL语言实现矢量作用时间计算中，要先辨别参考电压所在的小三角区域号的值，然后再根据的值选择相应的公式计算出a、b、c的值。在计算中为了提高计算精度，一般将除法放在最后，但是在前面的乘法计算中有可能超出integer的数值范围(-231～231)，所以要根据参考电压的值来对除的位置做相应的调整。

3.4 七段式三相电压矢量输出控制信号的生成

本文采用七段式矢量输出作用顺序，两相邻三角形矢量输出顺序采用正反循环的方法，起始矢量采用小三角形中编号最小的那个矢量。七段式矢量输出中各段作用时间分别为/3-/2-/2-/3-/2-/2-/3(扇区号为奇数)或/3-/2-/2-/3-/2-/2-/3(扇区号为偶数)。

在FPGA中，为了简化设计，调制波采用锯齿波，如此则只需加计数。用VHDL语言设计一个加法计数器，从0计到20 833，在每一个基准时钟的上升沿来临时计数器加1，且不断地与三矢量作用时间进行比较，将三矢量作用时间a、b、c分为7段，生成范围为1到7的七段式矢量输出控制信号n。七段式矢量输出控制信号n的每一个值的时间长度对应相应电压矢量的作用时间(n与七段式输出适量的对应关系如图5所示)。为了实现FPGA与DSP同步，在DSP每次发送新的参考电压数据给FPGA的同时，将计数器清零。

3.5 三相电压矢量的输出

三相电压矢量的输出是根据前面计算出来的扇区N、小三角型区域n以及三相矢量输出控制信号Tn的值，利用case语句来选择所要输出的三相电压矢量。得到三相电压矢量后，再加上解码和死区时间控制就可以得到24路PWM波信号。

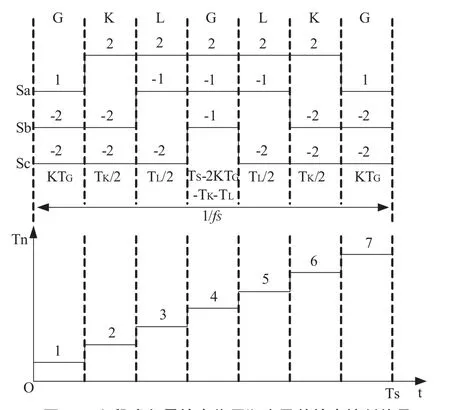
图5 七段式矢量输出作用顺序及其输出控制信号

4 仿真和实验结果

为了验证本文中所述五电平逆变器SVPWM算法的正确性，本文在Quartus II 9.0软件环境下利用VHDL语言对SVPWM算法中各模块进行了编程及编译仿真。仿真结果如图6所示。为了更直观地表明仿真结果的正确性，没有直接给出24路PWM信号波形，而是给出了三相电压矢量Sa、Sb、Sc，扇区号N，小三角形区域号n等。

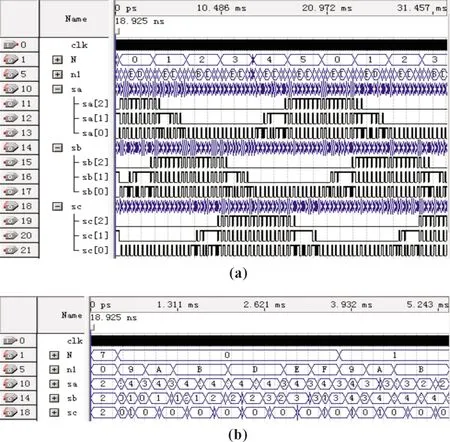
图6 三相电压矢量仿真结果

从图6(a)中给出的40 ms的三相电压矢量可以看出三相矢量输出信号Sa、Sb、Sc相位相差120°，且按一定规律变化，变化周期为20 ms，与给定参考电压的频率50 Hz相符；扇区从0变化到5，分别对应1到6扇区。另外从图6(b)中可以看出，在每一个扇区中，其对应输出的小三角形编号分别为9、A、B、D、E、F(分别对应图1中的10、11、12、14、15、16)，通过这些小三角形区域编号对应时间的长短，我们可以判断出在每一扇区采样的8个数据，落在9、A、E、F区域的各有1个数据，而B、D区域则各包含有2个数据。通过以上分析，可以断定仿真结果是正确的。

为了进一步验证本设计的正确性，本文将利用VHDL语言编写的SVPWM算法程序下载到FPGA实验板中进行了实验，实验结果如图7所示。实验所采用的FPGA芯片为A1tera公司的cycloneⅡ系列FPGA EP2C8Q208C8，该芯片拥有8 000多个逻辑单元，完全能够满足实验要求。图7给出的为A相矢量Sa输出结果，通过与图6(a)的仿真结果进行比较可以看出仿真和实验结果基本一致。

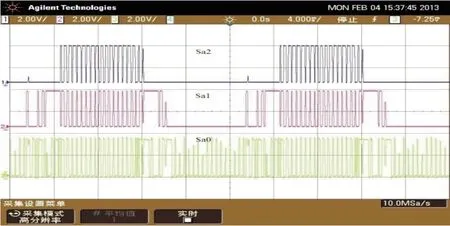
图7 实验结果

5 结论

本文介绍了一种新型的五电平逆变器的SVPWM算法，该算法通过优化七段式矢量作用次序以实现有效地消除矢量突变，且不含复杂的三角函数运算，所以便于硬件实现。本文采用FPGA来实现该算法，并利用Quartus II软件和VHDL语言对该算法进行了编程和仿真，并最终将通过编译的程序下载到A1tera公司的cycloneⅡ系列FPGA EP2C8Q208C8芯片进行实验。仿真和实验所得到的结果与理论分析相符，验证了本文SVPWM算法的正确性，同时也表明本文采用FPGA实现该SVPWM算法是可行的。

[1]何国军，陈维荣，刘小强，等．基于DSP与FPGA的运动控制器设计[J]．电子技术应用，2009，39(7)：35-37．

[2]任晶，夏加宽，沈丽．基于DSP和FPGA的多相变频控制器的设计与实现术[J]．电子技术应用，2012，38(3)：23-26．

[3]王辉，谭维胜，瞿超杰．中点钳位H桥五电平逆变器空间矢量脉宽调制方法研究[J]．湖南大学学报：自然科学版，2012，39 (4)：42-47．

[4]祁超，王庆章，赵耀，等．基于FPGA的三相SVPWM调制算法的实现[J]．南开大学学报：自然科学版，2011，44(4)：26-30．

[5]朱洪顺，符晓，戴鹏．基于FPGA的三电平SVPWM新型算法的实现[J]．电气传动，2011，41(11)：29-31．

Implement of five-level inverter SVPWM algorithm based on FPGA

A novel algorithm of space vector pulse width modulation(SVPWM)for five-level inverter,without contain complex trigonometric function calculation,was introduced.Then FPGA was used.A control circuit based on DSP and FPGA was designed,and the FPGA was used to implement the SVPWM algorithm.The implementation approachs and concrete steps for the algorithm by used of FPGA were given,and the Quartus II software was used to simulated and experimental for the algorithm.The simulation and experimental results were consistent with the theoretical calculation,it showed that the design was correct and effective.

space vector pulse width mdulation(SVPWM);five-level inverter;FPGA

TM 464

A

1002-087 X(2015)10-2240-04

2015-03-17

国家国际科技合作项目(2011DFA62240)；湖南省国际科技合作项目(2011WK2012)

谭维胜(1987—)，男，湖南省人，硕士生，主要研究方向为电力电子与电力传动。