基于低秩鉴别投影的轴承故障特征提取方法

梁礼明，吴武林，吴健

(江西理工大学 电气工程与自动化学院，江西 赣州 341000)

滚动轴承的峰值因子、峭度、脉冲因子等时域参数，频域频谱特征和能量等包含了丰富的轴承运行状态信息，因此可以提取这些参数作为故障诊断的高维特征[1]，但得到的高维特征空间中不可避免地存在一些与故障诊断不相关的特征和冗余特征，不利于故障诊断，因此需要提取高维特征空间中的低维特征。主成分分析(Principal Component Analysis，PCA)仅能有效地发现全局欧式结构，因而无法发现隐藏在数据中内在的非线性流形结构。为了发现位于轴承数据空间中的内在流形结构，文献[2]等利用流形学习的方法提取故障信息，取得了不错的效果。流形学习方法是以数据最近邻域的个数和本质维数或降维维数已知为前提，降维效果严重依赖于对这些参数的选择，但目前流形学习中最近邻域的个数和本质维数如何确定是一个有待研究的问题，而且它们是定义在训练样本上的，还不能有效处理新测试样本。

针对流形学习面临的上述问题，提出了基于低秩鉴别投影的轴承故障特征提取方法。低秩表示同时考虑到类间的差异性和类内的同一性，因而能准确描述数据的全局结构，低秩鉴别投影算法拥有低秩表示的良好数据全局结构表达能力和一定的判别结构表达能力[3]，并且能够得到显示的投影矩阵，泛化能力强。

1 低秩鉴别投影

1.1 低秩表示的基本思想

假设训练数据样本由X=[x1,x2,…,xn]构成，低秩表示[3-5]的目的是寻求训练集中每一个独立的数据向量作为所有数据向量的线性组合表示，考虑到实际数据采集过程中的噪声干扰，低秩表示模型可以表示为

(1)

式中：W为系数矩阵;‖W‖*为矩阵W的核范数，即该矩阵奇异值之和；参数a>0；E2,1为噪声矩阵的l2,1范数，用来描述噪声的类型，在此用来模型化受大噪声干扰的样本。(1)式的最优解可利用非精确增广拉格朗日乘子法求解[6]。

1.2 低秩鉴别投影算法

低秩鉴别投影算法[7-8]的思想是：首先求出(1)式的最优解W并将其分解为类内表示、类间表示和噪声3个部分；然后尽量使类间散度足够大，类内散度和噪声散度足够小；最后寻找一个投影矩阵，使数据经过线性投影后的低秩结构保持不变，且低维空间聚类效果更好。

(2)

假设经过线性转换后低秩结构保持不变，则

y=PTx，

(3)

(4)

式中：P为投影矩阵。

在变换空间中，类内散度可描述为

(5)

其中类内散度矩阵为

(6)

类间散度可以描述为

(7)

其中类间散度矩阵为

同时，为了使数据更好的分布，希望投影后的噪声越小越好，因此要使(4)式中PTei,j的范数最小化，即

(9)

X(I-W)(I-W)TXT。

(10)

则最优投影的判别准则为

(11)

式中：I为单位矩阵；r为组合参数，用于平衡类内散度与噪声散度。为了更容易地估计参数，简便计算，定义一个联合矩阵，令

(12)

判别准则转化为

(13)

低秩鉴别投影算法步骤为：

1)给定c类数据集X，用非精确增广拉格朗日乘子法计算最优相似矩阵W。

2 基于低秩鉴别投影的故障特征提取方法

2.1 高维特征空间构建

将上述时域特征和频域特征组成N×D的故障诊断高维特征空间。每种轴承状态数据抽取50 组样本，则全体状态样本数N=200；高维特征数D=16。每种状态下抽取25组样本作为训练样本D1，其余的作为测试样本D2。

2.2 参数a和r的确定

2.3 稀疏表示分类器

信号的稀疏表示[9-10](Sparse Representation)是指将信号在特定的原子库中进行分解，如果原子库中的原子与信号的主要成分相似，则仅需要少数原子的线性组合就能很好地逼近原始信号。

选取y中第i类别的训练样本为Ai=[ai1,ai2,…,ain]∈Rm×n，则具有共同类别属性的测试样本βi∈Rm就可以近似表示为第i类训练样本的线性组合，即

βi=xi1ai1+xi2ai2+…+xinain,

(14)

xi,j∈R;ai,j∈Rm；xi=[xi1,xi2,…,xin]。

式中：xi为样本βi在训练样本Ai下的稀疏表示系数;aij为第i类别下的第j个样本。

定义一个由y中4类训练样本集构成的完整样本字典A=[A1，A2，A3，A4]，则测试样本β在字典A下可表示为

β=Ax。

(15)

考虑数据噪声的情况下，稀疏表示问题可以表述为

(16)

对于测试样本β，可以通过优化目标(16)式求出其稀疏表示系数x，即得到测试样本在全局表示下的稀疏表示。实际应用中，由于噪声与模型错误，其非零元素通常会散布于较多类别间。为通过x完成分类工作，可采用分类函数

minri(y)=β-Aδi(x)2；i=1,2,3,4，

(17)

式中：函数δi表示保留第i类元素，其余元素置0。

3 实例分析

3.1 试验对象

选择美国凯斯西储大学电气工程实验室的轴承试验数据进行分析验证。轴承型号SKF6205,通过电火花加工单点损伤，损伤部位直径为0.036 mm，采样频率为48 kHz。试验模拟轴承在1 797 r/min时，钢球故障、内圈故障、外圈故障、正常工作共4种工作状态。

3.2 特征提取的对比分析

为了验证提出方法的提取效果，选择PCA、等距映射(ISOMAP)流形学习方法进行对比分析。均提取前3个主分量，使提取效果可视化。

3.2.1 PCA的特征提取

经PCA提取的前3个主分量为P1～P3，轴承的4种状态样本在三维子空间的分布如图1所示。

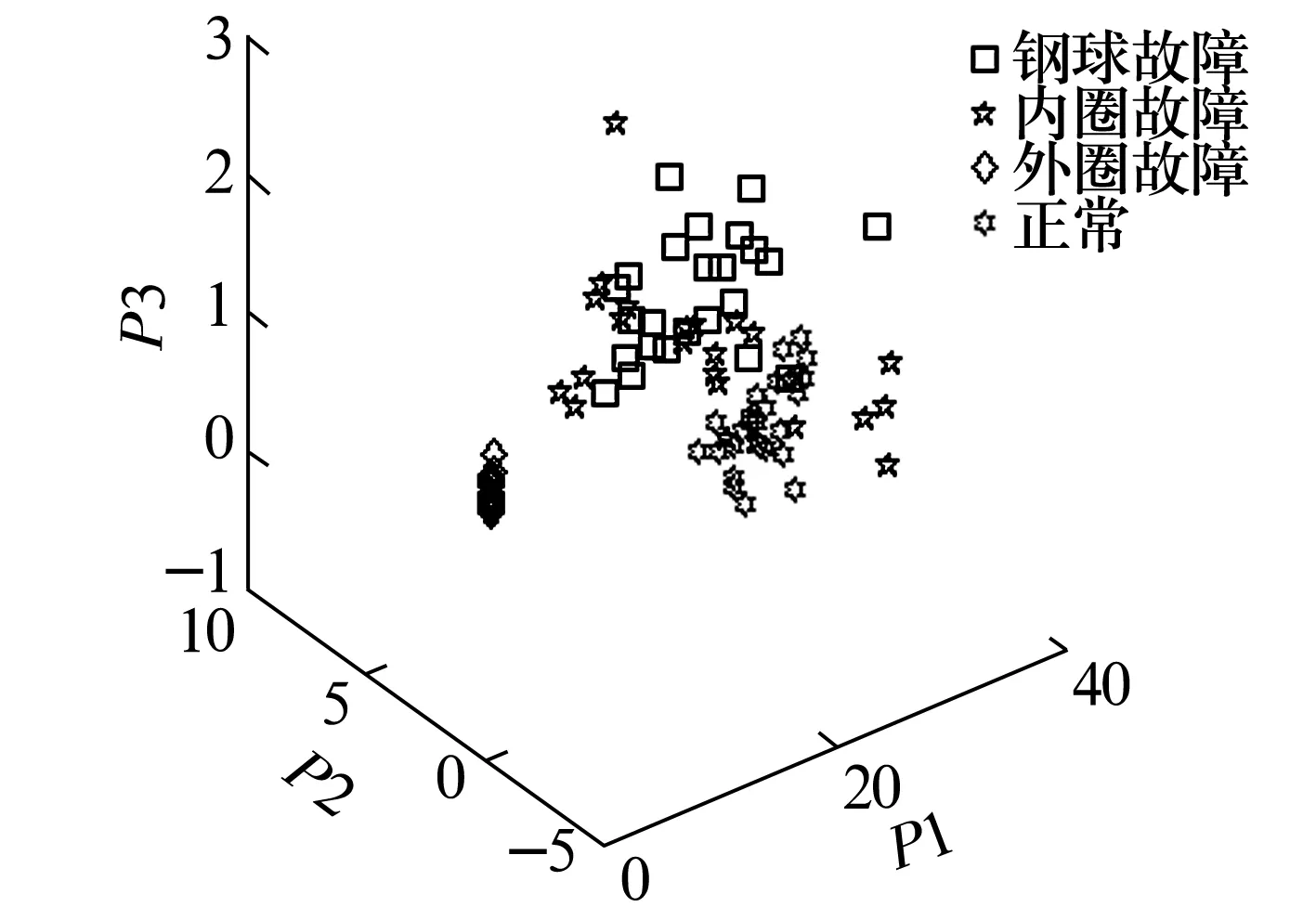
图1 PCA特征提取效果

由图可知，内圈故障样本与钢球故障样本重叠比较严重，并且分布较分散。有1个钢球故障样本与正常故障样本重叠，相对来说，正常样本与外圈故障样本聚类质量更良好。这是由于钢球故障表现为随机的冲击分量，包含冲击分量的样本与内圈故障样本接近。由此可见，PCA方法对轴承故障样本的聚类效果不太理想。

3.2.2 等距映射流形学习算法特征提取

等距映射流形学习算法的主要思想是利用局部邻域距离近似地计算数据点间的流形测地距离，并将高维数据间测地距离作为其本质低维表示间欧氏距离的不变特征量，进而完成数据降维。仿真试验中，通过ISOMAP提取的3个主分量为L1～L3，轴承的4种故障状态样本在三维子空间上的分布如图2所示，其中邻域K=5。

图2 ISOMAP特征提取效果

由图可知，正常状态样本和外圈故障状态样本有较好的聚类效果，而内圈故障状态样本分布较远、个别样本与滚动体故障状态样本发生重叠。由于ISOMAP属于非线性的流形学习算法，很好地揭示了高维数据的非线性结构，聚类性能相对于PCA得到了一定的提高，但ISOMAP的基本假设是全局等距映射和凸的数据空间，实际应用中难以满足。

3.2.3 低秩鉴别投影的特征提取

设置参数寻优范围:a为2～8，r为2-4～2-1，搜索步长为0.5。参数寻优结果如图3所示，图中水平面坐标分别取参数a，r的以2为底的对数，图中显示了低秩鉴别投影算法利用不同的参数对(a，r)所对应的轴承工作状态识别正确率。由图可知，当a=5.656 9，r=0.062 5时，状态识别率最高，因此，可以选择上述最优参数值作为LRDP的参数值提取轴承故障信息。

图3 参数寻优3D图

选择参数a=5.656 9，r=0.062 5，通过LRDP提取的3个主分量为K1～K3，轴承4种状态样本在三维子空间中的分布如图4所示，由图可知，LRDP完全准确地识别了轴承的不同故障状态，可以用于轴承故障诊断。

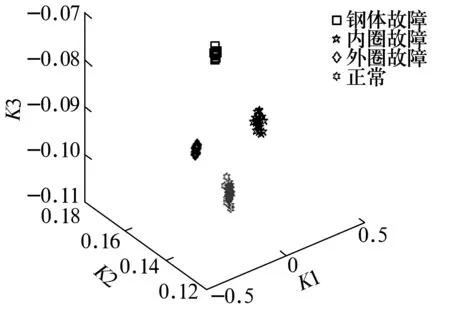
图4 LRDP特征提取效果

4 结束语

提出了一种基于低秩鉴别投影的故障特征提取方法，并与网格搜索法、稀疏表示分类器组合起来对算法中参数进行寻优。经仿真表明，低秩鉴别投影算法能够准确地描述数据的全局结构和判别结构，对于轴承故障特征提取是一种有效的特征提取算法。