基于蒙特卡罗法的城市燃气管网抗震连通可靠性分析*

赵慧乾，郭明珠，翟长达，石　松

(北京工业大学 建筑工程学院，北京 100124)



基于蒙特卡罗法的城市燃气管网抗震连通可靠性分析*

赵慧乾，郭明珠，翟长达，石松

(北京工业大学 建筑工程学院，北京 100124)

摘要：在对燃气管道进行地震反应判别的基础上，计算管道的抗震可靠度，并结合图论将城市燃气管网简化为源点、汇点和边线，建立管网简化模型。采用蒙特卡罗法对某六节点网络模型进行抗震连通可靠性分析，结果表明：随着迭代次数的增加，近似解以更小的误差接近精确解的概率更大；迭代次数取为5 000时，能够较好地满足精度要求。通过对连通性矩阵进行分析，探讨了设定源点提高目标汇点连通可靠度的可行性。最后，以保定市区的大型燃气管网为例，计算了Ⅶ～Ⅸ度地震烈度下管网的连通可靠度，对比了设定源点对汇点连通可靠度的影响，为该市燃气管网的震害预测和抗震优化提供参考。

关键词：蒙特卡罗法；城市燃气管网；设定源点；汇点；抗震连通可靠性度

0引言

城市燃气管网是城市生命线工程的重要组成部分，也是地震次生灾害源之一(Michael，Ronald，1996；周伟国等，2009)。燃气管网的抗震研究主要包括管道单体震害机理研究和网络可靠性分析两个方面(Li，He，2002)，其中，网络可靠性分析是研究热点。

目前，网络可靠性分析方法主要有解析算法和蒙特卡罗法(刘威，李杰，2002)。解析算法可以获得网络连通可靠度的精确解，但对于大型网络(节点超过100个)的求解，会因非多项式增长问题而导致计算困难。蒙特卡罗法是一种随机模拟方法，能够给出解的近似值(徐钟济，1985)，在网络连通性的计算分析中不考虑拓扑结构的复杂性，因而计算效率较高，随着迭代次数的增加，精度在一定范围内也会有不断提高的趋势，但难以预测精度是否满足要求。

1燃气管道抗震可靠度计算

1.1管道地震反应判别

城市燃气管网主要由埋地管道构成，其震害程度与地震动强度、场地土特质、管道特征等诸多因素有关(汤爱平，欧进萍，2002)。埋地管道在地震波作用下的可靠性分析主要有两种判别指标：对于接口式管道，以接口轴向形变作为判别指标；对于连续焊接管道，以应力作为判别指标。管道地震反应计算方法见郭恩栋等(1996)文献。

1.2管道抗震可靠度预测模型

在地震作用下管道的状态功能函数设为

Z=f(R,S)=R-S.

(1)

式中，R为管道判别指标的容许值，S为管道在地震作用下判别指标的计算值。

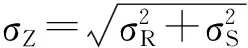
(2)

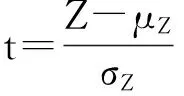
(3)

2燃气管网抗震连通可靠性分析

2.1基于图论的管网简化模型

图包括点和连接各点的矢量线，它是顶点集合和顶点的有序偶集合(E·米涅卡，1984)，图论正是研究图形而发展起来的理论。燃气管网通过管线和节点的相互连接构建成网络，将燃气储配站作为源点，管线交汇点、用户接入点作为汇点，管线作为连接各点的边，便可简化为图。通过分析计算不同地震烈度影响下的管段损坏的概率，对边赋予相应的权值，可以对源点与汇点的连通可靠度进行分析，进而得出网络的连通可靠度。

可用邻接矩阵A的形式表示图，便于进行数值分析。

A=[aij].

(4)

矩阵A中的元素用0和1进行表示，aij=1表示节点通过一条边可以实现连通，其中aij=1(i=j)表示节点i(j)存在自环线，这条线在管网简化图中并不存在，但仍取值为1。图1为一个含边权值的六节点网络图，1号节点为源点，其余各点为汇点，边线上的数字为权值。

若不考虑边权值，图1的邻接矩阵可用A表示。

(5)

图中各点能否通过若干边相互连接，可以用矩阵M表示：

M=A+A2+A3+……+An-1=[mij].

(6)

式中，n为节点数目mij≠0表示节点i，j通过若干条管线可以实现连通，否则为不连通。

2.2基于蒙特卡罗法的网络连通性分析

(1)用线性同余法产生0到1之间最大周期的伪随机数rij(吴新瞻，吴新垣，1990)，与计算所得的管线抗震可靠度pij比较，得到所有节点的邻接矩阵A，矩阵中元素aij的取值规则为

(7)

(2)计算M=A+A2+A3+……+An-1，n为节点数目。若mij≥1，则说明节点i和j之间连通；否则不连通。应该指出，除主对角线上的元素外，当M中所有元素均不为零时，所有节点均连通，即可停止计算，转入下一步骤。

(3)将步骤(2)中每次迭代的计算结果变换后，计入矩阵T中，T=[tij]。

(8)

(4)重复步骤(1)～(3)kmax次，即迭代次数，便可将节点连通频率作为源点与汇点之间连通可靠度的近似值。节点连通频率矩阵记为P，即连通性矩阵，可表示为

P=T/kmax.

(9)

与一般的数值模拟方法不同，蒙特卡罗法的收敛是概率意义下的收敛，不能断言其误差不超过某个值。将图1中边线上的权值视为相应边线的可靠度，并利用蒙特卡罗法计算各汇点的连通可靠度。图2为针对图1中2号汇点的迭代次数与相应误差关系的散点图，迭代次数最大为7 000次，步长为10，共计700个数据。从图2可以看出，选代次数10～3 000次，误差减小趋势明显；3 000～5 000次，误差基本能控制在2%以内；5 000～7 000次，误差的减少不甚明显，但随迭代次数增加，误差减小的趋势更为平稳，以更小的误差接近精确解的概率更大。

采用迭代5 000次的蒙特卡罗法对图1中每个汇点各重复计算6 000次，获得6 000组连通可靠度数据，用显著水平为0.000 063的置信区间表示近似解，并与全概率分解法(梅启智等，1992)计算的精确解对比，可以看出蒙特卡罗方法在大量数据支撑下，能够无限逼近精确解(表1)。由于实际应用中一般只计算一组连通可靠度数据，即单次模拟，再用这6 000组数据的均值与标准差来表示单次模拟所求近似解的精度。

从表1和图2可以看出，利用蒙特卡罗法迭代5 000次，能够将近似解的精度控制在一定的范围，根据管线的抗震可靠度计算精度的实际需求，可以直接应用单次模拟所求近似解。

网络连通性分析中，在不改变拓扑结构的情况下，汇点的连通可靠度与源点的相对位置有一定的关系，这在连通性矩阵Pij中有所表现，第i行中的每一个元素代表汇点(j≠1)与设定源点的连通性。图1的连通性矩阵中，元素与设定源点、汇点的对应关系见表2。通过连通性矩阵Pij可以看出，选取不同的节点作为源点，对诸多节点的连通可靠度有一定程度影响。

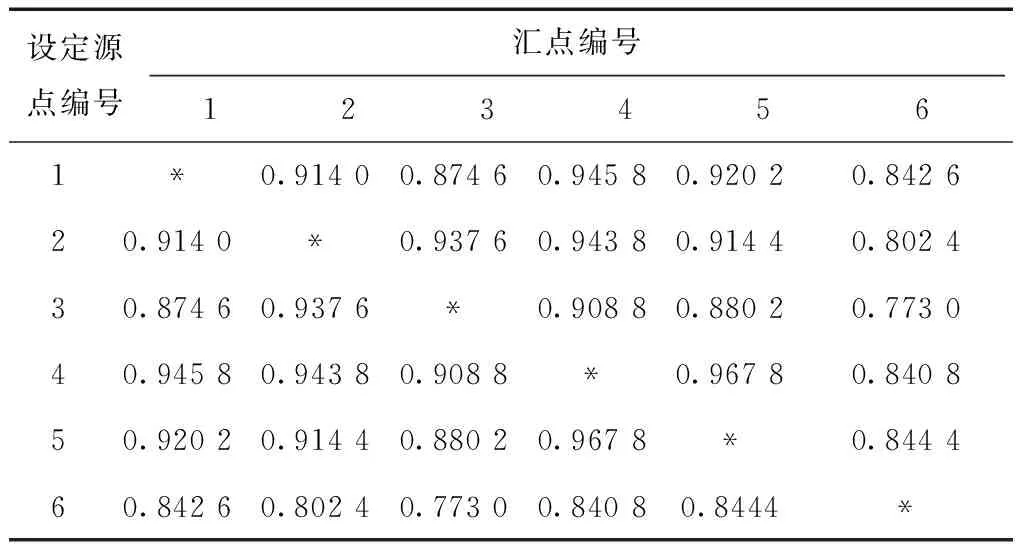
表2　连通性矩阵中源汇点对应关系

注：*为节点与自身的连通可靠度，不作讨论.

3工程实例

3.1工程概况

保定市城区燃气管网总长约229km，设计压力分级为中压A(0.4MPa)、中压B(0.03～0.07MPa)和低压(1.1～2.2kPa)。由于中压A管网以燃气储配站为供气源，独立成系统，可单独进行分析。中压A管网于2002年初投入使用，主要采用无缝钢管和Q235B直焊缝钢管，公称直径为250～500mm。市区场地土以Ⅲ类场地为主，部分地区为Ⅱ类场地。

3.2管网抗震连通性分析

现以燃气储配站为源点，将中压A管网简化为113个节点、141条边线的大型网络图(图3)。以应力为判别指标，计算各管线在Ⅶ度、Ⅷ度和Ⅸ度地震烈度下的抗震可靠度，并赋权给相应的边线，再用蒙特卡罗法迭代5 000次，求得不同汇点与源点的连通可靠度。

在不同地震烈度下，选取不同节点作为设定源点会对汇点抗震连通可靠度造成不同程度的影响。表3为在Ⅶ度、Ⅷ度和Ⅸ度地震烈度情况下，选取39号节点为设定源点时，与1号节点(燃气储配站)为源点时相比，部分汇点抗震连通可靠度变化幅度。从表中可以看出，在不同地震烈度下，设定源点对某些汇点连通可靠度的影响存在一定差别。

通过分析连通性矩阵可知，设定源点以改善局部重要节点或大部分节点的抗震连通可靠度是可行的(表4)。设定较优的源点，需要通过分析连通性矩阵，综合评定。如选取39号节点为设定源点，与1号节点为源点时相比，所有汇点抗震连通可靠度平均提高幅度为：Ⅶ度情况下，排名第1位，为10.22%；Ⅷ度情况下，排名第8位，为36.46%，但与排名首位的节点仅相差1.26%；Ⅸ度时，排名仅第25位，为203.55%，但此时汇点的连通可靠度已经普遍较低，排名高位也难以在实质上提高汇点的供气能力。此外，Ⅶ度、Ⅷ度和Ⅸ度情况下，连通可靠度≥0.800 0的汇点数目分别为81、30和0，与排名首位的节点相比，相差分别仅为1、6和4。因此，39号节点为较优的设定源点。

较优的设定源点多分布在管线密集的市中心，因此要考虑实际情况，在市区边缘选择合适的节点作为源点，而同时也需要着重对源点周边的网络拓扑结构进行优化。

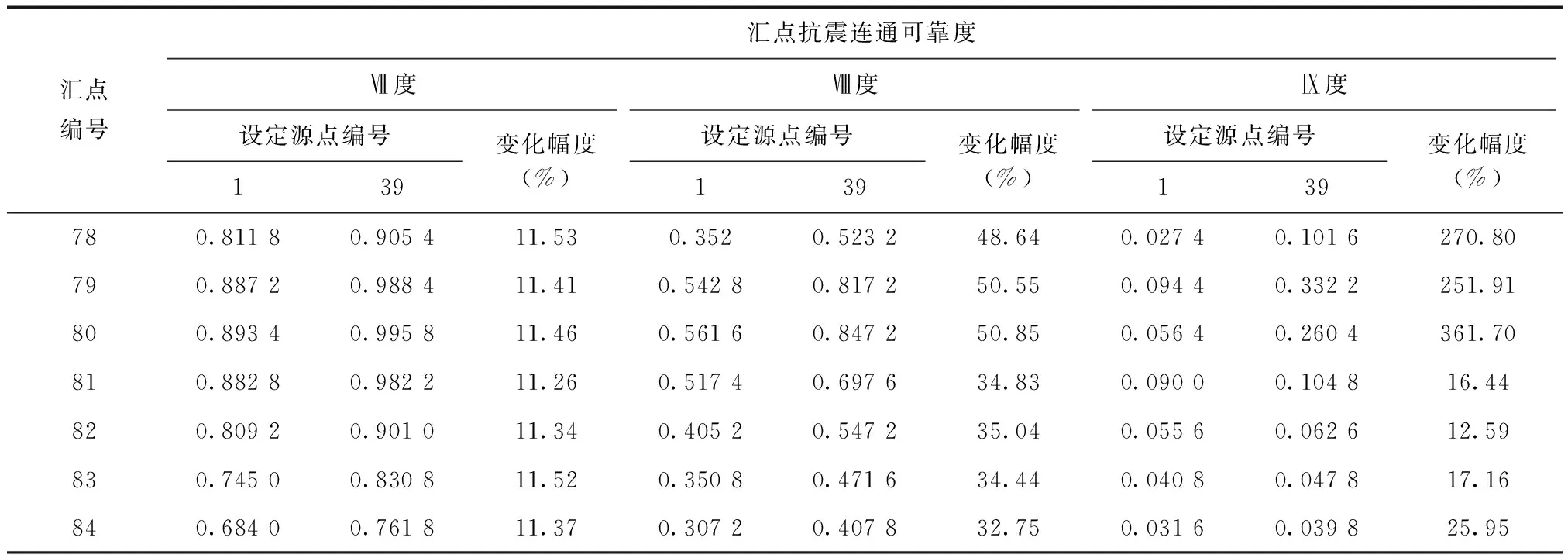
表3　不同地震烈度下设定源点对汇点连通可靠度的影响程度

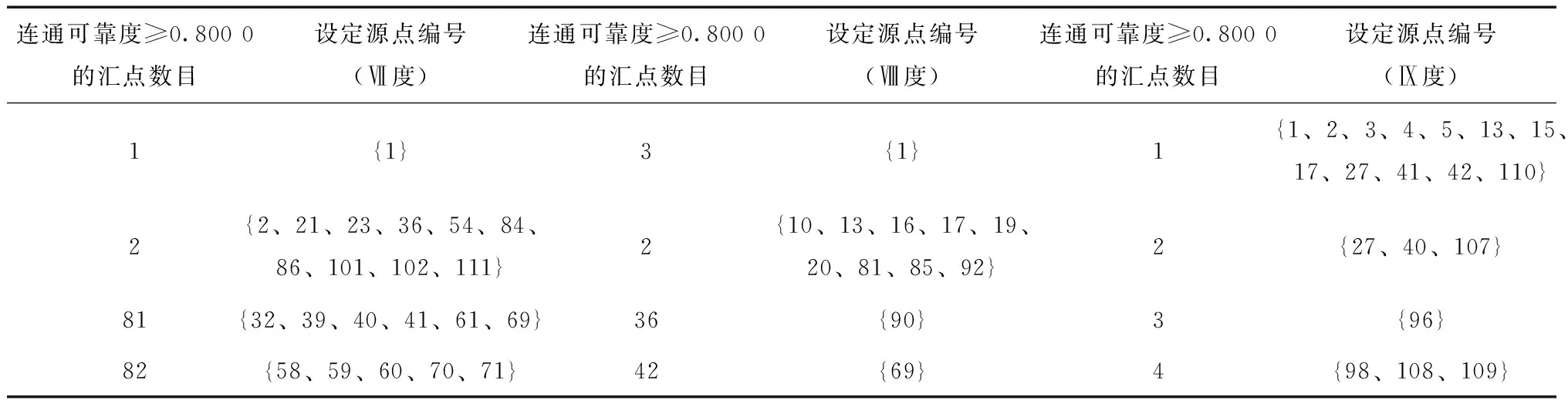
表4　不同地震烈度下设定源点的优劣对比

注：表中最后一行数据分别为Ⅶ～Ⅸ度地震烈度下，连通可靠度≥0.800 0的汇点数目最大值及其设定源点编号集合.

4结语

在城市燃气管网抗震连通可靠性分析中利用蒙特卡罗法，迭代5 000次即能满足相应的精度要求。

每个汇点与源点的连通可靠性与管道单体的抗震可靠性有关，但单纯依靠增大管径或采用抗震新型管材，经济成本较大。管网各汇点的抗震可靠性与源点的相对位置密切相关，需要综合实际情况来选取地理位置合适的源点。此外，增设新的源点或改善管网的拓扑结构来提高整个系统抗震可靠性也是很有成效的途径，但如何在一定的时间跨度内经济合理地实现这一目的，有待进一步研究。

本文资料的收集工作得到了保定市委、市政府，保定市科技局(地震局)，保定市燃气总公司等有关部门和单位的支持和帮助，在此一并表示感谢。

参考文献：

郭恩栋，冯启民，王亚东.1996.城市供水系统抗震可靠性分析及对策研究[J].地震工程与工程振动，16(3)：104-113.

刘威，李杰.2002.生命线网络可靠度分析的改进最小路递推分解算法[J].地震工程与工程震动，29(5)：66-72.

梅启智，廖炯生，孙惠中.1992.系统可靠性工程基础[M].北京：科学出版社.

汤爱平，欧进萍.2002.城镇埋地管网震害特征与破坏机理[J].地震工程与工程震动，22(4)：120-126.

吴新瞻，吴新垣.1990.随机模型与计算机模拟[M].北京：电子工业出版社.

徐钟济.1985.蒙特卡罗方法[M].上海：上海科学技术出版社.

周伟国，张中秀，孔令令.2009.城市燃气管网的震害分析及减灾对策[J].土木建筑与环境工程，31(4)：70-75.

E·米涅卡.1984.网络和图的最优化算法[M].北京：中国铁道出版社.

LiJ.，HeJ..2002.ARecursiveDecompositionAlgorithmforNetworkSeismicReliabilityEvaluation[J].EarthquakeEngineering&StructuralDynamics，31(8)：1525-1539.

MichaelK.L.，RonaldW.P..1996.IdentifyingandManagingConjointThreats：Earthquake-inducedHazardousMaterialsReleasesintheUS[J].JournalofHazardousMaterials，50(1)：31-46.

Basedondiscriminatingtheseismicresponseofgaspipeline，wecalculatedtheanti-seismicreliabilityofthepipe，andcombinedwithgraphtheory，wesimplifiedthecitygaspipelinenetworkasthesourcepoint，sinkpointandsidelinetoestablishthesimplifiedmodelofpipelinenetwork.Thenweanalyzedtheanti-seismicconnectivityreliabilityofacertainsix-nodenetworkmodelbyMonteCarlomethod.Theresultsshowedthatwiththeincreasingofiterationsnumber，theprobabilityoftheapproximatesolutionclosetotheexactsolutionwithasmallererrorisgreater.Settingthenumberofiterationsas5 000couldbettermeettheprecisionrequirement.Basedontheanalysisoftheconnectivitymatrix，wediscussedthefeasibilityofimprovingtheconnectivityreliabilityofthetargetsinkpointbyusingthesettingsourcepoint.Atlast，takingthelarge-scalegaspipelinenetworkindowntownBaodingasanexample，wecalculatedtheconnectivityreliabilityofpipelinenetworkunderearthquakeintensitiesfromⅦtoⅨdegree，andcomparedtheimpactofthesettingsourcepointontheconnectivityreliabilityofallthesinknodes，whichcouldprovidereferencesfortheseismicdamagepredictionandanti-seismicoptimizationofgaspipelinenetworkinthestudycity.

Keywords：MonteCarlomethod；citygaspipelinenetwork；setsourcenode；sinknode；anti-seismicconnectivityreliability

*收稿日期：2014-01-20. 基金项目：河北省城市活断层探测与地震危险性评价(保定市)项目[冀发改投资(2007)1689号]资助.

中图分类号：TV352

文献标识码：A

文章编号：1000-0666(2015)02-0292-05

AnalysisofAnti-seismicConnectivityReliabilityofCityGasPipeline
NeworkBasedonMonteCarloMethod

ZHAOHui-qian，GUOMing-zhu，ZHAIChang-da，SHISong

(CollegeofArchitectureandCivilEngineering，BeijingUniversityofTechnology，Beijing100124，China)

Abstract