薄板大挠度非线性弯曲问题的数值解

邵文婷(上海第二工业大学理学院,曙光研究院应用数学研究所,上海201209)

薄板大挠度非线性弯曲问题的数值解

邵文婷
(上海第二工业大学理学院,曙光研究院应用数学研究所,上海201209)

摘要:在前期工作中[1],对Chebyshev-Tau无网格高精度方法作了算法创新,从而改善了离散矩阵条件数病态问题。在此基础上,为了求解薄板大挠度非线性弯曲问题Von-K´arm´an系统,空间上采用Chebyshev-Tau无网格高精度方法,时间上采用无条件稳定的Newmark-β格式。针对simplified Von-K´arm´an系统及full Von-K´arm´an系统分别建立了迭代格式。通过一组具有精确解的数值算例验证了格式的有效性。相对传统的低阶数值方法,所提出的高精度方法在空间上达到谱精度,在时间上达到二阶精度。

关键词:Chebyshev-Tau无网格方法;薄板大挠度弯曲;非线性方程组数值计算

0　引言

薄板弯曲问题是弹性力学中重要的研究问题,其实质是求解高阶偏微分方程的问题。板壳理论根据描述问题的方程的性质分为线性板壳理论和非线性板壳理论。基于Kirchhoff假设条件,薄板弯曲小变形问题可以转化为弹性曲面线性微分方程: D∇4w=q,D是与板抗弯刚度及厚度有关。这是一个四阶线性的偏微分方程[1],针对板不同的边界条件,已经有了一套比较完整的理论分析和计算方法[2-4]。薄板的非线性弯曲,是指薄板弯曲程度较大,此时,Kirchhoff假定不再适当,必须考虑平行于板面的内力。第一个研究薄板非线性弯曲理论的学者Von-K´arm´an在20世纪初建立了薄板大挠度问题对应的非线性方程组,之后,许多工程师的工作集中在寻求有效而又简单的数值方法求解非线性方程组。在理论分析上,中国学者钱伟长教授提出了奇异摄动方法,是国际上最早用系统摄动法处理非线性方程的研究成果。自计算机发展至今,各种数值解法在计算力学和结构工程领域上解决了许多实际问题。然而目前在非线性板壳理论方面,用经典的有限差分法,难以得到收敛的迭代格式,所以这部分的数值计算仍然具有一定的挑战性。文献[5]运用变分原理推导并简化薄板弯曲大挠度高阶非线性偏微分方程,进一步将有限差分法和优化算法结合构建数值格式,计算精度达到3位有效数字。

高精度算法主要指微分求积法、谱方法、无网格方法等具有指数阶收敛的计算方法。无网格方法,是一种新兴的数值计算方法,根据展开级数构建方法和微分方程离散方法的不同,可以构建出不同的无网格方法。近10年,无网格方法在结构力学等工程领域上有很大的发展。Tau方法本质上是一种经典的谱方法。Chebyshev-Tau方法基于Chebyshev多项式展开,可以利用快速Fourier变换(FFT)提高计算效率。笔者之前的工作着重研究基于积分微分的Chebyshev-Tau方法求解薄板小挠度线性弯曲问题[5],通过数值算例说明基于积分微分的想法改善了离散矩阵的条件数。对于四阶问题,规则区域上的条件从O(N8)降低为O(N4),并且保留了传统的Chebyshev谱方法计算精度高的优点;同时积分过程引入的积分常数,使得该算法可以灵活处理边界条件。

本文考虑薄板大挠度非线性弯曲问题Von-K´arm´an系统的数值求解,其控制方程是由3个与时间变量有关的非线性偏微分方程组成的系统。空间上,相对低精度的有限差分法或者有限元法,采用高精度方法:基于积分微分的Chebyshev-Tau无网格方法(CTMMID)。时间方向上采用无条件稳定的Newmark-β格式。结合这两种方法来求解高阶非线性方程组是一种新的尝试。

1　薄板的大挠度非线性弯曲问题

考虑Von-K´arm´an非线性理论(1909)下的大挠度弯曲问题。假设正方形薄板Ω=[0,2]2,中面位移向量[u(x,y,t)v(x,y,t)w(x,y,t)]T,板中面的挠度函数w(x,y,t)。考虑如下无量纲形式的简化模型方程[6-7]:

式中:常数c与板的抗弯刚度D有关;υ为Poisson 比;h为板的厚度;在实际问题中通常gb(x,y,t)=0, gc(x,y,t)=0。板的四边满足固定边界条件: u=v=w=∂nw=0。

非线性方程式(1)∼(3)通常被称为full Von-K´arm´an系统,该系统存在唯一解,并且解有界[8]。特别地,注意到式(2)和(3)中前两项时间导数项,相对于方程中的其余项为h2量级,因此在一些文献中, 当h比较小时,舍去这些项,仅保留式(1)中带有时间的项。此时的方程组称为“simplified Von-K´arm´an”系统。

2空间离散格式CTMMID

Chebyshev谱方法应用于高阶方程时,离散矩阵的条件数通常比较大,求解四阶方程时,条件数为O(N8)。条件数的迅速增长会导致舍入误差影响计算精度[9]。前人在改善Chebyshev谱方法的条件数上做了大量工作,然而这些改进对高阶、高维问题都有局限性[10-13]。本节中,介绍基于积分微分的Chebyshev-Tau无网格方法。前期工作[5]通过大量的数值算例说明基于积分微分过程可以将矩形区域上四阶方程的条件数改善为O(N4)。

2.1一维问题

2.1.1预备知识

Chebyshev多项式{Ti(x)},x∈[−1,1]满足积分公式:

假设函数u(x),ux(x),uxx(x)有如下Chebyshev多项式展开:

令

根据式(4)、(5),得到关系式:

式中,H0,H1,H2为(N−2)×N阶积分矩阵。

另一方面,关于微分过程有如下引理。

引理1[14-15]设光滑函数u(x)有Chebyshev多

式中,D(1)和D(2)均为上三角矩阵,

实际计算时,考虑截断的Chebyshev多项式展开u(x)≃。简单起见,仍记截断后的微分矩阵为D(1)和D(2),即D(j)=

进一步,记向量d和e分别为uxxx和uxxxx的Chebyshev系数。由式(9)和系数向量U的定义,有:

式中:D1=[0(N−2)×2D(1)],D2=[0(N−2)×2D(2)], E≡H0。

最后,由矩阵和向量的运算得到:

2.1.2方程离散

考虑如下模型问题

式中,α,β,p1,p2,s1,s2为常数。

假设 f(x)≃ [T0(x) ···TN−3(x)]F,F= [f0···fN−3]T,利用上节介绍的数值方法,式(13)离散为

积分过程引入的系数可以由边界条件确定。

边界条件离散如下:

解得

式中,Qi,ti(i=1,···,4)均为已知量。

2.2二维问题

2.2.1Chebyshev积分微分过程

CTMMID离散方程的出发点是对方程中出现的交叉导数项uxxyy(x,y)进行逼近。假设

记系数矩阵:

则uxx=[aci,j],uyy=[cai,j]满足

类似地,设uxxxx(x,y)和uyyyy(x,y)的Chebyshev多项式逼近

其系数矩阵ec=[eci,j]和ce=[cei,j]满足

考虑如下方程

由离散格式的矩阵表达式(19)及(20),得到

式中,矩阵LHS=[H2⊗D2+2E⊗E+D2⊗H2−(H2⊗E+E⊗H2)+H2⊗H2]。

2.2.2固定边界条件离散

对矩形板,挠度函数u(x,y)满足固定边界条件

由矩阵分块的技巧随后,建立U22和其余3块U11,U12,U21之间的关系式。

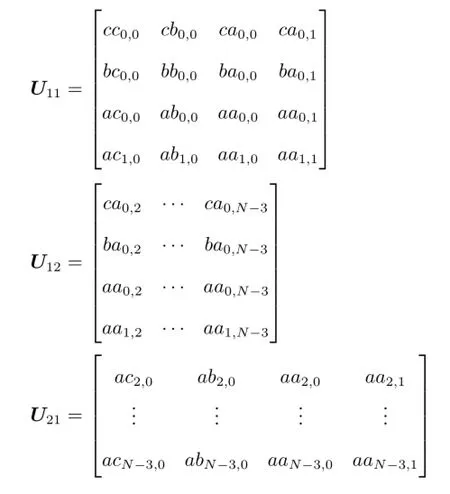
令 uyy(−1,y)=(y),uyy(1,y)=(y), uxyy(−1,y)=(y),uxyy(1,y)=(y),类似式(16),得到:

另一个变量方向上,令

此外,有

最后,令

类似式(24)定义函数tbj(x),tcj(x),j=1,2,3,4。结合式(27)得到,

其中:

将式(25)代入上式:

式中:W11=11W12;g11=11g12+11。

类似一维情况,由式(25)∼(28),问题最终转化为求解系数矩阵Vec(U22)满足的线代方程组。

3　时间离散格式Newmark-β

对于模型方程:

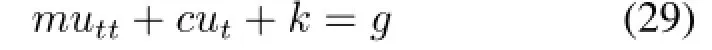
式中,右端项g可以是关于u的函数。

利用Newmark-β时间离散格式[17],参数选取γ=1/2,β=1/4。第(n+1)时间层上un+1与第n时间层上un满足的离散方程

该格式的局部截断误差为O((∆t)2),并且无条件稳定。

4　数值算例

4.1线性弯曲问题

考虑模型问题[6]

及其边界条件:

初始条件:

受迫项:

取精确解:

首先利用格式(30)对式(31)进行时间方向离散:

进一步采用CTMMID进行空间方向上的离散。

图1　t=1,线性弯曲问题(31)的数值结果Fig.1 t=1,The numerical results of the linear bending problem(31)

数值结果如下:图1(a)呈现了空间方向上的收敛性,达到了谱精度;图1(b)给出了对应不同时间步长的L∞误差,时间方向上达到二阶精度。

4.2大挠度非线性弯曲问题

考虑full Von-Ka´rma´n系统式(1),c=0,υ=0.3, h=。取精确解[6]:

时间方向离散后,进行线性化,建立迭代格式:

对于simplified Von-K´arm´an系统,同样考虑精确解(33)。建立迭代格式

利用迭代格式(34)∼(36)或(37)和(38)计算第(n+1)时间层上数值解:利用已求得上一时间层的数值解wn,un,vn作为初始值wn+1,0,un+1,0,vn+1,0进行迭代。当两相邻迭代层上的数值解满足|wn+1,k+1−wn+1,k|

表1　求解simplified Von-K´arm´an系统的L∞误差(t=2)Tab.1 The L∞errors for solving the simplified Von-K´arm´an system(t=2)

表1列出了求解simplified Von-K´arm´an系统,分别选取∆t=10−2,10−3,计算t=2的数值解,L∞误差随项数N−2的变化。可以看出在空间上为谱精度,时间上达到了二阶精度。但是当计算的时间更长时,simplified Von-K´arm´an系统会出现不稳定的现象,而full von-K´arm´an系统可以计算的时间更长, 表2列出了求解full von-K´arm´an系统,t=4的数值结果。

表2　求解full von-K´arm´an系统的L∞误差(t=4)Tab.2 The L∞errors for solving the full von-K´arm´an system(t=4)

5　结语

本文采用基于积分微分的Chebyshev-Tau无网格高精度方法求解薄板大挠度非线性弯曲问题。时间方向上采用无条件稳定的Newmark-β格式。通过一组具有精确解的模型问题进行数值验证,结果表明这两种离散方法的结合是有效的。相对传统的低阶数值方法,本文提出的数值方法在空间上达到谱精度,在时间上达到二阶精度。

对本文中所考虑的这类非线性方程组的数值求解,面临长时间计算不稳定的问题。为了克服这个困难,目前的研究工作正在进一步尝试对CTMMID离散格式设计一种合适的滤波器函数。

参考文献:

[1]严宗达.结构力学中的富里叶级数解法[M].天津:天津大学出版社,1989.

[2]曲庆璋,章权,季求知,等.弹性薄板理论[M].北京:人民交通出版社,2000.

[3]SHAO W T,WU X H.Fourier dfferential quadrature method for irregular thin plate bending problems on Winkler foundation[J].Eng Anal Bound Elem,2011,35(3): 389-394.

[4]SHAO W T,WU X H,CHEN S Q.Chebyshev tau meshless method based on the integration-differentiation for Biharmonic-type equations on irregular domain[J].Eng Anal Bound Elem,2012,36(12):1787-1798.

[5]候祥林,郑夕健,张良,等.薄板弯曲大变形高阶非线性偏微分方程推导与优化算法研究[J].物理学报,2012, 61(18):180-201.

[6]KIRBY R M,YOSIBASH Z.Solution of von-K´arm´an dynamic non-linear plate equations using a pseudo-spectral method[J].Comput Methods Appl Mech Eng,2004, 193(6-8):575-599.

[7]NATH Y,KUMAR S.Chebyshev series solution to nonlinear boundary value problems inrectangular domain[J]. Comput Methods Appl Mech Eng,1995,125(1-4):41-52.

[8]YOSIBASH Z,KIRBY R M,GOTTLIEB D.Collocation methods for the solution of von-K´arm´an dynamic nonlinear plate systems[J].J Comput Phys,2004,200(2):432-461.

[9]MUITE B K.A numerical comparison of Chebyshev methods for solving fourth order semilinear initial boundary value problems[J].J Comput Appl Math,2010,234(2): 317-342.

[10]HEINRICHS W.Improved condition number for spectral methods[J].Math Comput,1989,53:103-119.

[11]HEINRICHS W.A stabilized treatment of the biharmonic operator with spectral methods[J].Siam J Sci Comput, 1991,12:1162-1172.

[12]HEINRICHS W.Stabilization techniques for spectralmethods[J].J Sci Comput,1991,6:1-19.

[13]SQUIRE W,TRAPP G.Using complex variables to estimate derivatives of real functions[J].Siam Rev,1998, 40(1):110-112.

[14]CANUTO C,HUSSAINI M Y,QUARTERONI A,et al. Spectral methods:Fundamentals in single domains[M]. Berlin:Springer-Verlag,2006.

[15]BOYD J P.Chebyshev and fourier spectral methods[M]. New York:DOVER Publications,2001.

[16]KONG W,WU X.Chebyshev tau matrix method for Poisson-type equations in irregular domain[J].J Comput Appl Math,2009,228(1):158-167.

[17]HUMAR J L.Dynamics of Structures[M].Balkema:CRC Press,2002.

中图分类号:O241.82

文献标志码:A

文章编号:1001-4543(2015)03-0209-09

收稿日期:2015-04-26

通讯作者:邵文婷(1987–),女,上海人,讲师,博士,主要研究方向为偏微分方程数值解。电子邮箱wtshao@sspu.edu.cn。

基金项目:上海第二工业大学校基金(No.EGD15XQD13)、上海高校青年教师资助计划项目(No.ZZEGD15008)、上海第二工业大学重点学科建设项目(No.XXKZD1304)、上海第二工业大学曙光研究院应用数学研究所(No.A01GY15GT01)资助

The Numerical Solution of the Nonlinear Big Bending
Problem of the Thin Plate

SHAO Wen-ting
(School of Science,Institute of Applied Mathematics of“Dawn”Academy,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

Abstract:In previous work[1],research on Chebyshev-Tau meshless method with high order accuracy have been done.It improves the condition number of the coefficients matrix.It is major in the numerical solution of the nonlinear bending problem of the thin plate.A method is presented,which combines the Chebyshev-Tau meshless high order method in space with the unconditionally stable Newmark-β scheme in time,and utilize it to solve the Von-K´arm´an system.Besides,the iteration schemes for the simplified and the full Von-K´arm´an system is established,respectively.Numerical examples with exact solutions show that this proposed numerical method works well,it reaches spectral accuracy in space and second order accuracy in time.

Keywords:Chebyshev-Tau meshless method;the big vibration problem of the thin plate;numerical solution of the system of nonlinear equations