加速度滞后补偿与模糊自适应PI相结合的伺服控制算法
吴滢跃,汤心溢,于 洋,刘士建(中科院上海技术物理研究所,上海200083)
加速度滞后补偿与模糊自适应PI相结合的伺服控制算法
吴滢跃,汤心溢,于洋,刘士建
(中科院上海技术物理研究所,上海200083)
摘要:提出了一种加速度滞后补偿与模糊自适应PI相结合的伺服控制算法。这种算法利用模糊规则制定相应的PI控制参数,针对大机动运动目标的特性,采用加速度滞后补偿方法,两种算法的有效结合提高了伺服系统的跟踪精度以及动态响应能力。该算法运算量小,实时性好,可在硬件上实现。实验表明,此算法对最高速度为30◦/s、最高加速度为10◦/s2的运动目标可以实现快速地捕获以及稳定地跟踪,跟踪精度均方值为13.8′′。
关键词:加速度滞后补偿;模糊算法;伺服控制
0 引言
对于低速运动目标,无论是加速度滞后补偿方法还是模糊自适应PI控制算法都能取得很高的跟踪精度[1]。加速度滞后补偿方法对高速机动目标的跟踪精度也可以达到较高的水平,但由于加加速度甚至更高阶加加加速度的存在以及系统对速度与加速度预测的误差[2],导致这种控制方法无法达到更高的跟踪精度要求;模糊自适应PI算法在稳定跟踪阶段有很好的表现,但是在跟踪初始阶段往往由于目标机动性太强而导致跟踪失败[3]。
任何信号都可看成直流信号与小交流信号的叠加[4-5],基于此,提出一种新的伺服控制方法,即加速度滞后补偿与模糊自适应PI控制结合的算法。其中加速度滞后补偿用来处理大分量“直流信号”,模糊自适应PI控制算法补偿小分量“交流信号”。
1 算法描述
如图1所示,光滑曲线表示目标真实运动轨迹,虚线表示根据编码器预测滤波得到的预测目标运动速度,光滑曲线与虚线之差即为需要的补偿输出值。这个差值为预测误差、响应延时误差与高阶机动项(加加速度,加加加速度等)之和,因此该差值为一较小值。前面提到,模糊自适应PI控制算法对低速运动目标可以达到很高的跟踪精度,图中所示的差值可以等效为低速运动目标。
图2为算法结构图,把脱靶量的值与差分值输入模糊控制器,得到自适应模糊控制PI参数∆kp和∆ki,把编码器的值通过一次求导与两次求导后,得到等效速度与等效加速度,再经过滤波、加权处理后作为前馈输入速度环前端。控制器输出函数为

其中:Kp0和Ki0为常规PI控制器得到的初始值; ∆kp和∆ki为模糊自适应控制器求得的比例系数与积分系数变化量;kv为速度补偿因子;ka为加速度补偿因子;∆t为脱靶量间隔时间。

图2 加速度滞后补偿与模糊自适应PI控制结合算法框图Fig.2 Block diagram of algorithm based on acceleration delay compensation and fuzzy-PI control
模糊控制器参数的确定:
定义E为e的模糊映射,∆E为∆e的模糊映射,它们的映射关系分别如下:

定义 E 和 ∆E 的论域为 {−3,3},定义∆kp的论域为 {−1.5,1.5},定义 ∆ki的论域为{−0.24,0.24}。
取E、∆E、∆kp和∆ki的模糊子集为{NB, NM,NS,Z,PS,PM,PB},其中N表示Negative,P表示Positive,B表示Big,M表示Medium,S表示Small,Z表示Zero。模糊子集中分别表示负大,负中,负小,零,正小,正中,正大。E、∆E、∆kp和∆ki的隶属函数曲线图分别如图3(a)∼3(d)所示。

图3 隶属度函数图Fig.3 Diagram of membership function
本文的模糊自适应PI控制器中的模糊规则采用Mamdani推理法[6],这种推理法本质上还是一种合成推理方法。模糊规则的制定[7]主要取决于控制经验。Mamdani的关系生成算法取min运算:

来自U和V的一对元素(x,y)其模糊关系R= (A→B)的程度为:

推理合成算法取max-min复合运算

即

将关系生成算法与推理合成算法合并到一起即得
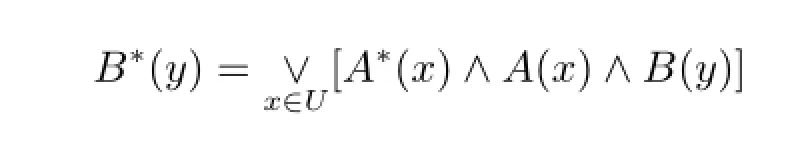
这就是简单模糊推理模型的Mamdani算法。
举例说明,如果e为NB,∆e也为NB,表明此时系统正处于负超调的背离运动,且背离值为大,因此需要把Kp加到最大,把Ki减到最小以减少积分项的惯性,使系统尽快回头作趋近运动,所以Kp模糊取值为PB,Ki模糊取值为NB。Kp执行规则见表1, Ki执行规则见表2。

表1 ∆kp模糊规则表Tab.1 Fuzzy rules of∆kp

表2 ∆ki模糊规则表Tab.2 Fuzzy rules of∆ki
为求得最终的∆kp和∆ki,需对模糊量进行清晰化。模糊量的清晰化有如下几种方法:重心法、加权平均法、左取大和右取大法以及最大隶属度法。本文采用重心法对PI模糊控制器进行清晰化。
重心法是把重心对应的基础变量值作为清晰值,重心取自模糊集隶属度函数曲线与基础变量所围面积,其计算公式表示为

式中u∗为清晰化输出量,µ为模糊集隶属函数,umin为清晰化值的下限,umax为清晰化值的上限。
2 实验结果及分析
为了验证算法的有效性,选择一种接近真实运动轨迹的曲线来模拟目标[8]。由傅里叶变换原理可知,任何运动轨迹都可以看成是由若干个正弦曲线合成的。由于正弦曲线的一阶导数为余弦,二阶导数是正弦,意味着模拟目标的速度和加速度都是时时刻刻在变化的。因此选择最大速度为30◦/s,最大加速度为10◦/s2的正弦曲线θ(t)=90sin(0.33t)作为输入测试曲线,输入某在研跟踪设备。
原有的控制算法一般采用速度滞后补偿或加速度滞后补偿,在实际应用中,这两种算法对机动性较强的运动目标的跟踪效果不佳。实验中分别采用速度滞后补偿、加速度滞后补偿、加速度滞后补偿与模糊自适应PI控制相结合的算法对系统进行半实物仿真。仿真结果如图4∼6所示。
半实物仿真测试结果表明(见表3):速度滞后补偿在小加速度情况下跟踪效果良好,在加速度变大时,稳态跟踪误差变大;在速度滞后补偿的基础上增加了加速度滞后补偿,动态响应时间和稳态跟踪误差都有所减小;采用本文的加速度滞后补偿与模糊自适应PI控制相结合的算法后,动态响应能力和跟踪精度有了进一步提高。

图4 速度滞后补偿算法跟踪误差曲线Fig.4 Tracking error curve of velocity lag compensation

图5 加速度滞后补偿算法跟踪误差曲线Fig.5 Tracking error curve of acceleration lag compensation

图6 加速度滞后补偿与模糊自适应PI算法跟踪误差曲线Fig.6 Tracking error curve of acceleration lag compensation combined with fuzzy-PI

表3 3种算法的跟踪结果Tab.3 Comparison of three algorithms
3 结语
针对大机动运动目标的跟踪,本文提出一种加速度滞后补偿与模糊自适应PI相结合的伺服控制算法。把目标运动轨迹划分为低频部分和高频部分,加速度滞后补偿处理低频部分,模糊自适应PI控制处理高频部分。由半实物仿真实验可知,此算法有效提高了伺服系统动态响应能力和稳态跟踪精度。
参考文献:
[1]王建立.光电经纬仪图像跟踪、捕获快速运动目标技术的研究[D].长春:中国科学院研究生院,2002.
[2]杜杰.基于加速度计的光电伺服跟踪系统前馈控制[D].长春:中国科学院长春光学精密机械与物理研究所, 2011.
[3]ISHIDA T,MIYATA K,KOMURA N,et al.Demodulation of servo tracking signals printed with a lithographically patterned master disk[J].IEEE Transactions on Magnetics,2001,37(4):1412-1415.
[4]SOLIMAN H F,ATTIA A A,BADR M A L,et al.Fuzzy logic controller for electric motor driving the astronomical telescope[J].SPIE,1998,3351:415-424.
[5]秦继荣,沈安俊.现代直流伺服控制技术及其系统设计[M].北京:机械工业出版社,1999.
[6]韩晓泉.模糊控制在光电跟踪伺服系统中的应用研究[D].长春:中国科学院研究生院,2004.
[7]王永福,王殿辉,柴天佑.一个具有完备性和鲁棒性的模糊规则提取算法[J].自动化学报,2010,36(9):1337-1342.
[8]胡寿松.自动控制原理[M].3版.北京:国防工业出版社,1994.
中图分类号:TN98
文献标志码:A
文章编号:1001-4543(2015)03-0205-04
收稿日期:2015-06-03
通讯作者:汤心溢(1970–),男,江苏溧阳人,研究员,博士,主要研究方向为光电对抗技术。电子邮箱gq227@mail.sitp.ac.cn。
基金项目:国家“十二五”国防预研项目(No.41101050501)资助
A Servo Control Algorithm Based on Acceleration Delay Compensation and Fuzzy-PI Control
WU Ying-yue,TANG Xin-yi,YU Yang,LIU Shi-jian
(Shanghai Institute of Technical Physics of CAS,Shanghai 200083,P.R.China)
Abstract:A servo control algorithm based on acceleration delay compensation and fuzzy-PI control is described.This algorithm uses fuzzy rules to formulate the corresponding PI control parameters.For the characteristics of large maneuvering target,the acceleration delay compensation method is adopted.The effective combination of two algorithms improves the tracking accuracy and the dynamic response capability of the servo system.This algorithm has small computation,good real-time,and can be realized in hardware. Experiments show that the algorithm can achieve fast tracking and stable tracking for fast moving target(The maximum acceleration of the target is 30◦/s and the maximum acceleration is 10◦/s2.),tracking accuracy of 13.8′′.
Keywords:acceleration lag compensation;fuzzy algorithm;servo control

