基于前馈补偿加速度权系数的独立变桨距控制研究
范定成,秦斌,姜学想(湖南工业大学 电气与信息工程学院,株洲 412007)
基于前馈补偿加速度权系数的独立变桨距控制研究
范定成,秦斌,姜学想
(湖南工业大学 电气与信息工程学院,株洲 412007)
摘要:风能发电系统具有自然风速的随机性、时变性和系统的非线性等特点,所以论文提出了基于前馈补偿加速度权系数的独立变桨距控制方法。采用加速度权系数分配对各个桨叶单独进行控制,使每个桨叶跟随风速的变化而变化,实现独立变桨距控制,然后根据前馈补偿理论的知识对整个控制过程进行补偿。论文构建了直驱永磁同步发电系统独立变桨距的数学模型,并在MATLAB/Simulink上进行建模仿真,仿真结果表明论文提出的控制算法不仅具有强抗干扰、强鲁棒性以及响应速度快的优点,而且还可以在稳定系统输出功率的同时,实现各桨叶的平稳变化,减轻风力发电机组疲劳载荷和摩擦。
关键词:风力发电系统;变桨距控制;前馈补偿;加速度权系数
本文引用格式:范定成,秦斌,姜学想.基于前馈补偿加速度权系数的独立变桨距控制研究[J].新型工业化,2015,5(8):26-32
Citation: FAN Ding-cheng, QIN Bin, JIANG Xue-xiang. A Control Method For Invidual Pitch Based on Feedforward Compensator Accelerated Speed Weight Number Assignment[J]. The Journal of New Industrialization, 2015, 5(8): 26-32.
0 引言
由于风能是可再生能源,所以风能发电必成为可持续发展道路。变桨控制已经逐渐成为风力发电技术的主流技术,负责空气动力系统的桨距自动调节,实现高风速段发电机的稳定输出。目前,诞生了两种控制方法,分别是统一变桨距控制和独立变桨距控制。事实上,统一变桨距控制很难达到上述设计要求,因为三个桨叶由同一个执行机构统一控制,步调同一变化,而在独立变桨距控制中,三个桨叶分别由不同的执行机构控制,彼此之间独立,互不联系。当其中一个执行结构发生故障,导致其所控制的桨叶不能实现变桨时,另外两个桨叶却能在自己的执行机构控制下实现单独变桨,也就是说整个风力发电机组可以继续带伤工作,彼此之间相互独立,互不影响。当风力机转到不同位置时,尽管风速也随着时间不同而变化,但是独立变桨距控制技术可根据不同叶片受力不同,对每个桨叶进行独立控制,使桨距角跟随风速而增大或减小,从而减小桨叶的拍打振动,最终使发电机的输出功率稳定在额定功率附近,延长风力机的寿命。所以独立变桨距控制技术值得我们去研究。
论文研究的目地是使发电机的输出功率稳定在额定功率的条件下,使系统能更快的响应输入的变化,同时使输出的功率的变化频率和幅值更小。为了达到上述要求,提出了基于前馈补偿加速度权系数独立变桨距控制方法,最后通过对一台额定输出功率为2MW的永磁同步发电进行建模仿真,结果表明论文提出的控制方法是正确的,而且是有效的,因为不仅保证了发电机输出功率的稳定性,还从另一方面减小了桨叶的振荡和机组的载荷,故此方法是可行的。
1 风力发电系统建模
由于机械时间常数远远大于电磁时间常数,所以在论文的研究过程中,忽略了电磁时间常数,即不考虑发电机的电磁动态响应过程。图1是永磁同步发电机发电和并网运行的结构框图,其中发电机的转速通过机侧控制单元利用电磁转矩进行控制,在额定风速以下时,使发电机运行在最佳叶尖速比位置,充分吸收风能,当风速大于额定风速小于切出风速时,发电机的转速由变桨距执行机构单元控制桨叶桨距角进行间接控制,从而保持输出功率的恒定。就这样通过变桨距控制单元和机侧控制单元的共同作用,即使风速不断变化时,机组系统也能稳定工作。
1.1 风速特性分析
自然界的风是立体的,而且无论是在时间上还是空间上,它都是不断变化的,这种变化随着高度的更加变化更明显,因此当风能吹向风轮平面时,各桨叶受到的风速风力是不相同的。随着风能发电技术的发展,风力机变得越来越大型化,桨叶从最初的数米增加到如今的数十米,高度成为众多因素中影响风速的决定因素,而其它一些随机干扰可能随着高度的增加而互相相互抵消减弱。风切效应和塔影效应是影响风速在竖直高度方向上变化主要原因。
当风速稳定时,随着高度增加风速发生变化,这就是风切效应。设地面风速为零风速,则有风切经验公式为[2]:

图1 风力机驱动的PMSG框图Fig.1 The PMSG diagram of wind turbine drive

式中,VH为距水平地面高H处的风速;VH0为距水平地面高H0处的风速;n为风切系数,取决于地表的凹凸程度和空气稳定度。
当风能吹过塔架时,塔架对流过它的气流具有一定的阻碍作用,使沿风速方向上游和下游风速大小发生变化,这就是塔影效应。风力机在塔影坐标系下垂直于风轮旋转面的某点的风速可以用下式表示:
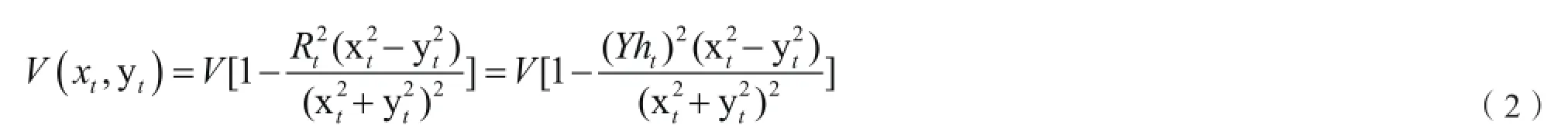
1.2 空气动力学分析
变桨距控制都是针对不断旋转的风轮叶片进行控制的,而且当风速在额定风速以上时,整个风轮的旋转速度基本是保持不变的,所以在这里只分析当风轮起动后以某恒定速度稳定运行时叶片的受力状况,桨叶受力如图2所示。
由叶素理论可得,当风轮旋转以角速度ω旋转时,在距离风轮中心r处取一长度为dr的叶素,设其桨距角为β,则作用在此叶素上的力dF可分解为沿风轮旋转切线方向的力dFa和沿风轮轴向的力dFt,则叶素上的切向力和轴向力分别为:


图2 叶片坐标系Fig.2 Blade coordinate system
式中,ρ为空气的密度;V为相对风速;dS为叶素元的桨叶面积;φ为来流角,是风轮平面与相对风速V间的夹角,等于叶素攻角与桨距角之和;CL和CD分别为桨叶阻力系数和桨叶升力系数,它们只与桨叶的形状有关。
1.3 永磁同步电机模型
在转子旋转坐标系下,永磁同步电机的数学模型经过坐标变换后,d轴、q轴之间的电流就不存在耦合关系了,进而可以对id和iq进行独立控制。根据坐标变换理论与旋转的dq轴坐标系知识,可得永磁同步电机的数学模型如下:

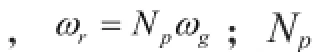
假设直驱永磁同步电机dq轴电感是相等的,则由电磁转矩表达式可得:

在风力发电系统中,永磁同步电发电机与风力机不经过增速箱而直接连接。与所有电动机相类似,永磁同步发电机的机械机构,即传动部分动态模型可以用一个一阶微分方程表示:
设计与研究

式中,Tw是气动转矩;Te是电磁转矩;B是发电机的摩擦系数;ωg是发电机转子转速;J是风轮发电机整体转动惯量。
2 基于前馈补偿加速度权系数独立变桨距控制
2.1 基于加速度权系数分配变桨距控制策略
目前风力发电独立变桨距技术主要有两种:①基于桨叶加速度独立变桨;②基于桨叶方位角独立变桨。利用加速度传感器最具明显优势的就是直接检测风机叶片的受力状况,而基于此所建立起来的独立变桨距控制策略分为两个部分,第一部分是功率控制器,采用模糊控制器对系统进行控制,可以得到系统的统一桨距角给定值。第二部分是加速度权系数独立变桨距控制器,由权系数分配单元、前馈补偿和权系数调整运算单元组成。权系数分配单元得到优化设计的权系数,权系数是依据桨叶受力情况进行分配的,受力越大,桨距角的变化量就越大,权系也就越大,反之受力越小,桨距角的变化量就越小,权系也就越小。整个控制思路是:当风速在额定风速以下时,由于风速比较小,桨叶桨距角都保持在3°左右,最大吸收风能;当风速高于额定风速时,首先要保证功率控制的要求,通过模糊算法得出三个桨叶统一的桨叶节距角,而后将桨叶加速度信号作为权系数重新调整各桨叶的桨距角。权系数分配独立变桨控制如框图3所示。

图3 基于前馈补偿加速度权系数分配变桨距控制Fig. 3 Based on the feedforward compensation acceleration weight coefficient assigned variable pitch control
2.2 权系数分配运算单元
先通过模糊算法得到三个桨叶共同的桨叶节距角βref,满足功率控制的要求,再加上权系数给出的桨距β

式中,maxVβ为当风速稳定在最大平均风速时对应的桨叶桨距角;minVβ为当风速稳定在最小平均风速时对应的桨叶桨距角。
设统一变化的桨叶桨距角为Δβ,各桨叶对应的桨距角权系数分别是k1、k2、k3,则可以通过数学表达式计算出各个桨叶单独变化时的桨距角变化量Δβ1、Δβ2、Δβ3。

各桨叶独立变化的桨距角为:

式中,βi为各桨叶单独变化时的桨距角;βref为统一给定的桨距角;ki为各桨叶对应的权系数,这里即为加速度权系数;Δβi为各桨叶单独变化时桨距角的变化量。
为了保证独立变桨控制输出与统一变桨控制输出一样,最终稳定在额定功率附近,必须时刻使桨距角变化量满足,权系数满足。
2.3 前馈补偿控制
前馈补偿控制的基本原理:当已知或者通过测量知道外部作用的条件下,施加一个与外部作用相反的控制量,目地是为了不让被控量受到变化,也就是说在外部作用和控制量的共同作用下,使偏差减小。采用前馈补偿控制,可以在保证系统稳定性的前提下使稳态误差减小,加强系统的跟随性能。
设按输入补偿的控制系统如图4。

图4 引入输入补偿的系统框图Fig.4 The introduction of input offset system block diagram
在上系统中,若E(s)=R(s)-C(s)=0,则完全跟随,即完全补偿,可得:

独立变桨距的电动执行机构是一种伺服跟随系统,通过液压装置或电机驱动系统实现,可以等效为一个一阶惯性环节:

式中:βτ为桨距角响应时间常数;β为实际桨距角;uβ为桨距角控制给定值。
在独立变桨距执行机构中加入按给定的前馈补偿如图5所示。

图5 输入给定的前馈补偿控制系统框图Fig.5 Given input feedforward compensation control system block diagram
3 仿真结果及分析
为了验证论文提出的控制策略的正确性和有效性,在Matlab/Simulink仿真系统中进行建模仿真,系统采用的是一台额定输出功率为2Mw的永磁同步发电机参数,主要技术参数如表l。

表1 永磁同步发电机模型参数表Tab.1 Model parameter table of permanent magnet synchronous generator
风电系统的运行状态主要由风速决定,所以仿真中风速的建立是比较重要且必不可少的。论文研究中,风速模型采用的是基于丹麦Risø 国家实验室建立的凯马(Kaimal) 频谱随机风速模型,如图6所示,随机风平均风速为14m/s,变化幅度为15%。结果如下:

图6 平均风速为14 m/s的随机风曲线Fig.6 Average wind curve with mean speed is14 m/s

图7 风力机的机械转矩输出曲线Fig.7 Wind turbine output mechanical torque
图7是基于前馈补偿加速度权系数独立变桨距控制下,风力发电机输出的机械转矩,随着风速的不断变化,各桨叶通过权系数分配调整自己的位置,最终使输出到发电机的机械转矩基本稳定在恒定值附近,使风电机组能够正常安全稳定地运行,保证对电能质量的要求。
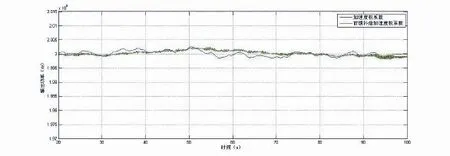
图8 输出功率曲线Fig.8 Curve of the out power
由图8可看出,基于前馈补偿加速度权系数独立变桨距控制下的功率输出相对加速度权系数独立变桨距同样都能稳定在额定功率附近,但是前者波动幅度和频率更小,对功率波动抑制的效果更好。随着时间的增加,控制器精度不断增强,表现出更好的稳定性。
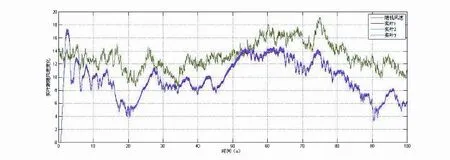
图9 桨叶跟随风速变化曲线Fig.9 Blade with wind speed change curve
图9是风力机桨叶跟随风速的变化情况,由仿真图可知,随着风速的变化,控制器通过各桨叶轴向气动力的变化幅度分配各桨叶加速度权系数,从而使桨叶调节桨距角的大小跟随风速的变化而变化,实现独立变桨距控制。
4 结论
论文采用永磁同步电机作为发电机,连接着风力机和电网侧,在加速度权系数分配控制算法上进行前馈补偿,通过比较得知,论文提出的该控制算法是正确的,具有可行性。在稳定发电机输出功率以及减小叶片载荷方面起到了很好的效果,同时各桨叶也能很好的跟随风速的变化而不断变化,桨叶拍打振荡减小,具有很好的工程实用价值。但是,该控制方法也有它的一些缺点,因为加速度传感器必须安装在桨叶上,这对大型风力发电机来说是一个很大的技术难题。
参考文献
[1] 姚兴佳,刘玥,郭庆鼎. 基于前馈补偿方位角权系数的分程独立变桨距控制研究[J]. 太阳能学报,2012,04:532-539. Yao Xingjia,Liu Yue,Guo Qingding. A control method for split range individual pitch based on feedforward azimuth angle weight number assignment [J]. Journal of solar energy,2012,532:532-539.
[2] 秦斌,郭百顺,朱万力,等. 基于支持向量机模糊权系数独立变桨距控制策略[A]. 中国自动化学会过程控制专业委员会.第25届中国过程控制会议论文集[C].中国自动化学会过程控制专业委员会:,2014:6. Qin Bin,Guo Baishun,Zhu Wanli,et al. The control strategy of independent variable pitch based on support vector machine weight coefficient[A]. TCPC. Proceedings of the 25th China process control[C]. TCPC:,2014:6.
[3] 叶杭冶.风力发电机组的控制技术[M ].北京:机械工业出版社,2007. Ye Hangzhi.Control strategies of wind turbine generators[M].Beijing:China Machine Press,2007 (in Chinese).
[4] Wai R J,Lin C Y,Chang Y R.Novel maximum power extraction algorithm for PSMG wind generation system[J].IET Electr Power Application,2007,1(2):275-283.
[5] 郭金东,赵栋利,林资旭,等.兆瓦级变速恒频风力发电机组控制系统[J].中国电机工程学报,2007,27(6):1-6. GuoJindong,ZhaoDongli,LinZixu,et a1.Research of the megawatt level variable speed constant frequency wind power unit control system[J].Proceedings of the CSEE,2007,27(6):1-6(in Chinese).
[6] 任丽娜,吕明月,刘爽爽,等. 基于蜂群算法优化的变桨距自抗扰控制器[J]. 新型工业化,2014,06:43-48. Ren Lina,Lv Mingyue,Liu Shuangshuang,et al. Based on the swarm algorithm to optimize the variable pitch ADRC[J]. The Journal of New Industrialization,2014,06: 43-48.
[7] 高峰,徐大平,吕跃刚.大型风力发电机组的前馈模糊PI变桨距控制.动力工程,2008,28(4):537-542. Gao Feng,Xu Da-ping,Lu Yue-gang. Feed Forward Fuzzy-PI Pitch-control for Large-scale Wind Turbines[J]. Journal of Power Engineering,2008,28(4):537-542.
[8] 张雷,李海东,李建林,等.基于LQR方法的风电机组变桨距控制的动态建模与仿真分析[J].太阳能学报,2008,29(7):781-785. Zhang Lei,Li Haidong,Li Jianlin,et al. Dynamic modeling and simulation of pitch control strategy for wind turbines based on LQR method[J]. Acta Energlac Solaris Sinica,2008,29(7): 781-785.
[9] H.D. Battista,R.J. Mantz,C.F.Christiansen. Dynamieal sliding mode Power control of wind driven induction generators[J]. IEEE Transaetions on Energy Conversion,2000,15(4):452-457.
[10] Vapnik V the nature of statistical learning theory[M].New York:Springer,1 995.
[11] 王欣,李胜刚,秦斌,等. 基于模糊支持向量机的风电场功率预测[J]. 新型工业化,2014,09:50-55. Wang Xin,Li Shenggang,Qin Bin,et al. Wind power prediction based on fuzzy support vector machine [J]. The Journal of New Industrialization,2014,09: 50-55.
[12] 廖勇,何金波,姚骏,等.基于变桨距和转矩动态控制的直驱永磁同步风力发电机功率平滑控[J].中国电机工程学报,2009,29(18):71-77. LiaoYong,HeJinbo,YaoJun,et a1.Power smoothing control strategy of direct-driven permanent magnet synchronous generator of wind turbine with pitch angle control and torque dynamic control[J].Proceedings of the CSEE,2009,18(29):71-77(in Chinese).
[13] 姚兴佳,张雅楠,郭庆鼎,等. 大型风电机组三维模糊控制器设计与仿真.中国电机工程学报,2009,29(26): 122-117. Yao Xingjia,Zhang Yanan,Guo Qingding et al. Large wind turbines three-dimensional fuzzy controller design and simulation. Proceedings of the CSEE,2009,29 (26) : 122-117.
[14] Kyoungsoo Ro,Hanho Choi. Application of neural network controller for maxilnum power extraction of a grid connected wind turbines system. Eleetrical Engineer,19,2005,88(12):45-53.
[15] Jianning Li,Hongye Su,Yibo Zhang,et al. Chattering Free Sliding Mode Control for Uncertain Discrete Time-Delay Singular Systems [J]. Asian Journal of Control,15(1): 260-269.
[16] Kazmi S M R,Goto H,Guo H J,et a1.A novel algorithm of fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems [J].IEEE Transactions on Industrial Electronics,2011,58(1):29-36.
[17] Parrella F. Online Support Vector Regression[D]. Genoa,Italy:University of Genoa,2007.
[18] Anca Hansen,Florin Iov,Poul Sorensen,et a1. Overall control strategy of Variable speed doubly-fed induction generator wind turbine [C]. Nordic Wind Power Conf. ,Gotebog,Sweden,2004.
DOI:10.3969/j.issn.2095-6649.2015.08.005
*基金项目:国家自然科学基金(61074067)
作者简介:范定成(1989-),男,湖南邵阳人,硕士研究生,主要研究方向:风力发电技术;秦斌(1963-),男,博士,研究方向:复杂系统建模与优化控制;姜学想,男,硕士研究生,主要研究方向:风力发电
A Control Method For Invidual Pitch Based on Feedforward Compensator Accelerated Speed Weight Number Assignment
FAN Ding-cheng, QIN Bin, JIANG Xue-xiang
(School of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou , 412007)
ABSTRACT:Wind power generation system has a natural wind speed of randomness, degeneration and the system nonlinear characteristics, so a control method for invidual pitch was proposed based on feedforward compensator accelerated speed weight number assignment. In order to realize the independent variable pitch control and each blade with wind speed varies, the acceleration weight coefficient assigned to control each blade individually. Then, according to the theory of feedforward compensation of knowledge to compensate the whole controlling process. The pitch control mode of permanent magnet direct-drive wind power system is built and simulated by MATLAB/Simulink simulation system. The simulation results show that not only the proposed strategy has such advantages as strong ability of rejecting chattering, well robust to the variation of parameter and fast response, but also in the stable system output power , at the same time, to realize the smooth change of each blade and to reduce wind turbine fatigue load and friction.
KEYWORDS:Wind turbine system; Variable pitch control; Feedforward compensator; Accelerated speed weight number

