深沟球轴承振动的灰自助评估

卢阳，时保吉，郭浩，李泽强

(1.洛阳轴研科技股份有限公司，河南 洛阳 471039；2.新乡职业技术学院，河南 新乡 453006)

轴承振动与其噪声密切相关[1]，长期以来一直受到相关领域的广泛重视。文献[2]介绍了一种基于滚动轴承缺陷探测的有限元振动分析方法。文献[3]研究了高速转子的结构振动分析模型。文献[4]建议进行振动监测与分析实例研究。但目前的研究大多未涉及乏信息领域，然而关于乏信息参数估计方面的问题越来越受到关注与重视，成为近年来系统科学领域研究的热点问题与前沿课题之一。

研究表明，轴承振动性能的趋势变化不明显，属于趋势规律与概率分布都未知的乏信息系统。下文基于乏信息中的灰自助融合与灰预测理论，建立深沟球轴承振动特征参数的动态灰自助频率函数，并对振动特征参数进行灰自助评估，从而为轴承振动性能的非线性动力学特性演变奠定理论基础。

1 乏信息动态评估模型

利用乏信息系统理论，结合自助法，利用灰自助融合和灰预测构建数学模型，并对深沟球轴承振动参数进行动态不确定度分析，以实现对深沟球轴承振动特征参数进行灰自助评估。

1.1 初步处理

假设深沟球轴承振动性能试验总共进行了R天，令Xr表示第r天所采集到的需要处理的振动试验数据，其中r=1,2,3,…,R，所以第r天进行数据处理的振动试验数据为

Xr=(xr(1),xr(2),…,xr(t),…,xr(N))，

(1)

式中：xr(t)为第r天t时刻的振动试验数据；N为第r天需要进行处理的数据个数。

1.2 灰自助融合

从Xr中取与t时刻紧邻的前h个数据(含时刻t的数据)，构成t时刻的滚动融合子序列向量为

Xrt={xrt(u)}，u=t-h+1,t-h+

2,…,t;t≥h，

(2)

式中：u为时刻；h为与t时刻紧邻的前h个数据(含t时刻的数据)，即滚动因子。

滚动融合评估的含义是用t时刻前的Xrt评估时刻t的振动属性状态。在t时刻，从Xrt中等概率可放回的随机抽取1个数据，抽取h次，获得一个自助样本，含h个数据。连续重复抽取B1次，得到B1个自助再抽样样本，用向量表示为

YrtBootstrap=(Yrt1,Yrt2,…,Yrtb,…,YrtB1)，

(3)

式中：Yrtb为第b个自助样本。且有

Yrtb={yrtb(u)}；b=1,2,…,B1，

(4)

式中：yrtb(u)为Yrtb中第u个自助再抽样数据。

由灰预测GM(1,1)，设Yrtb的一次累加生成序列向量为

(5)

再设均值生成序列向量为

Zrtb={zrtb(u)}={0.5xrtb(u)+0.5xrtb(u-

1)}，u=t-h+2,t-h+3,…,t，

(6)

在初始条件xrtb(t-h+1)=yrtb(t-h+1)下，问题的最小二乘法为

e-crtb1j+crtb2/crtb1，j=t-1,t，

(7)

(crtb1,crtb2)T=(DTD)-1DTYrtbT，

u=t-h+2,t-h+3,…,t-1,t，

(8)

D=(-Zrtb,I)T，

(9)

I=(1,1,…，1)。

(10)

时刻ω=t+1的预测值可以表示为

(11)

其中B1个数据构成的序列向量为

(12)

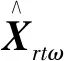
Frtω=Fω(xrt)，

(13)

式中:Frtω为灰自助频率函数。

2 振动特征参数的乏信息过程动态评估分析

设显著性水平为α∈ [0,1] ，则置信水平为

P=(1-α)×100%。

(14)

在时刻t，置信水平P下，振动属性参数真值的估计区间为

[XrtL,XrtU]=[XrtL(ω),XrtU(ω)]=

(15)

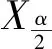
XrtL为估计区间下边界值；XrtU为估计区间上边界值。

参数指标XrtL和XrtU用来描述振动属性参数在时刻t瞬态波动的极小值和极大值。

定义ω时刻振动属性参数的动态不确定度为

Urt=Urt(ω)=XrtU-XrtL，

(16)

式中：Urt为在置信水平P下估计的不确定度，即动态不确定度。

动态不确定度随时间序列变化，具有时间过程与动态的变化特性，其不同于以往的经典统计方法研究静态不确定度。文中虽然使用频数的概念，但实际并未涉及原始振动数据序列Xr的概率分布问题。这表明灰自助GBM(1,1)不依赖任何概率分布。

由 [XrtL,XrtU]和Urt的定义可得，在ω时刻，置信水平P越大，则Urt越大。若P=100%，则Urt可以得到最大值。但必须考虑一个问题，即Urt越大，[XrtL,XrtU]越偏离真值，进而估计结果就越失真。因此，给出一个条件

Urmean=Urmean(h,B1,P)=

(17)

式中：Urmean为平均不确定度。Urmean是一个统计量，可以作为振动属性参数随机波动状态的统计评价标准。Urmean越小，振动属性参数的波动范围越小，估计真值就越稳定，故必须结合具体的研究对象合理选择h，B1和P这3个参数。

3 试验结果与分析

文中引用的深沟球轴承振动加速度的试验数据(m/s2)来源于某研究所。某型号深沟球轴承在轴向载荷Fa=50 N，转速n=1 000 r/min下连续运行46 d。

对振动试验数据进行按天分段处理，选取每天前100个数据(N=100)用于分析，整个试验过程将有1 000个(R=10)原始振动数据。深沟球轴承振动试验的原始数据序列如图1所示。

图1 深沟球轴承振动试验数据

从轴承振动试验数据可以发现，在整个试验过程中，振动性能具有强烈的波动和趋势变化，属于概率分布及趋势规律均未知的乏信息系统。为了实现对深沟球轴承振动性能的灰自助评估，利用灰自助评估模型对轴承振动试验数据进行处理与分析。

参数h的选择很重要，h太大，评估时将包含过多的旧信息，影响评估的可靠度，并且降低评估速度，占用过多的计算机内存，不利于在线评估和控制；h太小，不利于自助再抽样，也直接影响评估的可靠度。灰色系统理论的灰预测GM(1,1)模型要求h的最小值为3，灰自助法中取h=4～8，此处选取h=4。

设显著性水平α=0.05，置信水平P=1-α=0.95，选取B1=1 000。当1≤r≤10，4≤t≤100时，利用深沟球轴承振动性能的灰自助评估模型，分别计算振动属性参数真值的估计区间[XrtL,XrtU]，计算动态不确定度Urt，分别绘制第1天和第2天的原始振动数据与估计区间 [XrtL,XrtU]的包络图和Urt随t时刻的变化图，如图2、图3所示。

由图2、图3可知，深沟球轴承的振动数据被完美地包络在估计区间 [XrtL,XrtU]之中，动态不确定度可以准确描述深沟球轴承基于振动时间点的数据波动状况，平均不确定度可以定量而准确地描述深沟球轴承基于振动时间段的数据波动及离散状况。平均不确定度越小，表明振动数据在当前时间段离散程度越小，稳定性越好；平均不确定度越大，表明振动数据在当前时间段离散程度越大，稳定性越差。

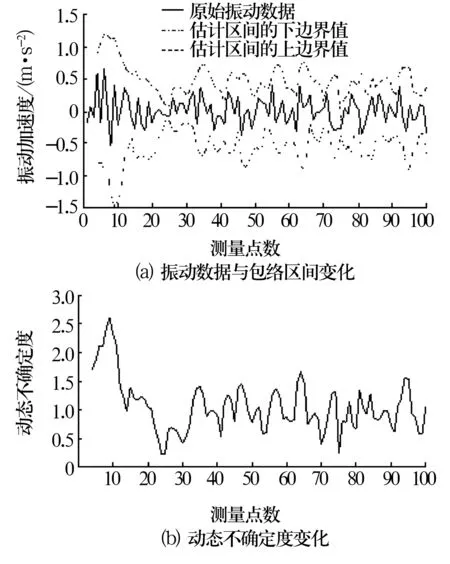
图2 第1天轴承振动数据动态不确定度变化图

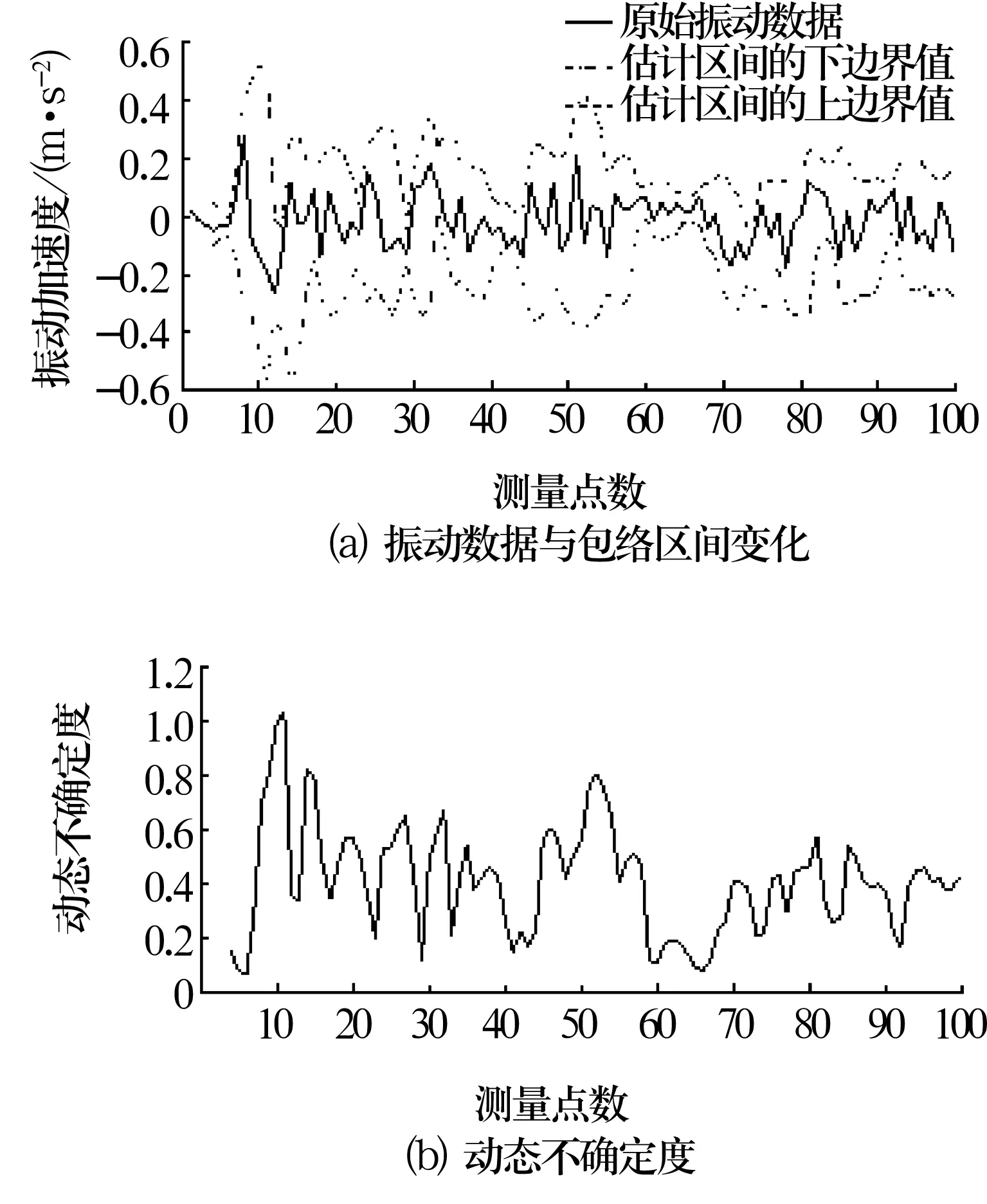
图3 第2天轴承振动数据动态不确定度变化图

计算深沟球轴承每天振动数据的平均不确定度Urmean，绘制Urmean随测量天数的变化图，如图4所示。

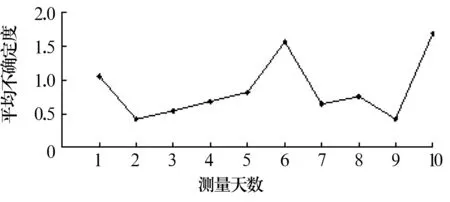
图4 轴承振动平均不确定度变化图

由图可知，试验中深沟球轴承第1天、第6天和第10天振动数据的平均不确定度较大，表明轴承振动处于非平稳状态。

4 结论

基于乏信息中的灰自助融合与灰预测理论，建立深沟球轴承振动特征参数的动态灰自助频率函数，并以此函数为基础，对深沟球轴承振动特征参数进行了灰自助评估，结果表明：

(1)基于振动时间点的动态不确定度可以准确地描述深沟球轴承基于振动时间点的数据波动状况。

(2)基于振动时间段的平均不确定度可以定量而准确地描述轴承基于振动时间段的数据波动及离散状况，且试验结果与计算结果非常接近，满足工程要求。