多因素分离过程蒙特卡罗仿真平台设计

李慧通，赵 阳

（哈尔滨工业大学航天学院，黑龙江哈尔滨150001）

多因素分离过程蒙特卡罗仿真平台设计

李慧通，赵 阳

（哈尔滨工业大学航天学院，黑龙江哈尔滨150001）

火箭和导弹等运载工具在飞行过程中涉及多种分离，分离过程出现问题会导致整个任务的失败。分离过程中分离体受到多种干扰因素和误差的影响，而靶场试验次数有限，无法得到多因素对分离过程的综合影响。设计了通用型的分离模型，建立包含多种力和干扰的分离载荷库，基于蒙特卡罗随机打靶技术，能够对多种分离过程进行打靶分析，得到多因素干扰的影响情况。对某导弹头罩分离过程进行了蒙特卡罗打靶仿真，得到了在多种偏差因素下分离体的运动范围。

仿真；蒙特卡罗方法；导弹头罩分离

0 引 言

在火箭和导弹发射过程中，将已完成预定工作而且在继续飞行中无用的部分分离并抛掉，可以改善飞行器后续飞行的质量特性，极大地提高运载能力。发射过程中飞行器一般经历若干次分离，包括头罩分离、级间分离、底罩分离、有效载荷分离等，分离方案变化大，分离过程受力复杂，如果针对每种分离情况开发仿真软件则周期长、费用高。不同分离方案的分离过程不确定因素多，分离体受力和受干扰复杂，干扰对分离过程的综合影响规律难以确定，很难通过几次实验就能找到分离的极限状态，过去一般都是靠科研人员的经验来进行估计和估算，这对分离机构的设计以及分离故障的排除带来了不便。因此亟待于构建一个通用型的分离仿真平台，能够针对现阶段两体纵向分离过程进行仿真，并且针对多种干扰因素进行打靶仿真，供科研设计人员对仿真结果进行统计学分析。

目前，国内外学者对偏差对分离的影响进行了一系列研究［18］，分离过程中，各种影响因素耦合程度高，无法通过单因素仿真实验确切得到多种影响因素下分离的极端情况和分离体运动范围，通过蒙特卡罗随机多次打靶则能较好地得到分离体运动分布范围。文献［9］用蒙特卡罗打靶方法对大气层内高超音速级间分离进行了研究，分析了随机偏差对分离运动的影响。文献［10］对微型导弹命中精度进行了蒙特卡罗打靶仿真研究，分析了多种干扰因素对导弹命中精度的影响。

对于飞行器动力学仿真和分离仿真平台的开发国内外学者也进行了较多研究［11-17］，文献［18］对火箭飞行过程的运动和受力进行仿真分析中，得到火箭飞行过程中位置、速度、加速度和火箭各子结构相互间的作用力，以及级间力在火箭飞行过程中的变化规律。文献［19］则对运载火箭在运输和发射过程中所受到的载荷环境进行了研究，开发了具有一定通用性的大型运载火箭载荷仿真软件。

现阶段所设计的分离仿真软件对于不同分离方案的通用性不强，对于多种偏差因素考虑不够全面。本文基于蒙特卡罗打靶技术设计了高通用性的分离仿真软件，能够对多种分离方案进行仿真分析。本文最后对头罩分离过程多种影响因素进行随机蒙特卡罗打靶仿真，确定需要打靶的某些参数及数值上下限后，通过多次随机打靶得到头罩分离极限分布情况和打靶的数据结果，供科研人员参考分析。

1 分离动力学模型

通用的两体纵向分离仿真平台必须保证实现对多种分离方案的仿真支持，包括底罩分离、头罩分离、级间分离、有效载荷分离等。这就要求分离模型具有通用性，并且需要通用的力库供模型调用。

1.1 坐标系设计

分离过程中涉及到的坐标系包括惯性坐标系、弹体坐标系、速度坐标系和质心坐标系。

惯性坐标系（O－XYZ）：以发射点为坐标原点O，位于大地或者大海表面，Y轴方向指向正上方，X轴为水平方向，指向与弹体坐标系X轴成锐角，Z轴与X轴、Y轴构成右手坐标系。惯性系主要用于输入分离初始运动状态。

弹体坐标系（Ot－XtYtZt）：原点Ot设为飞行器顶端理论顶点处，理论顶点为整流罩顶端椎体的切线形成的曲面在空间的交汇点。Xt轴沿弹体纵轴指向弹头的正方向，也就是导弹的对称轴，Yt轴在导弹主对称平面内，即在发射的瞬时与惯性坐标系XOY平面重合，Zt轴与Xt轴、Yt轴构成右手坐标系。弹体坐标系原点位置不会随燃料的消耗而改变，主要用于分离初始受力参数的输入。

质心坐标系（Oc－XcYcZc）：原点为分离体的质心，Xc轴平行于弹体的对称轴，Yc轴指向在分离前与弹体坐标系Yt轴的方向相同，Zc轴与Xc轴、Yc轴构成右手坐标系。主要用于分离后分离体运动计算。

速度坐标系（Ov－XvYvZv）：原点位于分离体质心，Xv轴沿分离体的飞行速度方向，Yv在分离体纵对称平面内，垂直于Xv轴，当速度矢量为水平时指向上方，Zv轴与Xv轴、Yv轴构成右手坐标系。主要用于分离气动力的计算。

1.2 通用模型设计

设分离体所受外载荷为F（Fx、Fy、Fz），外力矩为M（Mx、My、Mz），分离体质量为m，转动惯量与惯量积为J（Jx，Jy，Jz，Jxy，Jxz，Jyz），分离体在惯性坐标系下位移变化为r（rx，ry，rz），转动角速度为ω（ωx，ωy，ωz）。6自由度欧拉方程表示为

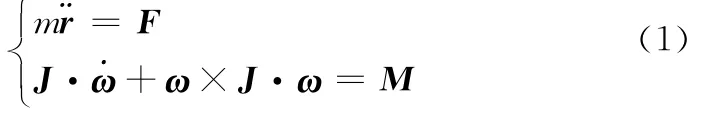
本文采用的欧拉角按照Z－Y－X顺序旋转，按照欧拉角的定义和欧拉角与角速度的相互关系可以得到体角速度（ωxωyωz）与欧拉角速度（）关系为

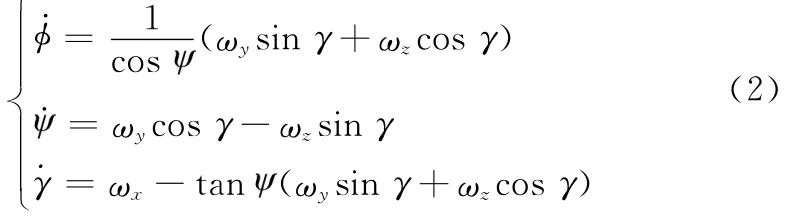
由于分离过程中，受到多种外力及干扰因素的影响，为了通用性地表示多种力和干扰，本软件平台设置了力库供使用者调用，如图1所示。

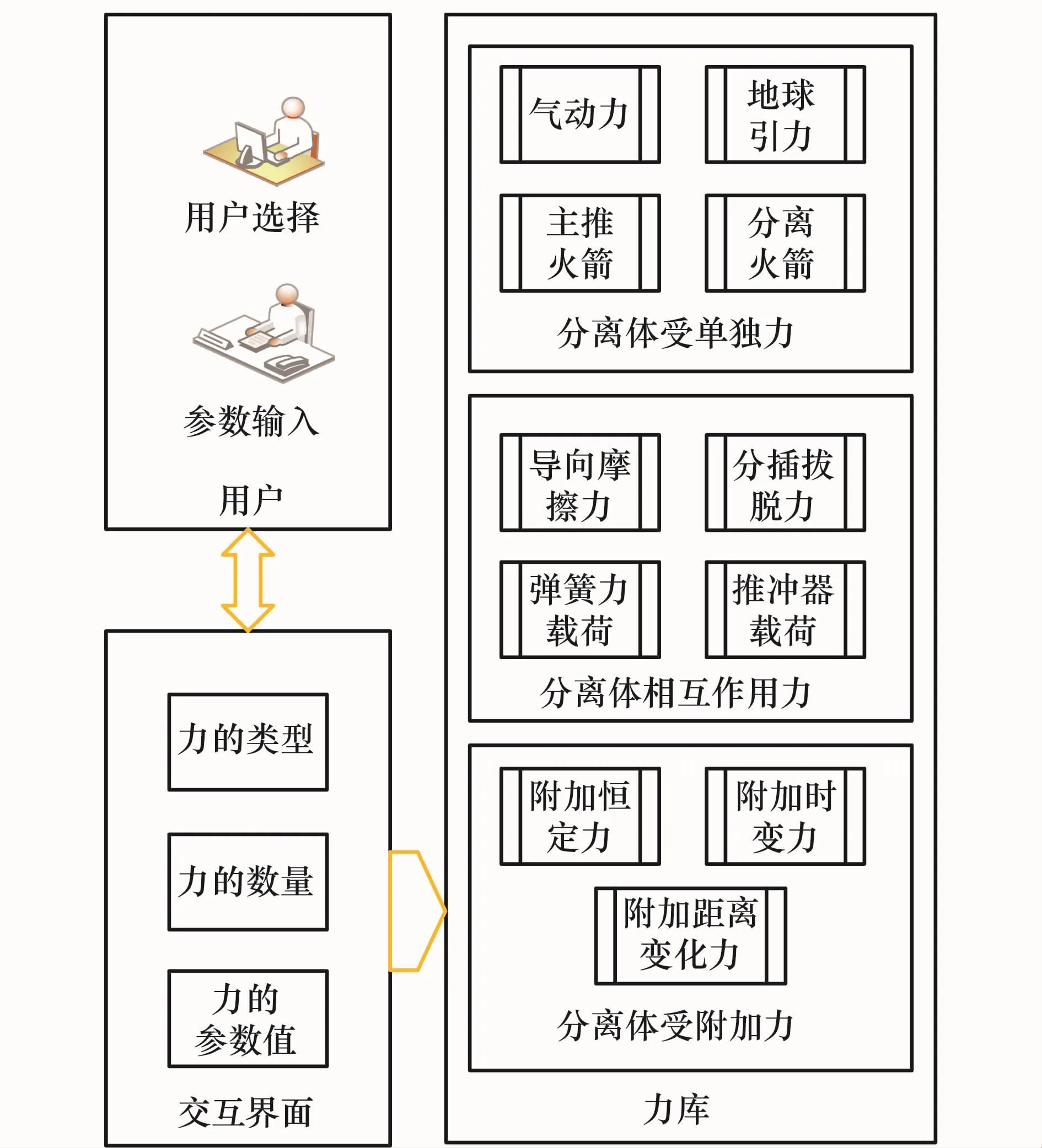
图1 分离力库设计

力库包含3种类型的力，包括分离体所受单独力、分离体相互作用力和附加力。每种类型的力最多可添加100个，能满足现阶段几乎所有二体纵向分离仿真需求。

（1）分离体所受单独力

分离体单独受力包括气动力、地球引力、主火箭推力和分离火箭推力，这类力仅单独分离体受力，不考虑其对另外一个分离体的运动的影响。

（2）分离体相互作用力

分离体相互作用力包括导向摩擦力、分插拔脱力、弹簧力和推冲器力，这类力对上下级分离体都有作用力，大小相等，方向相反。

（3）附加力

附加力包括附加恒定力、附加时变力和附加随距离变化的力。附加恒定力的大小和弹体系下力作用方向在分离过程中不发生变化；附加时变力的大小和方向随分离时间变化而变化，通过对关键点力的值进行一阶拉格朗日插值得到分离任意时刻力的大小和方向；附加随距离变化的力是随着分离体之间距离变化而变化的力，同样通过一阶插值得到任意分离距离力的大小和方向。对于未知的干扰和分离力，附加力可以很好地进行模拟，比如分离体之间的空气负压力就可以简化为随分离距离变化的力，这样对于将来新的分离方案可以进行仿真。

1.3 干扰因素分析

分离过程包括底罩分离、头罩分离、整流罩分离、级间分离、有效载荷分离等，所涉及到的高度范围从海拔十几米到几百千米，分离环境复杂，需要考虑多种干扰因素。所有的干扰因素和分离体参数都要在打靶过程中考虑。

质量几何偏差：在飞行器制造过程中会出现质量和转动惯量偏差，质心位置也可能有一定的偏移，在飞行过程中，随着燃料消耗，相关质心质量参数也会与理论值出现偏差。

初始运动偏差：分离体分离时刻的初始运动参数和转动参数可能存在一定的偏差。特别是考虑气动力时，分离时组合体初始姿态角度误差对分离体后续运动影响很大。

气动系数偏差：分离过程流场变化比较复杂，气动系数具有高度非线性，很难得到准确的气动系数模型，平台采用一阶插值方法得到气动系数曲线，并且软件平台设置气动系数偏差百分比输入接口。

主火箭偏差：主火箭的推力作用点可能存在横移，推力线方向和导弹纵轴可能存在一定夹角，这对分离过程有较大影响，推力值大小也有一定偏差，需设置主火箭推力偏差量接口，在软件平台中进行详细考虑。

分离火箭偏差：分离火箭推力实际值与理论值存在偏差，开机关机时间也有一定的不确定性，开机时推力值无法立即达到理论值，关机后也会存在后效推力，这些在打靶过程中都需要考虑。

2 仿真平台设计

2.1 平台总体结构

平台需要良好的人际交互界面，方便科研人员使用。平台界面采用Visio Studio分区架构形式，界面直观，易于操作和显示。主界面如图2所示。

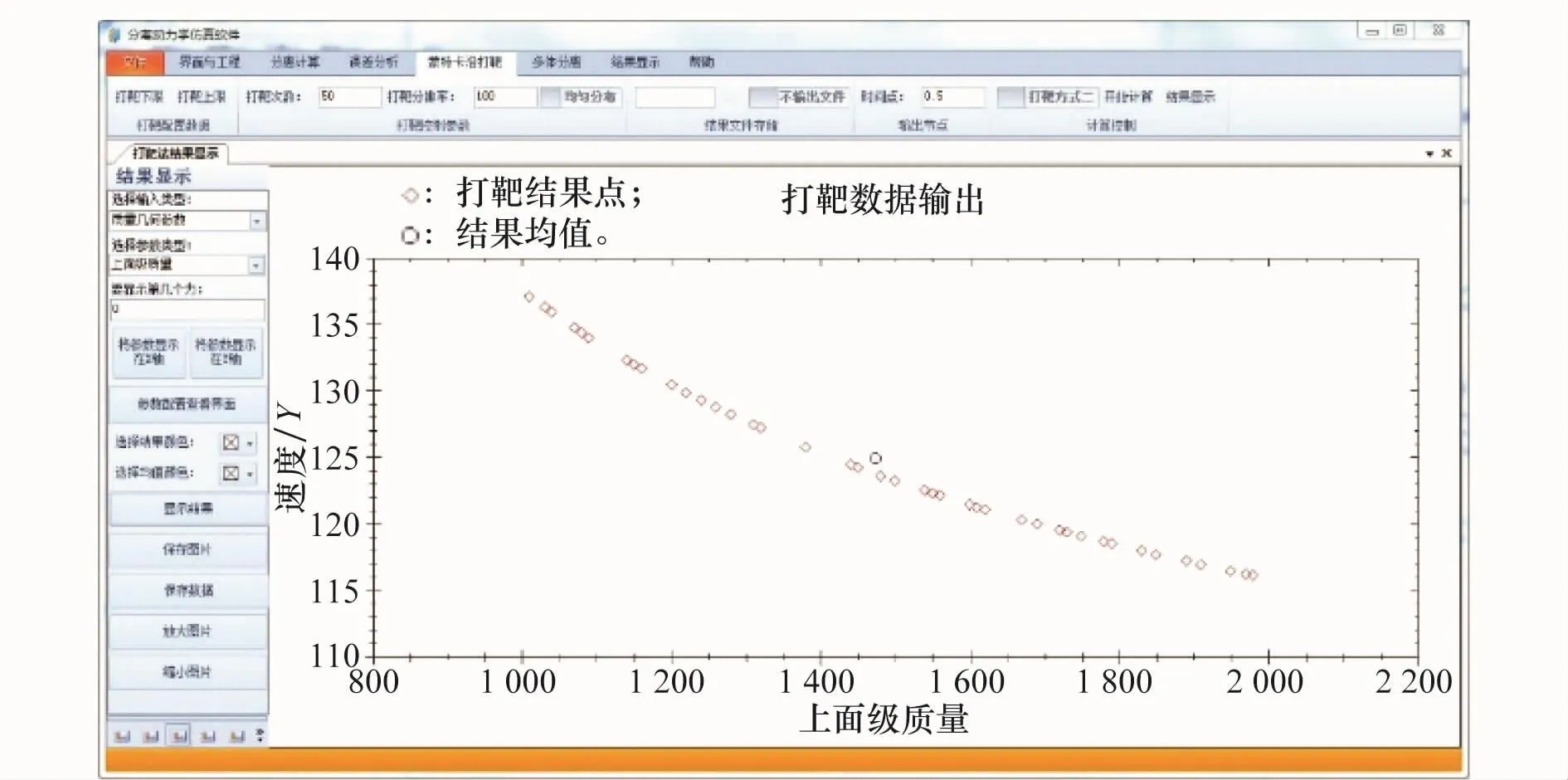
图2 平台界面

动力学软件的总体结构对软件系统的总体功能和系统的可维护性等方面有着至关重要的作用。分离过程蒙特卡罗打靶仿真平台采用现阶段动力学分析软件常用的前处理、中间分析以及后处理结果输出3大模块划分形式，如此划分使平台功能清晰，易于用户使用和进行软件维护。其平台架构如图3所示。

图3 打靶仿真平台架构图

用户通过前处理模块输入分离建模相关参数、分离体受力参数、相关参数偏差量以及打靶仿真控制参数，平台将数据传输到打靶处理模块进行多次循环打靶计算，将得到的结果送到后处理模块进行结果输出，根据用户的命令进行数据分析以及绘图显示。

2.2 打靶设计方案

在打靶仿真中，需要生成随机数，因为现阶段无法得到真正的随机数，一般采用取中法、位移法、乘同余法、混合同余法等获取伪随机数代替。本文采用混合同余法生成伪均匀分布的随机数，该方法对初值的依赖较小，产生的随机数列的性质较好，稳定性也比较好［20］。

用户设置随机数生成范围边界m和n，则在m～n的范围内采用混合同余法生成某随机数p。假设某参数的上边界值为aup，下边界值为adown，则生成的随机抽样值为

生成随机抽样值后代入分离动力学仿真部分进行仿真求解，并多次重复这个过程。利用蒙特卡罗方法进行分离过程仿真的基本步骤：

步骤1 根据用户输入参数，建立经过简化的分离过程动力学模型；

步骤2 生成均服从均匀分布的随机抽样值，这样得到的结果更为保守；

步骤3 将抽样值加载到分离动力学仿真模型，并进行仿真计算；

步骤4 重复进行步骤2和步骤3，多次进行仿真，即可获得分离运动过程的子样集；

步骤5 对多次随机仿真结果进行分析和输出。

根据以上基本步骤可以得到打靶仿真流程如图4所示。打靶仿真流程可分为前处理、打靶计算和后处理3部分，对应平台架构的前处理模块、打靶处理模块和后处理模块。

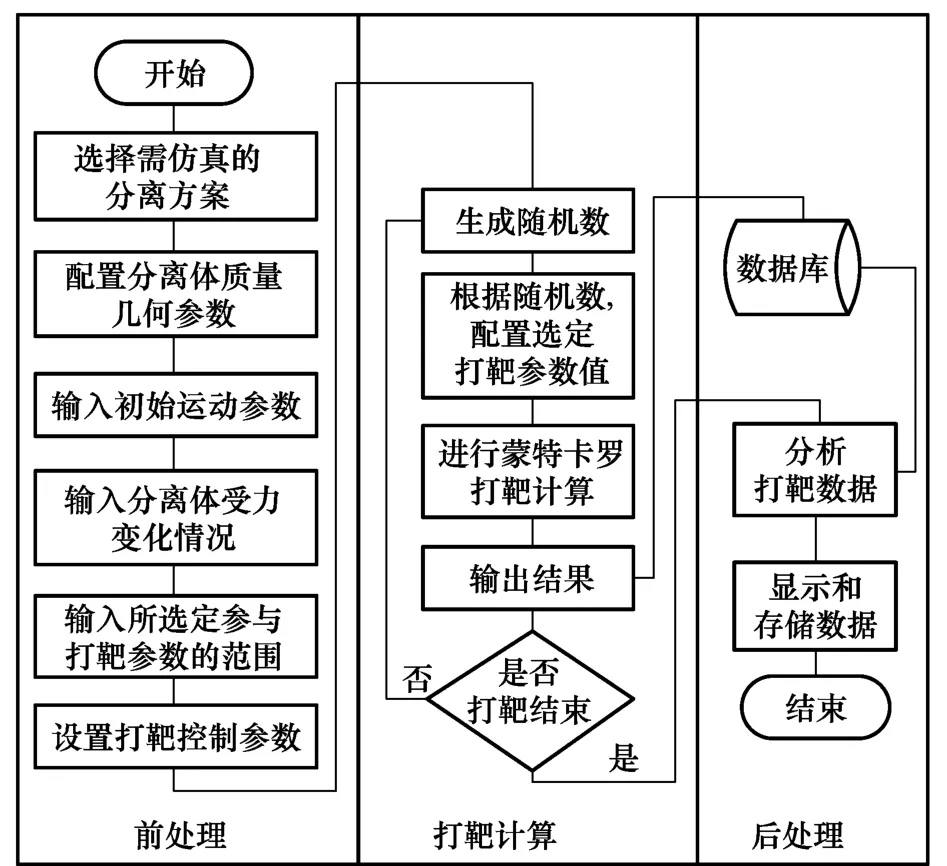
图4 打靶仿真流程图

2.3 平台描述及实现

多因素分离过程蒙特卡罗仿真平台可划分为3大模块，包括前处理模块、打靶处理模块和后处理模块。

2.3.1 前处理模块

前处理模块功能包括仿真管理参数、模型参数配置、干扰参数配置以及打靶参数控制4大部分，如图5所示。主要功能为输入仿真参数和打靶控制参数。

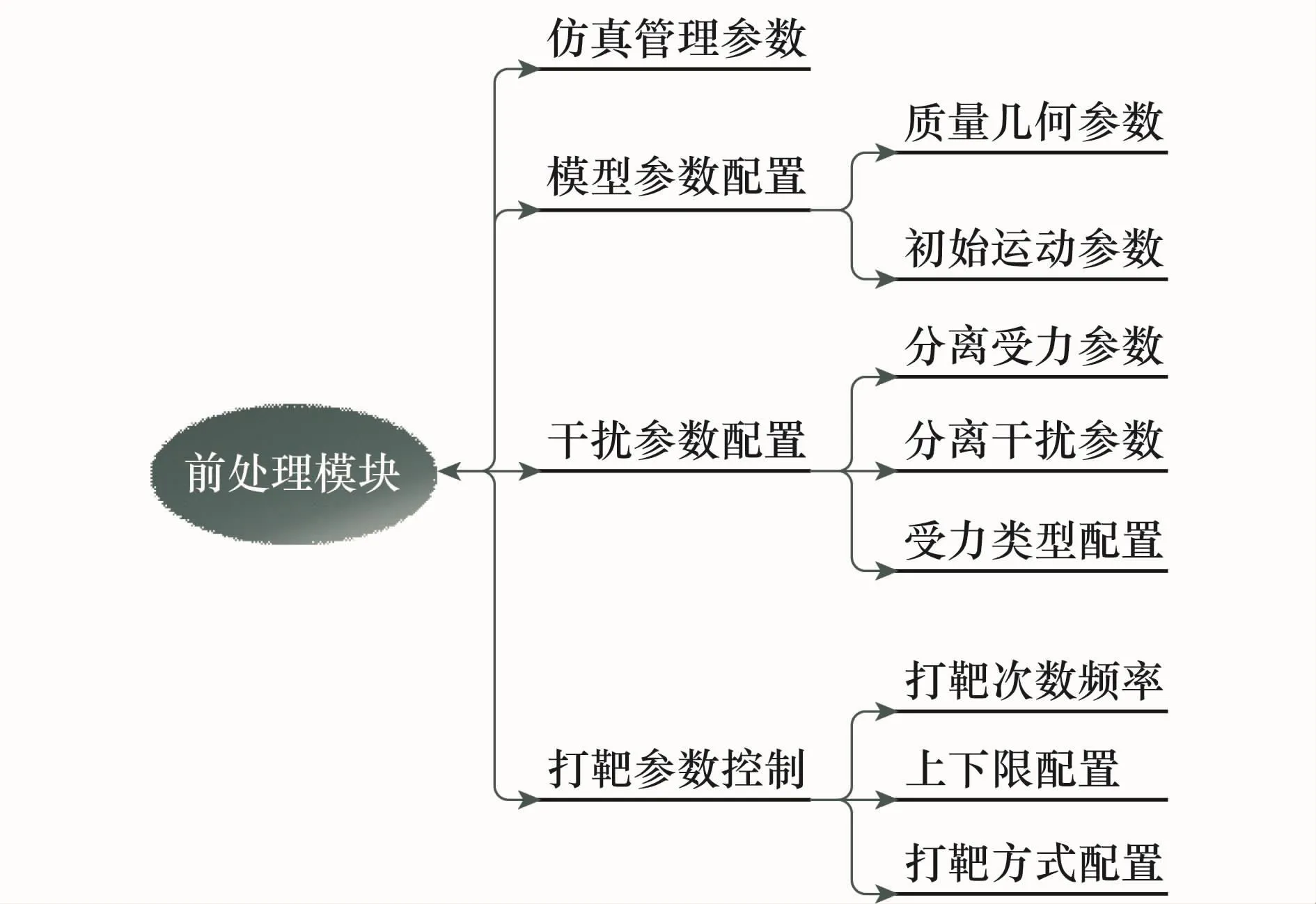
图5 前处理模块功能划分

仿真管理参数功能为输入积分步长和积分时间等。模型参数配置包括质量几何参数以及初始运动参数，主要功能根据用户输入的参数构建分离动力学通用模型。

干扰参数配置包括分离体受力参数、分离体干扰参数以及受力类型配置。主要功能为根据用户的输入构建分离体受力和受外界干扰的数学仿真模型；包括气动力、主火箭推力、分离火箭推力、分插拔脱力、空气负压力、推冲器力等，根据用户的选择和输入的参数生成分离体受力模型。

打靶参数控制包括打靶次数频率、上下限配置和打靶方式配置。主要功能为控制打靶次数和流程，由用户选定需要打靶的某些参数和限定相关参数的打靶范围，并进对随机抽样值的生成进行选择。

2.3.2 打靶处理模块

打靶处理模块包括模型求解模块、动力学模型、随机数生成和打靶流程控制4部分，如图6所示。动力学模型根据前处理模块传递的数据自动生成，并送入模型求解模块进行积分求解运算。随机数生成模块根据用户的选择生成均匀分布随机数。打靶流程控制监控打靶计算流程，根据需要停止打靶仿真，并将结果数据打包传递给后处理模块。

图6 打靶处理模块功能划分

2.3.3 后处理模块

后处理模块包括统计学分析、结果显示和结果存储3部分，如图7所示。主要功能为分析打靶数据和向用户直观的展现打靶结果，便于用户分析。

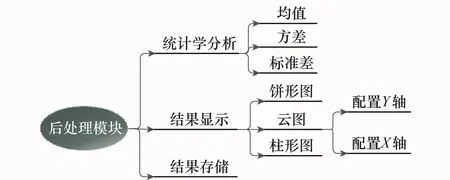
图7 后处理模块功能划分

统计学分析模块对用户选定的需要输出的参数进行均值、方差和标准差的处理。结果显示模块根据用户的选择输出打靶结果的云图、饼形图和柱形图。结果存储模块将打靶结果进行存储，以txt文档形式保存，便于阅读，供以后调用分析。

3 头罩分离算例分析

潜射导弹一般带有外头罩保护弹头以避免海水冲击的损坏，当导弹发射后距离海面一定高度后，外头罩工作任务结束，需要将外头罩抛离导弹，以减少后续飞行过程中的弹体质量。

分离体上面级为头罩，下面级为弹体，弹体下部安装主推火箭，头罩侧面安装4枚分离火箭，头罩和弹体之间用爆炸螺栓连接，分离体之间有导向机构和控制线缆插头。由于分离是在低海拔稠密大气层中分离，所以需要考虑气动力对分离过程的影响。头罩分离示意图如图8所示。

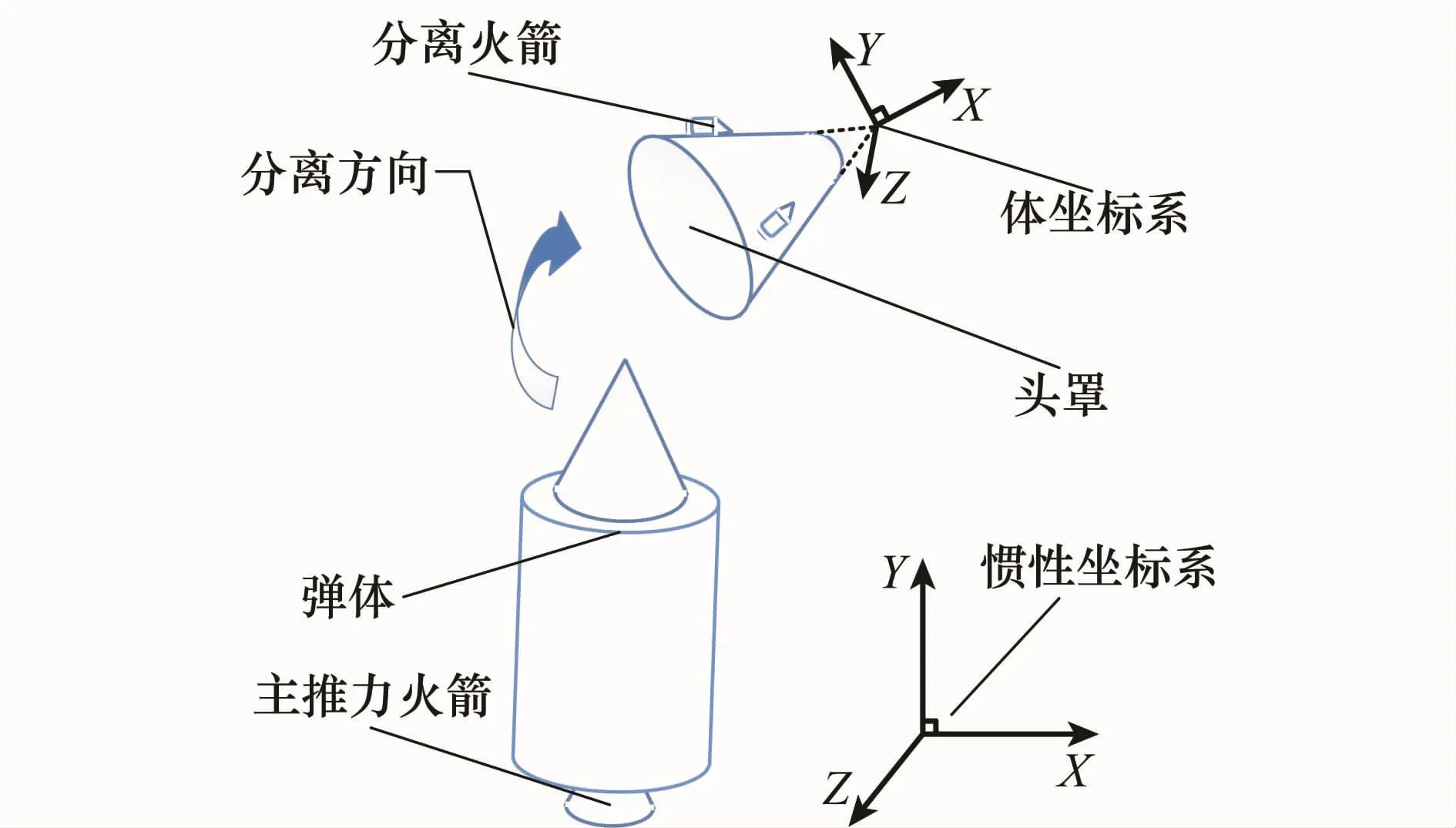
图8 头罩分离示意图

头罩主要受气动力、分离火箭力、空气负压力、分插拔脱力和分离机构冲击力的影响；弹体主要受气动力、空气负压力、分插拔脱力、主火箭力和分离机构的冲击力影响。

头罩上安装4枚分离火箭，以90°夹角沿头罩圆周均匀分布，推力线与导弹中轴线呈35°夹角。弹体坐标系下分离火箭安装形式如图9所示。

图9 分离火箭安装示意图

头罩在分离阶段受力情况为

下面级导弹在分离阶段受力为

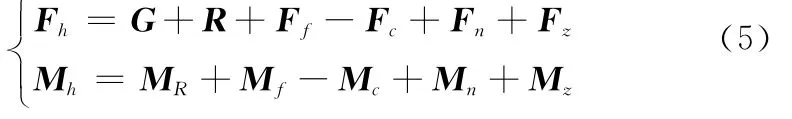
式中，G为地球引力；R为气动力；Fi（i＝1，2，3，4）为4个分离火箭的推力矢量；Ff为分插拔脱力；Fc为爆炸螺栓冲击力；Fn为空气负压力；Fz为下面级主火箭推力。MR为气动力矩；Mi（i＝1，2，3，4）为4个分离火箭的推力力矩；Mf为分插拔脱力矩；Mc为爆炸螺栓冲击力矩；Mn为空气负压力矩；Mz为下面级主火箭推力矩。

在实际飞行过程中，导弹的飞行状态比较复杂，受到的影响因素很多，对分离体进行打靶分析时必须首先进行一定得简化和模型假设。

（1）分离体看作刚体，不考虑其形变对气动参数的影响；

（2）由于分离时间短暂，不考虑分离时横风对分离过程的影响；

（3）不考虑分离火箭的喷流对下面级分离体流场的影响；

（4）分离火箭推力假定为恒定力，将火箭推力上升段和下降段的变力和中间的恒定推力在保证总冲量一致的前提下整合，简化为一恒定推力；

（5）分离机构的冲击力简化为一短时间的恒定力；

（6）分离运动仿真不考虑地球自转和地球曲率的影响。

3.1 计算参数配置

本文研究的火箭头罩分离由于不同的设计方案，质量特性变化较大，在1 000～1 500 kg范围内浮动，同时转动惯量也同时出现变化，质心位置由于制造误差，也会产生一定范围内的偏差。头罩质量几何偏差如表1所示。

表1 头罩质量几何特性表

分离火箭在实际情况下关机时间会出现误差，不可能在指令发出的精确时间点关机，将关机分离火箭推力下降段简化为一个短时间的恒定力，这个恒定力和推力下降段冲量一致。分离火箭的推力为30 k N，火箭的开关机时刻表如表2所示。

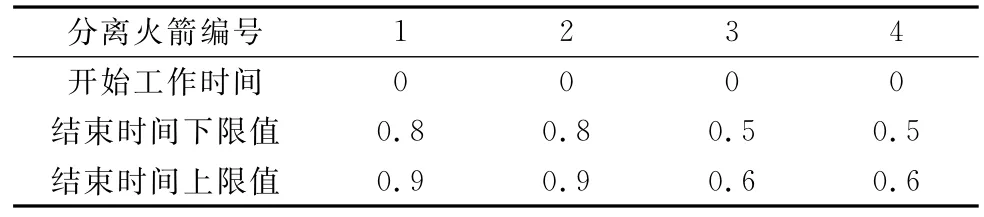
表2 分离火箭开关机时刻表

3.2 仿真计算结果

500次打靶计算后得到大量结果数据，进行分析并且绘图输出，由于本文的篇幅有限，本文列举部分具有代表性的结果图。本文取分离后0.6 s时间节点进行分析，结果云图中黑色球形块为打靶结果值。

在惯性坐标系下，头罩X方向、Y方向和Z方向位置分布图如图10所示，X方向位置在－2～2 m之间，Y方向高度在1 072～1 080 m之间，Z方向在－1～3 m之间。在Y方向上头罩的散布范围比X方向和Z方向要大。

根据打靶结果分析，头罩和弹体质心的距离与头罩质量变化相关性较大，如图11所示，随着上面级质量的增加，分离距离相应减少，质心距离在12～18 m之间。

质心相对距离与分离火箭3以及分离火箭4的关机时间关系如图12所示，分离后0.6 s时质心相对距离变化范围为12～18 m之间。此时分离火箭1和分离火箭2仍在工作。

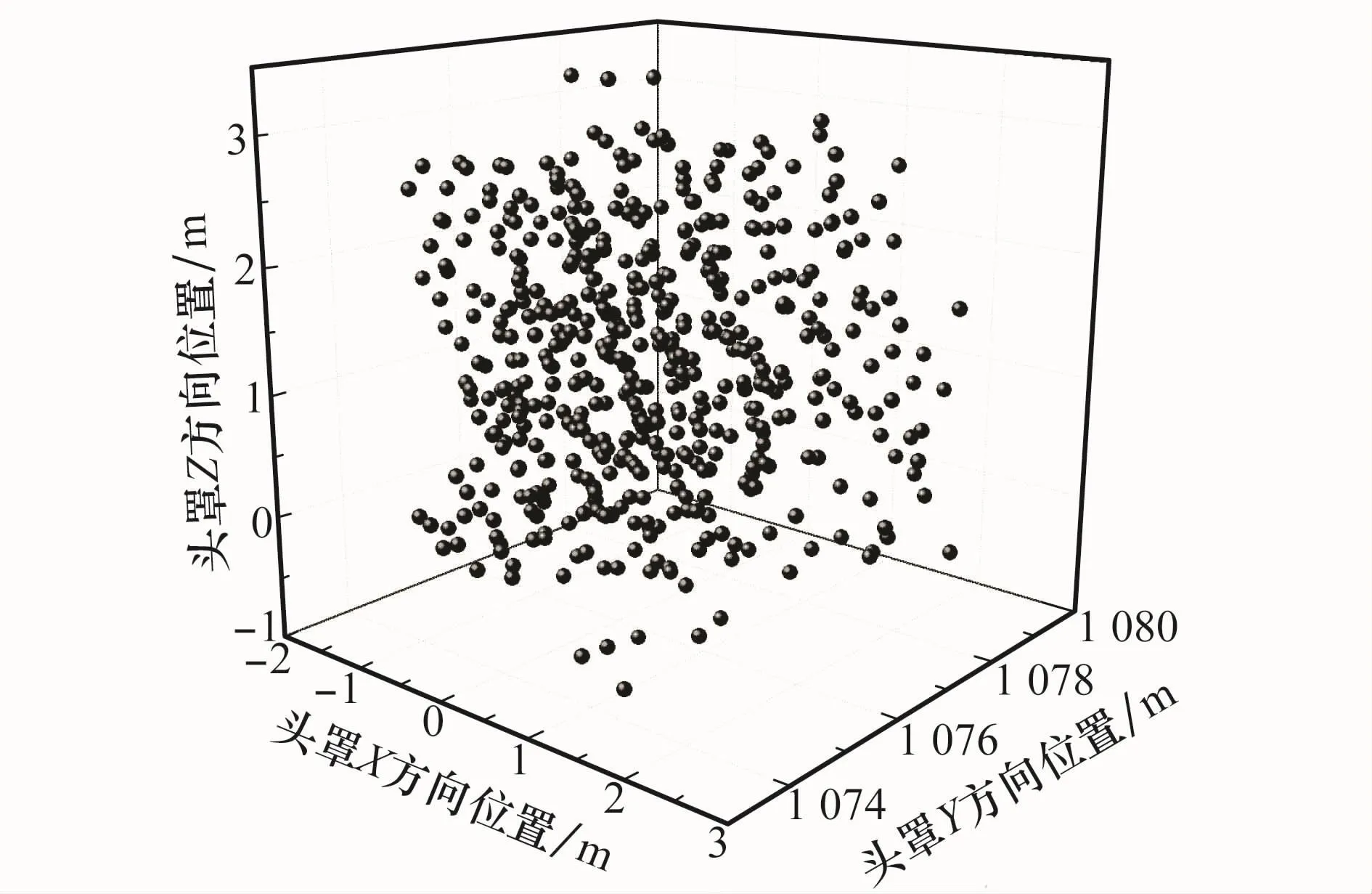
图10 头罩位置打靶结果图

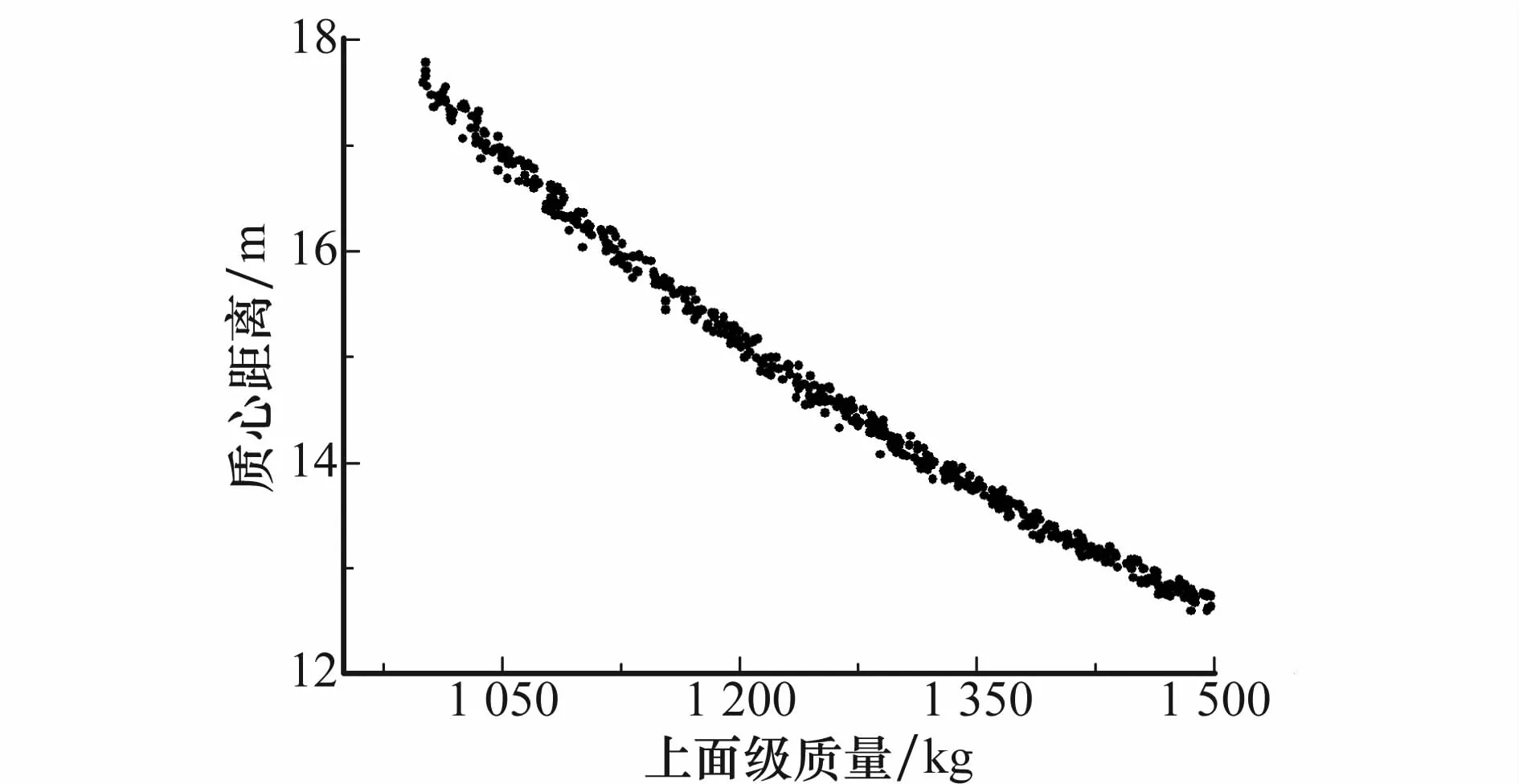
图11 质心相对距离与上面级质量关系图

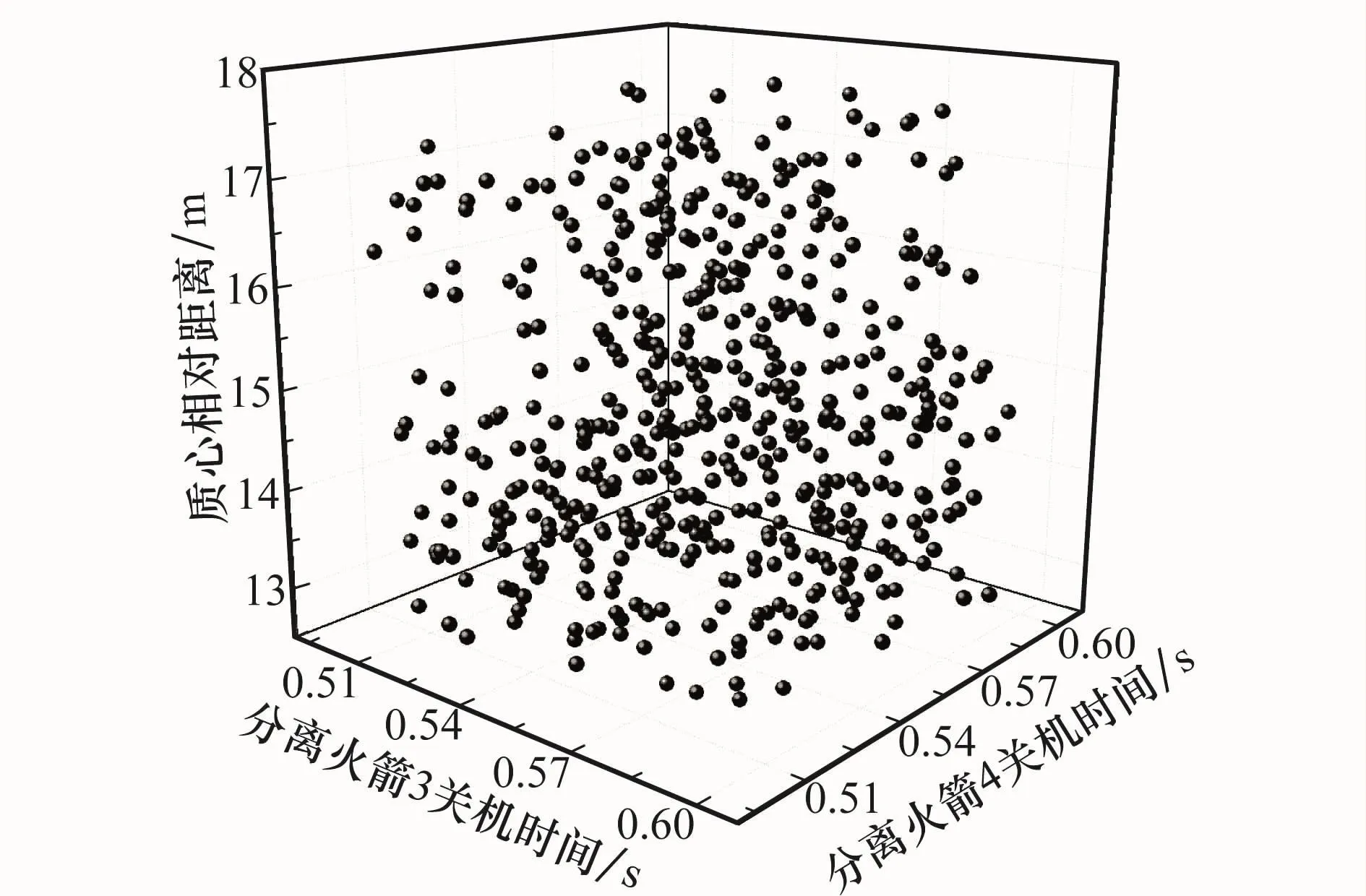
图12 质心相对距离与分离火箭工作时间关系图

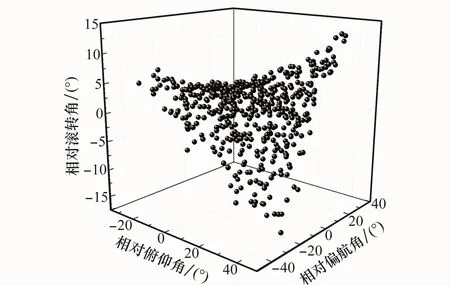
图13 分离体相对角度分布情况

由图13可知，头罩分离到0.6 s时，头罩和下面级导弹的相对俯仰角在－30°～40°之间，相对滚转角在－15°～15°之间，相对偏航角在－40°～40°之间。

由图14可知，相对俯仰角度与质心Y方向的位置关联性较大，随着质心位置在弹体系下由－0.1 m过渡到0.1 m，相对俯仰角由－30°增加到40°。

图14 质心位置Y方向与相对俯仰角关系图

由于本文篇幅有限，无法给出更多的结果图，通过打靶计算可以得到分离后头罩和下面级火箭的分布范围，得到分离结果和偏差量的对应关系，供给科研人员进行分析和验证。

4 结 论

本文设计的通用分离蒙特卡罗打靶平台通用性强，能够仿真多种分离方案，考虑的偏差和干扰因素较多，界面直观易用。平台能够帮助科研人员对多偏差条件下分离过程分离体的运动范围、潜在风险以及失败概率进行预测，并且辅助科研人员进行分离机构的设计开发和验证，模拟多种情况下分离过程，研究导致分离出现问题的原因，找到分离失败的可能情况。

［1］Singaravelu J，Jeyakumar D，Nageswara R B.Taguchi's approach for reliability and safety assessments in the stage separation process of a multistage launch vehicle［J］.Reliability Engineering&System Safety，2009，94（10）：1526-1541.

［2］Duprey K E，Saucier E R.Separation systems comparison for ares I launch Vehicle［C］∥Proc.of the 44th AIAA／ASME／SAE／ASEE Joint Propulsion Conference and Exhibit，2008：1-6.

［3］Zhu X，Li H，Yu T，et al.Research on reliability analysis for low-altitude and high-speed payload fairing separation［C］∥Proc.of the International Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering，2013：90-94.

［4］Singaravelu J，Jeyakumar D，Nageswara R B.Reliability and safety assessments of the satellite separation process of a typical launch vehicle［J］.The Journal of Defense Modeling and Simulation：Applications，Methodology，Technology，2012，9（4）：369-382.

［5］Oh C S，Sun B C，Park Y K，et al.Payload fairing separation analysis using constraint force equation［C］∥Proc.of the Inter-national Conference on Control，Automation and Systems，2010：1134-1138.

［6］Roshanian J，Talebi M.Monte Carlo simulation of stage separation dynamics of a multistage launch vehicle［J］.Applied Mathematics and Mechanics，2008，29（11）：1411-1426.

［7］Pamadi B N，Tartabini P V，Toniolo M D，et al.Application of constraint force equation methodology for launch vehicle stage separation［J］.Journal of Spacecraft and Rockets，2013，50（1）：191-205.

［8］Gusman M R，Barad M F.Aerodynamic database generation for SRB separation from a heavy lift launch vehicle［C］∥Proc.of the 29th AIAA Applied Aerodynamics Conference，2011：1-10.

［9］Jia R Y，Jiang Z Y，Zhang W H.Simulation of off-nominal parameters disturbance of hypersonic vehicle stage separation［J］.Journal of Rocket Technology，2012，35（5）：578-582.（贾如岩，江振宇，张为华.高超声速飞行器级间分离偏差干扰仿真［J］.固体火箭技术，2012，35（5）：578-582.）

［10］Luo Q，Zhang W，Li W.Simulation research of a miniature missile with Monte-Carlo method［J］.Flight Dynamics，2013，1（3）：265-268.（罗俏，张伟，李伟.微型导弹蒙特卡罗打靶仿真研究［J］.飞行力学，2013，1（3）：265-268.）

［11］Schneider S A，Chen V W，Pardo-Castellote G，et al.Control-Shell：a software architecture for complex electromechanical systems［J］.The International Journal of Robotics Research，1998，17（4）：360-380.

［12］Liu X T，Liu L，Song K，Important considerations of building pattern to complicated system［J］.Journal of System Simulation，2007，19（13）：3073-3075.（刘兴堂，刘力，宋坤，等.对复杂系统建模与仿真的几点重要思考［J］.系统仿真学报，2007，19（13）：3073-3075.）

［13］Maier M W.System and software architecture reconciliation［J］.

Systems Engineering，2006，9（2）：146-159.

［14］Garcia J G，Ortega JG，Garcia A S，et al.Robotic software architecture for multisensor fusion system［J］.IEEE Trans.on Industrial Electronics，2009，56（3）：766-777.

［15］Wu X G，Yang Y J.The design of integrated simulation for underwater weapon system［J］.Systems Engineering and Electronics，1996，18（7）：61-68.（吴旭光，杨益军.水下武器系统一体化仿真技术研究与设计［J］.系统工程与电子技术，1996，18（7）：61-68.）

［16］Bunzel S.AUTOSAR-the standardized software architecture［J］.Informatik-Spektrum，2011，34（1）：79-83.

［17］Miyachi C.Agile software architecture［J］.Association for Computing Machinery（ACM）Special Interest Group on Software Engineering（SIGSOFT）Software Engineering Notes，2011，36（2）：1-3.

［18］LüM L.Research on the rocket flight process simulation based on multi-body dynamic method［D］.Beijing：Beijing Jiaotong University，2013.（吕明亮.基于多体动力学的火箭飞行仿真研究［D］.北京：北京交通大学，2013.）

［19］Wang F.The load calculation of launch vehicle and common software implementation［D］.Changsha：National University of Defense Technology，2001.（王锋.运载火箭载荷计算及通用软件实现［D］.长沙：国防科学技术大学，2001.）

［20］Zheng L，Song Z Y.Algorithms to generate pseudo random numbers and comparison［J］.Journal of Hubei University of Technology，2008，23（5）：65-68.（郑列，宋正义.伪随机数生成算法及比较［J］.湖北工业大学学报，2008，23（5）：65-68.）

Design of separation process Monte-Carlo simulation platform considering multiple factors

LI Hui-tong，ZHAO Yang
（School of Astronautics，Harbin Institute of Technology，Harbin 150001，China）

Launch vehicles such as rocket and missile always experience a variety of separations in flights，and any problem in the process of separations may result in failure of the whole task.The separation process of detached body is influenced by many kinds of interferences and errors，and the trial number of target range is generally limited，thus it is difficult to precisely determine the influence of multiple factors in the separation process.A general separation model is designed，and a separation load library containing many forces and interferences is established.The simulation platform is on the base of Monte-Carlo method which can be used into simulation analysis for many different kinds of separation process，and then obtain the outcome considering the influence of multiple factors.The Monte-Carlo trajectory simulation for separation process of some missile hood is carried out and the detached body movement range is acquired.

simulation；Monte-Carlo method；separation of missile hood

V 475 文献标志码：A DOI：10.3969／j.issn.1001-506X.2015.09.32

李慧通（1988-），男，博士研究生，主要研究方向为飞行器仿真、多体动力学。

E-mail：lihuitongyx＠126.com

赵 阳（1968 ），男，教授，博士，博士研究生导师，主要研究方向为飞行器仿真、振动与冲击。

E-mail：yangzhao＠hit.edu.cn

1001-506X（2015）09-2169-07

2014-08-18；

2015-01-04；网络优先出版日期：2015-03-23。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150323.1706.003.html