基于改进遗传算法的混装线多目标优化

韩煜东，董双飞，谭柏川

（重庆交通大学 管理学院，重庆 400074）

0 引言

近年来，由于消费者越来越追求产品的个性化、多样化、定制化，单一型号的产品装配线已无法满足消费者的需求，因此可以装配多种型号产品的混流装配线应运而生。混流装配线已广泛应用于汽车、电子、家电、服装等产业中［1］。为提高生产效率、降低瓶颈工位对生产速度的制约，在生产线设计阶段，需要在满足产品装配工艺先后顺序、市场需求量及其他约束的情况下，设计合理的生产节拍，将各任务分配到各工作站，使各工作站负荷均衡，即：装配线平衡设计问题［2］。

由于装配线平衡问题属于组合优化问题，是典型的NP－Hard问题。而且混流装配线上产品的需求速率不断变化，譬如家电类产品当季节性需求变化、某类产品的剧增以及新产品引入生产线时，极易造成生产线的混乱，使得人员的配置以及加工时间随之发生变化，此时对混流装配线的平衡就必须兼顾多方面。应用多目标优化可以有效协调生产线上工作站数量、生产节拍、工作站负荷以及工人加工成本之间的关系，但是针对这类问题还没有一种精确的方法进行求解。目前解决装配线平衡问题的方法主要是数学规划方法和启发式算法。Ana Sofia Simaria在工人人数确定的前提下，提出了优化生产节拍与工作站均衡的模型，并将两个不同的模型综合为一个模型，利用遗传算法对模型进行求解［3］；Talbot等利用启发式算法求解装配线平衡问题［4］；Lapierre等采用禁忌搜索算法对装配线平衡问题进行求解［5］；Manavizadeh等在定制与随机的环境下，提出了优化工作节拍和工作站的模型，采用多目标遗传算法求解与多目标进化算法验证并寻找最优方法的方式进行研究［6］；Betul提出了工作站数量的变化导致加工时间的变化，针对生产能力效率、各工作站时间的均衡以及生产线平滑问题，采用蚁群算法对其进行求解［7］。通过以上分析可知，已有文献主要集中研究工作站或生产节拍的单目标，对工作站或生产节拍的制约因素考虑得较少，而且由于约束条件存在量级差异性，在多目标转化的综合模型中权重系数的确定主观性较强。

苑明海等在大规模定制的前提下，针对混流装配线平衡问题建立了工作站数量、工作站负荷以及装配线效率的数学模型，并采用模拟退火算法与遗传算法相结合的方式进行了平衡计算［8］；公绪霞等采用模糊优化理论，建立了装配线平衡问题的多目标非线性规划模型［9］；李明等应用多层规划对建立的混流装配线最大工位持续时间最小和总作业时间最短的多目标模型进行平衡调度方案的研究［10］；于兆勤等从兼顾混流装配线平均负荷和瞬时负荷出发，提出综合运用遗传算法和仿真分析对平衡问题进行求解［11］；彭慧等从混流装配线的瞬时负荷平衡和生产节拍两方面研究混流装配线平衡问题，设置系数将两个目标转化为单目标，采用迭代遗传算法对目标进行求解［12］；杨才君等针对混流装配线的再平衡问题提出新平衡工作站数、不同工作站生产不同型号产品的负荷波动和调整成本模型，利用多目标遗传算法对建立的模型进行求解［13］。通过以上分析可知，已有文献主要集中在混流装配线模型的建立，而混流装配线上人员以及时间的多变性增加了平衡的难度，显然现有的优化目标以及求解方式较难满足当前汽车、电子等行业的要求。

本文根据上述分析，针对模型建立、求解方式等问题展开研究，以混流装配线实际生产节拍时间最小化和分配合适的工人到相应的工作站以降低产品的加工成本为目标，建立混流装配线平衡模型。考虑到求解的复杂性，改进交叉与变异操作，提出种群扩张机制，设计基于自然数序列的遗传算法对本文建立的数学模型进行求解。最后，结合实际算例对模型和算法进行有效性检验与分析。

1 模型建立

1.1 问题描述

混流装配线即使在同一平台上生产p种产品，每种产品的工艺要求都不尽相同，使得不同产品的作业元素及作业顺序有一定差异。为研究p种不同型号产品的混流装配线平衡问题，首先将每种产品的作业顺序图合成为一个综合作业顺序图。如图1～图4所示。综合作业顺序图包含了p种产品的n个作业任务，对于同一作业元素，不同产品的作业时间可能不同，当一种产品的装配不包含其中某项作业元素时，该作业元素的作业时间为零。本文在建立不同产品需求速率（企业已有的工作站数不能改变）的前提下，通过调节生产节拍以及降低产品的加工成本来实现混流装配线的平衡。

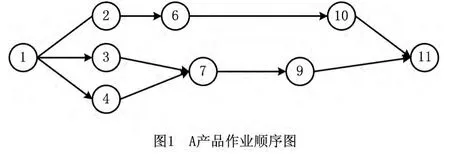
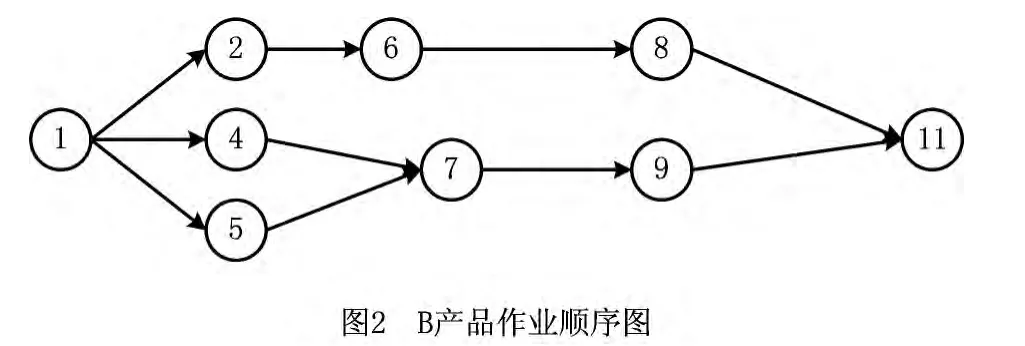
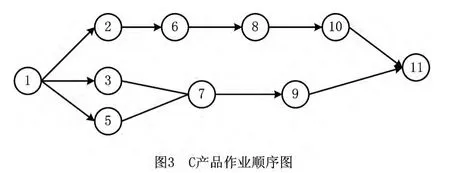
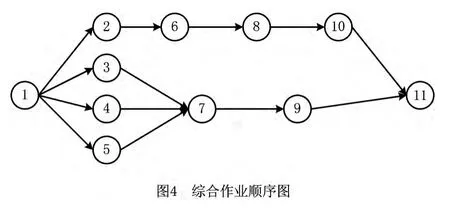
该问题的基本假定如下：

（1）不同产品的相同任务分配到同一个工作站；

（2）任务之间的先后顺序已知，不同产品的任务先后顺序图可以综合为一个先后顺序图；

（3）任务时间确定，不同产品的相同任务的操作时间可能不同；

（4）每个工作站内的任务加权时间不超过节拍时间，无并行工作站；

（5）每个工作站只有一个人。

1.2 多目标优化的数学模型

该问题的参数和决策变量采用如下符号：

（1）参数

n为任务总数；

p为产品型号数；

ciω为工人ω操作任务i的操作成本；

dj为产品j的需求量；

k为工作站数，k＝1，2，…，n；

wj为产品型号j在总产量中的比重，j＝1，2，…，p；

tij为产品j的任务i的作业时间，i＝1，2，…，n，j＝1，2，…，p；

pre（i）为按照任务的先后顺序，先于任务i完成的任务集合，i＝1，2，…，n。

（2）决策变量

在装配线生产中，由于工人的文化程度和工作经验不同，导致操作相同任务所花费的时间不同，在此期间发生的费用具有一定的差异性。因此安排合适的工人去对应的工作站以降低产品的总加工成本，在混流装配线平衡中就显得很有实际价值。表1所示为四个工人操作相同任务所产生的费用。

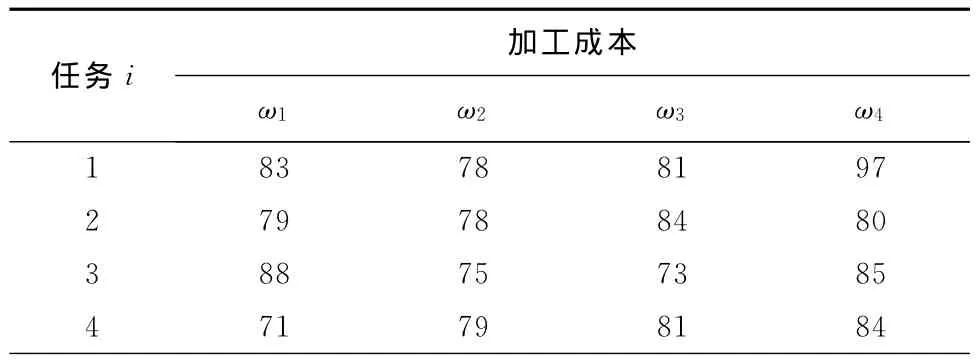
表1 不同工人加工产品所需成本

续表1

安排合适的工人到相应的工作站，使得产品的加工成本最小。如果工人ω，任务i被分配到工作站k，则工作站k内产品的加工成本为：

混流装配线加工产品所产生的总成本为：

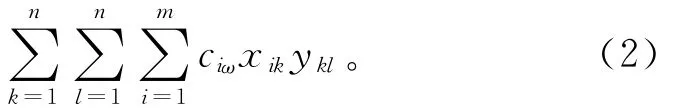
因此，混流装配线多目标平衡优化模型可以表示为：

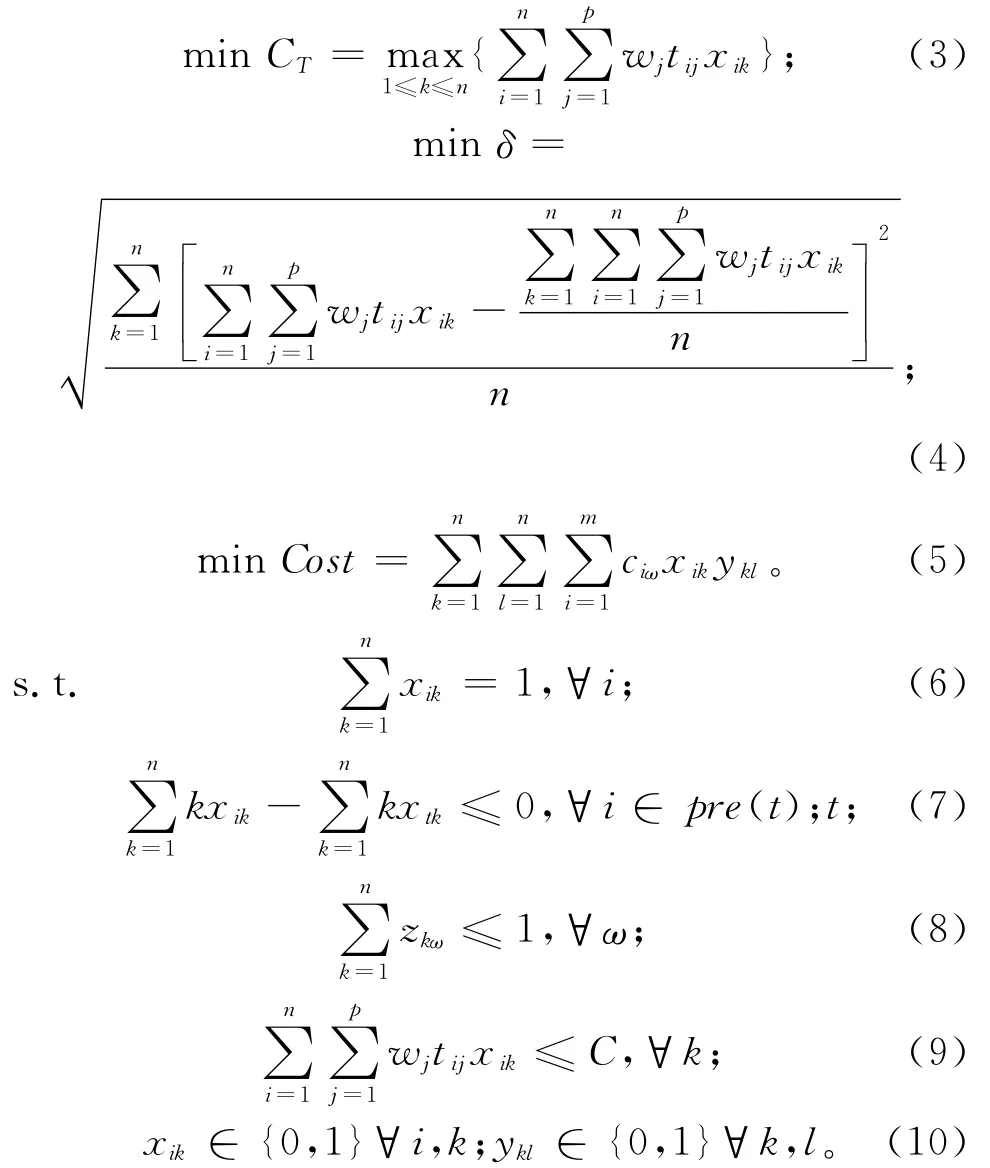
其中：第一个目标函数（3）是使各工作站所有产品的加权任务总时间的最大值最小化，即优化装配线的生产节拍；第二个目标函数（4）使各工作站时间的均方差最小化，即均衡各工作站的加权任务时间；第三个目标函数（5）是使得产品的加工成本最小；约束（6）表示每个任务都被分配但只能分配到一个工作站；约束（7）表示必须遵守任务的优先顺序关系；约束（8）表示每个工人最多只能分配到一个工作站；约束（9）表示节拍时间约束，即分配到每个工作站的所有产品的加权任务总时间不得超过事先规定的节拍时间；约束（10）表示任务分配和工人分配的决策变量都是0/1型变量。

2 针对混流装配线多目标平衡优化设计遗传算法

对于多目标平衡问题，一般通过将多目标问题转化为单目标问题以降低问题的复杂性的方式，赋予每个目标权重或者目标规划进行求解。然而对单一目标的混流装配线进行优化，往往由于实际规模的数据量较大，导致混流装配线问题难以采用精确的算法求解。

遗传算法是一种自适应的随机化搜索方法，具有良好的稳定性、内在的隐并性和全局寻优能力，直接对结构对象进行操作且不要求优化函数连续或可导，已被广泛应用于处理多目标优化问题以及装配线平衡问题。本文针对提出的优化目标，设计了一种改进的遗传算法来处理混流装配线平衡问题。通过对编码方式的优化，增加了算法的可视化操作；利用拓扑排序理论生成初始种群，生成的个体为可行解，增强了算法的可靠性并提高了其寻优速度；选择适应度值高的个体进入配对池；设计交叉、变异算子，用于前期扩大搜索范围、后期保护优秀个体；提出种群扩张机制以提高算法的全局寻优能力。

2.1 编码与插零操作

采用基于作业顺序的染色体编码规则，按照作业的先后顺序，将n个作业元素排成一排，每个作业元素对应一个基因位，作业元素按作业顺序分配到各个工作站，工作站中产品的加权时间不能超过预先设定的生产节拍，按照工作站中工序的排列顺序进行编码。最终该染色体是采用由n个作业元素和k＋1个零组成的长度为n＋k＋1的编码方式，其中零可表示当前工作站的作业元素开始（或结束）位置，两个零之间的作业元素表示同属于一个工作站，如图5所示。

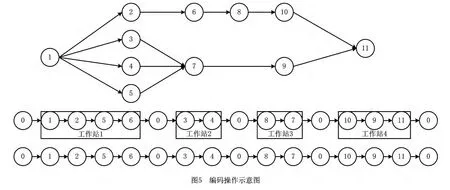
2.2 生成初始种群

初始种群的好坏将直接决定进化过程的优劣，好的初始种群将提高算法的运行效率。为保证初始种群中个体的多样性与解的可行性，采用拓扑排序和随机搜索法来生成初始种群，过程如下：

步骤1 令混流装配线的任务合集TS＝｛ts1，ts2，…，tsn｝。

步骤2 根据综合作业顺序图，从集合TS中找出无紧前或者是紧前已分配的任务放入集合TS1中，并在综合作业图中删除选出的任务i和与之有关的逻辑顺序。

步骤3 从集合TS1中随机选择一个任务，放入相应的基因位置。

步骤4 如果任务集合TS＝Ø，则分配结束，否则转步骤2。

在初始种群的生成过程中，每次分配任务都保证其紧前任务均被分配，从而保证了种群中个体的可行性，采用拓扑排序与随机搜索相结合的方式，保证了初始种群具有足够的多样性。

2.3 解码

针对设定的工作站数量，对初始种群的每一个可行解，按照计算的最小节拍Ctheory划分到不同的工作站中，从而判断初始种群中个体的优劣。

步骤1 初始化节拍：计算理论最小节拍Ctheory＝Total/k，Total为所有作业元素加工不同产品的加权总作业时间，k为给定的工作站数，令C＊＝Ctheory。

步骤2 以C＊为节拍，按照作业元素的分配顺序，n个作业元素分配至k个工作站中，每个工作站的时间分别为T1，T2，…，Tk，k＝1，2，…，n。如果每个工作站的时间Tk≤C＊，则C＊就是这种排列下的最小节拍，搜索停止；否则执行步骤3。

步骤3 计算装配线节拍的潜在增量Δ1，Δ2，…，Δn－1，其中Δk，k＝1，2，…，（n－1）的值分别是第k＋1个工作站的第一个作业元素的时间。

通过每个个体的解码操作，确定种群中个体工作站任务的分配，此时在每个工作站之间进行插零操作，以提高算法的可视化操作。

2.4 适应度

由于本文建立数学模型的目标函数为求最小值，个体的适应度值与种群中个体的目标函数值相悖，即个体目标函数值越小，其对应的适应度值越大。因此其适应度函数可以设计如下：

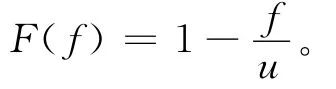
式中：f为个体对应的目标函数；u为不小于maxf的常数。为保证遗传算法在进化初期保持种群的多样性，在进化后期突出优良个体，本文应用适应度尺度变换法，缩小进化初期个体适应度的差异，扩大进化后期个体适应度的差异［11］。

2.5 选择

步骤1 计算出整个种群的适应度值的总和S。

步骤2 将每个个体的适应度值以随机的顺序映射到实线段［0，S］上相对应的线段上，从而每一线段的长度就与相对应的适应度值的大小成比例，如图6所示。

步骤3 从间隔［0，S/N］中随机选取一个数S0，S/N为适应度值的平均值。

步骤4 计算出N个平均分布的数Si，其中Si＝S0＋i×（S/N），i＝0，1，2，…，N－1。计算集合｛Si｝中落在间隔k上值的个数，记为nk，如图7所示。

步骤5 对于每一个k（k＝1，2，…，N），将个体k复制nk次。这种选择方法保证了适应度值高于群体平均适应度值的个体一定会被选择，从而加快算法的收敛速度。

2.6 交叉与变异

2.6.1 交叉操作

针对问题的特性和编码方式，本文采用两点交叉方法。从种群中随机选取两个染色体作为父代1、父代2并随意生成两个交叉点γ1、γ2（1≤γ1＜γ2≤n），将两个父代染色体分为前中后三部分。取出父代1中染色体的中间部分，同时在父代2中查找这部分基因的排列顺序，用父代2中的排列顺序取代原来的排列顺序，生成子代1；同理，取出父代2中染色体的中间部分，同时在父代1中查找这部分基因的排列顺序，用父代1中的排列顺序取代原来的排列顺序，生成子代2。

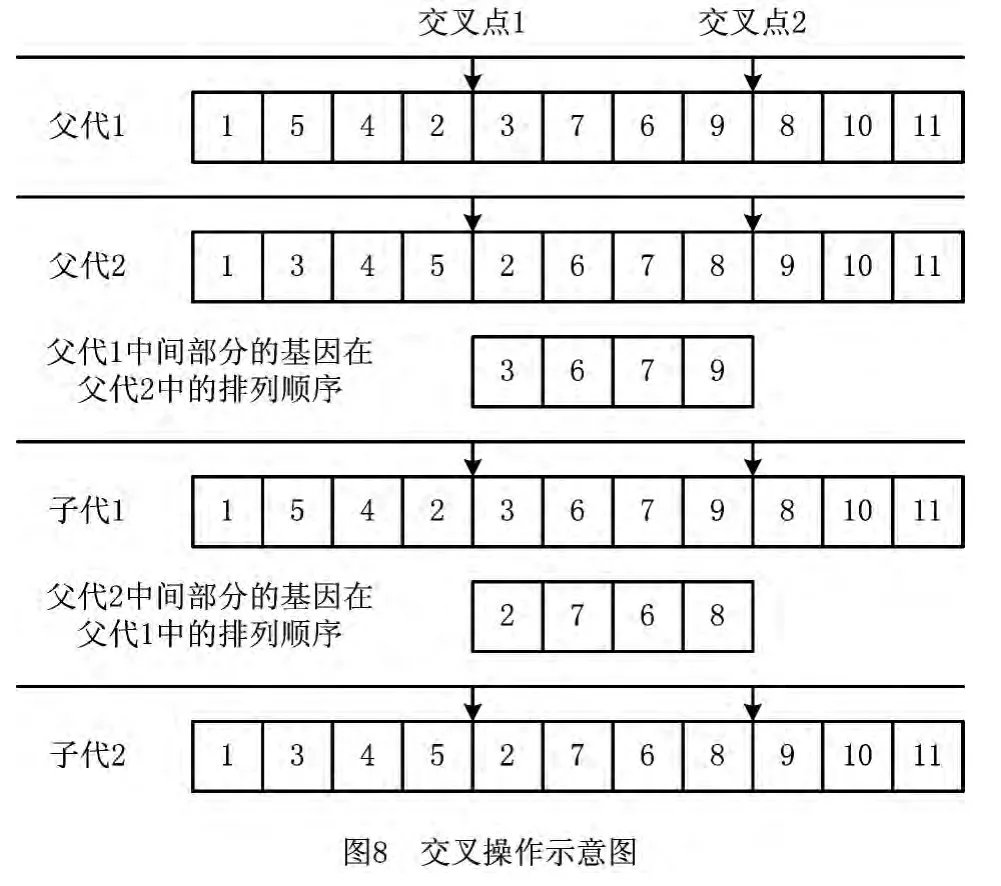
2.6.2 变异操作

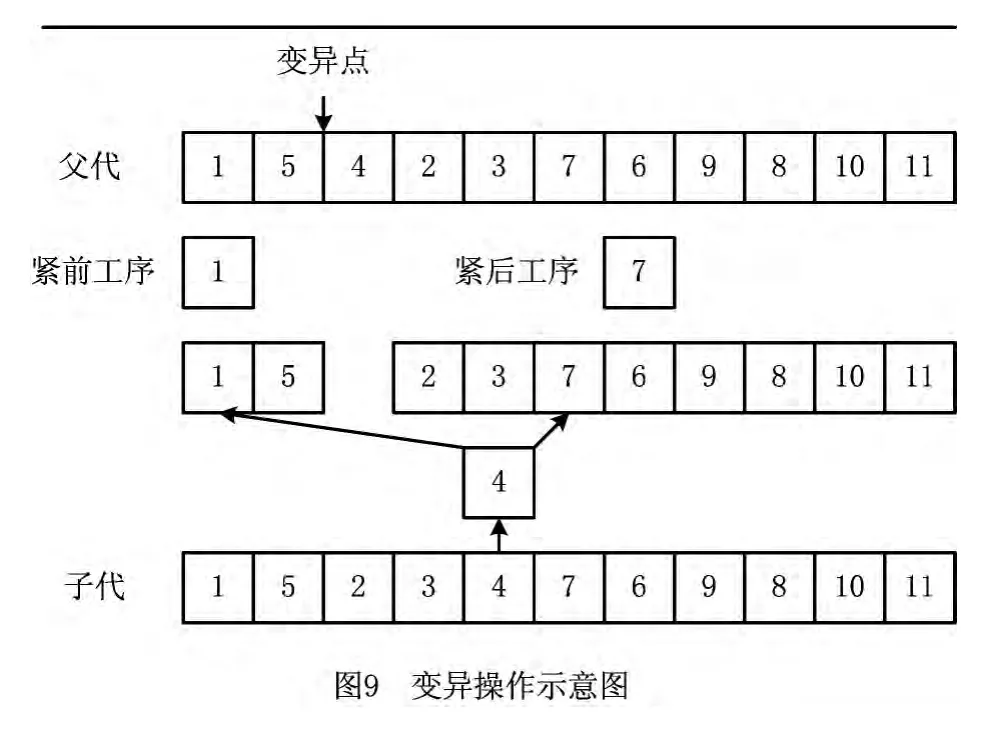
随机产生一个染色体作为父代，然后产生一个变异点1≤γ3≤n。找出变异点的紧前工序与紧后工序，保持紧前工序及其以前的基因位置不变，保持紧后工序及其之后的基因位置不变，将变异点随机插入染色体中紧前工序与紧后工序之间的基因位置，将这三部分基因合成为一个就生成了子代染色体（如图9）。

2.6.3 算子设计

初始种群的个体虽然是可行解，但在算法运行的早期，无法判断出最优个体是否出现。因此可以增大交叉和变异的概率以增强算法的寻优能力；在迭代后期，算法逐渐收敛时，个体适应度值变高，为不破坏个体中基因的优良性，此时往往减小交叉和变异的概率，以提高算法的运行效率，

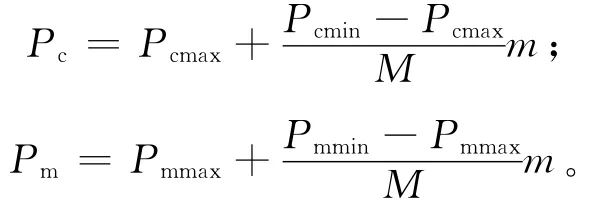
式中：M为最大迭代次数，m为迭代次数，Pc为交叉概率，Pm为变异概率，Pcmin为最小交叉概率，Pcmax为最大交叉概率，Pmmin为最小变异概率，Pmmax为最大变异概率。

由于装配线的优化涉及任务之间的逻辑关系，本文算法的迭代步骤都受到约束关系的制约，从而保证在算法运行中的所有个体都为可行解，以此加快算法的寻优速度；此外，提出的改进遗传算法通过增设种群扩张机制提高了算法的全局寻优能力，按种群中个体适应度值的大小排序，将子代种群中R个个体和父代种群中适应度值小的前r个个体共同构成一个包含（R＋r）个个体的新种群，对新种群个体进行交叉和变异操作，产生R个新的子代种群个体，扩大种群的搜索范围。

综上所述，本文设计的遗传算法思路如图10所示。

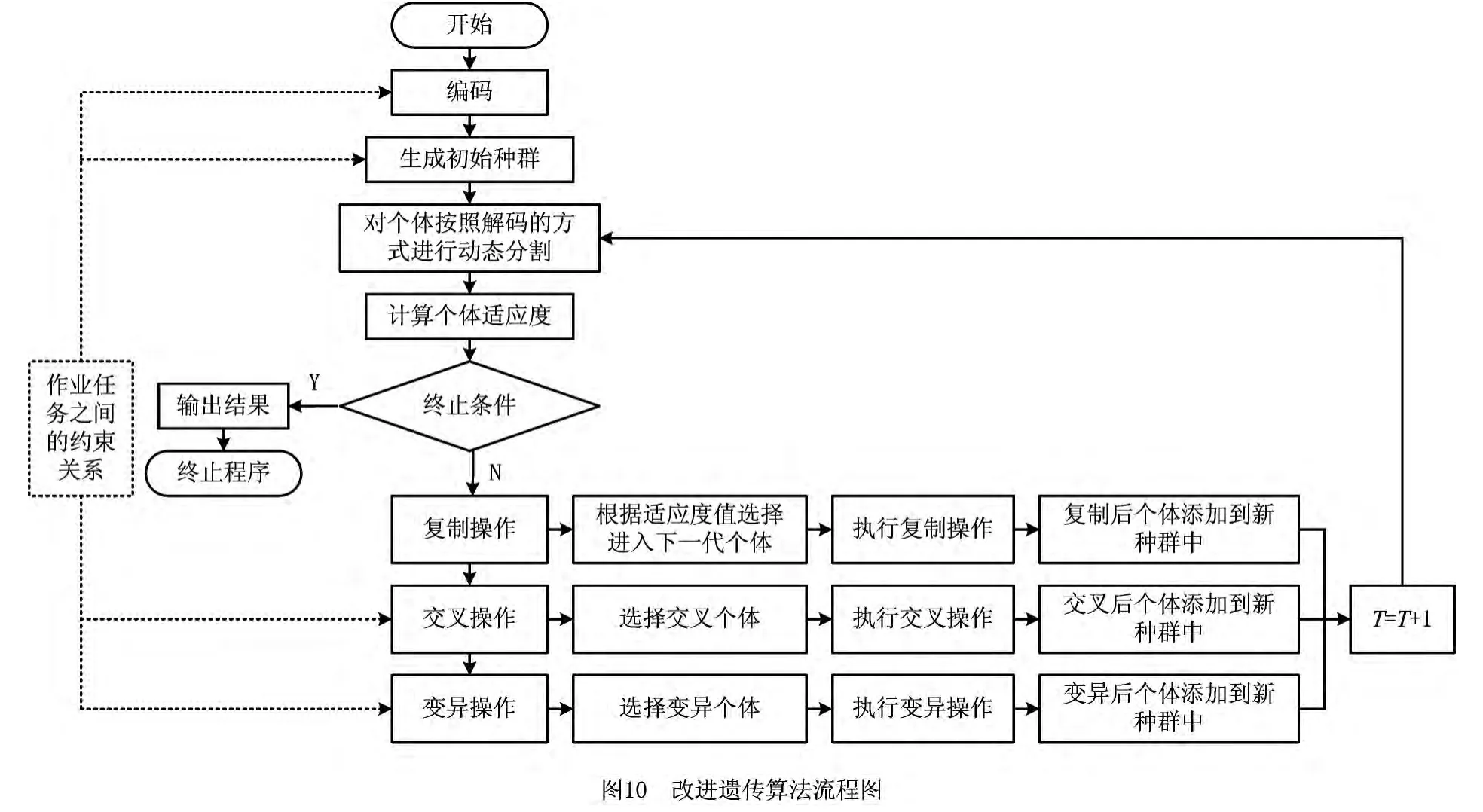
3 数值试验

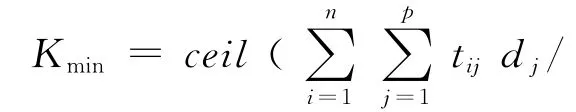
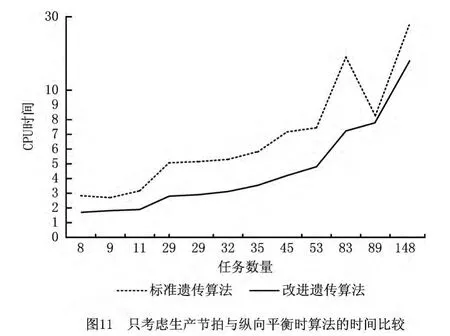
为了便于与标准遗传算法进行对比，首先，只考虑最小生产节拍与纵向平衡两个目标。采用本文提出的改进遗传算法和标准遗传算法进行求解，对比结果如表2所示。从表中可以看出，所有案例的测试结果都表明改进的遗传算法在处理混流装配线平衡问题上优于标准遗传算法。在运行时间上，改进遗传算法具有一定的优势（如图11）。

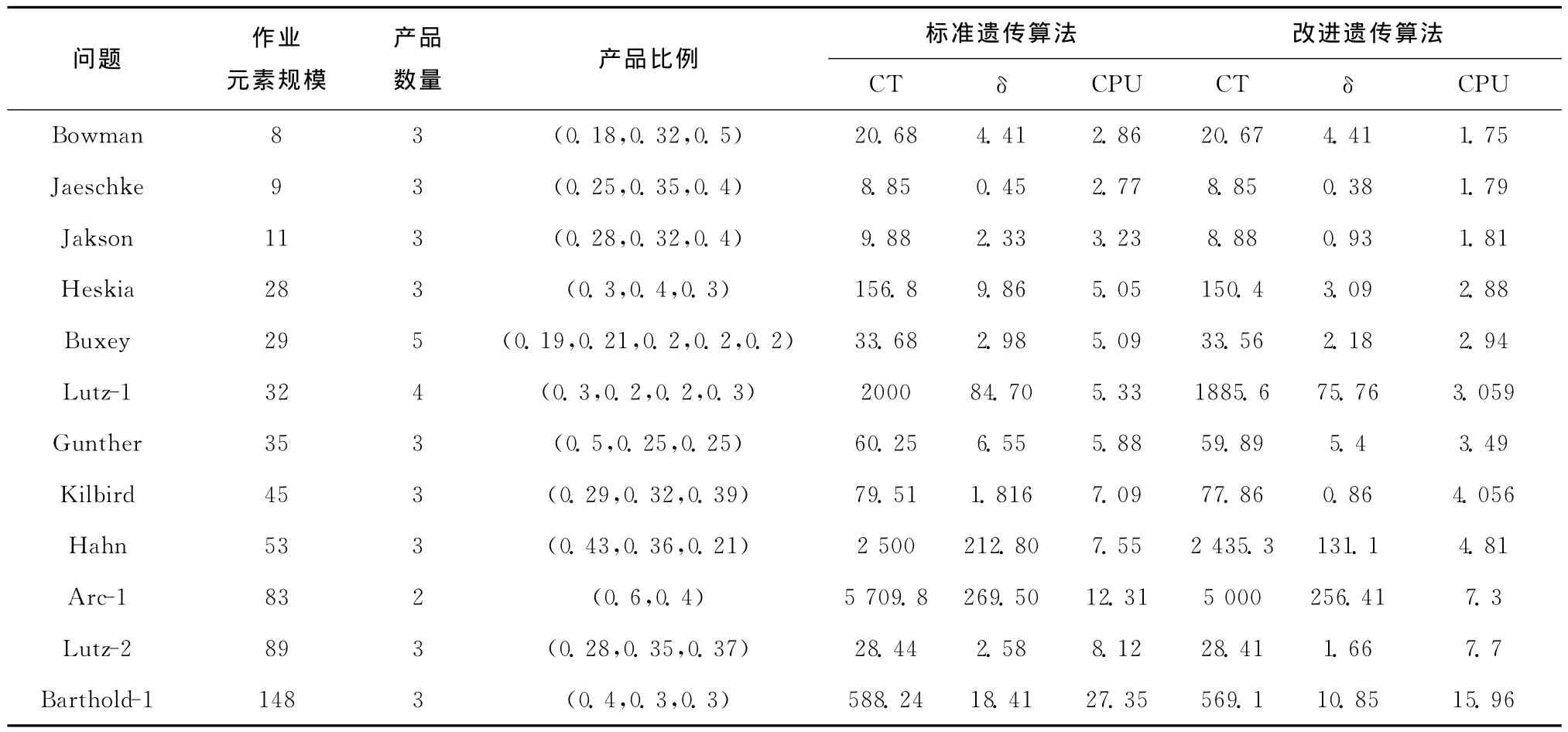
表2 优化生产节拍与纵向平衡的结果对比

然后，同时考虑最小化生产节拍、各工作站内产品加权任务时间均衡、安排相应工人进入对应工作站以降低产品加工成本三个目标，采用改进遗传算法求解。表3所示为求解结果。

最后，为了验证改进遗传算法的有效性，采用文献［11］的数据进行分析。该问题包含3种产品和39个任务，任务之间的综合顺序关系如图12所示，每种产品的作业时间以及不同工人加工不同产品的成本如表4和表5所示。通过计算，表6给出了该问题的文献中的算法、标准遗传算法和改进遗传算法求解的最终优化结果。

表3 同时考虑三个目标的测试结果

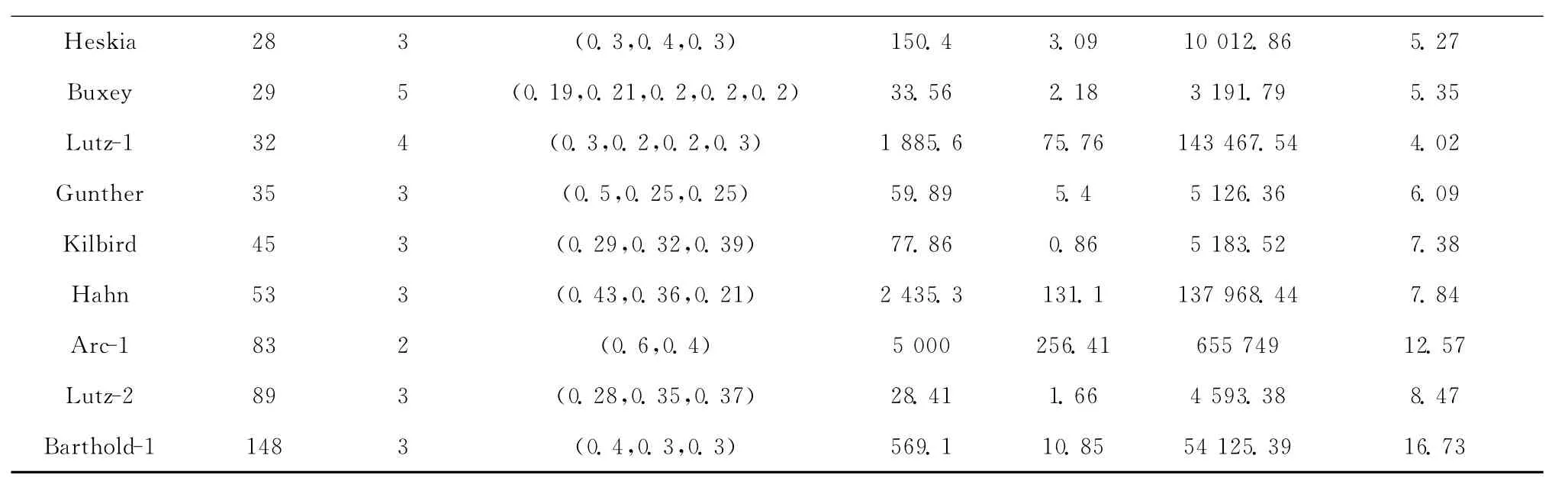
续表3

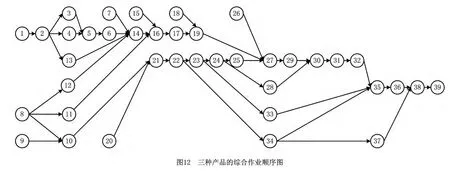
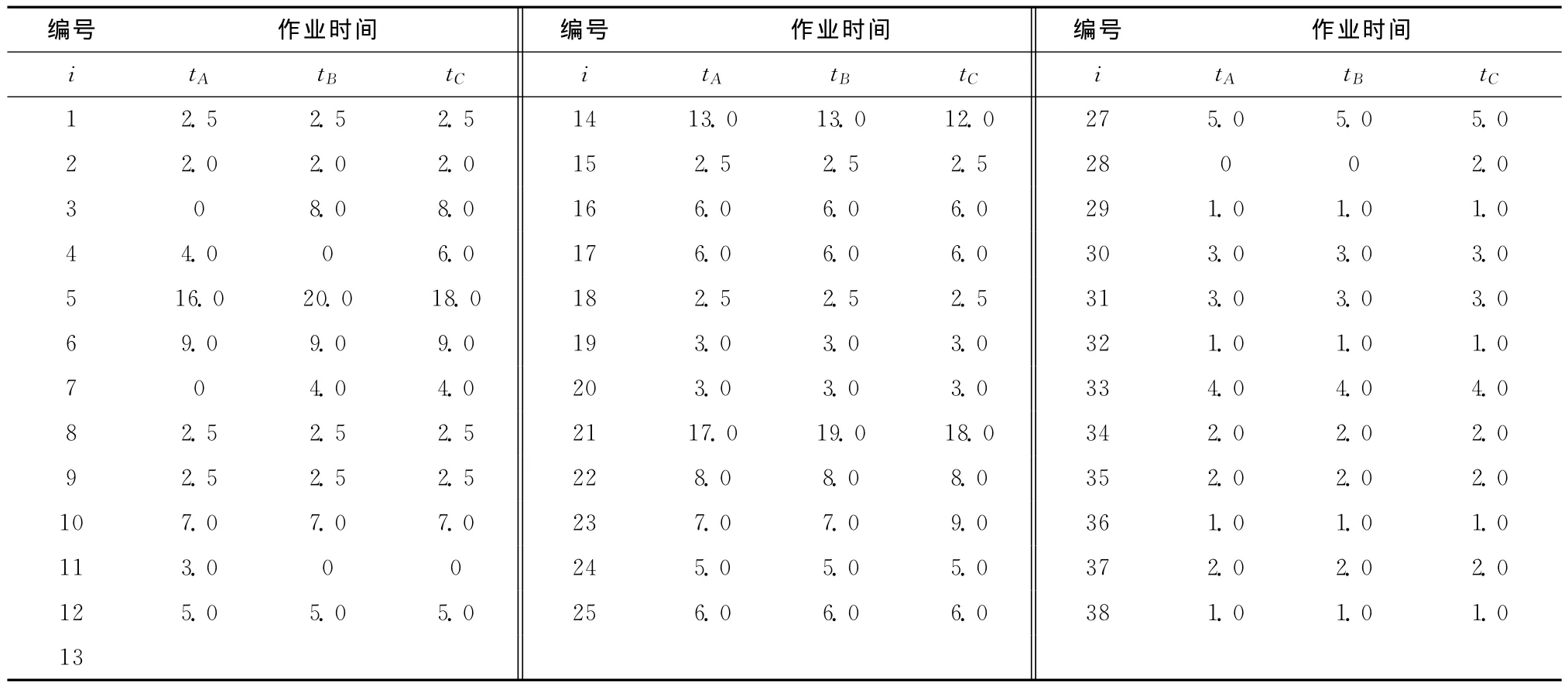
表4 每个任务的作业时间

表5 每个工人的加工成本

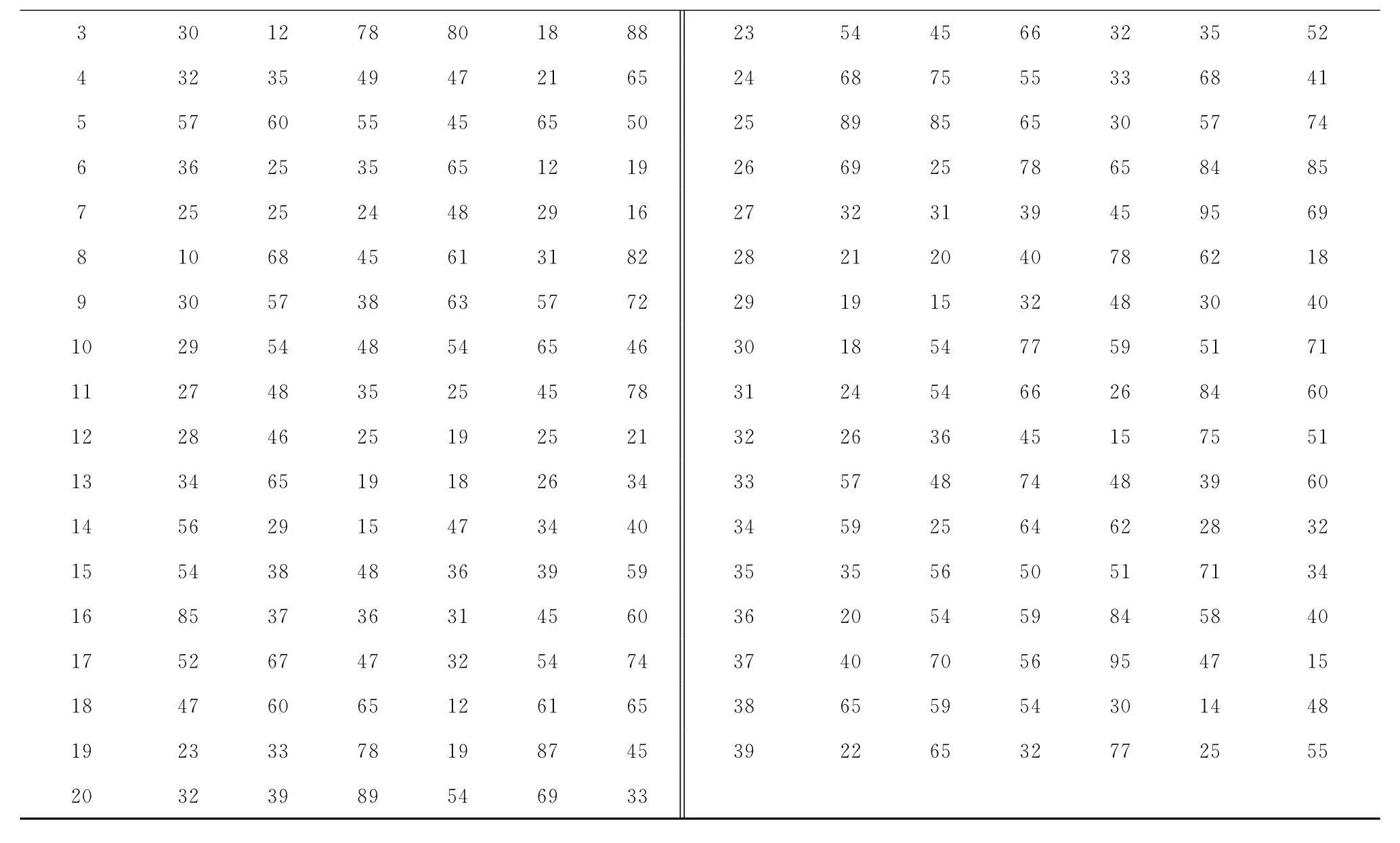
续表5

表6 优化结果

4 结束语

混流装配线平衡对越来越重视生产线效率以及质量的汽车、电子等制造型企业具有十分重要的现实意义。本文对混流装配线平衡问题建立了多目标模型并进行了优化研究，从优化生产节拍、保证各工作站的加工时间均衡以及优化产品的加工成本方面建立了相应的数学模型，针对建立的模型，运用自然数序列编码策略和拓扑排序理论，改进算法的交叉、变异操作并进行求解。通过实例验算表明了本文提出的改进遗传算法能够有效解决混流装配线多目标问题。针对具体企业的产品需求速率变化，通过应用该算法改进了混流装配线的生产效率，提升了企业的产能，使企业能更好地满足消费者的需求。本文所设计的改进遗传算法还可以进一步用于双边、U型混流装配线多目标平衡优化的研究。

［1］ LI Bin，CHEN Liping，HUANG Zhengdong，et al.Research on assembly line optimal scheduling for mass customization production［J］.China Mechanical Engineering，2005，16（24）：2198－2201（in Chinese）.［李 斌，陈立平，黄正东，等.面向大规模定制的装配线优化调度研究［J］.中国机械工程，2005，16（24）：2198－2201.］

［2］ BOYSEN N，FLIENDER M，SCHOLL A.A classification of assembly line balancing problem［J］.European Journal of Operational Research，2007，183（2）：674－693.

［3］ SIMARIA A S，VILARINHO P M.A genetic algorithm based approach to the mixed－model assembly line balancing problem of typeⅡ［J］.Computers ＆Industrial Engineering，2004，47（4）：391－407.

［4］ TALBOST F B，PATTERSON J H，GEHRLEIN W V.A comparative evaluation of heuristic line balancing techniques［J］.Management Science，1986，32（4）：430－454.

［5］ LAPIERRE S D，RUIZ A，SORIANO P.Balancing assembly lines with tabu search［J］.European Journal of Operational Research，2006，168（3）：826－837.

［6］ MANAVIZADEB N，PABBANI M，MOSHTAGHI D，et al.Mixed－model assembly line balancing in the make－to－order and stochastic environment using multi－objective evolutionary algorithms［J］.Expert Systems with Applications，2012，39（15）：12026－12031.

［7］ YAGMAHAN B.Mixed－model assembly line balancing using a multi－objective ant colony optimization approach［J］.Expert Systems with Applications，2011，38（10）：12453－12461.

［8］ YUAN Minghai，LI Dongbo，YU Minjian.Mixed－model assembly for mass customization［J］.Computer Integrated Manufacturing Systems，2008，14（1）：79－83（in Chinese）.［苑明海，李东波，于敏建.面向大规模定制的混流装配线平衡研究［J］.计算机集成制造系统，2008，14（1）：79－83.］

［9］ GONG Xuxia，QI Ershi，LIU Liang.Multi－objective optimization for assembly line balancing problem based on fuzzy optimi－zation theory［J］.Machinery Design ＆ Manufacture，2013，7（7）：247－250（in Chinese）.［公绪霞，齐二石，刘 亮.基于模糊优化理论的装配线平衡多目标优化［J］.机械设计与制造，2013，7（7）：247－250.］

［10］ LI Ming，TANG Qiuhua，XI Zhongmin，et al.One－sided multi－objective assembly line model based on multi－layer programming［J］.Systems Engineering—Theory ＆ Practice，2011，31（11）：2185－2190（in Chinese）.［李 明，唐秋华，席忠民，等.基于多层规划的单边多目标装配线平衡调度模型［J］.系统工程理论与实践，2011，31（11）：2185－2190.］

［11］ YU Zhaoqin，SU Ping.Combining genetic algorithm and simulation analysis for mixed－model assembly line balancing problem［J］.Computer Integrated Manufacturing Systems，2008，14（6）：1120－1129（in Chinese）.［于兆勤，苏 平.基于遗传算法和仿真分析的混合装配线平衡问题研究［J］.计算机集成制造系统，2008，14（6）：1120－1129.］

［12］ PEN Hui，XU Kelin，SI Zhanhua.Multi－objective optimization for mixed－model assembly line balancing problem based on genetic algorithm［J］.Modern Manufacturing Engineering，2011，13（11）：49－53（in Chinese）.［彭 慧，徐克林，佀占华.采用遗传算法的混流装配线平衡多目标优化［J］.现代制造工程，2011，13（11）：49－53.］

［13］ YANG Caijun，GAO Jie，SUN Linyan. Multi－objective mixed－model assembly line rebalancing：model and algorithm［J］.Systems Engineering—Theory ＆ Practice，2013，33（8）：1956－1964（in Chinese）.［杨才君，高 杰，孙林岩.多目标混流装配线再平衡模型与算法［J］.系统工程理论与实践，2013，33（8）：1956－1964.］