Black-Scholes公式推导方法及其发展推广

王明辉

（韶关学院数学与统计学院，广东韶关512005）

Black-Scholes公式推导方法及其发展推广

王明辉

（韶关学院数学与统计学院，广东韶关512005）

摘要：从Black-Scholes模型的理论背景和假设条件出发，分析了该模型中期权定价公式的推导过程和国内外学者的不同推导方法，最后从放宽假设条件和扩展期权类别两个方面探讨了该公式的推广形式．

关键词：Black-Scholes模型；期权定价公式；发展推广

1973年F Black和M S Scholes从欧式看涨期权入手，运用均衡资本资产定价理论，推导出至今广为流传的欧式看涨期权定价公式［1］，即Black-Scholes期权定价公式．由于公式中所有的参数都是可估的，因此在实践中得到了广泛应用．

1　Black-Scholes模型定价公式的推导

F Black和M S Scholes从市场有效的假定出发，假设股票的价格运动过程服从马尔科夫链，只与现在的价格有关．构造一个证券投资组合，使得在此组合中能够根据标的资产价格的变化连续调整标的资产的头寸，进而使得该组合在短期内保持无风险状态，那么该组合的收益率就为无风险收益率，此时该组合的动力系统就可以由一个随机微分方程给出．一般情况下，该组合方式不唯一，因此无法很好地确定期权的价格．但如果借助套利定价理论给出与原概率测度等价的风险中立概率测度，使得折现的标的资产价格过程在这一新测度下为鞅或局部鞅，并且对套利保值投资组合的可积性给以一定的约束，使其在原始概率下平方可积，那么就存在唯一的套期保值投资组合，也就存在唯一确定的期权价格．他们还假设所有投资者都是风险中性的，投资组合只获得无风险收益，根据此概念，投资者未来的期望收益可以用无风险收益率进行贴现，从而获得未来任何现金流的现值，简化了期权的定价求解．

Black-Scholes模型的基本假设条件：

（1）股票价格的变化是连续的，并且服从一种带漂移的几何Brown运动，在数学上表现为Ito过程；

（2）市场无风险利率为已知常数，不随时间的变化而变化；

（3）股票不支付红利或者其他收益；

（4）期权是欧式期权，即只能在合约到期日才能执行期权；

（5）不产生交易费用和税金；

（6）标的物可无限细分，也可自由买卖；

（7）期权和标的物均可卖空．

Black-Scholes模型假设标的资产价格St服从如下随机微分方程：

其中dWt表示标准Brown运动，且：

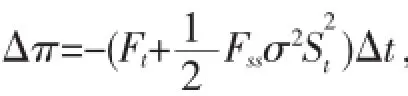
π解得：其中：

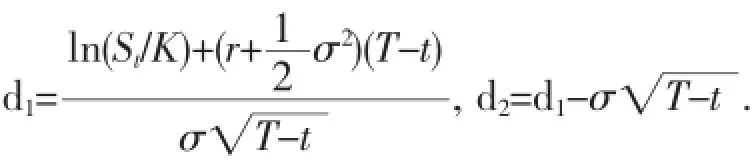
也可以写成：也就是Black-Scholes期权定价公式．

F Black和M S Schole的论文不仅在理论上有重大作用，而且在对金融市场的实际操作也有着巨大的影响，其公式在期权交易中得到了广泛应用．正是由于其巨大的应用价值，国内外众多的数学家、金融学家和计算机专家都对其进行了大量研究．

Duffie介绍了四种推导Black-Scholes公式的方法［2］：

第一，二项定价模型．首先将时间区间离散化，使得每一小段的时间区间都能够趋向于零，再假设在市场中不存在套利机会（即冗余），Black-Scholes公式便在这个概念的基础上建立起来．从一定意义上来说，当给定时间区间无限细分时，即当每一时间区间的交易数目趋向于无穷大时，离散时间交易的极限就是连续时间交易，而利用中心极限定理就可以证明Black-Scholes公式就是离散化公式的极限．

第二，连续模型．设有滤波概率空间（Ω,F,P），令W为标准Brown运动，时间集合为［0,∞），F满足期权的假设条件．给定一种股票，其价格过程S={St∶t≥0}满足随机微分方程dSt=μStdt+σStdWt（μ＞0,σ＞0），另一种为债券，其价格过程β={βt∶t≥0}满足微分方程dβt=rβtdt（0＜r＜μ），且债券有连续复利利息率r，则上式有唯一解βt=β0ert．然后利用冗余定理和Ito引理，就可将确定欧式看涨期权的市场价值转化为求解具有边界条件的偏微分方程．这里有两种方法，一是经过Fourier变换，二是利用Feynman Kac公式，便可得到Black-Scholes公式．

第四，利用Girsanov定理求解．使用一般鞅定价模型和Girsanov定理去考察Black-Scholes模型中冗余证券的估值，也可得到期权定价公式．

以上在求解Black-Scholes公式时，用到了随机过程、随机微分方程等方面的数学知识，推导过程相当繁琐，从一定程度上影响了该公式的普及和应用．国内一些学者也试图寻找简化推导的方法，如俞迎达等仅仅利用微积分和概率统计的知识就得到了对于不支付红利股票的欧式看涨期权公式，由此过程很容易就能推导出支付红利和欧式看跌期权甚至更一般的期权定价公式［3］．邓乐斌给出了两种推导该公式的方法［4］．潘冠中等在风险中性的假定下，通过对正态分布的性质和矩母函数的运用，较容易地导出了Black-Scholes公式［5］．

2　Black-Scholes模型的推广与发展

Black-Scholes期权定价模型的优点是可以得到期权定价的解析表达式，并获得清晰的定量结果，而且该解析解没有误差．该方法的缺点是只研究了欧式期权，没有给出美式期权的解析解，对于期权价格依赖于状态变量历史路径的情况难以处理，而且它的假设条件相当严格，使它过分理想化，从而与现实世界相脱离，不利于在更普遍的环境中应用，因此需要根据现实条件对其模型进行扩展．例如当股票交易中存在红利支付，或者有交易成本，或者无风险利率为随机变量，或者波动率常数弹性，或者股票价格服从指数O-U过程，或者资产收益服从分数次Brown运动时，均需对Black-Scholes模型进行适当推广，而侯迎春就主要介绍了在这六个方面对期权定价公式的扩展形式［6］．

最近几年，国内学者也对Black-Scholes模型进行了大量的研究，得到了该公式的许多扩展形式．如陈万义假定股票价格服从几何Brown运动，在一般非风险中性意义下导出了欧式看跌期权定价公式［7］，在风险中性意义下该公式就退化为一般的Black-Scholes期权定价公式．王峰等用泊松过程来描述突发信息变化对股票价格的影响，用Brown运动来描述市场连续信息对股票价格的影响，得到了由Brown运动和泊松过程共同驱动的模型［8］．苏军等对Black-Scholes模型的定价偏差进行了研究，并且假设利率是随机的，同时风险资产的价格过程服从跳一扩散过程，进而得到了该公式的改进［9］．闫海峰等在当股票价格过程遵循带有非时齐Poisson跳跃的扩散过程、广义Ornstein-Uhlenback过程模型和几何分式Brown运动过程时，采用保险精算定价的方法给出了欧式期权定价公式［10-12］．孙玉东等假定波动率是股票价格的阶可导函数，期望收益率为股票价格的连续函数，利用金融市场复制策略得到了一般的Black-Scholes偏微分方程，进而导出了定价公式［13］．FAN Kun考虑了两因素作用下马尔可夫调制随机波动率模型，一个是随机波动率因素服从均值回归的平方根过程，另一个是随机波动率因素被连续时间有限状态马尔可夫链所调制，在风险中性测度下，通过逆傅里叶变换得到了欧式期权定价公式［14］．任智格在无风险利率是变化的假定下，运用Ito公式和指数函数得到了改进的期权定价公式［15］．

上述学者均是在放宽期权假设条件的基础上对Black-Scholes定价公式进行了推广，但是世界上并不是只有欧式期权，所以国内的学者也将眼光投向了其他各种期权类型．如薛红等先假定股票价格遵循由分数Brown运动驱动的随机微分方程，得到了欧式最值期权定价公式，又研究了分数跳—扩散过程下几何平均亚式期权定价问题，获得了该条件下的看涨、看跌公式［16-17］．李志广等利用有限体积元方法，在假定波动率和期望收益率都是股票价格的一般函数的条件下，得到了美式期权定价公式，并且给出了该方法的误差估计［18］．顾锋娟等在连续支付美式分期付款期权定价模型中，构造了基于自适应网格的有限差分策略，采用中心差分格式，构造出分片一致网格，再利用光滑化技巧来处理，最后通过数值解法求得美式分期付款期权的最优执行边界和最优终止边界［19］．彭斌等在股票价格变化过程服从跳-分形Brown运动的假设下，研究了支付红利的美式看涨期权定价问题［20］．王伟等假定风险资产价格满足马尔可夫调制的跳扩散过程，利用测度变换和无套利原理给出了该模型下远期生效看涨期权的定价公式［21］．SU Xiao-nan等假定标的资产价格过程服从马尔科夫调节的几何Brown运动，特别是当市场利率、标的风险资产的预期收益率与波动率随着马尔科夫链的状态转移时，利用regime switching Esscher变换得到一个等价鞅测度，进而得到欧式幂型看涨期权的公式［22］．王嘉展等假设标的资产价格服从分数Brown运动，并且在利率为Ho-Lee的模型下，得到了随机利率下的幂期权定价公式［23］．袁国军等考虑了标的股票的价格服从跳－扩散过程的亚式期权定价问题，运用无套利原理、广义Ito公式和近似对冲跳跃风险的方法，建立了该过程中的算术平均亚式期权模型，最后给出了基于半离散化的差分求解方法，并且分析了差分格式的稳定性和误差［24］．唐玲等在股票价格波动率服从对数正态分布的假定下，利用等价鞅测度变换，得到了基于最小等价鞅测度下的，同时执行价格固定的，几何平均亚式期权定价公式，并讨论了如何求其近似解［25］．

3　　结语

本文在Black-Scholes模型的理论背景和假设条件下，给出了期权定价公式，并简要介绍了国内外学者的不同推导方法，然后讨论了该模型在不同假设条件下以及不同期权模型中的扩展形式．

参考文献：

［1］Black F,Scholes M S.The Pricing of Options and Corporate Liabilities［J］.Journal of Political Economy,1973,81(3):637-654.

［2］Duffie.Security Markets:Stochastic Models［M］.New York:Academic Press,1988.

［3］俞迎达,俞苗.Black-Scholes期权定价模型的简化推导［J］.数学的实践与认识,2001,31(6):756-758.

［4］邓乐斌.Black-Scholes期权定价公式的两种简化推导［J］.中国水运：理论版,2006,4(5):164-165.

［5］潘冠中,马晓兰.期权定价Black-schloes公式的一个新推导［J］.经济数学,2012,29(2):57-60.

［6］侯迎春.认证股权定价模型和方法及在我国的应用研究［D］.北京:对外经济贸易大学,2007.

［7］陈万义.非风险中性定价意义下的欧式期权定价公式［J］.数学的实践与认识,2004,34(1):76-79.

［8］王峰,徐小平,赵炜.布朗运动和泊松过程共同驱动下的欧式期权定价［J］.纯粹数学与应用数学,2004,20(1):79-83.

［9］苏军,赵选民,王雪峰.Black-Scholes期权定价模型的一种改进方法［J］.西南民族大学学报:自然科学版,2005,31(4):504-507.

［10］闫海峰,刘三阳.带有Poisson跳的股票价格模型的期权定价［J］.工程数学学报,2003,20(2):35-40.

［11］闫海峰,刘三阳.广义Black-Scholes模型期权定价新方法——保险精算方法［J］.应用数学和力学,2003,24(7):730-738.

［12］闫海峰,翟永会,刘三阳.股票价格遵循几何分式Brown运动的期权定价［J］.数学的实践与认识,2006,36(8):19-24.

［13］孙玉东,师义民.修正的Black-Scholes模型下的欧式期权定价［J］.高校应用数学学报,2012,27(1):23-32.

［14］FAN Kun.Pricing Options under Two-Factor Markov-Modulated Stochastic Volatility Models［J］.Chinese Journal of Applied Probability and Statistics,2014,30(6):620-630.

［15］任智格,何朗,黄樟灿.一种无风险利率时变条件下的Black-Scholes期权定价模型［J］.数学杂志,2015,35(1):203-206.

［16］薛红,王拉省.分数布朗运动环境中最值期权定价［J］.工程数学学报,2008,25(5):843-850.

［17］薛红,孙玉东.分数跳-扩散过程下亚式期权定价模型［J］.工程数学学报,2010,27(6):1009-1014.

［18］李志广,康淑瑰.美式期权定价的有限体积元方法［J］.系统科学与数学,2012,32(9):1092-1108.

［19］顾锋娟,岑仲迪,乐安波.美式分期付款期权定价模型的有限差分法［J］.工程数学学报,2013,30(6):791-803.

［20］彭斌,彭菲.基于跳-分形模型的美式看涨期权定价［J］.数学的实践与认识,2014,44(24):1-9.

［21］王伟,苏小囡,赵奇杰.马尔可夫调制的跳扩散过程下远期生效看涨期权的定价［J］.应用概率统计,2014,30(6):585-597.

［22］SU Xiao-nan,WANG Wei,WANG Wen-sheng.Valuing power options under a regime-switching model［J］.Journal of China Normal University:Natural Science,2013,30(6):32-39.

［23］王嘉展,刘丽霞.随机利率下股票价格服从几何分数布朗运动的幂期权定价［J］.河北师范大学学报:自然科学版,2014, 38(2):113-116.

［24］袁国军,肖庆宪.基于近似对冲的亚式期权定价模型与实证分析［J］.上海理工大学学报,2014,36(5):416-424.

［25］唐玲,林志超.随机波动率模型下几何平均亚式期权的定价［J］.沈阳大学学报:自然科学版,2014,26(6):510-513.

（责任编辑：邵晓军）

中图分类号：O29；F830.9

文献标识码：A

文章编号：1007-5348（2015）08-0008-05

［收稿日期］2015-04-27

［作者简介］王明辉（1986-），男，山东济宁人，韶关学院数学与统计学院助教，硕士；研究方向：线性模型．

An Overview of the Deductive Method and Extensions of Black-Scholes Formula

WANG Ming-hui
（School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China）

Abstract:From the background of theory and assumed condition of Black-Scholes formula,the paper first in

troduces the derivation of the option pricing formula,then it recommends several deductive approaches used by scholars from home and abroad,finally it presents the promotion of the Black-Scholes model from two aspects, namely the easing of the assumptions and the expansion of the option model.

Key words:Black-Scholes model;option pricing formula;extensions