UCT算法在不围棋博弈中的实现

梁国军，谢垂益，胡伶俐，林　　昊，李景炤

（韶关学院 数学与统计学院，广东 韶关5120051）

UCT算法在不围棋博弈中的实现

梁国军，谢垂益*，胡伶俐，林昊，李景炤

（韶关学院 数学与统计学院，广东 韶关5120051）

摘要：计算机博弈是人工智能领域的挑战性课题，它利用计算机进行分析、判断和推理，从而得到理性的决策.不围棋是近年来计算机博弈竞赛的一个棋种，属于围棋的变体，其规则是先吃子或棋子自杀的一方为负.通过分析不围棋博弈模型的特点，提出了对上限信心界树搜索(UCT)算法的一个优化方法，在算法的启动过程优先选择评分较高的盘面进行模拟博弈，以便得到更好的落子选择.在与著名的OASE-NoGo软件的试验对弈中，以该算法为核心设计的不围棋软件取得了90%以上的胜率，证明是可行、有效的.

关键词：人工智能；计算机博弈；不围棋；UCT算法

棋类游戏是计算机博弈领域的重要研究课题，这些研究工作有助于加深对人工智能与计算机科学的认识，促进对人类认知过程的理解.不围棋是十多年前开始出现的一种双人博弈游戏，属于围棋的变体，如果一方落子后吃掉了对方的棋子、或者令已方棋子自杀，则落子一方判负［1］.2011年起，由国际计算机博弈协会（International Computer Games Association，ICGA）组织的计算机奥林匹克（Computer Olynpiad）大赛增加了不围棋项目.2012年起，由中国人工智能学会举办的中国机器博弈锦标赛也将不围棋列入比赛项目.在这些高级别赛事的推动下，不围棋正在为人们认识并开始进行研究.

笔者总结了不围棋的研究现状，分析了不围棋的博弈模型，给出上限信心界树搜索 （UCT，UCB for Tree Search）中的UCB1子算法的一个修正，使其能更早地选择优势盘面，并据此设计了一个不围棋博弈软件，通过与对照软件的对弈实验来验证算法的有效性.

1　　研究现状

早些年，计算机博弈对于棋类游戏的研究集中在基于模式识别和专家系统的方法上（最典型的是基于静态评估函数的α-β博弈树方法），并在国际象棋、中国象棋等项目中获得了成功.但是对于围棋类的项目，由于搜索空间巨大只能访问博弈树的一小部分、无法进行准确的静态盘面评估，因此传统的方法一直无法取得满意的结果，在2000年前后，世界上最高水平的计算机围棋软件的棋力还比不上人类的业余初段.2006年，Levente Kocsis和Csaba Szepesvári将蒙特卡洛树搜索（Monte-Carlo Tree Search，MCTS）方法与UCB公式［2］结合，提出上限信心界树搜索（UCT，UCB for Tree Search）算法［3］，显著地提高了搜索效率. UCT算法的出现开创了计算机博弈研究的新局面.此后人们围绕MCTS方法进行研究和改进，推动围棋软件的棋力不断提高.2013年3月，围棋软件CrazyStone在受让四子的情况下，战胜日本棋手石田芳夫九段，其棋力已达到业余五、六段的水平.

首次对不围棋的研究报道出现在2011年，文献［4］介绍了MCTS算法在不围棋中的实现.通过对比测试发现，在围棋中常用的快速动作值估计（Rapid Action-Value Estimates，RAVE）、节点慢速创建、布局模板、UCT等方法和算法，在不围棋中同样有效；文献［5］提出一个结合本体、进化计算、模糊逻辑、模糊标记语言的遗传算法，根据收集的棋局模式和预构建的不围棋模糊本体，用基于模糊推理机制的遗传模糊标记语言分析当前棋局，得到下一个最好的棋步，并应用了遗传学习机制，可在与参照棋局的对垒中不断提高棋力；文献［6-7］分析了棋局模板的分类和格式定义，在对弈过程中优先使用模板进行棋步的选择，当出现模板中没有的棋局时再使用MCTS算法；文献［8］提出在对弈过程中进行UCT树的重用，可以增加5%～30%的搜索深度；文献［9］通过启发式、暴力搜索、参数调整等方式，提高UCT算法的搜索成功率；文献［10］提出在MCTS算法中增加静态估计方法，根据周围棋子的类型标记出允许自由落子的点和禁止落子的点，加快博弈树搜索速度.

由于不围棋是新的棋类，相关的研究成果较少.目前对不围棋的主要研究方法是参考棋类尤其是围棋的相关理论和技术，根据其博弈规则进行改造和拓展.但由于博弈规则不同，博弈模型的建立、盘面优势评估、博弈树搜索等过程相较其他棋类有很大的区别.对于不围棋博弈的研究，大多内容都将会是创新性的工作.

2　　不围棋的博弈模型

一个不围棋的博弈模型包括对弈规则［9］、博弈树的生成、盘面评估、博弈搜索算法等内容.

2.1博弈树的生成

9路不围棋的盘面有9行9列，总共81个点.在双人对弈过程中，先手方要考虑的落子点依次为81、79、77、……、3、1个，后手方要考虑的落子点依次为80、78、76、……、4、2个.对于选手在第i步（先手时1≤i≤41，后手时1≤i≤40）时，若考虑连续的d步落子（从本步算起），则可供选择的盘面数R为：

根据式(1)，表1列出选手在盘中下完第20步后，考虑第21步开始的连续2、5、10步落子时需要检查的盘面数.

表1　　盘中第21步起的盘面数

以当前的盘面作为根结点，后续d步的可选盘面构成子树结点，形成一个d+1层的博弈树.计算机通过搜索该博弈树得到下一步落子的最优选择.

从下棋的经验中知道，能够预估的后续落子步数(d)越多，棋手的棋力就越强，获胜的概率越高，计算机博弈也是如此.但当考虑过多的后续步（例如5步以上）时，博弈树中的结点数量过于庞大、呈指数级增长，对于普通计算机来说，需要较多的计算时间和存储空间，容易出现落子过慢、内存不足的情况.

2.2盘面评估

下面先给出气、眼、虎口、禁入点等基本术语的定义．

定义1：气指与棋子/棋块相邻的空白点.

定义2：眼指同种颜色的棋子围成的一个空白点，相当于棋块内的“气”.对方如果在该眼位落子，则该棋子的气为0，形成一种自杀行为.

定义3：虎口指这样的一个空白点，落在该点的棋子的气为1.虎口是最接近完成眼之前的一个状态.定义4：禁入点指能使对方的棋子或棋块无气的一个未落子的点.若在禁入点落子，将杀死对方的棋子或棋块，本方直接判负.

在对弈过程中，每走一步棋，应使己方的合法落子点尽量多、对方的合法落子点尽量少，这样就越有机会接近胜利.根据不围棋的对弈规则，对弈过程中应使已方盘面中的眼和虎口的数量尽量多、禁入点的数量尽量少.因此，定义盘面N的评估函数S(N)为：

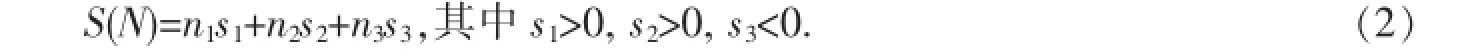
式（2）中，n1为盘面N中眼的个数，s1为每个眼的分值，n2为虎口的个数，s2为每个虎口的分值，n3为禁入点的个数，s3为每个禁入点的分值.S(N)的值越大表明盘面越有利，否则盘面状态越不理想.

2.3博弈搜索算法

在不围棋博弈中，假设双方总是采用最佳的落子策略.最佳的落子策略是指选手在任意给定的盘面中，如果存在致胜的走法，则选手就会选择致胜的走法落子.给定任意的盘面状态，总是可以构建、遍历博弈树，然后总能找到最佳落子点，使该选手取得胜利，所以不围棋是可解的.

由于不围棋博弈树的规模非常大，即使模拟数百万次的对局，也仅仅能够覆盖博弈树很小的一部分.如果随机地选择博弈树的子节点，则会花费非常多的搜索空间和时间，使得搜索的效率低下.建议在子节点的随机模拟过程中加入不围棋知识的各种策略，进而得到更高的搜索效率和更准确的结果.

博弈搜索算法的基本思路是：给定一个任意盘面和某一选手的棋子颜色，建立博弈树，进行搜索、评估和剪枝，返回评估分值最好的一条路线.

3　UCT算法的设计

UCT算法是UCB算法与蒙特卡洛方法的结合.笔者提出对UCB算法的一个修正，据此对UCT算法进行优化设计.

3.1蒙特卡洛方法

蒙特卡洛方法的主要理论基础是大数定律，在随机取样的情况下，可以获得有误差的评估值，取样的数量越多，误差将越小，评估值将越准确.运用蒙特卡洛方法模拟不围棋中随机落子的步骤是：保存当前棋盘状态，生成下一步所有可落子点，选一可落子点落一子，接着按对应黑白子落子的顺序，黑子和白子轮流随机落子，直至分出胜负.记录胜负和模拟次数，恢复棋盘至之前保存状态.重复多次模拟以提高准确性，直至模拟到时间结束或者到达规定的模拟次数为止，选择胜率最大的可落子点，该点为最佳落子点.蒙特卡洛方法算法的伪码为：

MonteCarlo(棋盘状态){

根据棋盘状态生成下一步所有可落子点；while(模拟时间未到或者未达到模拟次数){黑子和白子轮流随机落子，直至分出胜负；记录胜负和模拟次数；

更新相关节点的方向次数和获胜的次数信息值；}返回胜率最大的可落子点；}.

3.2 UCB算法的修正

UCB算法来源于多臂匪徒模型，它采用在线的机器学习策略，既对当前已有知识进行利用，又有对未了解的知识进行探索.这当中最著名的是UCB1算法［2］，其核心是信心上界索引计算公式(UCB1公式)：

式中N为博弈树中的给定节点，Ni为N的子节点，I(Ni)为Ni的信心上界索引，t(N)为对N的模拟次数，t (Ni)为Ni在模拟中被选中的次数，X(Ni)为Ni的收益平均值.C为加权系数，如果C比较小则表明当前的搜索偏重于利用；C比较大则说明当前搜索偏重于探索.

UCB1算法采取随机的方式开始第一步的选择.但是对于棋类博弈的情形，当处于盘中某一个对弈盘面时，可以根据对盘面的评估，优先选择往有利方向发展的落子.因此，本文提出对UCB1算法的修正思路：对于博弈树中的子结点Ni（对应一个可能的盘面)，先按式(2)进行盘面评估，评估结果作为Ni的收益初始值X1(Ni.由于在棋类博弈中Ni的收益平均值往往取为该节点对应盘面的胜率，是一个不大于1的数字，因此可事先设定一个极大值常数M，使得S(Ni)/M小于1.经过修正的UCB算法伪码为：

UCB_modify(棋局盘面N){//得到盘面N的下一步可落子点if(N无孩子结点){//创建下一层博弈树

下一步的所有可落子点Ni作为N的孩子结点；

＜--盘面评估值S(Ni)/M；}

Else{//访问下一层博弈树

循环：遍历访问N的所有下一步可落子点Ni，用公式(3)计算；}

返回值最大的子节点Ni；}.

3.3优化的UCT算法

通过蒙特卡洛方法可以解决不围棋落子搜索的问题，但是因为蒙特卡洛方法是随机模拟的，而且没有先验知识的指导，使得博弈树的可扩展层数较少，很难得到最优解.UCT算法的基本思想是将UCB算法应用到蒙特卡洛规划过程中，通过计算UCB值来选择落子点，不再是随机选择，有利于更早得到最优解.但是UCB算法的初始阶段还是通过随机选择落子点启动模拟对弈过程，没有考虑盘面的差异对胜负趋势的影响.本文根据修正的UCB算法实现对UCT算法的优化，使得盘面局势影响落子位置，盘面评估得分较高的位置落子的机会更大，而盘面评估结果较差的落子位置也会有机会被选中、只是优先级比较低.该UCT算法伪码为：

UCT(棋局盘面root){//根据棋盘状态返回一个落子点

建第一层博弈树，以下一步的所有可落子点作为root的孩子结点；

node［0］＜--root；

while(模拟时间未用完或者未达到模拟次数){

i＜--0；

while（node［i］不是终局盘面){//向下扩展，创建或访问多层博弈树

i++；

node［i］＜--UCB_modify(node［i-1］)；//选出下一步可落子点

}

value＜--对node［i］的评判结果（取胜为1、负为0）；

若i为偶数，value＜---value；//偶数次是对方的落子，相应获胜数取负值以便区分

for(j=i-1；j＞0；j--){//向上更新父节点的获胜数和模拟次数

value＜---value；

node［j］的获胜数增加value、模拟次数增加1；}

}pos＜--胜率(获胜数/模拟次数)最高的可落子点(root的某个孩子结点)；

删除以root为根的博弈树；

返回pos；}.

4　　实验结果

根据上述的UCT算法，实现了一个不围棋博弈软件，并通过与著名的台湾大学不围棋软件OASE-No-Go V1.1进行对弈测试实现效果.

与OASE-NoGo V1.1的初级棋的对弈结果见图1，与OASE-NoGo V1.1的高级棋的对弈结果见图2.

图1初级对弈结果　

图2高级对弈结果

表2为与OASE-NoGo V1.1初级和高级对弈的结果记录，可以看出，本文实现的不围棋博弈软件有较强的棋力，在与对照软件的对弈中，取得了90%以上的胜率.

表2　　对弈结果记录表

5　　结论

针对不围棋博弈模型的特点，对UCT算法中的UCB子算法进行了修正，将盘面评估结果作为算法启动时的初始值，优先选择较优的盘面进行模拟对弈，以便更快得到较好的棋步.所有的盘面都有机会被选中，只是较差的盘面被选中的概率较低而已.UCT算法的“利用已知、探索未知”的特性仍然得以保留.在与著名的不围棋软件OASE-NoGo V1.1的多次对弈实验中，以上述算法为核心实现的不围棋博弈软件取得了90%以上的胜率，结果证明该算法可行、有效.

参考文献：

［1］Denim S.Anti Atari Go［EB/OL］.(2011-12-07)［2014-8-30］.http://senseis.xmp.net/?AntiAtariGo.

［2］Auer P，Cesa-Bianchi N，Fischer P.Finite-time Analysis of the Multiarmed Bandit Problem［J］.Machine Learning，2002，47(2-3):235-256.

［3］Kocsis L,Szepesvári C.Bandit based monte-carlo planning［C］.//Proceedings of the 17th European conference on Machine Learning, Berlin in Germany:Springer-Verlag,2006:282-293.

［4］CHOU C W,Teytaud O,and YEN S J.Revisiting Monte-Carlo tree search on a normal form game:NoGo［C］.//Proceedings of the 2011 international conference on Applications of Evolutionary Computation,Torino in Italy:Springer-Verlag,2011:73-82.

［5］LEE C S，WANG M H，CHEN Y J，et al..Genetic fuzzy markup language for game of NoGo［J］.Knowledge-Based Systems，2012(34): 64-80.

［6］SUN Y X,LIU C,and QIU H K.The research on patterns and UCT algorithm in NoGo game［C］.//25th Chinese Control and Decision Conference,Guiyang:IEEE,2013:1178-1182.

［7］SUN Y X,WANG Y J,and LI F.Pattern matching and Monte-Carlo simulation mechanism for the game of NoGo［C］.//Proceedings of IEEE CCIS2012,Hangzhou:IEEE,2012:61-64.

［8］LI R,WU Y Q,ZHANG A D,et al.Technique analysis and designing of program with UCT algorithm for NoGo［C］.//25th Chinese Control and Decision Conference,Guiyang:IEEE,2013:923-928.

［9］佘博玄，禁围棋程式设计与研究［D］.台湾新竹：交通大学，2013.

［10］SUN Y X,RAO G J,SUN H M,et al.Research on static evaluation method for computer game of NoGo［C］.//26th Chinese Control and Decision Conference,Changsha:IEEE,2014:3455-3459.

（责任编辑：欧恺）

中图分类号：TP312

文献标识码：A

文章编号：1007-5348（2015）08-0017-04

［收稿日期］2015-05-15

［基金项目］国家级大学生创新创业训练计划项目(201410576018)；广东省大学生创新创业训练计划项目(201410576060)；韶关学院科研项目(2012-16).

［作者简介］梁国军(1992-)，男，广东清远人，韶关学院数学与统计学院本科生；研究方向：计算机算法.*通讯作者.

An Implementation of UCT Algorithm for NoGo Game

LIANG Guo-jun,XIE Chui-yi,HU Ling-li,LIN Hao,LI Jing-zhao
（School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China）

Abstract：Computer game is a challenging task in the field of artificial intelligence,which makes use of com

puter to analyze,judge and reason,so as to get the rational decision.In recent years,NoGo game is a kind of computer game competitions,similar to the game of Go,with the rules of no capture or suicide which is allowed. According to the characteristics of NoGo game model,an optimized UCT(UCB for Tree Search)algorithm is pro

posed to compute the better move by choosing certain chess layout with high score preferentially.A NoGo game software is designed mainly relies on the above-mentioned algorithm and proved to be feasible and efficient by the result of achieving more than 90%of winning with the famous OASE-NoGo.

Key words：artificial intelligence;computer game;NoGo;UCT algorithm