线性回归分类器在模式识别中的应用
徐 洁,祝文康(1.广东工业大学 智能信息处理实验室,广东广州510006;.韶关学院数学与统计学院,广东韶关51005)
线性回归分类器在模式识别中的应用
徐洁1,2,祝文康2
(1.广东工业大学 智能信息处理实验室,广东广州510006;2.韶关学院数学与统计学院,广东韶关512005)
摘要:线性回归分类器(LRC)在人脸识别上呈现出了优越的性能,然而,随着每类的训练样本数量增大,LRC的分类速度变得很慢.除此之外,LRC还有一致命的弱点:对大样本问题束手无策,即当每类用于训练的样本数量大于样本的维数时,LRC无法工作.解决以上问题的一个行而有效办法是对LRC作局部化处理.可以对LRC作了两类局部拓展:一是基于K最近邻的线性回归分类器(KNN-LRC).KNN-LRC借助KNN算法对每类训练的样本作了筛选,从而避免了大样本问题的出现,但却受到近邻参数选择的困扰.二是在此基础上进一步提出了基于L1范数的自适应局部线性回归分类器(LI-LRC).L1-LRC具有自适应的近邻选择机制,同时能取得比KNN-LRC更好的分类性能.在两个数据库上,比较各种相关分类器的性能.从分类的结果来看,KNN-LRC和L1-LRC较其它相关分类器的性能好.
关键词:线性回归分类器;局部;K最近邻;L1正则化;模式分类
最近,Naseem等人提出了线性回归分类器(LRC)并将其成功应用在人脸识别问题上[1].LRC分类的基本思想是为测试样本寻找最好的类重构,即具有最好的类重构的类别即被认为是测试样本的类别所在.从文献[1]报告的实验结果来看,LRC确实获得了令人鼓舞的结果.然而,当每类用于训练的样本数量很大时,LRC时耗大.除此之外,由于LRC是专门为类似人脸识别的小样本问题[2-3]而设计的,故当面对大样本问题,LRC无力可施.
为克服LRC的不足,笔者提出两类局部的线性回归分类器.一类是K最近邻线性回归分类器(KNNLRC).与LRC对比,KNN-LRC需要额外增加一个近邻选择的步骤.换而言之,KNN-LRC是在所选择的近邻上执行LRC.尽管只是对LRC作了局部处理,但KNN-LRC取得了比LRC更好的分类性能,同时通过对近邻参数的调节,KNN-LRC避免了大样本问题的出现.但像许多局部的方法一样,KNN-LRC同样面临着如何选择最佳近邻参数的困扰.为解决此类问题,Wang等人和Mekuz等人在做了很多的尝试,并给出了相应的解决办法[4-5].
除KNN-LRC外,本文还提出另外一类局部线性回归分类器,自适应的局部线性回归分类器 (L1-LRC).与KNN-LRC不同,L1-LRC不需要事前人为地把近邻参数设定,而是在LRC原有的目标优化上对回归系数增加L1范数正则化约束.因此,L1-LRC也被认为是带惩罚的最小二乘法,它同时实现了系数的连续收缩和自适应的变量选择.由此得到的回归系数是稀疏的.而非零项的回归系数所关联的样本有着相似的特征,因此也被认为是测试样本的相似近邻.L1-LRC的这一特点提供了相似近邻的自适应选择机制.
1 局部线性回归分类器

1.1 K最近邻局部线性回归分类器(KNN-LRC)


其中,βi=[βi,1,βi,2,…,βi,k]T是y在第i类的回归系数向量.
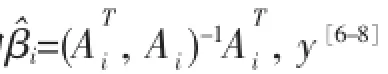

如果ds(y)=mindi(y),y则被分到第s类.
1.2自适应的局部回归分类器(L1-LRC)
通常,如果测试样本属于第i类,该测试样本能很好地被同类的样本线性表示.在LRC原有的目标优化下,增加对回归系数作L1范数正则化约束.最佳的回归系数向量可通过求解:

得到.但由于在现实的应用中,可提供的训练样本数量十分有限,同时数据采集过程中容易混入噪声和离群点,故y=Xβ很难实现.为此,放松公式(3)约束条件如下:

为方便计算,选择公式(4)来求解最佳的回归系数.现存的许多Matlab代码可直接用于求解.有一点值得注意,与KNN-LRC不同,由公式(4)求解得到的回归系数是稀疏的.当正则化参数λ增加时,β只有很少一部分的项非零.由于非零项所关联的样本与测试样本有着相似的特征,因此被认为是测试样本的“相似”近邻.由此看来,L1-LRC具有自适应的近邻选择机制.
1.3KNN-LRC和L1-LRC与LRC的优劣性比较


1.4KNN-LRC和L1-LRC以及LRC的计算复杂性


图1 一个关于正则化方法可行的演示
2 仿真实验
为进一步检验KNN-LRC和L1-LRC的算法性能,在UCI的Wine数据库和CENPARMI手写阿拉伯数字库上分别比较了KNN-LRC和L1-LRC与最近邻分类器(NNC)[10],最小距离分类器(MDC)[11],线性回归分类器(LRC)[1]和稀疏表示分类器(SRC)[12]的性能.实验中,采用“l1_ls”[13]来求解SRC.L1-LRC中的正则化参数和KNN-LRC中的近邻参数K均采用全局到局部的搜索方法来设定.
2.1在UCI Wine数据集上的实验
来自于UCI的Wine[14]数据集共有13个特征,3个类别,共178个样本.每类选取48个样本用于实验. 在UCI Wine数据集中随机选取T=(30,40)幅图像用于训练,剩余图像用于测试.每组实验运行10次.NNC、MDC、SRC、LRC、KNN-LRC和L1-LRC直接用于分类,最大的平均识别率和相应的标准方差记录在表1和表2记录了各种方法的运行时间.


表1 当T(=30,40)时,各种方法的最大平均识别率和相应的标准差

表2 各方法10次实验的平均运行时间 (单位:s)
为更进一步考察近邻参数对KNN-LRC分类性能的影响,图2给出了随近邻参数变化的KNN-LRC识别率曲线变化.观察图2不难发现:当每类的训练样本数为30或40时,KNN-LRC分别在K=8和K=5时取得最高的识别率.随着近邻参数K的不断增大,KNN-LRC的性能出现下降的趋势.尤其是当K>12时,两类情况的识别率都少于40%.由此可见参数的选择对KNN-LRC的性能有一定的影响.再来观察L1-LRC的近邻数,训练样本不同,近邻参数也不一样;即便每类用于训练样本数量一样,不同类样本采用的近邻参数也不尽相同.可见,L1-LRC具有近邻参数的自适应选择机制.
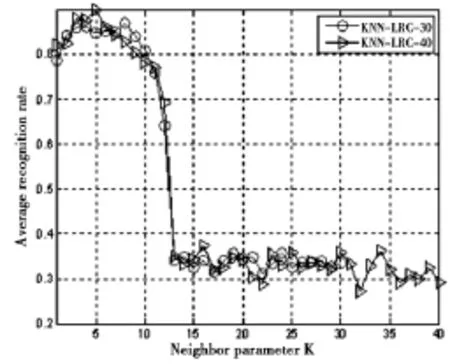
图2 不同近邻参数下KNN-LRC的识别率变化曲线

表3 L1-LRC的近邻参数是10次实验的平均结果及其标准差
2.2在CENPARMI手写阿拉伯数字库上的实验
CENPARMI手写阿拉伯数字库包含10个类的6 000个从“0”到“9”的121数字图像[15].本实验选取个图像用于训练,剩余的样本用于测试.6种分类器直接对121维的样本图像进行分类.表4列出了每种方法的最大识别率和相应的近邻参数和每种方法的运行时间.图4是KNN-LRC随近邻参数K变化的识别率曲线图.
观察表4,以及图4和图5,可以发现:(1)KNN-LRC和L1-LRC要比NNC、MDC、SRC和LRC的分类性能要好;(2)当T=(30,50)时,LRC的分类性能并不差,这结果与在UCI Wine数据库上所做的实验反差很大.相对于UCI Wine数据库的样本,在CENPARMI手写阿拉伯数字库的样本的维度要比每类用于训练的样本数量要大,这是典型的小样本问题.而LRC是为类似人脸识别的小样本问题而设计,因此在该类情况下,LRC的分类效果要比NNC、MDC和SRC好.但是当每类用于训练的样本数达到130时,LRC出现了在UCI Wine数据集上的类似问题,只取得了10%的识别率.与LRC对比起来,KNN-LRC和L1-LRC对训练样本数量无具体要求,也表现得更为稳定;(3)当每类用于训练的样本达到130时,MDC遭受了在UCI Wine数据库的同样情况;(4)观察表4关于SRC的实验结果,当用于训练的样本数越大,SRC取得的分类性能越好.当T=130,SRC的识别率是91.6%,这比NNC、MDC和LRC的要高.SRC能取得如此好的分类结果,可归功于SRC其自身的分类准则.SRC力求为每个测试样本找到最能对其进行稀表示的类别所在.当训练样本数达到130时,这为SRC提供的充足的训练样本,非常有利于稀疏重构.尽管如此,SRC还是要逊色于L1-LRC和K1-LRC;(5)KNN-LRC的分类性能与近邻参数K的选择有着紧密的联系,就图4所示结果,可以发现当时,KNN-LRC最好的实验结果是在K=10取得,随着K增加到60,KNN-LRC的识别率只有65%.由此可见,KNN-LRC对近邻参数的选择很敏感;(6)从表5的运行时间来看,KNN-LRC要比LRC快;L1-LRC要比KNN-LRC慢,却比SRC要快.

表4 在CENPARMI手写阿拉伯数字库上,各种方法的最大训别率和运行时间

图4 在CENPARMI手写阿拉伯数字库上,不同近邻参数下KNN-LRC的识别曲线图

图5 在CENPARMI手写阿拉伯数字库上,NN-LRC和L1-LRC的每类样本的近邻参数的变化
3 结语
本文提出两类局部的线性回归分类器:KNN-LRC和L1-LRC.KNN-LRC和L1-LRC很好地克服了LRC的不足,并取得了不错的分类性能,这在UCI Wine数据库和CENPARMI手写阿拉伯数字库上得到很好的验证.
参考文献:
[1]Naseem I,Togneri R,Bennamoun M.Linear regression for face recognition[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2010,32(11):2106-2112.
[2]Fukunaga K.Introduction to statistical pattern recognition[M].New York:Academic press,2013.
[3]Chen L F,Liao H Y M,Ko M T,et al.A new LDA-based face recognition system which can solve the small sample size problem[J].Pattern recognition,2000,33(10):1713-1726.
[4]Zhang Z,Wang J,Zha H.Adaptive manifold learning[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2012, 34(2):253-265.
[5]Mekuz N,Tsotsos J K.Parameterless Isomap with adaptive neighborhood selection[M].Berlin:Pattern Recognition Springer Berlin Heidelberg,2006:364-373.
[6]Hastie T,Tibshirani R,Friedman J,et al.The elements of statistical learning[M].New York:springer,2009.
[7]Seber G A F.Linear Regression Analysis[M].New York:Wiley-Interscience,2003.
[8]Ryan T P.Modern Regression Methods[M].New York:Wiley-Interscience,1997.
[9]Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM journal on scientific computing,1998,20 (1):33-61.
[10]Cover T,Hart P.Nearest neighbor pattern classification[J].Information Theory,IEEE Transactions on,1967,13(1):21-27.
[11]Gonzalez R C,Woods R E.Digital Image Processing[M].New York:Addison Wesley,1997.
[12]Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sparse representation[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2009,31(2):210-227.
[13]Kim S,Koh K,Lustig M,et al.A method for large-scale l1-regularized least squares problems with applications in signal processing and statistics[J].IEEE J.Select.Topics Signal Process,2007.
[14]Blake C L,Merz C J.Repository of machine learning databases[EB/OL].(1998-01-05)[2015-03-21].http://www.ics.uci.edi/mlearn/ MLRepositery.html.
[15]Suen C Y,Nadal C,Legault R,et al.Computer recognition of unconstrained handwritten numerals[J].Proceedings of the IEEE, 1992,80(7):1162-1180.
(责任编辑:邵晓军)
中图分类号:TP301.6
文献标识码:A
文章编号:1007-5348(2015)08-0001-07
[收稿日期]2015-05-12
[基金项目]国家自然科学基金(61305036);中国博士后基金(2014M560657).
[作者简介]徐洁(1979-),女,广东韶关人,韶关学院数学与统计学院助理研究员,博士;研究方向:数据挖掘、计算机视觉、智能信息处理.
Local Linear Regression Classifiers for Pattern Classification
XU Jie1,2,ZHU Wen-kang2
(1.Intelligent Information Processing Lab,Guangdong University of Technology,Guangzhou 510006,Guangdong, China;2.School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China)
Abstract:The linear regression classifier(LRC)has been developed and shows great potential for face recognition.However,when the size of training sample per class is large,LRC is time-consuming.Moreover,LRC cannot be applied to the large sample size cases.To solve these problems,the paper develops two local approaches. One is the K-nearest neighbor based linear regression classifier(KNN-LRC),which regresses the testing sample onto its K-nearest neighbors in each class,instead of the whole set of training samples per class.Due to the relative smaller K compared to the number of training samples per class,KNN-LRC runs faster than LRC.In addition,by tuning K,LRC can be performed in any cases,even in the large size sample cases.However,with the common K the performance of KNN-LRC is suboptimal.It further develops the auto-adaptive local regression classifier(L1-LRC),which actually is LRC with a constraint of the L1-norm regularization on the regression coefficients.L1-LRC provides a mechanism of adaptive neighbor selection,and achieves better performance than KNN-LRC.These two local classifiers are evaluated on the three public available databases.Experimental evaluation shows that the proposed methods performe better than the state-of-the-art methods.
Key words:linear regression classifier;locality;K-nearest neighbors;L1 regularization;pattern classification

