基于MF预编码的大规模MIMO网络SINR概率密度分析*
束 锋 李 隽 顾 晨 王 进 周 叶 徐彦青 钱玉文
(1.南京理工大学电子工程与光电技术学院,南京,210094;2.东南大学移动通信国家重点实验室,南京,210096;3.南京理工大学近程高速目标探测技术国防重点学科实验室,南京,210094)
引 言
近年来,随着智能手机的广泛普及与移动互联网的快速发展,人们对无线数据传输速率的要求显著增加。传统的小规模多用户多输入多输出(Multiple-input multiple-output,MIMO)技术由于具备较高的频谱效率,已经被4G标准采纳为关键技术之一。功率分配和波束成形是传统小规模多用户MIMO系统的两种关键技术[1-11]。前者可明显提高系统的可靠性[1-3],而后者可有效减少多用户间的干扰,显著提高系统的信息传输速率[4-11]。发射端波束成形的代表算法有匹配滤波(Matched filter,MF)、迫零(Zero forcing,ZF)[4-5]、块对角化(Block diagonalization,BD)[6]、最大化信泄噪比(Maximum signal-toleakage-and-noise ratio,Max-SLNR)[7]、特征值分解[8]、最小均方误差(Minimum mean square error,MMSE)[9-10]和酉速率控制[11]。
大规模MIMO相比于小规模MIMO,可进一步显著提高频谱效率,正在日益受到关注,现已成为无线通信领域的热点研究方向之一,并被视为下一代无线通信的关键技术之一。不仅如此,大规模MIMO技术可以用较低的功耗提供很高的频谱效率,因此,非常适合于绿色无线通信[12-14]。传统小规模多用户MIMO的波束成形及功率分配可以推广到大规模多用户MIMO系统中,但其中基于信道矩阵分解的一类发射波束成形算法,如BD,Max-SLNR,MMSE,ZF需要大约KN3次数的复乘运算(其中,K为用户数,N为基站发射天线数),当基站天线数达到几百或几千副时,它们的复杂度就变得相当巨大。文献[15]考虑消除多用户大规模MIMO系统中的较大干扰项,以简化ZF预编码器的复杂度。文献[16]则采用二项式分解降低ZF预编码中矩阵求逆的复杂度,同时优化相关系数,以最大化多基站MIMO系统的信干噪比(Signal-to-interference-and-noise ratio,SINR)。然而,这些改进算法要达到与原有算法相近的误码性能或和速率性能,运算的复杂度就要远高于MF预编码的复杂度KN次复乘运算。MF作为低复杂度的预编码器,在N为大规模时将与其他预编码趋于同样的和速率[12-15],因而在大规模MIMO中极具实用潜能。考虑到MF在大规模MIMO中具有较强的实用性,文献[17]推导了在该环境下采用MF预编码的SINR的近似概率密度函数(Probability density function,PDF)表达式。但文献[17]着重考察高信噪比下MF预编码的近似PDF,对低信噪比下噪声与干扰相当的情况研究较少,因此本文针对一般信噪比下的大规模MU-MIMO环境,推导了MF预编码近似SINR的PDF,并通过仿真验证所推导的公式的准确性。
1 系统模型
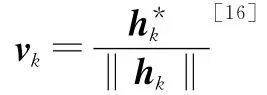
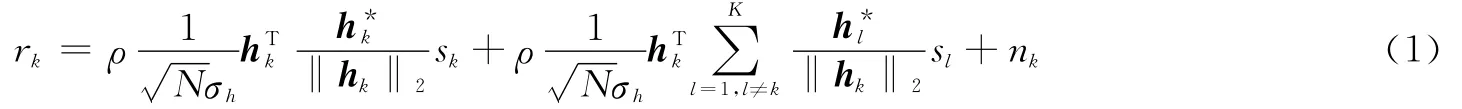
式中:ρ定义为基站的总发射功率,sk和sl分别表示基站发送给用户k和用户l的数据符号,nk是均值为0且方差为的加性白高斯噪声。用户k的SINR可表示为


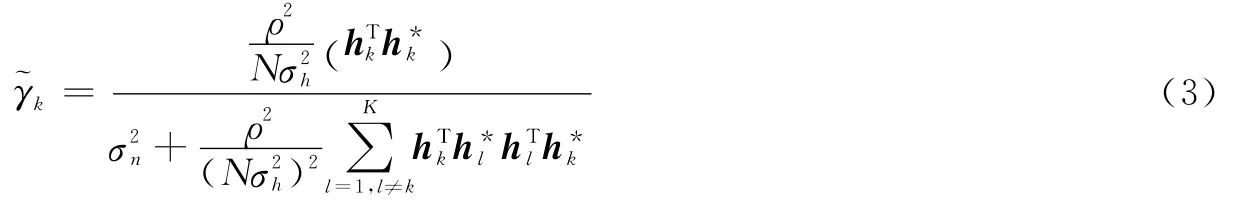
基于式(1,3),易获得所有用户的和速率为

2 信干噪比的近似概率密度函数
为了便于推导式(3)定义的SINR的PDF,首先定义两个新的随机变量

和

则式(3)可简化为

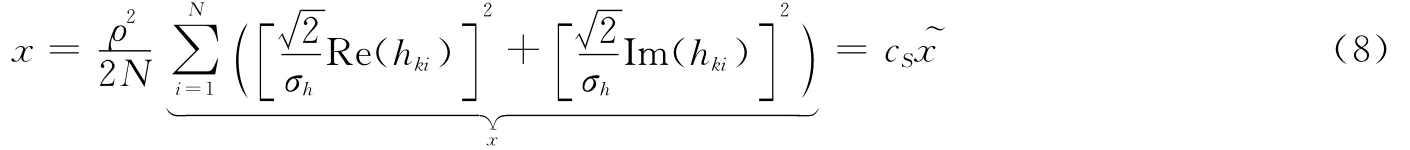


式中≥0,且

依据式(8,9),可获得x的概率密度函数

下面推导yl的概率密度函数。根据式(6),yl可展开为

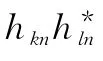
若k≠l或n≠m,则hkn与hlm相互独立,它们的积也相互独立。因此,对所有k≠l或n≠m,有

式(12)所示的yl的统计平均值为

随机变量yl的方差定义为
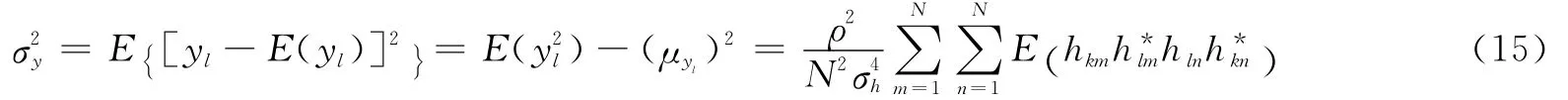
根据零均值随机变量的独立特性,式(15)求和符号后的求期望过程只在m=n时存在不为零的值,则有

令
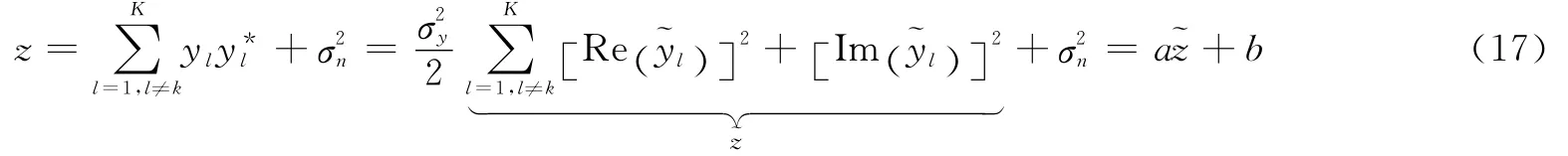

式中≥0。
结合式(8)与式(17),式(7)可简化为
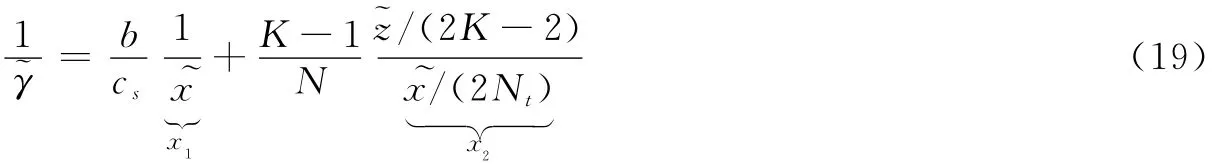
应用Jacobi变换,可由~x的PDF得到x1的PDF

式中x1≥0。
另一方面,随机变量x2服从第1自由度为2K-2,第2自由度为2N的F分布
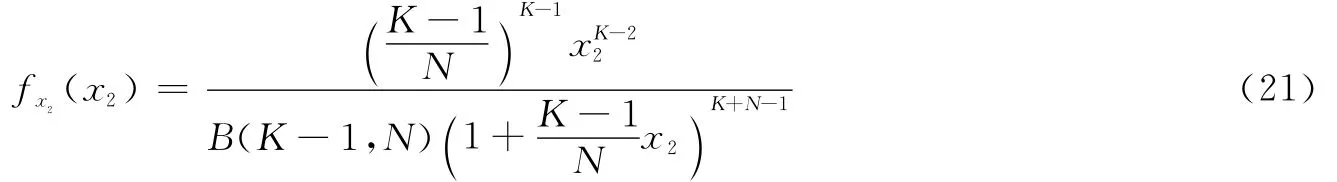
式中x2≥0,且
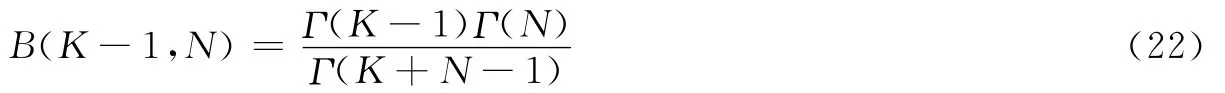
令

式中

则的累积分布函数为
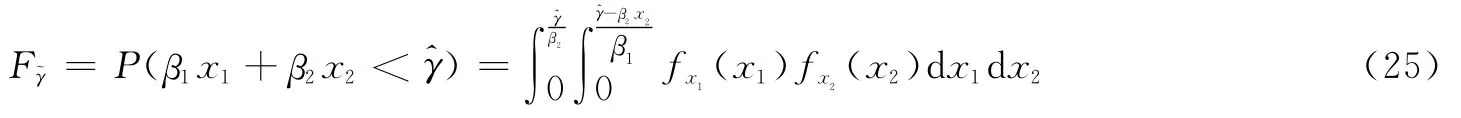
可得的PDF如下

考虑到是的倒数,根据式(26),可获得SINR的PDF为
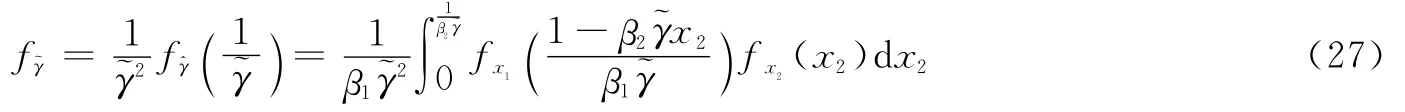
将式(20)与式(21,27)联合,有
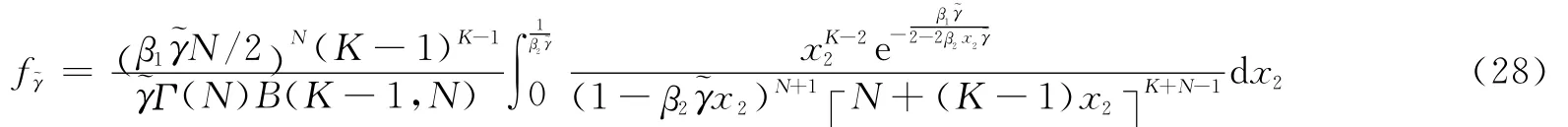
式中≥0。
至此完成了SINR的PDF推导过程。
3 仿真结果
为了验证本文推导的SINR的PDF公式的正确性,下面通过Matlab软件仿真产生充足的信道向量hk的随机样本,然后根据式(3)获得模拟的SINR值并利用 Matlab软件里的ksdensity()函数计算出SINR的PDF,并以此作为参考值和由本文推导的式(28)直接计算得到的SINR的PDF相比较。目前,3G与4G移动通信系统相邻蜂窝均采用频率复用因子为1的工作模式,由于相邻蜂窝同信道干扰的影响,实际系统的工作信噪比通常较低。因此,本文主要仿真低信噪比下SINR的PDF。
图1和图2分别给出了在不同典型信噪比和发射天线与用户数的情况下,推导的SINR和纯仿真的PDF曲线趋势图(其中,N=4K)。由图可知,在N=32、N=64时,本文推导得出的PDF和仿真模拟的PDF基本重合,尤其在低信噪比(SNR=-5dB)时,推导与纯仿真获得的PDF曲线几乎重合。
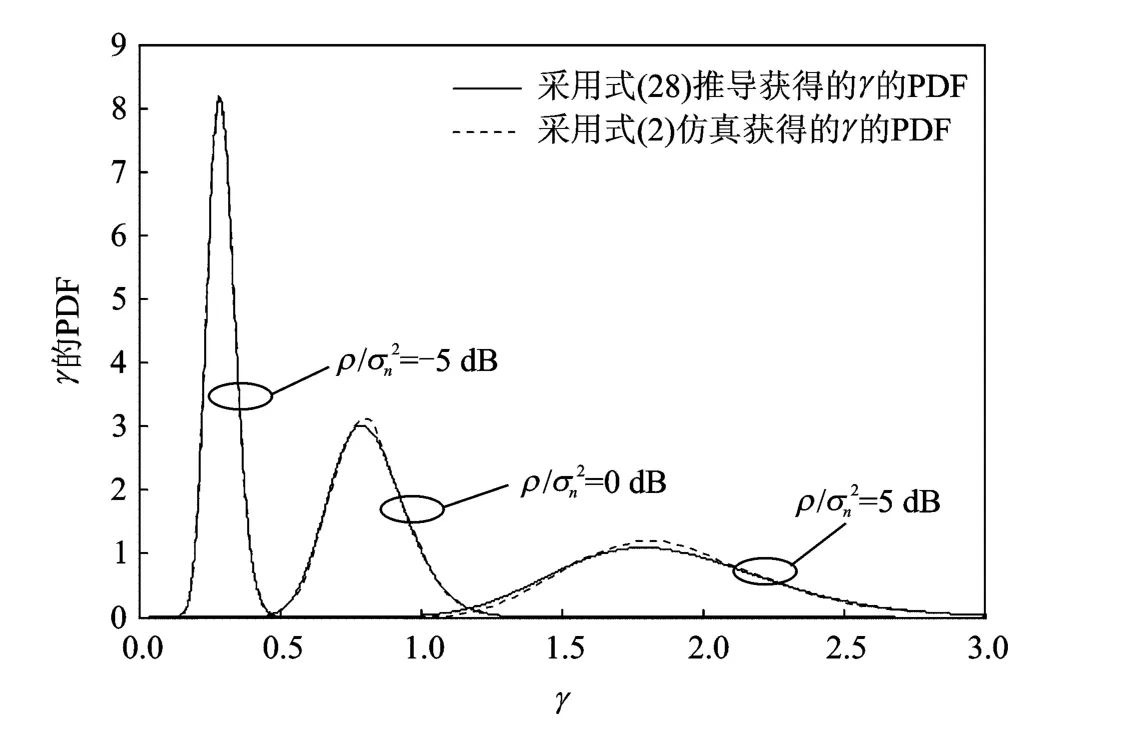
图1 固定用户数与基站发射天线数时,推导与仿真SINR的PDF曲线随信噪比变化的趋势图(N=32,K=8)Fig.1 Comparison between derived PDF of SINR and simulated PDF with fixed numbers of users and transmit antennas(N=32,K=8)

图2 固定用户数与基站发射天线数时,推导与仿真SINR的PDF曲线随信噪比变化的趋势图(N=64,K=16)Fig.2 Comparison between derived PDF of SINR and simulated PDF with fixed numbers of users and transmit antennas(N=64,K=16)

图3 固定用户数与信噪比时,推导与仿真的SINR的PDF曲线随基站发射天线数变化的趋势图(SNR=-5dB,K=8)Fig.3 Comparison between derived PDF of SINR and simulated PDF with fixed numbers of users and SNR(SNR=-5dB,K=8)
图3和图4给出了在固定用户数K=8时,不同信噪比,不同发射天线条件下的SINR的PDF曲线。同图1~2的结论类似,本文推导的概率密度函数在低信噪比下与实际概率密度曲线相差甚微,但在天线数较少且信噪比高于0dB时,由于对干扰部分概率分布的近似,使得推导的PDF同实际PDF曲线相比仍存在一定的改进空间,例如,在N=16,SNR=0dB时,仿真与推导得出的PDF曲线存在7%的峰值偏差。随着天线数增加,本文推导的公式与仿真的结果逐步趋于重合,最后收敛于同一曲线。另外,由图3与图4可知,随着信噪比的增加,基站配置越多发射天线,越能保证推导的公式与仿真结果接近重合。
4 结束语
本文推导了在中等规模MIMO系统下采用MF波束成形算法的SINR概率密度函数的表达式。通过仿真验证,该PDF在基站天线趋于大规模时逼近实际的概率分布。该结果为大规模MIMO通信系统平均误符号率、中断概率和平均速率和的推导与分析奠定了数学基础。

图4 固定用户数与信噪比时,推导与仿真的SINR的PDF曲线随基站发射天线数变化的趋势图(SNR=0dB,K=8)Fig.4 Comparison between derived PDF of SINR and simulated PDF with fixed numbers of users and SNR(SNR=0dB,K=8)
[1] Shu Feng,Wang Mao,Wang Yaxi,et al.An efficient power allocation scheme for leakage-based precoding in multi-cell multiuser MIMO downlink[J].IEEE Communications Letters,2011,15(10):1053-1055.
[2] Shu Feng,Wang Mao,Liu Tingting.Leakage-based precoding with power allocation for multi-cellular multiuser MIMO downlink[J].IET Electronics Letters,2010,46(24):1629-1630.
[3] 王大鸣,吕璐,窦冬冬,等.一种虚拟 MIMO中的低复杂度功率分配算法[J].数据采集与处理,2013,28(3):280-283.
Wang Daming,LüLu,Dou Dongdong,et al.Fast power allocation in virtual-MIMO systems[J].Journal of Data Acquisition and Processing,2013,28(3):280-283.
[4] Spencer Q H,Swindlehust A L,Haardt M.Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels[J].IEEE Transactions on Signal Processing,2004,52(2):461-471.
[5] Wiesel A,Yonina C E,Shlomo S.Zero-forcing precoding and generalized inverses[J].IEEE Transactions on Signal Processing,2008,56(9):4409-4418.
[6] Choi L U,Murch R D.A transmit preprocessing technique for multiuser MIMO systems using a decomposition approach[J].IEEE Transactions on Wireless Communication,2004,3(1):20-24.
[7] Sadek M,Tarighat A,Sayed A H.A leakage-based precoding scheme for downlink multi-user MIMO channels[J].IEEE Transactions on Wireless Communication,2007,6(5):1711-1721.
[8] Liu W,Yang L L,Hanzo L.SVD-assisted multiuser transmitter and multiuser detector design for MIMO systems[J].IEEE Transactions on Vehicle Technology,2009,58(2):1016-1021.
[9] Peel C B,Hochwald B M,Swindlehurst A L.A vector-perturbation technique for near-capacity multi-antenna multiuser communication-part I:channel inversion and regularization[J].IEEE Transactions on Communication,2005,53(1):195-202.
[10]Hakjea S,Sang-Rim L,Inkyu L.Generalized channel inversion methods for multiuser MIMO systems[J].IEEE Transactions on Communication,2009,57(11):3489-3499.
[11]卢敏,酆广增,孟庆民.多用户 MIMO系统低复杂度收发联合波束成形方案[J].数据采集与处理,2012,27(4):417-421.
Lu Min,Feng Guangzeng,Meng Qingmin.Joint beamforming scheme with low complexity for multiuser MIMO system[J].Journal of Data Acquisition and Processing,2012,27(4):417-421.
[12]Rusek F,Persson D,Buon Kiong Lau,et al.Scaling up MIMO:Opportunities and challenges with very large arrays[J].IEEE Signal Process Magazine,2013,30(1):40-60.
[13]Thomas L M.Non-cooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communication,2010,9(11):3590-3600.
[14]Erik G L,Fredrik T,Ove E,et al.Massive MIMO for next generation wireless systems[J].IEEE Communication Magazine,2014,52(2):186-195.
[15]Chan-Sic P,Yong-Suk B,Aman M B,et al.Complexity reduced zero-forcing beamforming in massive MIMO systems[C]∥International Theory and Application Workshop,2014.San Diego,CA:IEEE,2014:1-5.
[16]Kammoun A,Muller A,Bjornson E,et al.Linear precoding based on polynomial expansion:Large-scale multi-cell MIMO systems[J].IEEE Journal of Selected Topics in Signal Processing,2014,8(5):861-875.
[17]Zhang W,Pan C,Du B,et al.Downlink SINR study in multiuser large scale antenna systems[J].Wireless Personal Communications,2014,79(2):1539-1556.

