改进的容积卡尔曼滤波（CKF）算法在短期负荷预测中的应用

吉博文 邹红波 何 平 倪 浩 祝 迪

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2宜昌供电公司，湖北 宜昌 443002）

负荷预测是现代电力科学研究的重要领域之一，它对电力系统的安全经济运行及国民经济都有非常重要的意义.随着我国电力事业的发展，国家和电力部门对电网管理的质量要求越来越高，使得如何提高短期电力负荷预测精度的问题得到广泛研究［1－6］.

卡尔曼滤波算法是一种递推滤波方法，主要优点是能充分利用待测数据过程的相关信息.该方法应用于负荷预测的具体过程是：把负荷分为确定性分量和随机性分量，对确定分量通常采用线性回归模型预测，对随机分量则采用卡尔曼滤波算法预测.但当随机变量为强非线性随机变量时，滤波则难以取得较高的精度.20世纪90年代出现了较新的非线性滤波方法，这类方法采用样本加权求和直接逼近随机函数，且其测量更新部分采用卡尔曼滤波的更新原理，这类滤波器有无迹卡尔曼滤波器、中心差分卡尔曼滤波器、容积卡尔曼滤波器等［7－8］.本文工作是在电力系统负荷随机变量存在较强非线性的情况下，将所有引起负荷变化的因素如降雨、温度、湿度等归结为针对随机系统的随机因素输入，采用基于改进容积卡尔曼滤波（CKF）算法进行预测，并以仿真测试验证了该模型的有效性.

1 卡尔曼滤波算法

随机信号及其测量过程的数学模型分别为：

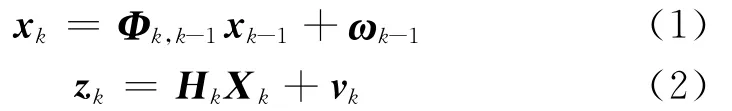
基于投影法推导的卡尔曼滤波器递推公式和预测方程为：

状态预测方程：

误差协方差预测：

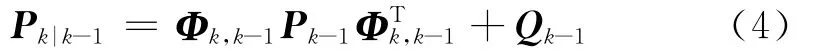
状态估计校正：

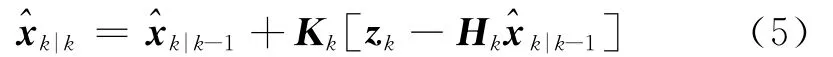
误差协方差估计校正：

卡尔曼增益：

以上各式中，xk是n维状态向量；zk是m维观测向量；Φk，k－1是n×n维一步状态转移矩阵；Hk是m×n维观测矩阵.n维系统噪声ωk和m维观测噪声vk均是互不相关的零均值高斯白噪声序列，并且具有如下的统计特性：

通常情况下，滤波初始值0＝0，P0＝I，0和I均是相应维数的零矩阵和单位矩阵.

2 CKF算法

假定有如下离散非线性系统

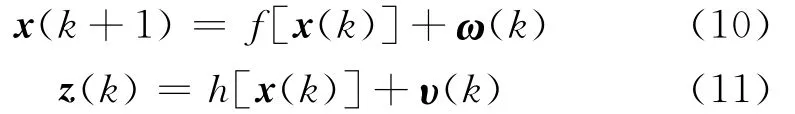
式中，x（k）为状态向量，f（·）为非线性系统状态函数，ω（k）为系统的过程噪声，且为零均值高斯白噪声，满足分布ω（k）～N｛0，Q（k）｝；z（k）为测量值，h（·）为非线性观测函数，v（k）为系统的量测噪声，满足分布v（k）～N｛0，R（k）｝；状态的初始值x（0）满足分布x（0）～N｛0，P（0）｝.

1）容积点选取

为了解决高斯密度函数与多变量非线性函数乘积的积分，Arasaratnam等人采用了三阶容积积分方法，用容积点加权求和取代了加权高斯积分计算，如对于函数f（x）的加权高斯积分，有

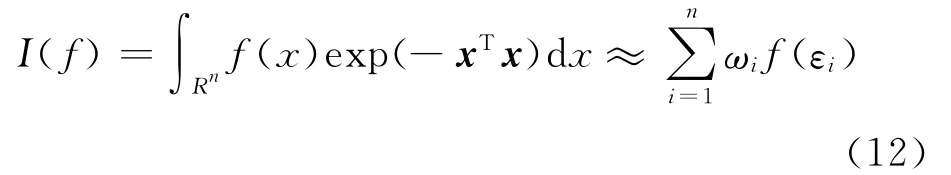
式中，f（x）是任意函数，Rn是积分区域，容积点εi为：

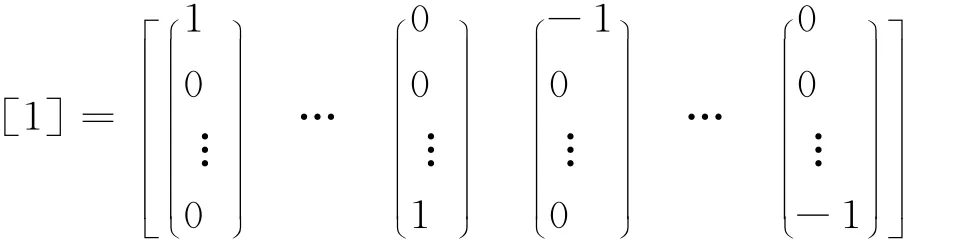
式中，［1］i表示［1］的第i列，［1］为：

2）时间预测

计算容积点：

传播容积点：

估计预测均值：

估计预测协方差：

3）量测更新

当获得时间预测值后，利用下面一组递推方程对状态和方差进行更新.CKF算法量测更新方程如下：

计算容积点：

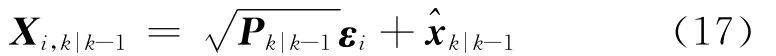
传播容积点：

计算新息方差和协方差矩阵：

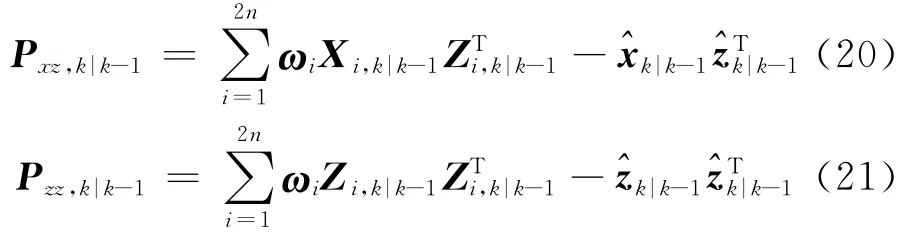
计算滤波增益矩阵：

计算量测更新方程：

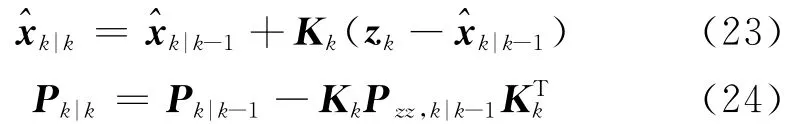
3 卡尔曼滤波负荷预测模型参数辨识

3.1 模型阶数辨识

本文采用Hankel矩阵法辨识模型的阶，在系统的随机负荷序列x1，x2，…，xN已知的情况下，按以下形式构造Hankel矩阵（简称为H矩阵）.

其维数为l×l，由于观测信息中总会有噪声，要有效地估计含噪声系统的阶数，可以采用如下算法：

1）弱噪声系统条件下

计算每个l值（l＝1，2，3，…）时，k取不同值时H阵行列式的平均值.令

当Dl达到极大值时，即为系统的估计阶数n.

2）强噪声系统条件下

如果负荷序列所含噪声比较大，为了可靠地确定模型的阶数，构造Hankel矩阵时，不能直接用随机负荷序列，而采用随机负荷序列的自相关系数构造H阵.用自相关系数代替H阵中的元素，构成以自相关系数ri为元素的H阵，再计算l取不同值时H阵的行阵式值，比较所得行阵式值，达到极小值时，l值即为所求系统的阶数.

3.2 噪声协方差Q及R初始值的辨识

关于Q（t）的选取方法，对通常的动态系统，可认为滤波误差的统计特性基本保持不变，近似为正态分布白噪声，因此，可取Q（t）为常值Q，而Q通过事先的模拟计算加以确定.当采用模拟观测量进行计算时，主要考虑的是滤波误差序列，开始时若Q选取过小，则滤波误差序列将发散；Q增大到某个值Q＊时，滤波误差的趋势将会在某一稳态值附近摆动，此时有最小的稳态误差；若Q超过Q＊，滤波误差的变化趋势仍会在某一稳态值附近摆动，但稳态误差将随Q增大，因此Q较好的取值应该是稍大于Q＊.当用实际负荷值进行计算时，主要考察的是预测残差序列.对于某些情况，滤波误差的统计特性随时间变化较大，此时Q（t）取常值未必恰当，应该是随时间变化的，这应根据具体问题而定.R（t）的选取方法与Q（t）类似.

4 改进方法及应用

通过不断更新状态转移矩阵，可得到改进的容积卡尔曼滤波方法，具体计算步骤为：

1）导入随机负荷SJ，计算初始参数φ（0）、C、Q、R.C为容积点，其个数是模型阶数的2倍.

2）设置初始条件：初始迭代值（0），初始值方差P（0）.

3）时间更新：根据式（13）计算容积点，式（14）计算传播容积点，式（15）估计预测均值（k｜k－1），式（16）估计预测协方差P（k｜k－1）.

4）状态测量更新：根据式（17）计算容积点，式（18）和式（19）计算传播容积点Zi，k｜k－1和｜k－1，式（20）和式（21）计算新息方差阵Pxz，k｜k－1和协方差阵Pzz，k｜k－1；根据式（22）计算滤波增益矩阵Kk，根据式（23）计算状态值｜k－1，根据式（24）计算状态值方差Pk｜k.

5）更新状态转移矩阵：删除导入的随机负荷数据SJ的第一个数据，余下数据依次左移，左后一个数据用（k）替换，获得新的数据序列SJ（k）.根据新的数据序列计算φ（k），重复3）、4）过程.具体仿真流程如图1所示.

图1 改进的容积卡尔曼滤波仿真流程图

为了验证改进算法的有效性，用2011年某地8月的22d数据建立模型，对该月余下9个工作日216个时刻的负荷进行预测.样本负荷分析过程为：处理异常数据点；采用去均值的方法处理样本负荷；抽取样本随机负荷，确定随机负荷为强噪声负荷；运用基于自相关函数的Hankel矩阵法辨识得模型为4阶模型，并利用Yule－Walker方程求取最佳阶数下状态转移矩阵以及其它模型系数.模型参数以及递推初始值如下：状态转移矩阵A＝［0.395 10 －0.628 14 0.118 25 0.539 07 －1.019 94 ；1 0 0 0 0；0 1 0 0 0；0 0 1 0 0；0 0 0 1 0］；量测噪声协方差初始值：R＝120；状态噪声协方差初始值：Q＝［198 0 0 0；0 200 0 0；0 0 199.6 0；0 0 0 119.67］；系统阶数n＝4；递推初始值（0）＝0.01＊randn（n，m），P（0）＝eye（n）.

模型值与真实值对比如图2所示，可以看出改进容积卡尔曼滤波器模型始终处于稳定状态，预测误差较小.由具体数据可以算出预测阶段9d平均相对误差为0.16%，平均绝对百分误差2.76%，小于3%，说明其预测精度达到预期效果，令人满意.

图2 负荷预测和实测值对比

为了更清楚地显示预测效果，现从预测数据库中随机抽取1d的负荷预测数据（随机抽取为第3d），并与实际负荷数据进行对比，结果见表1.

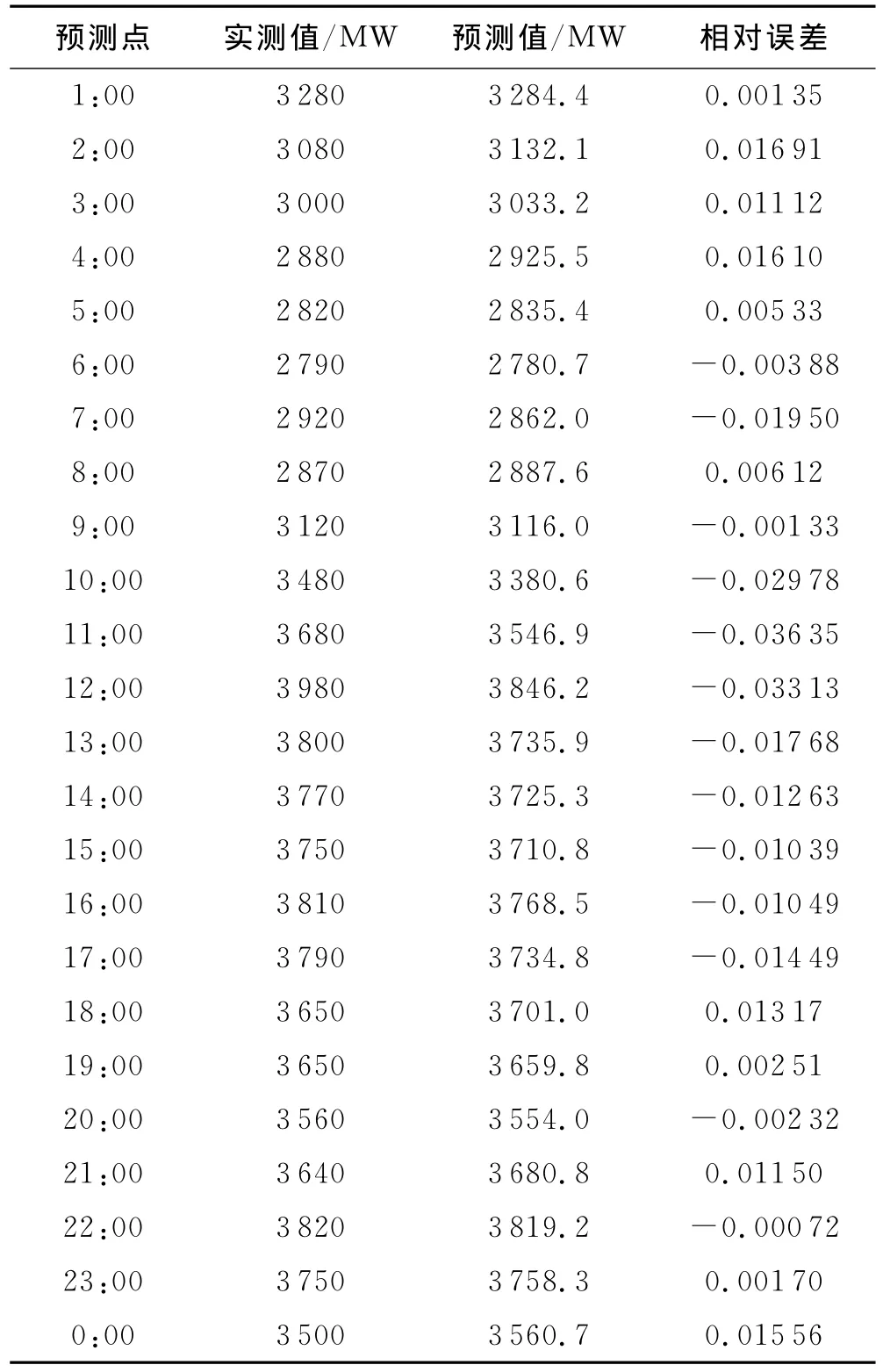
表1 第3d预测结果比较

5 结 语

本文用改进CKF对电力系统负荷建模预测，将所有引起负荷变化的因素如降雨、温度和湿度等归为随机系统中的随机因素来计算，模型结果证明了这种方法是有效的，具有较高的计算精度.

CKF方法用容积点对非线性序列的近似，避免了对非线性函数的解析求导（还可以处理不可导的非线性函数），减少了计算量，节省了计算时间.

本文的噪声协方差Q及R均是定常值，此方法要求对噪声统计特性的先验知识有准确的掌握，如果采用了不准确的噪声统计特性设计滤波器模型，就会产生较大的估计误差，甚至导致滤波发散.解决该问题可以借鉴自适应卡尔曼滤波，通过引入噪声估值器在线校正模型参数或噪声统计值，提高滤波精度.实际应用中对此问题可做进一步研究.

［1］ 孟思齐，杨洪耕.基于卡尔曼滤波二次修正的短期负荷预测［J］.电网与水力发电进展，2008，24（2）：78－82.

［2］ 马静波，杨洪耕.自适应卡尔曼滤波在电力系统短期负荷预测中的应用［J］.电网技术，2005，29（1）：75－79.

［3］ 张 民，鲍 海，晏 玲，等.基于卡尔曼滤波的短期负荷预测方法的研究［J］.电网技术，2003，27（10）：39－42.

［4］ 廖旎焕，胡智宏，马莹莹，等.电力系统短期负荷预测综述［J］.电力系统保护与控制，2011，39（1）：147－152.

［5］ Al－Hamadi H M，Soliman S A.Short－term Electric Load Forecasting Based on Kalman Filtering Algorithm with Moving Windows Weather and Load Model［J］.Electric Power System Research，2004（68）：47－59.

［6］ 吉培荣，简作群.电力系统短期负荷预报［J］.水电能源科学，1997，15（2）：37－41.

［7］ 刘 胜，张红梅.最优估计理论［M］.北京：科学出版社，2011.

［8］ 王志贤.最优状态估计与系统辨识［M］.西安：西北工业大学出版社，2004.