基于改进型混合蛙跳算法的支持回归机大坝变形预测模型

卢远富 包腾飞 李涧鸣 孙鹏明 王 甜

（1.河海大学 水利水电学院，南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098；3.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098）

大坝变形是较直观且可靠地反映大坝安全的监测量之一，对其进行分析预测是监控大坝运行安全的重要内容［1］.到目前为止，主要有支持向量机（SVM）模型、统计模型、神经网络模型等应用于大坝变形预测［2］.统计模型为传统预测模型，其具有简单直观的优点，但预测精度易受预报因子间的相关性影响，且其泛化能力较差；神经网络模型有较强的非线性逼近能力，但在其应用于大坝变形拟合及预测时仍然易出现收敛较慢以及过拟合的问题［3］；SVM模型在处理高维数以及非线性的问题时具有较好的泛化能力，但该模型参数的选取对模型的精度会产生很大的影响，且目前参数选取尚无统一最好的优选方法.在SVM模型的基础上引入ε不敏感损失函数从而得到支持回归机（SVR）.SVR可以用于解决大坝变形回归、拟合等问题，且SVR继承SVM的优点，其稳定性和泛化能力均较高.SVR模型的预测精度的影响因素主要有惩罚参数c和核函数参数.因此针对目前对于SVR的参数优选问题，本文采用一种基于拉丁超立方体抽样（LHS）和自适应移动算子的改进型混合蛙跳算法（ISLFA）对SVR模型进行参数寻优来提高其预测精度.通过实际工程算例验证，基于LHS和自适应移动算子的改进型混合蛙跳算法的SVR模型能有效增强全局寻优能力，且拟合精度和预测精度均取得较好的结果.

1 改进型的混合蛙跳算法

1.1 混合蛙跳算法

Eusuff和Lansey2003年在研究管网优化设计问题时提出了混合蛙跳算法，该算法是一种新的仿生优化算法［4］.该算法模拟现实青蛙觅食的过程，首先将所有青蛙分成多个小组，每个小组内进行局部寻优；之后的全局搜索再采用模因进化算法的方法进行周期性的混合和重组，达到种群信息能够在全局和局部进行深度交换.这种深度局部搜索和全局信息交换相结合的策略能够保证算法更大程度地落入局部最优值，从而向全局最优靠拢［5］.混合蛙跳算法的算法流程可以参见文献［6］.

1.2 改进的混合蛙跳算法

混合蛙跳算法属于一种随机优化算法，故存在有限数量的初始化种群的均匀性较差，移动步长随机性较大等问题，这些问题将对算法的收敛性和求解精度产生一定程度的影响［7］.本文尝试针对这两方面的问题做出一定的改进.

1.2.1 利用改进的LHS进行青蛙种群初始化

混合蛙跳算法中种群初始化是其重要一步，均匀性较好的初始种群可以有效加快收敛，加快全局寻优.利用试验设计领域的一种常用方法—拉丁超立方体抽样方法（LHS）来对蛙跳算法种群初始化，得到种群均匀性良好的青蛙种群，加快后期全局寻优及种群收敛性.

利用LHS初始化的蛙跳种群可用矩阵X表示：

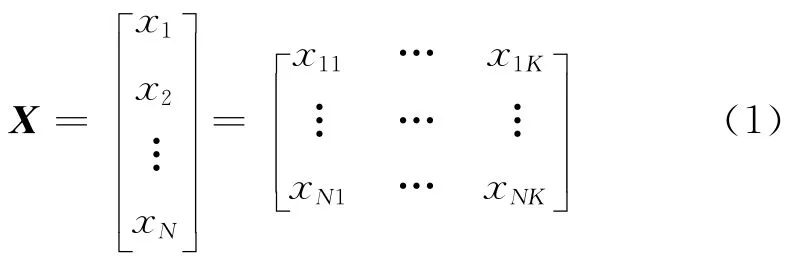
式中N表示抽样点数，K表示试验次数，即xNK代表第N只青蛙第K维的值.原始的LHS的样本方差较小，但是由于给出的试验点是随机的，故其提供的试验设计中有一部分较好，也有相当一部分不尽如人意，为保证LHS的稳定性，采用极大极小值距离准则对LHS进行筛选以达到改进的目的［8］.

如果试验设计中的一组抽样可以将任意试验点之间的最小距离最大化，则该抽样称为最大化最小距离设计，即：

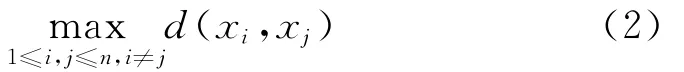
其中，d（xi，xj）表示任意两个试验点xi，xj之间的距离

其中，m表示试验点的两两组合个数，也即m＝n（n＋1）／2，通常t＝1或者t＝2表示任意两点间的欧式距离测度.

1.2.2 自适应移动算子

针对SFLA的解更新大小和方向随机性强的问题，本文设计一种线性自适应移动算子来进行改进：

其中，t表示模因组的当前进化代数，N表示模因组的最大进化代数.由式（4）可以得出，移动算子随着种群进化而逐步增大，其变化序列为［1／N，2／N，…，1］.改进之后的线性自适应移动算子在种群进化前期的值较小，使得种群进化前期模因组内的移动步长不至于过大，即能对种群前期进化的全局搜索进行一定的抑制，并较好扩大种群的寻优范围，当种群进化至中后期，移动算子的值较大，解的寻优过程能保持较好的全局搜索能力，收敛速度得以加快［9］.故将经典的随机移动算子改进为线性移动算子能使该算法具有更佳的全局寻优能力.

此外参数寻优中设置合适的最大步长可以均衡局部搜索和全部搜索，对于每一维寻优参数的取值范围可能不一致，因此每维参数的步长设置不一样.

2 支持回归机（SVR）

2.1 SVR原理

在支持向量机（SVM）的基础上引入不敏感函数，得到不敏感函数支持回归机（ε－SVR）.SVR 和SVM的基本思想均是寻找一个最优分类面，但SVM是寻找一个最优分类面使得两类样本分开，而SVR是寻找一个最优分类面使得所有训练样本离最优分类面的误差最小.

不失一般性，设含有l个训练样本的训练集｛（xi，zi），…，（xl，zl）｝，其中特征向量xi∈Rn，为第i个训练样本的列向量，目标输出值zi∈R1（i＝1，2，…，l）.通过寻求适当的映射f（x），将原低维问题通过“升维”的方法转换至高维空间并在高维空间中构造出符合一定要求的最优线性拟合函数，具体来讲就是通过引入不敏感损失函数使其对于所有训练样本都可以在精度ε下用f（x）进行拟合.

定义ε线性不敏感函数：

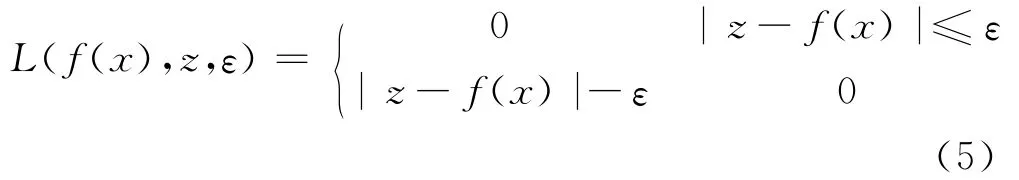
其中，f（x）为回归函数返回的预测值；z为对应的真实值.

类似于SVM分类情况，考虑允许拟合误差的情况所引入的松弛因子ξi≥0，ξ＊i≥0，支持向量回归机（SVR）的标准形式如下

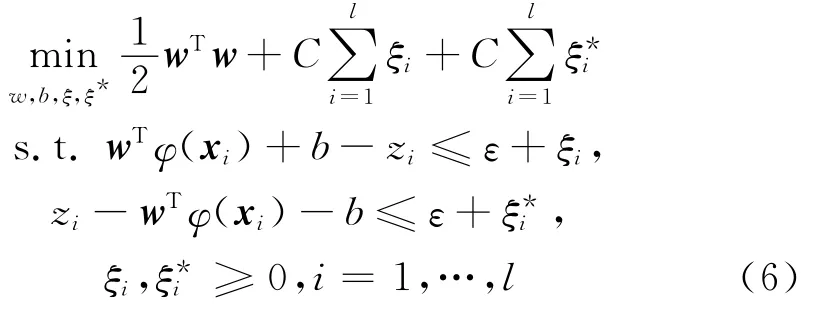
式中，w为权向量，b为偏差值；ε为训练样本的拟合的误差精度，即｜｜≤ε（i＝1，…，l）；C为惩罚参数，且C＞0.

引入Lagrange函数可得对应的对偶问题：

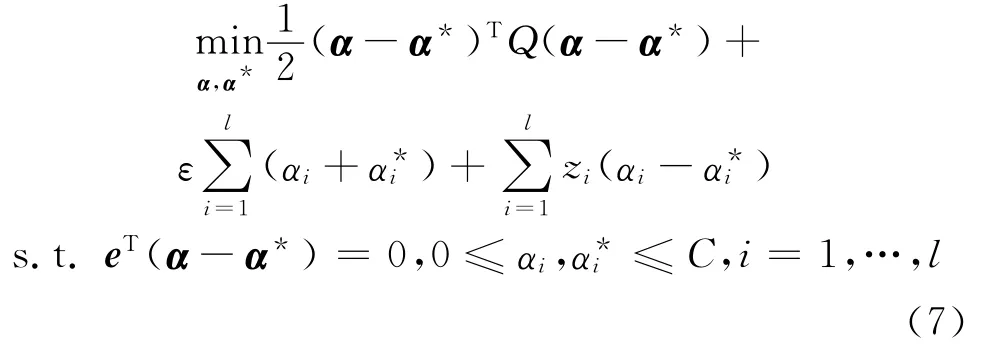
式中，αi为l维支持向量机，Qij＝K（xi，xj）≡φ（xi）Tφ（xj）为核函数.求解式（7），得到拟合函数为

式中，K（xi，xj）≡φ（xi）Tφ（xj）为核函数.

本文核函数选用较为常用的RBF核函数，其形式如下：

以上求解过程通过将原问题转化为对偶问题来化解“维数灾难”，也即求解规模与输入空间的维数无关，再经过处理得到原问题的解.

2.2 SVR参数

对于SVR模型的核函数取为RBF核函数时，影响SVR模型精度的参数主要为两个：惩罚参数C和核参数σ.RBF核函数的核参数σ为核宽度，其代表着样本数据在高维特征空间中分布的复杂程度，因此参数σ与输入数据（即训练的学习样本）本身的输入空间有关.当样本越大，参数σ的取值应当越大；样本空间越小，参数σ的取值应当越小.惩罚参数C的作用是控制模型复杂度与逼近误差的折中，C的取值越大，则表明对数据的拟合程度越高，相应的复杂度及其学习成本也就越高，易导致“过学习”的现象，模型的泛化能力降低，当C的取值若过小，虽然会极大地简化计算复杂度，但却会带来拟合误差较大，进而出现“欠学习”的问题，同样也会出现泛化能力降低［10］.

在SVR模型中，参数C和σ的选取会对回归拟合产生极大的影响，故SVR的参数优选一直都是广为关注且具有重要意义的问题.目前常用的优化方法有：网格搜索法等确定性算法以及以遗传算法（GA）、粒子群算法（PSO）和蛙跳算法（SFLA）等群智能算法.在实际应用中，参数C和σ的实际选取值不可能达到绝对最优，本文中利用参数优选之后的SVR模型的拟合与预测误差的大小来反映参数选取误差的大小.

3 建立ISFLA－SVR的大坝变形预测模型

利用改进型的混合蛙跳算法（ISFLA）对SVR模型的参数C和σ进行寻优，考虑到核参数σ敏感性较高，模型中采用g＝1／2σ2进行寻优，进而得到最佳的ISFLA－SVR大坝变形预测模型.适应度函数采用训练集交叉验证（CV）意义下的均方差作为ISFLA的适应度函数值.因此ISFLA－SVR大坝变形预测模型的流程图如图1所示.

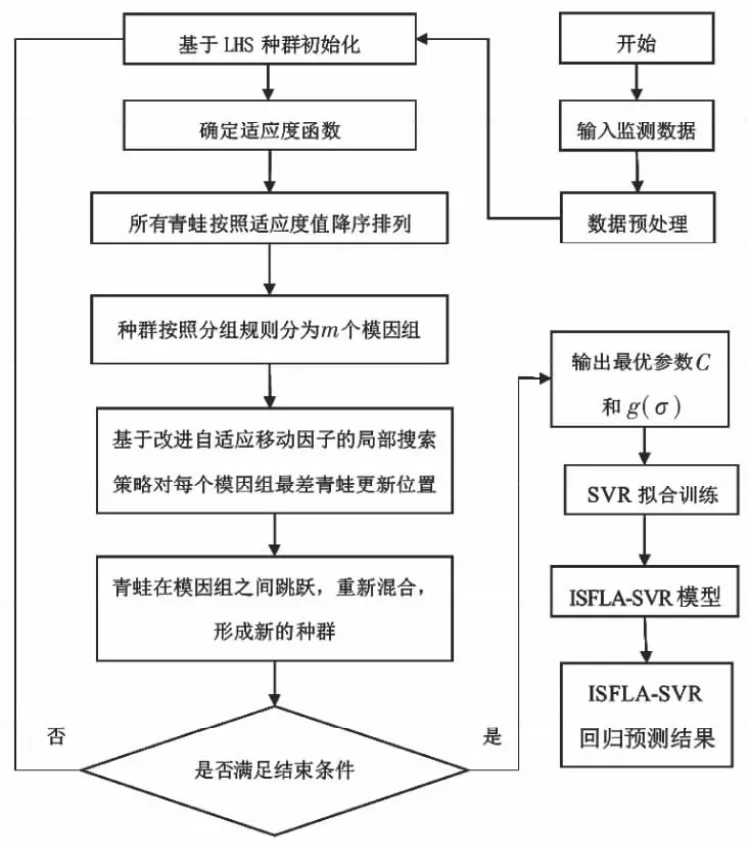
图1 ISFLA－SVR模型流程图

4 工程算例

以某混凝土双曲拱坝为例，该坝坝顶高程1 245 m，最大坝高为294.5m.该坝采用正垂线对大坝变形进行监测，考虑监测时间较长并且间隔很近，容易造成监测数值过于接近，因此模型计算中每间隔7天（即一周）选一组数据进行计算，本文的模型数据拟合时段：20100701至20121220共130组实测值，模型预测时段：20121227至20130228共10组观测值.

为加快学习速度，消除由于量纲不同所引起的的变异信息，使得分析结果更加合理，需要对样本数据进行预处理［11］，本文采用归一化至［0，1］区间：

式中，Xmin和Xmin分别为每组样本数据的最大值和最小值.

初始化种群参数设置：种群规模设为150个，子种群设为15个，子种群内更新代数设为15次，种群最大进化代数为20，惩罚因子c取值范围设为［10，100］，其最大移动步长设为10，g的取值范围设为［0.01，10］，其最大移动步长设置为1.通过ISFLASVR模型进行寻优参数.经过ISFLA进行参数寻优，得到参数c＝63.755 9，g＝0.083 2，通过进一步转换可以得到惩罚因子c＝63.755 9，核参数σ＝2.451 5.

为了检验ISFLA－SVR模型拟合精度和预测精度，本文建立3种模型：ISFLA－SVR 模型、SFLASVR模型以及传统的多元回归模型，利用这3种模型对本工程算例数据进行拟合和预测并作结果对比分析.通过进一步绘制拟合比较图与预测比较图，可以更加直观地了解各模型的拟合精度与预测精度.

拟合对比图如图2所示，从图2可以看出ISFLA－SVR模型的拟合精度很高，在一些数据变化的波动处也能很好地拟合，而多元回归模型与实测值偏离较大.3种模型，即ISFLA－SVR模型与SFLA－SVR以及多元回归模型的预测对比图如图3，从图3中易得出ISFLA－SVR模型的预测精度比其他两种模型要高.

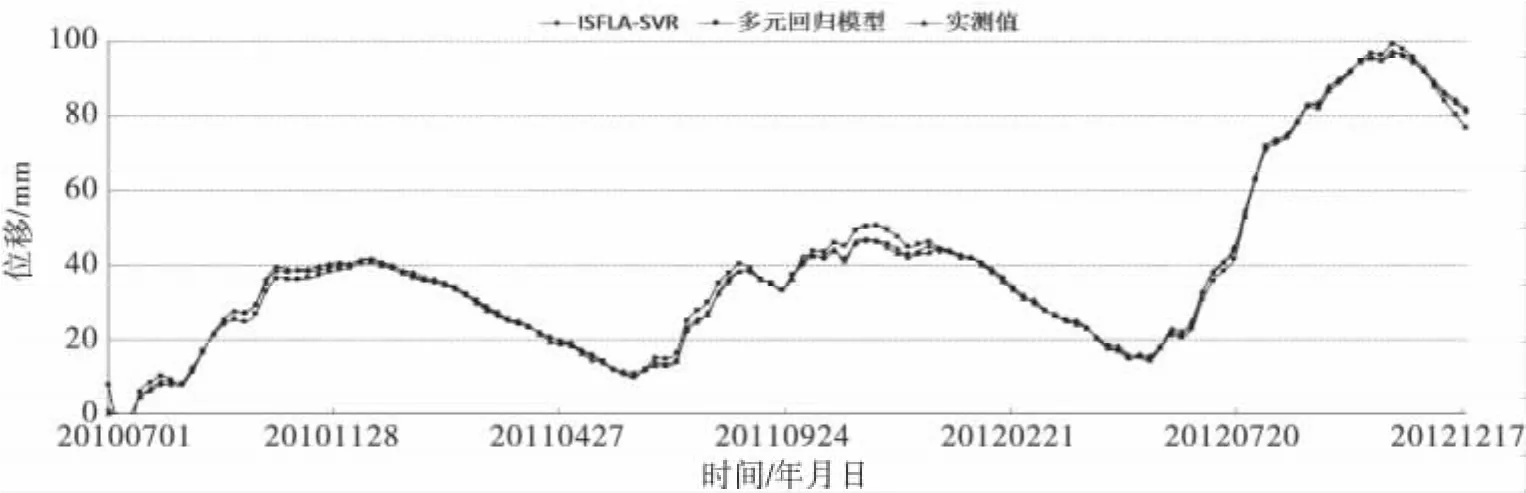
图2 不同模型拟合图

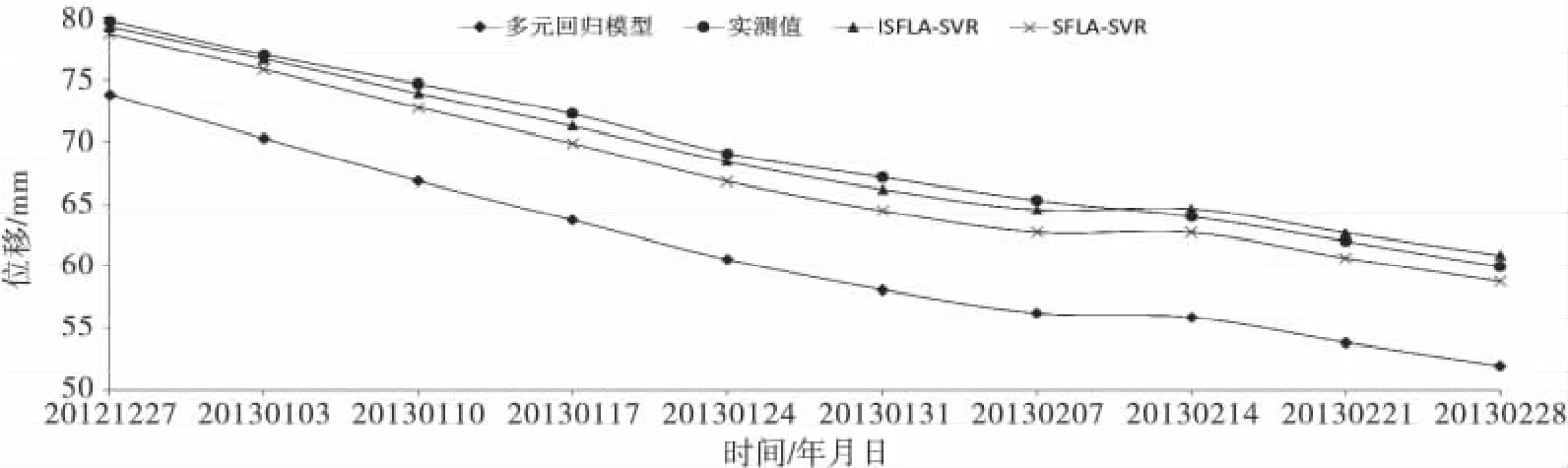
图3 不同模型预测曲线图

为了对3种模型拟合精度与预测能力进行定量评价，采用均方差FMSE这一指标来进行比较和评价：

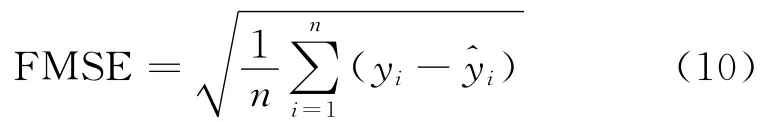
式中，n为样本数，yi为监测真实值为模型计算值.

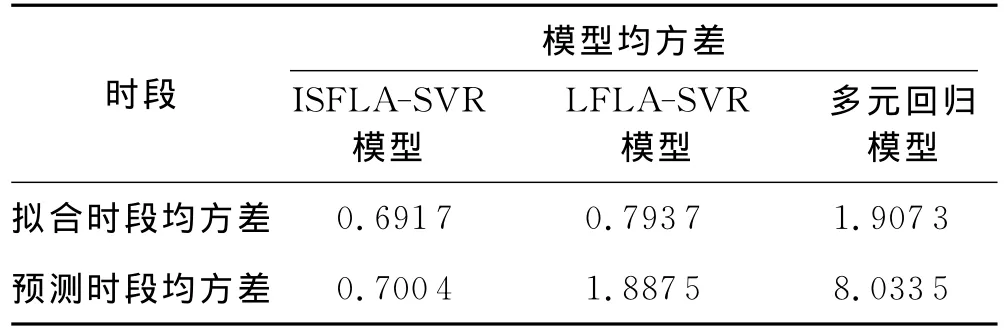
表1 3种不同模型的均方差比较

由上表可以得到，3种模型中拟合精度ISFLASVR模型最高，然后依次是SFLA－SVR模型和多元回归模型.就3种模型的预测精度而言，ISFLA－SVR模型的预测精度最高，均方差仅0.700 4mm，较SFLA－SVR模 型 的 预 测 精 度1.887 5mm 提 高 了62.89%，这也反映了ISFLA－SVR模型的参数选取的误差较SFLA－SVR模型明显减小；多元回归模型的均方差为8.033 5mm，与实测值偏离很大，预测精度最差，同时这也与图3的结果吻合.

5 结 论

本文利用SVR模型对大坝变形进行预测，并引入混合蛙跳算法对SVR模型参数进行优化.利用拉丁超立方试验初始化青蛙种群和采用自适应移动算子对混合蛙跳算法进行改进，使得参数寻优过程中均衡局部最优与全局最优，即陷入局部最优的情况能得到更大程度的避免.通过以上实际工程算例的分析计算可以得出：

1）ISFLA－SVR模型可以用于大坝变形预测，并且精度很高.同传统多元模型相比，ISFLA－SVR模型具有更高的拟合精度和更强的预测能力，同ISFLASVR模型相比，SFLA－SVR模型的拟合精度和预测能力均有一定程度的提高.

2）本文中初步将ISFLA－SVR模型参数优选的误差大小通过模型拟合预测均方差的大小来反映，参数误差的具体真实大小及范围控制仍需要进一步研究.

3）基于LHS能够得到均匀性较好的初始化种群，从而自适应移动算子可以使得SVR模型参数寻优能够有效跳出局部最优，并同时保持种群多样性.

［1］ 李守巨，刘迎曦，刘玉静.基于进化神经网络混凝土大坝变形预测［J］.岩土力学，2003，24（4）：635－639.

［2］ 范振东，崔伟杰，郭芝韵，等.基于改进的PSO－SVM法的大坝安全非线性预警模型研究［J］.水电能源科学，2014，32（11）：72－75.

［3］ 屠立峰，包腾飞，唐 琪，等.基于SCDS－SVM的大坝安全监测模型［J］.三峡大学学报：自然科学版，2015，37（2）：6－9.

［4］ EuSuff M M，Lindsey K E.Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm［J］.Journal of Water Source Planning and Management，2003（3）：210－215.

［5］ 李建军，郁 滨，陈武平.混合蛙跳算法的改进与仿真［J］.系统仿真学报，2014，26（4）：755－760.

［6］ 王怡然，王联国.改进的混合蛙跳算法确定河流水质模型参数［J］.甘肃农业大学学报，2014（2）：155－159.

［7］ 苏 仟.混合蛙跳算法研究与改进［D］.西安：西安电子科技大学，2014.

［8］ 刘新亮，郭 波.基于改进ESE算法的多目标优化试验设计方法［J］.系统工程与电子技术，2010，32（2）：410－414.

［9］ 马平莉.混合蛙跳算法研究［D］.西安：西安电子科技大学，2013.

［10］宋晓华，杨尚东，刘 达.基于蛙跳算法的改进支持向量机预测方法及应用 ［J］.中南大学学报：自然科学版，2011，42（9）：2737－2740.

［11］王 泉，郑东健，范振东，等.基于PCA－SVR模型的大坝裂缝早期预报研究［J］.人民长江，2015，46（5）：35－38.