太平哨电站泄洪坝弧形闸门振动试验研究
赵振华 张宇飞 王山山
(河海大学 力学与材料学院,南京 210098)
随着生产力的发展和人们需求的不断增加,越来越多的闸门被用于水利工程当中.由于弧形闸门不设门槽,启闭力较小,运转可靠、水力学条件好并且能满足各种类型泄水孔道需要的优点[1].弧形钢闸门已经成为水工建筑物中运用最为广泛的一种门型.纵观国内外水利枢纽中弧形闸门实际运行中的情况,闸门在启闭过程中或局部开启时,都可能发生振动[2].引起闸门振动的原因来自许多方面,情况比较复杂.但综合国内外许多专家的研究认为,闸门在启闭运行中的振动都是由于动水作用的不平稳所引起的[3-4].黄廷璞等[5]通过对我国20多座弧形闸门破坏事故的调查研究中发现失事闸门均是在明显的振动荷载作用下引起闸门发生强烈的振动,从而造成弧形闸门支臂动力失稳而导致闸门破坏.因此,闸门在运行过程中的振动问题是水利工程中一个非常重要的研究课题[6].
引起每个闸门振动的外因虽有不同解释[7],诸如闸门开度、后门淹没水跃、止水漏水、闸门低缘型式等.但是引起闸门振动的内因都与闸门结构的自振频率有关.闸门的自振频率是闸门结构的固有属性,与闸门结构的刚度、质量分布和材料属性有关.并且闸门振动的大小取决于闸门结构的自振频率与激励频率的关系以及结构的刚度与阻尼.当作用力的激励频率接近或等于闸门的自振频率时,闸门就会发生共振,从而使闸门受到损害.虽然关于闸门振动的研究有多种方法,但由于诸多方面的原因现场原型试验仍是研究闸门振动的重要方法[8].因此,为了确保闸门在运行中的安全性,必须定期组织对闸门进行全面深入的振动试验研究.
1 工程概况及试验方案
1.1 工程概况
太平哨水电站地处辽宁省丹东市宽甸满族自治县东部山区.电站为混合式开发,水力枢纽由主坝、副坝、引水道和厂房等建筑物组成,水电站为二等工程,大坝为2级建筑物.大坝为混凝土重力坝,坝顶高程196.0m,坝顶全长555.6m,最大坝高44.0m,顶宽8.0m,共36个坝段.主坝在3号-23号坝段设有开敞式溢流口,布置20个工作门,门型为弧门,堰顶高程181.5m,孔口尺寸为12m×10.5m.为高孔泄洪,最大泄流量为18 600m3/s,挑流、面流消能方式.闸门全局现场情况如图1所示.

图1 闸门现场图
1.2 振动试验方案
由于太平哨电站泄洪坝的20孔弧形闸门,其尺寸、材料均相同,并且避免20个闸门全部进行振动试验对水量损失过大.本次仅选取了两个典型的闸门进行振动试验,坝中10号孔弧形闸门和平常开启噪声较大的17号孔弧形闸门进行振动试验研究.分别对这两个闸门进行了结构的动力特性试验(自振频率、阻尼)和闸门启闭过程中的动力响应(加速度)试验.
试验中在每个测点布置一枚CL-YD-103型压电式加速度传感器来测量布置点的加速度,经由DH5857-1电荷适调器连接到DHDAS5920动态信号采集仪,并由计算机来控制和数据保存.此外,在用瞬态激励法做闸门动力特性试验时,还采用了安装有力传感器的激励力锤.10号和17号弧形闸门现场动力特性试验加速度传感器布置如图2所示.

图2 动力特性试验传感器布置图
在做闸门的动力响应试验时考虑到闸门在启闭运行时水流脉动压力主要作用在闸门结构的下部.根据闸门结构的特点和受力状况,在闸门上下主梁共选择7个测点来布置加速度传感器.10号和17号弧形闸门现场动力响应试验加速度传感器整体布置情况如图3所示,每个测点加速度传感器安装效果如图4所示.
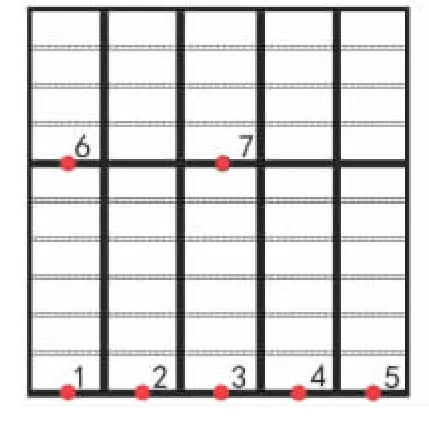
图3 动力响应试验传感器整体布置图

图4 传感器现场布置 效果图
2 闸门结构动力特性
2.1 基本原理
根据结构动力学理论,可将无限自由度的闸门离散为有限自由度系统,其振动微分方程为
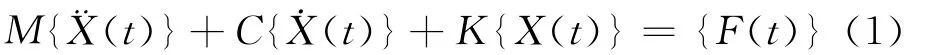
式中,M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;{¨X(t)}、{˙X(t)}和{X(t)}分别为结构的振动加速度、速度和位移列阵;{F(t)}为外荷载列阵.将式(1)进行拉普拉斯变换,得到系统在复域内的传递函数:

式中,n为系统自由度;{φi}为第i阶模态振型;Ki、Ci、mi分别为第i阶模态刚度、阻尼和质量;ω为圆频率;J为虚数.根据振型的正交性和互易原理,求得上述传递函数矩阵的任一列或任一行,就可构成系统传递函数矩阵,并通过迭代拟合,计算闸门结构的模态参数[9].
本次试验采用多点激振单点响应的方法.在试验中采用瞬态激励法,用激励力锤敲击闸门,对闸门施加一脉冲力F(t),由于脉冲信号的频率成份很丰富,在很宽的频带内各频率成分信号的能量几乎相等,可将结构的各阶模态激发出来[10].通过固定在闸门上A点的加速度传感器就可得到每次敲击所对应的加速度时程曲线.
2.2 试验结果
2.2.1 空载时弧形闸门的动力特性
试验工况上下游均为无水状态,用激励力锤敲击闸门.激励力锤冲击力典型时程曲线如图5所示.
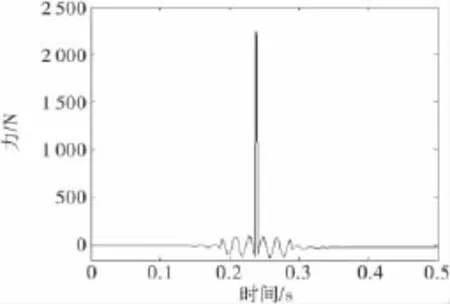
图5 激励力锤冲击力典型时程曲线
测得10号和17号两孔弧形闸门的基频分别为16.58Hz和15.63Hz.同时计算得两孔闸门的阻尼分别为1.6%和2.5%.10号闸门和17号闸门在空载下的加速度典型衰减曲线如图6所示.

图6 空载下闸门加速度衰减典型时程曲线
2.2.2 有载时弧形闸门的动力特性
试验工况为上游充满水,下游无水状态.按同样的方法用激励力锤敲击闸门.测得10号和17号闸门的基频分别为14.56Hz和13.67Hz.阻尼分别为2.4%和3.3%.10号闸门和17号闸门在有载下的加速度典型衰减曲线如图7所示.
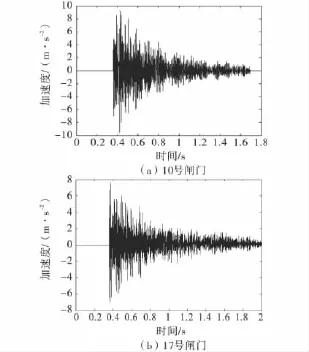
图7 有载下闸门加速度衰减典型时程曲线
3 闸门启闭过程的振动响应
闸门在开启过程中,受水流脉动压力的影响,闸门会产生振动.闸门结构自身的动力特性是影响闸门振动的内在因素,而水流脉动压力是影响闸门振动的外部因素.脉动压力的大小和频率对闸门振动的量级起着至关重要的作用,它的形成又与闸门开度,闸前水头以及堰面曲线等因素有关.由于现场试验条件的限制仅对10号和17号闸门在不同开度的开启和关闭过程进行了试验.
1)试验结果显示,10号闸门在启门过程中振动加速度最大值为12.84m/s2,有效值为2.36m/s2,发生在下主梁3号点;闸门在闭门过程中振动加速度最大值为8.30m/s2,有效值为1.85m/s2,发生在下主梁4号点.启门过程10号闸门加速度的典型时程曲线如图8(a)所示.
2)试验结果显示,17号闸门在启门过程中振动加速度最大值为8.85m/s2,有效值为2.85m/s2,发生在下主梁1号点;闸门在闭门过程中振动加速度最大值为8.07m/s2,有效值为2.77m/s2,发生在下主梁3号点.启门过程17号闸门加速度的典型时程曲线如图8(b)所示.
3)10号闸门在启门过程中,在到达0.18m开度时,加速度达到最大值.此后,闸门振动加速度随开度的增加逐渐减小,至4m开度以后逐渐变平缓.
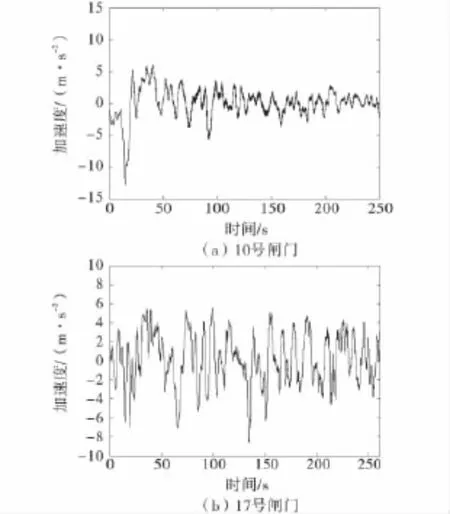
图8 闸门开启过程中典型加速度时程曲线
17号闸门在启门过程中,在到达3.55m开度时,加速度达到最大值.此后,闸门振动加速度随开度的增加逐渐减小,至5.63m开度以后逐渐变平缓.把10号和17号闸门下主梁中点实测加速度与闸门开度关系绘制成曲线,如图9所示.
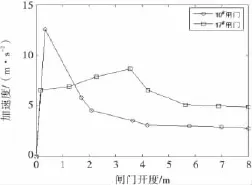
图9 振动加速度与闸门开度的关系
4 结 论
通过对太平哨电站泄洪坝10号和17号弧形钢闸门原型的现场试验结果进行归纳整理,得到以下结论:
1)频率和阻尼是反映结构动力特性的量化参数.从试验结果可以看出,空载工况下10号和17号闸门的基频非常接近,分别为16.58Hz和15.63Hz,相对误差为6.1%.尽管两孔闸门尺寸和材料完全相同,但由于闸门在制作和安装过程中存在的差异,以致于两孔闸门的基频不完全相同.
2)从实测结果可以看出闸门在有载工况下的基频和阻尼与空载工况下的基频和阻尼非常接近.并且由于有载工况下闸门门叶周边约束相对加强,有载工况下第一阶振型的阻尼要大于无载工况下相应阶次振型的阻尼,而有载工况下的基频要小于无载工况下的基频.
3)从图9可看出,10号闸门在0.18m开度时主梁出现加速度最大值,而17号闸门在3.55m开度时主梁出现加速度最大值.10号和17号闸门的振动加速度响应与闸门开度之间的关系曲线虽不完全相同,但闸门振动加速度与闸门开度的关系曲线变化趋势总体都是临界开度以前,振动加速度响应随开度的增大而增大,在临界开度时达到最大值.当超过临界开度后加速度响应又随开度的增加而逐渐减小,至变化逐渐平缓.
4)两扇弧形闸门的振动加速度实测值都不算特别大.鉴于目前尚没有统一的振动允许标准,为了确保闸门在启闭中的安全运行,建议避免在0.1~5m开度范围内长时间运行.
[1] 张友明.低水头弧形闸门振动问题研究[J].中国水利,2005(6):42-43,58.
[2] 练继建,彭新民,崔广涛,等.水工闸门振动稳定性研究[J].天津大学学报,1999,32(2):40-45.
[3] 潘锦江.闸门振动问题探讨[J].水利水电科技进展,2001,21(6):36-39.
[4] 潘锦江,陈小涛.浅谈闸门的振动问题[J].广东水利水电,2001(2):5-8.
[5] 黄廷璞,危 玢.我国低水头弧形闸门失事调查和初步分析[J].金属结构,1986,(2):18-26.
[6] 姜文潭,邵龙潭,张永利,等.高拱坝泄洪中孔弧形闸门振动试验研究[J].大连理工大学学报,1994,34(1):68-74.
[7] 朱召泉,卓家寿,陶桂兰.弧形钢闸门的动力稳定性研究进展[J].1999,19(5):27-29,37.
[8] 姬锐敏,蒋昌波,徐尚农,等.弧形闸门流激振动原型观测方法探讨[J].交通科学与工程,2013,29(2):71-78.
[9] 严根华.水动力荷载与闸门振动V水利水运工程学报,2001(2):10-15.
[10]刘礼华,袁文阳,孟吉复,等.凤滩弧形闸门局部开启原型振动试验研究[J].武汉大学学报:工学版,1997,30(3):30-34.

