基于PWM的高压直流电源设计

王归新 郭航彪 方 理

（三峡大学 电气与新能源学院，湖北 宜昌 443002）

近几年采用开关电源技术的高压电源研究较多，尤其是中小功率场合.常见的开关电源型高压直流电源，主要由整流滤波、高频谐振逆变、倍压整流3部分组成.随着新的电子元器件、新的电磁材料、新的电源变换技术、新的控制理论及新的专业软件的不断涌现，并不断被应用于开关电源，使得高压开关电源的性能不断提高，特点不断更新，出现了如频率高、效率高、功率密度高、可靠性高等新特性［1］.但伴随着先进技术的逐步应用，新的技术难题也随之而来，首先必须解决的是高压高频变压器的设计.

针对现有的高压直流电源技术以及存在的问题，本文通过将现有的电路有效组合，设计了一种新型高压直流电源，即基于PWM交流变换和12脉波整流的高压直流电源.

1 高压直流电源设计

传统的相控整流电源谐波电流较大，功率因数低，多电平电压型PWM整流电源开关数量多、控制复杂、应用技术不成熟，高压开关电源的高频升压变压器设计等难题尚未解决，因此本文将PWM交流变换电路和12脉波整流电路有机结合，设计了一个兼具两个电路优点的高压直流电源系统，系统框图如图1所示.该电源系统使用工频升压移相变压器和不可控整流桥组成的12脉波整流，其技术相对成熟，工作可靠性高；且AC／AC斩波器的功率器件运行环境好，通过调节交流PWM变换器的导通占空比，就可改变升压变压器原边电压，从而达到控制直流输出的目的.

图1 高压直流电源系统框图

1.1 PWM交流变换电路设计

由于三相PWM交流调压电路的每相都可等效为一个单相交流变换电路，因此其工作原理与单相电路相似［2］.如图2所示，为降压式三相PWM交流斩波调压电路结构，Q1和Q4、Q2和Q5、Q3和Q6为3对全控功率开关.由于三相电压线性相关，只存在两个独立变量，因此采取在一个时刻对其中两相斩波控制，而另一相保持导通，这样可比对三管同时斩波控制方式减小1／3的开关损耗.每相电压的大小关系决定了每对功率开关的工作方式.具体地，电压最小相的一对开关保持导通，其它两对开关以某一占空比进行PWM调制.如当B相电压最低时，让Q2、Q5持续导通，而对Q1和Q4、Q3和Q6分别进行互补的高频PWM控制，这样得到与输入正弦电压同相、等幅的一系列等宽的脉冲电压输出.L1、L2、L3和C4、C5、C6组成三相LC低通滤波器，可有效滤除开关次的高频谐波.

图2 降压式三相PWM交流变换电路

PWM交流变换电路的控制原理图在图3中给出.对输出高压直流通过霍尔传感器采样，作为电压反馈，与设定的基准值比较，误差值经PI调节器输出，再与高频三角载波比较得到高频脉冲.由于在1／3个工频周期内总有一对开关管保持导通，因此可通过过零检测和逻辑门来实现PWM波的分配.此处以A相电压最低来说明该逻辑电路脉冲分配的实现.三路相电压分别经过零比较器后，得到3路与线电压同步的工频方波信号Sab、Sbc、Sca.A相电压低于B相电压所以Sab为低，该信号经过反向器后再和信号Sca相与，同时由于A相电压最低，Sca为也高，那么Ta就为高，g1、g4都为高，因此与A相相连的IGBT（Q1和Q4）保持导通.同样的道理，B相电压最低时，Q2和Q5保持导通、C相电压最低时，Q3和Q6保持导通，这样就实现了PWM波的正确分配.当输入电压变化或者负载变化引起输出电压改变时，PI调节器的输出就会改变，PWM发生器的脉宽的变化就能够引起斩波器输出的变化，从而改变输出直流电压，使得输出无差地跟踪给定，保证高质量的稳定高压直流［3］.

图3 控制系统原理图

PWM交流变换电路的输入功率因数随着占空比的增大而提高，因此额定占空比设定越大越好.但是，为了保证系统有较宽的调节范围，占空比不能取得过大，因为如果占空比太大，在系统重载或输入较低时，系统有可能不能得到额定的直流电压［4］.由于整流输出连续时的直流电压平均值为

式中，Ue为移相整流变压器副边线电压的有效值.故系统的输出直流为

式中，Ui为系统输入交流线电压的有效值，k为移相三绕组变压器的变比，D为交流变换器中PWM波的占空比.

在输入电压最低且满载时，占空比最大，确定最大占空比Dmax，计算出k.当输入电压最高且空载时，为保证输出额定，则占空比为最小，计算最小占空比

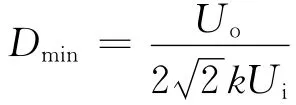
1.2 12脉波整流电路设计

12脉波整流电路是由两个相位差30°的变压器分别供电的两个三相整流桥构成的，如图4所示.由于这种结构各次谐波互相抵消，注入网侧的只有12k±1（k为正整数）次谐波，且其有效值与谐波次数成反比，而与基波有效值的比值为谐波次数的导数，所以可以降低交流输入侧的电流谐波、提高输出电压的质量［5］.

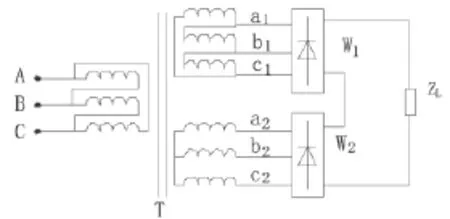
图4 12脉波整流电路原理图

2 仿真与分析

设定输入额定电压为380V（三相交流线电压），最大输入功率为40kVA，额定输出直流电压为4kV；开关频率取15K；最大占空比为0.94，变压器变比为4.6.负载取R＝400Ω，此时输出最大功率.图5为系统稳态时输入电压ui、电流ii和输出电压波形Ud.可以看出，输出电压稳定在4 000V，利用平均值计算模块可得输出平均电压为3 997V.在示波器内放大Y轴，发现输出直流的脉动峰峰值为10V，在合理的范围内.而且输入电流接近正弦，经傅里叶分析有THD＝4.71%，其中11和13次谐波电流最大，利用有功／无功测量模块以及数学计算模块测得功率因数约为0.98.图6为AC／AC斩波输出电压和输出电流波形.该仿真结果表明，额定负载时，本系统的稳态性能良好.

图5 稳态输入电压、电流和输出电压波形

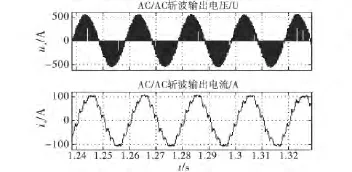
图6 AC／AC斩波输出电压、电流波形

动态性能的仿真包括系统在开机仿真、负载变动和输入电压波动情况下系统的调节性能.

2.1 系统启动仿真

系统满载启动的仿真波形如图7所示.可见，输出电压上升迅速，在10个工频周波内上升到了大约3 970V，15个周波后稳定在额定值，性能良好.

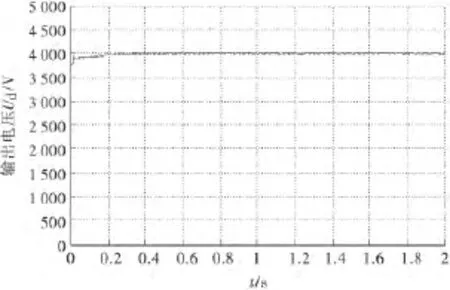
图7 系统上电过程的输出波形

2.2 负载调节仿真

仿真包括两个过程：负载从满载到半载和从半载到满载.输出电压仿真波形如图8所示.在4s前系统稳定在4 000V，4s这个时刻负载由半载变为满载，输出电压产生瞬间向下电压冲击，幅度小于200V左右，之后电压迅速上调，在0.2s内输出电压重新回到额定值.在7s时，负载由满载变为半载，此时也有瞬间电压尖峰，之后迅速稳定在4 020V，存在小幅误差，而在0.8s后输出电压调整额定输出电压.可见，负载变化时，系统反应较快，稳定性好.

图8 负载变动时的直流输出波形

2.3 输入电压变化仿真

该部分保持满载不变，而考虑输入电压波动范围在±10%时，系统的动态性能，波形如图9所示.在图9（a）中，在3s时，电压跌落10%，此时输出下降大约300V，在接下来的0.5s内回升到额定电压，稳定在4kV.同样，图9（b）中显示的是在3s时刻，输入电压上升10%，输出电压上升200V，0.5s后回到额定电压.因此，系统对输入电压改变的响应迅速.

图9 输入交流电压波动时的直流输出波形

3 实验结果

基于上述仿真，搭建了实验电路.图10给出了三相PWM信号的的分区图，可见，在每个工频周期被分为3个区间，每个区间内总有一相的两只开关保持导通，而另外两对IGBT进行高频通断控制，互补管的驱动信号死区时间的设置保证了电路的安全运行.

图10 3对IGBT的PWM信号分区

图11为满载（40kW电阻负载）情况下，直流输出电压及高压霍尔的输出波形.2通道为高压探头测得的输出直流电压波形，每格为1kV，可见输出稳定在4 000V；3通道为高压霍尔输出波形，此时在主电路输出为额定电压时，正好对应电压霍尔的5V额定电压值，测量准确.经测算系统效率高达97.2%.

图11 高压霍尔输出及电源输出电压波形

4 结 论

综合本文提出的新型结构高压直流电源的仿真分析和实验波形结果表明，本文提出的高压直流电源稳态误差小，启动迅速，动态调节能力快，稳定性好，从而验证了本文的科学性.

［1］ 冀 飞，王顺喜.高压直流电源技术的发展现状及应用［J］.高压电器，2004（8）：34－35.

［2］ 王志强，李国峰，刘志刚.基于LCC谐振变换器的高压直流电源设计［J］.2012，16（4）：4－6.

［3］ 姚为正，张国菊，何青莲.15kV高压直流电源的研制［J］.电力电子技术，2010，44（12）：65－66.

［4］ 解 大，乔歆慧，张延迟.Z源AC／AC变换器的谐波消除PWM 技术［J］.电机与控制学报，2011，15（4）：1－6.

［5］ 王兆安，杨 军，杨进军，等.谐波抑制和无功功率补偿［M］.2版.北京：机械工业出版社，2005.