新型压力调节阀内部流场的数值模拟
魏丹,宋花平,赵军
(1 北京化工大学机电工程学院,北京 100029;2 中国人民解放军总后勤部油料研究所,北京 102300)
目前国内已基本形成以干线为主的成品油管网,当要对局部区域临时供油时,一般采用装配式输油管线[1]从主干线导出油料。
成品油管线为适应长距离输送,内压一般在10MPa 以上,而便于转运和安装的装配式输油管线则采用轻量化设计,其最高工作压力一般都在6MPa 以下,所以油料导出时需要进行压力转换。
根据大压差和大流量的工作特点,设计了一种新型套筒式压力调节阀来调节管线间压差。供油时,成品油管线中的高压油料经过套筒式压力调节阀进行节流后,油料的压力降低。为了增强对接装置对野外工作条件的适应性,采用人工确定阀门开度和自力式稳流调节的技术路线,最终确保阀后流入装配式输油管线的压力降到安全工作允许值以下。
为了确定这种新型压力调节阀在工作时的安全可靠性,本文采用CFD 方法[2]对这种新型压力调节阀的内部流场情况及流量特性进行分析,也为以后的深入研究及性能优化奠定基础,提供理论依据[3—10]。
1 套筒式压力调节阀三维计算模型
1.1 结构及工作原理
阀内有两级节流套筒,公称通径为150mm,进出口总长为560mm,结构如图1 所示。流体先进入高压腔,经套筒节流孔一次减压后流入下腔,再经阀座孔二次减压后流入阀底从出口流出,工作原理如图2 所示。当有压力波动时,碟簧可起到稳定压力、流量的作用,节流孔的形状如图3 所示。调节阀芯的高度可改变套筒过流面积,从而调节流体通量。

图1 调节阀结构示意图
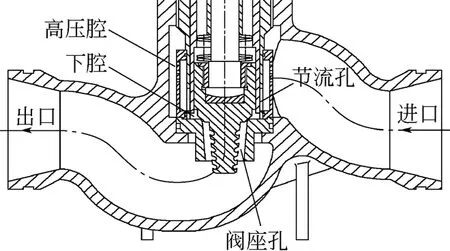
图2 调节阀工作原理示意图

图3 节流孔形状示意图
1.2 三维流道模型的建立
根据实际尺寸及装配关系,利用SolidWorks 软件建立起流通区域三维立体模型。为防止回流并使进出口处流动尽可能稳定,将阀进出口通道延长为管道直径5 倍左右。
为模拟不同工况,建立了各种开度的阀口流道模型,100%开度流道模型如图4 所示。
1.3 网格剖分
将三维几何实体导入到ANSYS ICEM 中进行计算前处理的网格划分ICEM,因阀内部流道几何形状复杂,故采用四面体单元结构化处理,并在节流孔及阀座孔处进行局部加密,以提高计算精度。
划分后网格数为51 万个左右,网格质量均大于0.3,可满足计算需要。对不同开度流道模型进行网格划分,即可得到相应网格文件,其中100%开度下流道网格如图5 所示。

图4 开度100%流道模型示意图

图5 调节阀100%开度流道网格示意图
1.4 求解
将网格文件导入到FLUENT 中,采用3D 双精度求解器、基于压力、稳态隐式求解方程及求解模型,计算得出Re=46267,属中等紊流状态,应选取标准k-ε模型,边界参数如表1 所示。流通介质为水,计算参数如表2 所示。初始化流场,设定收敛参数进行计算,迭代经1000 多步即可收敛。

表1 边界参数表

表2 流通介质参数表
2 计算结果及分析
2.1 流动分析
涡流对流动损失有重要影响,其位置和状态直接关系到节流降压效果,不同开度下的速度矢量分布如图6 所示。
流体在入口处以3.14m/s 均匀流动,进入高压腔后流通面积突然增大,流动开始发散形成涡漩,并在高压腔上部出现淤积死区。
流体经过高压腔套筒节流孔后,流通面积急剧减小,流速增大发生紊流。随着套筒开度的减小,节流孔处的流速依次增至31.62m/s、39.05m/s、44.05m/s 及47.17m/s,较入口流速大十几倍。在进入下腔阀座孔时流向改变,使得紊流增强。
在流过阀座孔后,流通面积突然扩大,流向再次改变,流动发散并产生涡漩,从而造成出口处流量不均,且有回流产生。
在关闭调节阀过程中,套筒节流孔面积随之缩减,流通截面亦缩小,流体通过节流孔及阀座孔后紊流逐渐增强,涡漩强度更加显著,从而提高了出口处流量的不均匀程度。
2.2 压力分析
压力调节阀内流场压力分布直接关系到减压效果,不同开度下对称面上流场压力分布如图7 所示。

图6 不同开度流速矢量分布图
进出口等径段压力变化比较平缓,高压腔内压力即入口压力为10MPa,当进入套筒节流孔时面积突然减小,根据孔板减压效应,涡漩剧烈紊动会损耗部分能量,从而使流体压力降低。且随着套筒开度的减小,节流孔处压力降依次为3MPa、3.2MPa、3.5MPa 及4MPa。

图7 不同开度流场压力分布云图
由下腔通过阀座孔流向出口时,由于流通面积减小及流向改变,紊乱加强,能量损耗增加,压力进一步降低,随着开度的减小,二次减压值依次为1MPa、0.8MPa、0.5MPa 和0,最终保证出口处压力保持在装配式输油管线许用范围之内。
随调节阀开度逐渐减小,套筒节流孔处压降逐渐增大,总体压降中一次减压比例渐增。开度为10%时,4MPa 压降基本全发生在节流孔处,二次减压阀座孔处减压几乎不起减压作用。
2.3 流量特性分析
调节阀流量特性中流体介质与阀体部件结构之间函数关系如式(1)所示。

式中,Q/Qmax为相对流量,是指压力调节阀某一开度时流量Q(m3/s)与全开时的流量Qmax(m3/s)之比;l/L 为相对位移,是指压力调节阀在某一开度时的阀芯位移l(mm)与全开位移L(mm)之比。
流体的流量特性大致分为4 种:直线型、等百分比型、修正等百分比型及快开型[11-12]。
通过CFD 计算可以得到调节阀的特性参数,从中选出10 个不同开度下压力调节阀流量计算数据如表3 所示。
压力调节阀模拟计算流量特性曲线如图8 所示。由图8 可以看出,出口压降不变,随着调节阀开度的增加,流量也随之增加,压力调节阀的流量特性曲线变化趋势接近快开型。

表3 压力调节阀流量计算数据表

图8 压力调节阀模拟计算流量特性曲线
2.4 试验验证
在某试验台上对该压力调节阀进行模拟试验,测得该阀在100%开度下的试验流量为0.0614m3/s。试验所得流量与模拟计算所得流量误差为11.5%。由于模拟计算时以光滑壁面处理,忽略了壁面摩擦阻力,故导致模拟计算流量高于试验流量,从而验证了数值模拟结果的可靠性,说明了数值模拟结果是比较准确的。
3 结 论
通过对新型套筒式压力调节阀不同开度下的内部流场进行CFD 数值模拟仿真,得到其内部流场压力、速度矢量分布的可视化结果,并分析得出调节阀的流量特性曲线,分析结果表明。
(1)流体在阀内流动时,由于流通面积不断变化,产生流动涡漩,影响出口流量均匀性,随着开度减小,涡旋增大,流量不均匀性更显著。
(2)套筒处流通面积突然收缩导致节流压降,开度与节流效果呈反比,同压降下,流量也相应减小。
(3)阀阻比为0.4 工况下,调节阀模拟计算得出流量特性为近似快开型。
(4)在保证阀两端压差情况下,全开度试验结果与数值模拟结果的误差在允许范围内。
数值模拟的结果验证了这种压力调节阀工作的可靠性以及计算模型及此采用方法的可行性。与实验结果比较,数值模拟的精度是可以信赖的,这也为日后该新型压力调节阀的流道设计及优化分析提供了数值依据。
[1] 陈涵,宋花平,赵军.装配式输油管道悬索跨越结构的分析计算[J].油气储运,2013(11):107-110.
[2] 李鹏飞,徐敏义,王飞飞. 精通CFD 工程仿真与案例实战[M]. 北京:人民邮电出版社,2011.
[3] Yang Qin,Zhang Zhiguo,Liu Mingyue,et al.Numerical simulation of fluid flow inside the valve[J]. Procedia Engineering,2011,23:543-550.
[4] Lisowski E,Rajda J. CFD analysis of pressure loss during flow by hydraulic directional control valve constructed from logic valves[J].Energy Conversion and Management,2013,65:285-291.
[5] Zhao Changqing,Liu Kai,Zhao Tong. Study and characteristic analysis on the valve of positive pulse measurement while drilling[C]//International Conference on Mechanical Design ,Magufacture and Automation Engineering,2014:5-10.
[6] Chattopadhyay Himadri,Kundu Arindam,Saha Binod K,et al.Analysis of flow structure inside a spool type pressure regulating valve[J].Energy Conversion and Management,2012,53:196-204.
[7] 王燕,徐晓刚,胡建,等. 多级套筒调节阀流场数值模拟与流量特性研究[J]. 石油化工自动化,2013,49(1):50-53.
[8] 樊达宜,栾秀春. 基于FLUENT 的节流管式调节阀结构优化[J].哈尔滨商业大学学报:自然科学版,2012,28(5):587-590.
[9] Yu Jue,Zhuang Jian,Yu Dehong.Modeling and analysis of a rotary direct drive servovalve[J]. Chinese Journal of Mechanical Engineering,2014,27:1064-1074.
[10] 潘永成,王勇,谢玉东. 基于CFD 的调节阀内流场流动特性研究[J]. 机床与液压,2011,39(1):5-7.
[11] 张双清,尹玉杰,明赐东. 阀门手册[M].北京:化学工业出版社,2013.
[12] 车渊博,李春,高坤,等. 调节阀内部流场的动态模拟及优化设计[J]. 能源研究与信息,2010,26(3):173-178.

