怎样利用几何作图法来求解物理问题

孙智勇 王金聚

（浙江省温州中学，浙江 温州 325000）

几何作图法充分运用“数形结合”的思想，把抽象而繁杂的物理过程转化成一幅幅具体而清晰的物理图像，将物理问题转化成一个个几何问题.通过几何图形所蕴含的物理意义从图中来寻求答案，既直观形象，又易于理解，且避免了一些繁琐的推理与计算，对启迪学生的思维、拓展学生的思路、提高学生的学习兴趣有着不可替代的重要意义.

下面通过几个具体实例，来展示一下几何作图法在高中物理教学中的妙用.

1 求作形状规则薄板的重心

质量分布均匀的物体，其重心的位置只跟物体的形状有关.形状规则且质量分布均匀的物体，其重心的位置就在物体的几何中心.由此，我们可以通过几何作图的方法，来求作均质且形状规则的物体的重心位置.

例1.有一块如图1所示的均匀薄板ABCDEF，试用作图法求出其重心的位置.

解析：求作重心的步骤如下.

（1）如图2所示，沿DC方向将薄板分割成上、下两个长方形，分别连接对角线找出其各自的重心O1、O2，则其整体的重心必在O1O2的连线上；

（2）如图3所示，沿BC方向将薄板分割成左、右两个长方形，分别连接对角线找出其各自的重心O3、O4，则其整体的重心必在O3O4的连线上；

（3）如图4所示，连接线段O1O2、O3O4，其交点O即为整体的重心.

图1

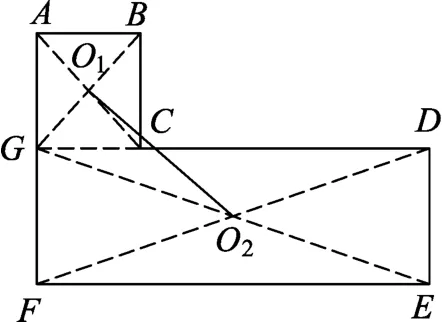
图2

图3

图4

2 作等时圆来解决最短时间问题

从竖直圆环的最高点沿任意光滑弦轨道滑到圆环的时间都相等，这样的圆被称为“等时圆”.当碰到竖直面内的最短时间问题时，我们不妨考虑一下画“等时圆”.

例2.如图5所示，质点自倾角为α的斜面上方定点O沿光滑的斜槽从静止开始下滑，为使质点在最短时间内从O点到达斜面，斜槽与竖直方向的夹角β应等于多少？

解析：如图6所示，以经过O点的竖直线上的一点O′为圆心，OO′为半径作圆，并使该圆与斜面恰好相切于A点，与OO′延长线交于B点.由于从O点由静止出发沿倾角不同的光滑斜面下滑的质点，到达圆周上不同点所需时间相等，所以可以看出，质点沿OA方向从静止开始滑到斜面上所需时间比沿其他方向滑到斜面上所需要的时间都要短.

图5

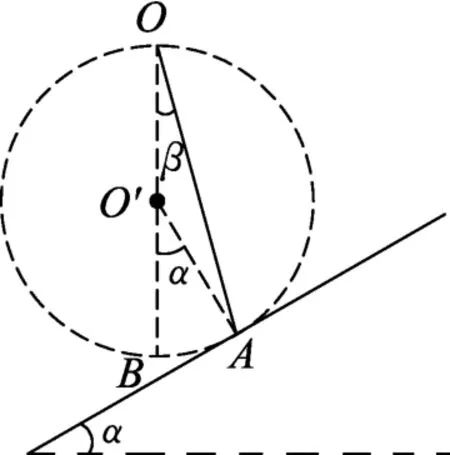
图6

3 作矢量三角形

对于3个共点力作用下物体的平衡问题，根据矢量三角形法则，我们常作出由3个力的图示矢量为边长的矢量三角形，然后由三角形中各边、角之间的数学关系求解.实际上，对于4个及更多的共点力平衡的情况，我们也可以想办法利用三角形法则，那就是先把某些力合成，合成到只剩3个力的时候，再作矢量三角形就可以了.

图7

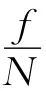
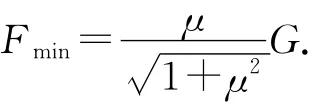
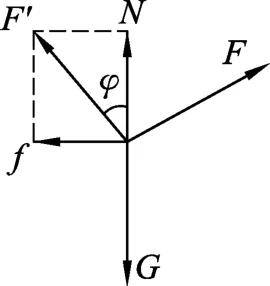
图8

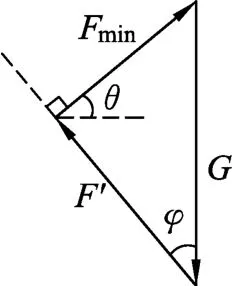
图9

4 作等效运动路线图

例如你先以速率v1慢跑了一段时间t1，接着以速率v2快跑了一段时间t2，当我们研究你运动的总时间的时候，我们不妨把这两种运动“合二为一”，即看作是你一直在慢跑或快跑.具体而言，若看作一直在慢跑，则慢跑的总路程为v1（t1＋t2）；若看作一直在快跑，则快跑的总路程则为v2（t1＋t2），这两种看法都能保证你运动的总时间未发生改变.对某些运动这种简单、等效的转换，对解一些复杂的运动问题有时会收到意想不到的效果.

例4.设湖岸MN为一直线，有一小船自岸边的A点沿与湖岸成α＝15°角方向匀速向湖中驶去.有一人自A点同时出发，他先沿岸行走一段路程再入水中游泳去追船.已知人在岸上行走的速度为v1＝4m/s，在水中游泳的速度为v2＝2m/s.试求船速至多不能超过多大，才能确保此人能够追上小船？

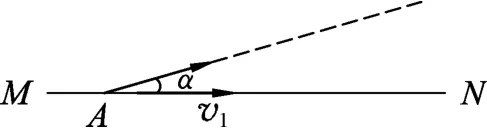
图10

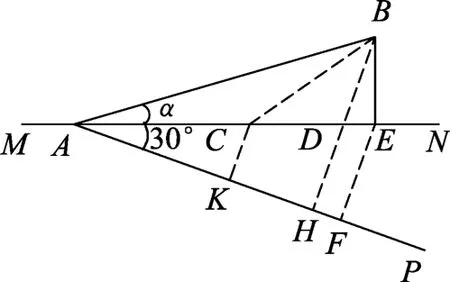
图11

解析：如图11所示，设人在B点追上船，则人到达B点可能有很多途径，如A→C→B，A→D→B，A→E→B等，这些途径中耗时最少的途径对应着允许的最大船速，作∠NAP＝30°，并分别作CK、DH、EF垂直AP，其中设BDH为直线.又设想MN线下方的湖岸也变成湖水区域，因为AC＝2CK，所以人由K点游泳到C点所用时间与人在岸上由A点走到C点所用时间是相等的.故人按题设情况经路径A→C→B所用时间与假想人全部在水中游泳游过路径K→C→B所用时间相等，同理，人按题设情况经路径A→D→B所用时间与假想人全部在水中游泳游过路径H→D→B所用时间相等，人按题设情况经路径A→E→B所用时间与假想人全部在水中游泳游过路径F→E→B所用时间相等.显然，在这些途径中，因为HDB是直线，因此所用时间最少.

由以上分析可知，人沿等效途径HDB游泳就能费时最少地刚好追上船，这对应着小船具有最大的船速，设为vmax，则有

因为△AHB是等腰直角三角形，所以AB＝BH.故得

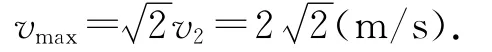
5 用圆的半径来表示大小不变的旋转矢量

在求解两个力的合成时，若其中的一个分力大小不变且合力的方向也保持不变，此时可以以合力的作用点为圆心，大小不变的那个力为半径作圆，然后来讨论另一个分力的变化情况，会使另一分力的变化情况非常明显地显示出来，这是个十分简洁明快的方法.

例5.在两个共点力合成的实验中，用A、B两个测力计拉橡皮条的结点，使其处于O处，如图12所示，此时α＋β＝90°.然后保持A的读数不变，当α角由图12所示的大小逐渐减小时，要使结点仍在O处，可以采用的办法是

（A）增大B的读数，同时减小β角.

（B）增大B的读数，同时增大β角.

（C）减小B的读数，同时减小β角.

（D）减小B的读数，同时增大β角.

解析：对结点O来说，受测力计A、B的拉力FA、FB和橡皮筋的拉力FT作用.当α逐渐减小时，要使结点的位置不改变，说明橡皮筋所受的拉力FT不能改变，由共点力的平衡条件可知，FA、FB的合力也不变.

图12

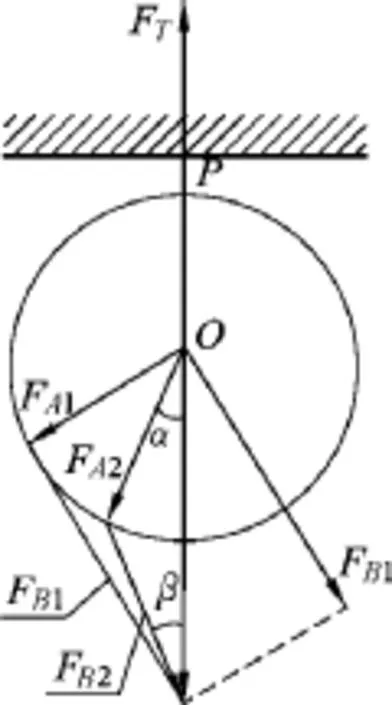
图13

以结点O为圆心，FA的大小为半径画圆，如图13所示，当FA绕O点逆时针方向转动，即α角逐渐减小时，由三角形法则作出一系列矢量合成图.由图可看出，FA1→FA2，α逐渐减小时，要使结点仍在O处，FB及β角均应减小，故正确选项为（C）.

6 利用同心圆解决光的折射问题

在光的折射现象中，如果已知入射光线的方向和两种介质的折射率，我们可以用几何作图法借助画同心圆来作出折射光线的方向.当光线由介质射向真空时，入射角增大到一定程度就会发生全反射现象，对于发生全反射现象的临界角的大小，类似地，也可以用画同心圆的办法求得.

6.1 利用同心圆求作折射光线

例6.如图14所示，一束光线由真空射向折射率为n的某种介质，入射点为O，试用圆规、刻度尺、三角板等工具用作图法作出折射光线的方向.

解析：作图法求作折射光线的步骤如下.

图14

（1）以入射点为圆心，以1和介质折射率n为半径做两个圆⊙P和⊙Q，如图15所示.

（2）延长入射光线，与⊙P交于点D，过D点做界面的垂线（或法线的平行线），交⊙Q于C点.

（3）连接OC即为折射光线.

上述作图法的证明：由图15中的几何关系可知，入射角i等于∠ODE，折射角r等于∠OCE.在直角△OED和直角△OEC中，可得

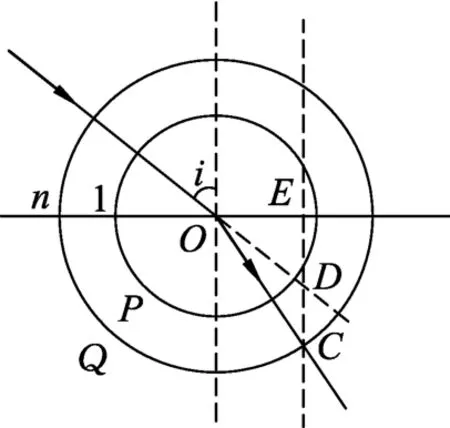
图15

6.2 利用同心圆求作全反射的临界角

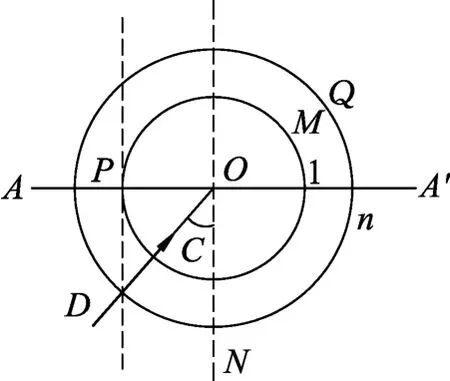
图16

如图16所示，一折射率为n的介质，介面为AA′，其上为真空，当光线由介质内射向介面AA′时，它发生全反射现象的临界角怎样用几何作图法作出呢？

作法：（1）作出过O点的法线ON；（2）以O为圆心，分别以1和n为半径作两个同心圆⊙M和⊙Q；（3）过介面与内圆的交点P作介面AA′的垂线交外圆于D点；（4）连接DO，则∠DON就是我们所要求作的临界角C.

作法证明：在图16中，由直角三角形ODP可以得到

不难看出，几何作图法直观、形象，一目了然，更易于凸显各物理量之间的相互关系，能使抽象问题具体化、复杂问题简单化.在中学课堂里恰当地介绍几何作图法，对提高学生的学习兴趣、拓展思路、启迪创新思维、提高分析问题与解决问题的能力，都具有重要的意义.