基于稀疏性贝叶斯极限学习机的气动调节阀多类故障诊断
谈斐祺, 谢 磊, 王挺任
基于稀疏性贝叶斯极限学习机的气动调节阀多类故障诊断
谈斐祺,谢磊,王挺任
(浙江大学控制科学与工程学系,杭州310027)
气动调节阀是工业过程中使用最广泛的终端执行机构之一,它的性能好坏直接影响控制回路的性能.将基于稀疏性贝叶斯的极限学习机(SBELM)方法运用于多类故障诊断,基于DAMADICS平台的典型气动调节阀多类故障模型数据通过SBELM进行训练.不仅能根据模型的先验知识和基于最大后验概率准则(MAP)的贝叶斯思想估计出模型输出的概率分布,而且能基于设定的性能指标自动剔除无用的训练样本,用一小部分观测数据达到多故障分类的目的,能训练出一个精确且紧凑的故障诊断模型.
气动调节阀;故障诊断;稀疏性贝叶斯极限学习机
气动调节阀属于控制回路中的终端执行机构,经过一段时间的频繁机械运动后性能会慢慢下降;这反过来影响到控制回路中控制器的输出,最终导致控制性能恶化.考虑到过程工业规模大,并且由成千上万的复杂控制回路组成,因此控制阀的自动化故障诊断具有重要意义.
气动调节阀除阀芯外,还由复杂的控制单元和执行单元组成,容易造成故障类型与症状不对应的情况;此外,由于工业现场中气动调节阀的数据难以获得,以及将故障诊断方法应用于工业现场中可能存在的问题,Bartys'等[1]开发1个阀门诊断平台——DAMADICS(Development and Application of Methods for Actuator Diagnosis in Industrial Control Systems),主要目的是比较和评价各种执行阀故障诊断算法.
Huang等[2]提出的极限学习机(ELM)近年来成为机器学习中比较热门的研究话题,已经证明只要单隐层前馈神经网络中的激励函数任意阶可导,那么任意给出隐层节点参数就可拟合任意的连续函数.ELM有2个缺陷:
(1)ELM的输出权重通过求解方程Hw=T的广义逆H-1实现[3],这种方法是最小二乘方法中的1种,很容易导致过拟合[4],并且在训练数据不能完全表征训练模型特征时加剧.
(2)ELM的精度很容易受训练样本大小的影响,再考虑到许多应用于实际案例的系统(如故障诊断系统)只提供一部分限制大小的内存,可能不够存储ELM模型,因此有必要在保证模型高精度的同时缩减模型的大小.
贝叶斯思想被用来训练ELM的输出权重,以获得更高的泛化能力[5].贝叶斯方法试着去估计输出值的概率分布,而不是完全匹配数据,因此能避免数据的过拟合.将稀疏性贝叶斯方法应用到ELM中解决回归性问题[5],输出权重具有基于共同超参数的先验高斯分布.此外,因为可能导致更复杂的贝叶斯学习(SBL)过程,所以文献[5]中并没有解决分类问题.
本文针对ELM提出1种新的稀疏性贝叶斯学习方法(Sparse Bayesian Extreme Learning Machine,SBELM),训练ELM分类器的输出权重,并且隐层参数像传统的ELM算法一样随机生成.通过基于一定的性能准则,逐步剔除无用的训练样本,因此,只利用一小部分训练集数据.更进一步的是,该算法可以将稀疏性拓展到多分类,并且能给出输出类关系的概率分布,而不是传统支持向量机(SVM)算法给出的生硬的二分类决策.因此,SBELM同时拥有SBL方法(高的泛化能力和稀疏性)和ELM算法(通用逼近性和高效的学习速度)的优势.
1 稀疏性贝叶斯极限学习机
1.1ELM简介
ELM最初被提出的形式是单隐层前馈神经网络(SLFN)[6],随后被拓展为隐层节点不需要神经元化的泛化SLFN[7].在ELM中,隐层参数不需要整定,给出1个有N个训练样本的训练集(xi,ti),i=1,2,…,N,每个样本xi都是1个d维的向量,相应的ti是期望的输出向量.含有L个隐层节点的ELM输出方程为

式中:β=[β1,β2,…,βL]T是含有L个节点的隐层与输出节点之间的输出权重向量;h(x)=[h1(x),h2(x),…,hL(x)]是对应于训练样本x的隐层输出矩阵.式(1)可以改写为

式中:H为N×L的隐层特征映射矩阵;H的第i行对应于训练集中第i个样本的隐层输出向量.式(2)的解为

式中,H-1是矩阵H的Moore-Penrose广义逆形式[3].
1.2SBELM模型
多分类相关向量机(MRVM)[8]通过引入中间变量Y,将原始的RVM扩展到多分类,这里的Y相当于中间的回归目标,并且在估计输出类别关系概率中很自然地引入多项概率分布.SBELM模型如图1所示.

图1 SBELM模型Fig.1 Model of SBELM
观测样本是ELM的隐层特征映射矩阵,基于此,得到训练核矩阵K∈RN×N.该模型的训练过程包括模型参数W∈RN×C的推导,并且WTK相当于1个投票系统,阐述哪种数据关系对模型具有合适分类特性的重要性.
为保证统计的可识别性,闭合的迭代推导中间变量Y假定为独立的标准高斯分布[9],按照文献[10]的直觉判断方法,回归量W表示某个数据点代表特定类的权重,中间变量Y表示类别关系排序系统.如给定1个样本n,指定其为第c类的原因是ycn的值最大.Y的连续特性不仅可以通过

进行多分类,而且可以通过多项概率分布方程[11]给出输出类别的概率分布

式中:u~N(0,1);Φ为高斯累积分布方程.
根据原始的相关向量机(RVM),W中的回归量wnc服从均值为0,方差为α-1nc的标准正态分布.αnc属于尺度矩阵A∈RN×C,并且服从超参数是τ、v的伽马分布[12].只要τ、v足够小(<10-5),尺度矩阵A可以限制W在零均值附近,并且拥有较小的方差.因此,最后只有一小部分回归量wnc非零,从而得到稀疏性.
训练流程包括基于标准期望最大准则(E-M)的模型参数连续更新.根据图1,推出回归量W的后验概率

式中:Ac由A的列对角矩阵得到,表示样本的尺度约束αic.
基于以上讨论,回归量的极大后验概率(MAP)估计值^W=arg maxWP(W|Y,A,K).给出1个类别,样本的权重参数会基于MAP的值自动更新:
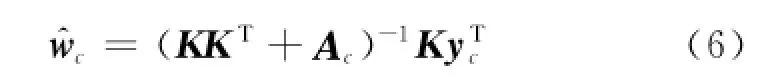
根据式(6)以及文献[10],得到中间变量Y的后验概率分布,是1个C×N维的截断高斯乘积.给出第i类,对于c≠i,E-step为


对于第i类

由伽马分布的均值给出超参数αnc的更新步骤.给定超参数τ、v,其后验概率分布为

上述伽马分布的均值为

每次迭代训练流程包括式(10)、(6)、(7)和(8)对模型参数的更新,直到满足设定的收敛准则.
1.3稀疏性和样本选择
SBELM模型采用一种快速的Ⅱ-型ML准则,在尺度矩阵A的限制下需要极大化模型的边际概率分布:

在该模型中,为得到1个可微的边际概率分布,遵循以下假定:每个样本n所对应的每个类别有共同的尺度参数αn.根据文献[13],对边际概率分布取对数,并将其分解成每个样本贡献程度的形式,这样就能得到添加、删除或者更新每个观测样本超参数αn的评价标准.
给出边际概率分布的对数形式

可得

式中:C=I+K T A-1K.根据文献[13]的分解形式

式中:C-i表示第i个样本移除后的值

由于C值的大小基于第i个样本的贡献程度,可将边际概率的对数值分解为
L(A)=L(A-i)+
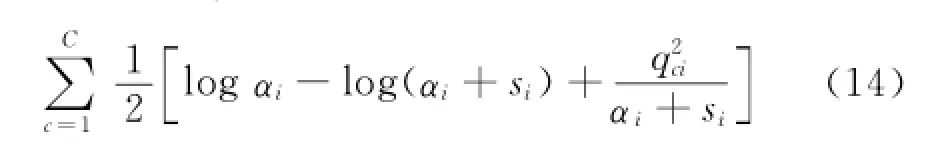
根据文献[13],定义“稀疏因子”si和新的多分类“质量因子”qci:

si定义核矩阵样本Ki和模型中已存在信息的重叠程度,即第i个样本中的描述信息有多少是由已训练过的样本表征的.qci表示第i个样本对描述特定类的作用大小.
将边际概率分解为特定样本的贡献成分后,得到基于αi的最大值,通过求导L(A)/αi=0,得到静态点:

定义量化因子

表明根据第i个样本对模型提供的额外描叙信息多少,判断其对边际概率的贡献程度.因此,在每次迭代过程中,一定能得到由M个积极样本生成的尺度矩阵A,使得θi>0i∈A.反之,如果有1个样本有正的θ值但不在A中,那么必须把它加进来;如果A中的某个样本具有负的θ值,则该样本必须移除.
1.4预测概率分布
由于式(4)不能直接被计算分析,需要采用数值估计方法,如蒙特·卡洛估计或文献[11]提出的随机变量采样.本文采用不同的正交逼近手段,求取式(4)的期望值后,对于任意给定的变量μ,有μ~N(0,1),式(4)可改写为

式中:e-u2为标准的Gauss-Hermite积分权重方程W(x).通常,2个零点足够达到1个很好的拟合效果,并且能给出与蒙特卡洛模拟一样的精确度.该方法的优点在于计算速度快于采样时间.
在大多数情况下,除高的辨识率外,还希望模型具有能接受的预测精度,即输出类别关系概率尽可能区分于随机猜测.为量化这种特性,定义预测概率分布:

式中:pnc表示在模型训练过程中,样本n属于特定类c的概率.预测概率分布表征模型在基于目标类、忽略其他类别关系的前期下,预测正确类别的置信区间.
2 DAMADICS平台应用
2.1DAMADICS简介
DAMADICS是由工程案例中研究学习并开发出来的用于评价故障检测和故障分离算法的1个平台[1].该平台的研究考虑到工业现场典型气动调节阀详细的物理和电气结构特性,以及执行阀在具有挑战环境下运作所需的典型工程要求.该平台的执行阀包括控制阀、气动执行机构和定位器等3部分,见图2.图中,D/A是数据采集单元;PC是定位器处理单元;E/P是电气转换器;V1、V2和V3是旁路阀;DT表示阀杆位移变送器;PT表示压力;FT代表管道介质流量;TT表示介质温度.

图2 DAMADICS的执行阀结构Fig.2 Structure of DAMADICSactuator
在气动调节阀中,故障可以发生在控制阀、气动执行机构、电气转换器以及变送器等任意地方,该模型被设计成可以仿真19种特定故障类型,见表1.
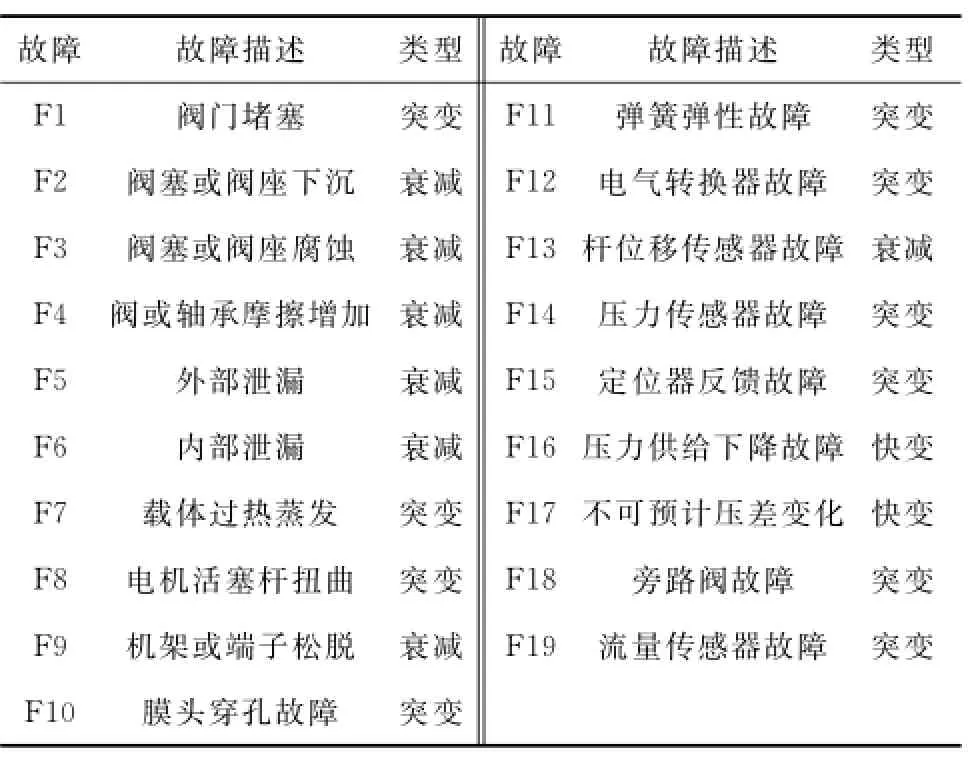
表1 故障描述Tab.1 Fault specification
该平台气动调节阀仿真模型基于实际工业现场中典型的气动执行阀工程经验知识和机理模型描述.模型的调整和校验通过欧洲Lubin的1个制糖厂控制锅炉进水流量的气动调节阀实际运行数据验证.仅有的5个被测变量和控制器的输出信号被用作故障诊断:控制器输出信号CV,阀前、阀后的压力p1和p2,介质流速F,介质温度T1以及阀杆的位移X,见图3.该模型可用于生成正常和故障状态下气动调节阀的数据,提供不同故障诊断算法的训练集和测试集数据.

图3 执行阀的输入输出模型Fig.3 Inputoutput model of actuator
2.2仿真实验
基于MATLAB/SIMULINK的“DABLIB”库被开发出来,以支持DAMADICS平台.该库围绕执行阀模型开发,主要包括执行阀模块、数据生成模块和通用模块等3个封装模型.执行阀模块的所有输入输出都加入白噪声干扰.数据生成模块产生用于故障诊断的各类数据集,见图4.该模块支持产生单一故障类型的数据,并且有“故障选择”和“故障类型”2个变量可选.所有数据的采样时间均为1 s.

图4 数据生成模块Fig.4 Datageneration block
基于DAMADICS平台,验证将SBELM算法用于气动调节阀多类故障诊断的性能.考虑到气动调节阀的渐变性故障包含许多不确定性,并且处于不稳定状态,不适合用于数据驱动的建模,因此只考虑执行阀突发性故障.选择10种典型的突发性故障F1、F7、F8、F10、F11、F12、F14、F15、F16和F19作为训练集.气动调节阀的输入信号CV是个均值为50%的低频正弦信号;流经执行阀水的温度设为常量;阀前、阀后压力p1和p2由幅度、频率合适的正弦信号驱动.仿真的注意点如下:
(1)所有数据集的特征变量数据根据其实际测量范围归一化到[-1,1];
(2)SBELM的隐层激励方程是Sigmoid函数

a和b是[-1,1]随机给定的隐层参数;
(3)每种故障类型的训练样本个数是100(包括正常情况下的样本),故训练集的维度是1 100×6.
仿真结果表明,典型样本个数是1 100个中的25个,即训练核矩阵和模型参数矩阵稀疏化为Ksparse∈R 25×25,Wsparse∈R 25×11,极大地缩减模型的规模.因此,该紧凑模型可用于快速预测测试集样本.给定100个故障F1的故障数据作为测试集的样本,结果如下:

输出类别关系概率分布是个100×11的矩阵,矩阵的每行表示测试样本,每列表示不同的类别.矩阵中的每个元素pij表示第i个样本属于第j类的概率,j=0,1,7,8,10,11,12,14,15,16,19(0代表正常无故障的情况).仿真结果显示,故障F1的精度是88%,表明该模型的性能较好.SBELM算法的最大亮点在于除有较高的精度外,还给出预测的概率分布,而非生硬的二分类决策,对于工业应用具有实际意义.
测试所有故障数据后,得到每种故障的预测精度,见表2.总体而言,SBELM故障的诊断性能很好,故障F8和F14预测精度低的原因是两者的故障症状非常相似,不易分离.
将SBELM的性能与SVM,RVM以及ELM等其他机器学习的算法对比,见表2.可知,SBELM利用一小部分训练样本就取得有竞争力的结果;SVM和RVM原本用于处理二分类的情况,在被不同方法改进后能应用于多分类的问题,但在多分类模型训练过程中仍存在参数难以整定等缺陷.

表2 结果精度比较Tab.2 Results comparison of recognition rate
3 结 语
提出基于ELM的贝叶斯稀疏方法,并给出输出预测类别关系的概率分布,最后将其应用于DAMADICS平台上的气动调节阀多类故障诊断,取得较好的效果.SBELM结合ELM的全局拟合能力和贝叶斯稀疏性手段训练模型参数,可以自动整定模型参数,使其中大部分参数趋于0,保证模型的稀疏性和高效性.通过极大化边际概率分布而非最小化训练误差的手段,SBELM不会产生数据过拟合的问题.从气动调节阀故障诊断的仿真结果看,SBELM的精度较好.
考虑到训练过程中涉及样本选取的过程,SBELM的训练时间比ELM长,因此SBELM训练过程还可进一步优化.此外,本文只考虑突发性故障类型而忽略渐变性故障类型,主要考虑渐变性故障数据不稳定,不适合用于建立数据模型,后续需要考虑怎样消除渐变性故障数据对模型造成的不确定性.
[1]Bartys'M,Patton R,Syfert M,et al.Introduction to the DAMADICS actuator FDI benchmark study[J]. Contr Eng Practice,2006,14(6):577-596.
[2]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1-3):489-501.
[3]Banerjee K S.Generalized inverse of matrices and its applications technometrics[J].Taylor&Francis Group,1973,15(1):197.
[4]Bishop C M.Pattern recognition and machine learning[M].New York:Springer-Verlag,2006.
[5]Soria-Olivas E,Gomez-Sanchis J,Jarman I,et al. BELM:Bayesian extreme learning machine[J].Neural Networks,IEEE Trans,2011,22(3):505-509.
[6]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]//Proc Int Joint Conf Neural Networks.Budapest,Hungary,2004:985-990.
[7]Huang G B,Chen L.Enhanced random search based incremental extreme learning machine[J].Neurocomputing,2008,71(16-18):3460-3468.
[8]Psorakis I,Damoulas T,Girolami M A.Multiclass relevance vector machines:sparsity and accuracy[J]. Neural Networks,IEEE Trans,2010,21(10):1588-1598.
[9]Albert J H,Chib S.Bayesian analysis of binary and polychotomous response data[J].J Am Stat Assoc,1993,88(422):669-67.
[10]Damoulas T,Girolami M A.Combining feature spaces for classification[J].Pattern Recognition,2009,42(11):2671-2683.
[11]Damoulas T,Girolami M A.Probabilistic multi-class multi-kernel learning:on protein fold recognition and remote homology detection[J].Bioinformatics,2008,24(10):1264-1270.
[12]Tipping M E.Sparse Bayesian learning and the relevance vector machine[J].J Machine Learning Res,2001(1):211-244.
[13]Tipping M E,Faul A C.Fast marginal likelihood maximisation for sparse Bayesian models[C]//Proc 9th Int Workshop Artificial Intelligence&Stat.Key West,USA,2003:1-13.
(编辑吕丹)
MultiFault Diagnosis of Pneumatic Control Valve with Sparse Bayesian Extreme Learning Machine
TAN Feiqi,XIE Lei,WANG Tingren
(Department of Control Science and Engineering,Zhejiang University,Hangzhou 310027,China)
Pneumatic control valve is the most widely used actuator in industrial process and its property is closely connected with the performance of control loop,so pneumatic control valve fault diagnosis is of great importance.The fault diagnosis method based on sparse Bayesian extreme learning machine (SBELM)of multiclass classification was introduced.The multi-fault diagnosis model of control valve with the data based on development and application of methods for actuator diagnosis in industrial control systems(DAMADICS)is trained through SBELM.The proposed method allows for estimating the marginal likelihood of network outputs based on the priori knowledge of the model and the criterion of maximum a posterior(MAP),and automatically pruning out unnecessary samples based on a certain performance criterion during training phase,which utilizes only a very small fraction of the available observation data achieving the goal of multiclass discrimination,thus results in an accurate and compact fault diagnosis model.
pneumatic control valve;fault diagnosis;sparse Bayesian extreme learning machine(SBELM)
TQ 35
A
1671-7333(2015)03-0271-06
10.3969/j.issn.1671-7333.2015.03.012
2015-01-16
谈斐祺(1990-),男,硕士生,主要研究方向为工业过程控制阀故障诊断.E-mail:tanfeiqi@qq.com
谢磊(1979-),男,副教授,博士,主要研究方向为工业过程故障诊断和性能评估.E-mail:leix@iipc.zju.edu.cn

