光伏系统模糊PSO的MPPT控制

李继生，李金羽，游国栋，雷淑英

（天津科技大学电子信息与自动化学院，天津 300222）

光伏系统模糊PSO的MPPT控制

李继生，李金羽，游国栋，雷淑英

（天津科技大学电子信息与自动化学院，天津 300222）

在局部阴影条件下，光伏阵列的功率-电压特性曲线呈现多峰状，传统最大功率点跟踪方法出现搜索精度低和收敛速度慢的问题.针对此问题提出一种基于模糊控制的粒子群优化算法，采用模糊控制器对粒子群优化算法的惯性权重ω进行优化，实时调整参数，使光伏阵列在光照强度变化时有较好的动态特性和稳态性能.分别采用常规PSO算法和模糊PSO算法在相同条件下对系统进行仿真，结果表明所提出的算法在局部阴影条件下能快速跟踪外部环境变化，且准确地工作在最大功率点.

最大功率点跟踪；局部阴影；粒子群优化算法；模糊控制

本文提出一种基于模糊控制的粒子群优化算法，对光伏阵列的最大功率点进行跟踪控制，根据粒子群算法中参数的特点，采用模糊控制器优化粒子群算法的惯性权重ω，当光照强度发生变化时，能跟踪控制并实时调整参数值，避免陷入局部最优值.最后采用常规粒子群优化算法和模糊粒子群优化算法对仿真模型进行对比分析.

1 光伏电池的建模

通常，太阳能光伏发电系统的电气特性表示为功率对电压（电流/占空比）和电流对电压的比［10］.光伏电池的特性曲线呈非线性.图1为光伏电池的等效电路.

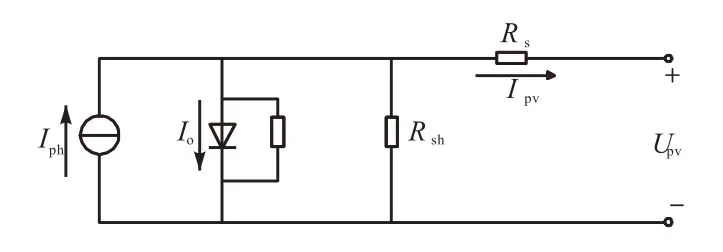
图1 光伏电池的等效电路Fig. 1 Equivalent circuit of a PV array

光伏发电系统产生电流的数学模型为

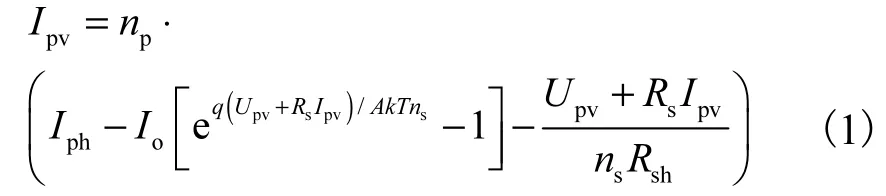
式中：Upv和Ipv分别为光伏输出电压和电流；Rs和分别为光伏电池的串联和并联电阻；q为电子电荷（1.6×10-19C）；Iph为光生电流；Io为二极管电流；A为光伏电池中半导体器件的P-N结系数；k为波尔兹曼常数（1.38×10-23J/K）；T为热力学温度；np和ns分别为光伏电池的串联数目和并联数目.

2 PSO算法在多峰MPPT中的应用

2.1 PSO算法

粒子群优化算法（PSO）是从鸟群觅食这一行为中推演产生的，它通过粒子群中各个粒子的不断迭代、更新来找寻最优解［11］.粒子根据其追随的2个“最优值”使个体得到更新.其中一个“最优值”指粒子从初始至当前时刻内的最好位置，即个体最优值（Pbest），另一个“最优值”是种群里全部粒子至当前时刻为止找到的最好位置，即全局最优值（Gbest）.第t+1次迭代时，第i个粒子的速度及位置通过式（2）和式（3）更新.

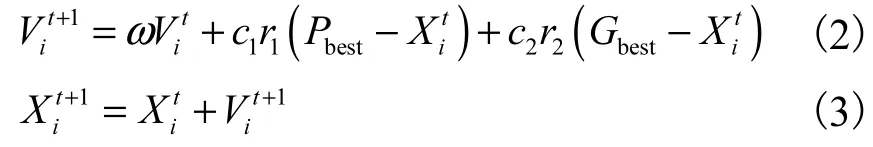
式中：t为迭代次数；ω为惯性权重；c1和c2为学习因子；1r和r2为［0，1］上的随机数.

2.2 PSO算法在多峰MPPT中的应用

当光伏电池所受光照强度均匀时，光伏电池的P-U、I-U特性曲线呈单峰状；当光伏电池所受光照强度不均匀，即存在局部阴影情况时，P-U、I-U特性曲线呈多峰状，这种情况下很容易产生误判，将追踪到的局部极值点当成全局极值点［12］.局部阴影下光伏阵列的输出特性见图2.其中，曲线a和曲线b分别表示光照强度均匀和不均匀时的特性曲线.

图2 局部阴影下光伏阵列的输出特性Fig. 2Output characteristics of the PV array under partial shade

在局部阴影条件下，采用粒子群优化算法进行最大功率点跟踪时，需要对粒子群的参数进行初始化，以往对参数的设置基本上是依据经验.文献［11］指出，粒子的维数是取决于与其相关的优化问题；粒子的最大速度决定当前时刻位置与最优值间区域的分辨率；学习因子取值过小或过大，都会导致粒子远离目标区域.本文参考现有文献资料，并结合实验，设置PSO算法的参数为：粒子总数N=100，粒子初始速度V0=0，最大速度限定值Vmax=2，学习因子c1==2，惯性权重ω=0.4.选择光伏阵列输出总功率函数作为适应函数.由式（2）、式（3）可知，每次迭代时，粒子的速度和位置会更新.

2.3 特性分析

为准确且快速地获得全局最优解，粒子群优化算法的参数设置至关重要，而惯性权重ω又在参数中占据主要地位，它决定粒子的此次迭代速度对下次迭代速度的影响程度.在算法中，若惯性权重保持恒定不变，则无法保证局部搜索与全局搜索之间的平衡.惯性权重过小或过大也会对算法造成不利影响：惯性权重过小，虽然能提高算法的局部搜索能力，但会延长收敛时间，容易陷入局部最优值；惯性权重过大，会导致精确解的搜索变困难，难以获得全局最优值［13］.只有当惯性权重取值恰当时，才能既避免陷入局部最优值，又快速获得精确解.

3 基于模糊控制的粒子群优化算法MPPT

本文将模糊控制器加入到粒子群算法中，采用模糊控制来调整粒子群惯性权重ω，避免粒子陷入局部最优值［14-15］.在充分考虑粒子群个体分布、进化程度及最优适应度对惯性权重的影响后，建立相应的模糊规则，通过计算最近3次迭代中粒子的平均适应度值，优化惯性权重ω.

按照以下规则判断并调整参数ω：

其中，ε为给定的趋近于零的正实数；γω为隶属函数的最大值（本文中γω=1）.

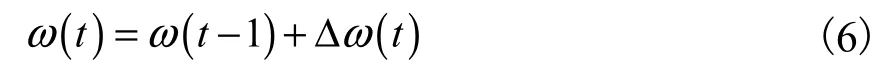
模糊控制器包括模糊化、模糊推理和解模糊3个部分，它将输入量模糊化，采用模糊规则进行模糊推理，最后通过反模糊化，使输出量精确化.模糊控制器框图如图3所示.

图3 模糊控制器框图Fig. 3 Diagram of the fuzzy controller

输入量和输出量均离散化为11级，分别标准化到［-1，1］和［-0.1，0.1］；模糊子集均为｛NB，NL，NM，NS，ZE，PS，PM，PL，PB｝，即｛负大，负较大，负中，负小，零，正小，正中，正较大，正大｝.输入量和输出量隶属度函数分别如图4、图5所示.

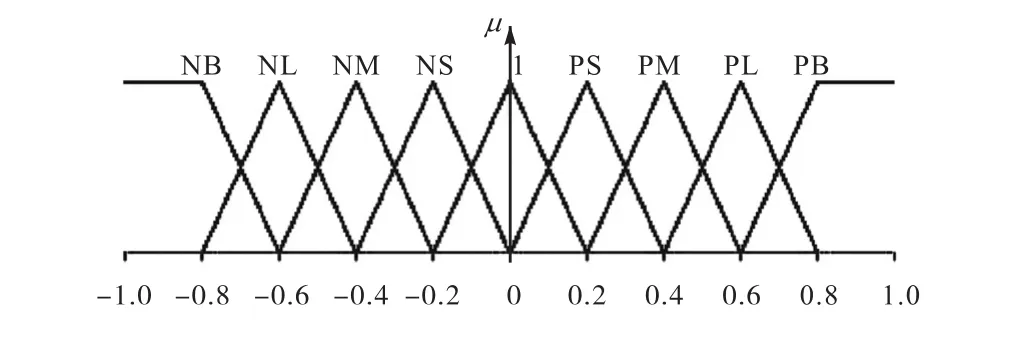
图4 输入量Δ2（x，t -1）和Δ2（x，t ）的隶属度函数Fig. 4 Member functions of Δ2（x，t -1）and Δ2（x，t ）

图5 输出量Δω的隶属度函数Fig. 5 Member function of Δω

根据粒子群算法特点、参数特性及其对算法的影响，制定模糊控制规则和反模糊化表.模糊控制规则共81条，见表1.

表1 的模糊控制规则Tab. 1 Fuzzy control rules for

表1 的模糊控制规则Tab. 1 Fuzzy control rules for

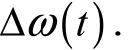
表2 反模糊对应值的规则表Tab. 2 Defuzzification control rules for

表2 反模糊对应值的规则表Tab. 2 Defuzzification control rules for

?

算法的实现步骤如下：

（1）根据设定算法的各个参数，对粒子的位置及速度进行初始化；

（2）根据适应函数计算各粒子的适应值，确定个体历史最优值Pbest和全局最优值Gbest；

（5）按照式（2）、式（3）更新各粒子的速度及位置，根据函数判断当前粒子个体历史最优值、粒子群是否处在全局最优值，更新Pbest和Gbest；

（6）判断是否满足终止条件，若满足则输出结果并结束算法，否则返回步骤（3），继续执行.

4 仿 真

根据本文提出的改进的粒子群优化算法，采用Matlab/Simulink对10个额定功率为850，W的系列模块进行仿真，仿真模型如图6所示.设置光伏模块的参数为：输出电压300，V，升压电感0.3，H，滤波电容2，200，µF，开关频率4，kHz.

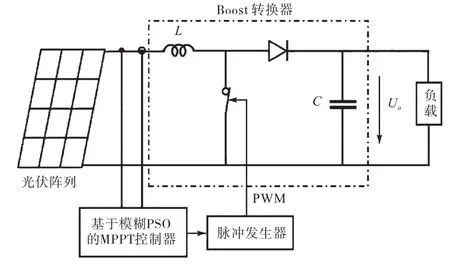
图6 基于模糊PSO的仿真模型Fig. 6 Simulation model based on fuzzy PSO

局部阴影条件下，为了比较常规PSO与模糊PSO（MPPT）的性能，在相同条件下对两种方法进行仿真，采用不同的分布式辐射水平进行测试：7个非阴影模块接收的辐射为1，000，W/m2，另外3个部分阴影模块接收的辐射水平分别为800、500和100，W/m2.光伏阵列的输出功率如图7所示.

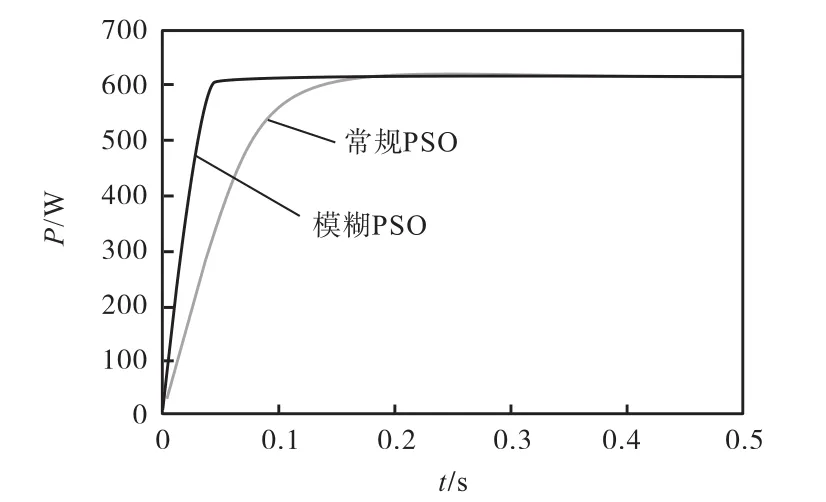
图7 局部阴影条件下光伏系统的动态响应Fig. 7Dynamic response of the PV system under partially shaded conditions

由图7可以看出，局部阴影条件下，常规PSO算法与模糊PSO算法均能跟踪到最大功率点.常规PSO算法在整个MPPT跟踪过程中功率波动较大，跟踪速度较慢，而模糊PSO的全局极值点跟踪速度较快，振荡幅度较小，稳态精度较高.

为进一步验证该方法，对非阴影模块使用具有不同辐射水平的相同的局部阴影条件.辐射水平在0.5，s内从500，W/m2变化至1，000，W/m2，再在1，s内从1，000，W/m2变化至500，W/m2.结果见图8.可以看出：即使是在变化的天气条件下，MPPT也能在较短时间内扫描并跟踪全局极值点；在光照强度发生剧烈变化的情况下，与常规PSO相比，采用模糊PSO的系统到达稳定所需的时间更短，波形畸变更小，具备良好的跟踪性能.

5 结 语

本文提出了一种基于模糊控制的粒子群优化算法，用于跟踪控制局部阴影下光伏阵列的最大功率点.将模糊控制器加入到粒子群优化算法中，优化粒子群算法中的参数ω，建立光伏阵列数学模型，并在局部阴影条件下进行仿真研究.通过仿真分析可以看出：与传统粒子群算法相比，模糊粒子群算法的跟踪速度更快，稳态精度更高；本文提出的算法在不同阴影条件及阴影条件变化时均能有效追踪到最大功率点，并能有效减少采用常规PSO时在最大功率点附近的振荡幅度.

［1］ 周林，武剑，栗秋华，等. 光伏阵列最大功率点跟踪控制方法综述［J］. 高电压技术，2008，34（6）：1145-1154.

［2］ 杨水涛，张帆，丁新平，等. 基于输入-输出参数的光伏电池最大功率控制的比较［J］. 电工技术学报，2009，24（6）：95-102.

［3］ 吴理博，赵争鸣，刘建政，等. 单级式光伏并网逆变系统中的最大功率点跟踪算法稳定性研究［J］. 中国电机工程学报，2006，26（6）：73-77.

［4］ 刘晓艳，祁新梅，郑寿森，等. 局部阴影条件下光伏阵列的建模与分析［J］. 电网技术，2010，34（11）：192-197.

［5］ 肖景良，徐政，林崇，等. 局部阴影条件下光伏阵列的优化设计［J］. 中国电机工程学报，2009，29（11）：119-124.

［6］ 朱艳伟，石新春，但扬清，等. 粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用［J］. 中国电机工程学报，2012，32（4）：42-48.

［7］ Noguchi T，Togashi S，Nakamoto R. Short-current pulsebased adaptive maximum-power-point tracking for a photovoltaic power generation system［J］. Electrical Engineering in Japan，2002，139（1）：65-72.

［8］ Kobayashi K，Takano I，Sawada Y. A study of a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［J］. Solar Energy Materials and Solar Cells，2006，90（18）：2975-2988.

［9］ Miyatake M，Toriumi F，Endo T，et al. A novel maximum power point tracker controlling several converters connected to photovoltaic arrays with particle swarm optimization technique［C］//2007 European Conference on Power Electronics and Applications. Piscataway：IEEE，2007：1-8.

［10］ Alajmi B N，Ahmed K H，Finney S J，et al. A maximum power point tracking technique for partially shaded photovoltaic systems in microgrids［J］. IEEE Transactions on Industrial Electronics，2013，60（4）：1596-1606.

［11］ 吴海涛，孙以泽，婥孟. 粒子群优化模糊控制器在光伏发电系统最大功率跟踪中的应用［J］. 中国电机工程学报，2011，31（6）：52-57.

［12］ Gen M，Yun Y S. Soft computing approach for reliability optimization：State-of-the-art survey［J］. Reliability Engineering & System Safety，2006，91（9）：1008-1026.

［13］ 赵阳，符强，王镭，等. 基于粒子群算法的最大功率点跟踪方法研究［J］. 电力电子技术，2010，44（6）：32-33.

［14］ 刘琳，陶顺，郑建辉，等. 基于最优梯度的滞环比较光伏最大功率点跟踪算法［J］. 电网技术，2012，36（8）：56-61.

［15］ 任海鹏，郭鑫，彧杨，等. 光伏阵列最大功率跟踪变论域模糊控制［J］. 电工技术学报，2013，28（8）：13-19.

责任编辑：常涛

MPPT Control of PV System Based on Fuzzy PSO Algorithm

LI Jisheng，LI Jinyu，YOU Guodong，LEI Shuying
（College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China）

Under partially shaded conditions，multiple local maximum can be exhibited on the power-voltage characteristic curve. To solve the problem of the low rate of searching precision and convergence using conventional maximum power point tracking methods，a control algorithm based on Particle Swarm Optimization algorithm using fuzzy control was proposed. Fuzzy controller was used to optimize the inertia weightωof PSO algorithm to ensure that the system has better dynamic response speed and steady-state accuracy when solar radiation changes. Simulation was performed with the PSO method and Fuzzy PSO method under the same condition，and the results indicate that the proposed global MPPT algorithm can quickly and accurately track the global maximum under partially shaded conditions.

maximum power point tracking（MPPT）；partially shaded conditions；particle swarm optimization（PSO）algorithm；fuzzy control

TM914 文献标志码：A 文章编号：1672-6510（2015）01-0073-05

10.13364/j.issn.1672-6510.20140086

由于传统能源和环境问题的限制，清洁可再生能源越来越受到国内外研究者的关注.太阳能因其分布广、无污染等优点而具有良好的应用前景［1-3］.研究者通常采用最大功率点跟踪（maximum power point tracking，MPPT）技术提高光伏电池的利用率.然而，光伏系统的输出电压和电流之间存在非线性关系，且在局部阴影条件下，系统的P-U特性曲线有多个峰值，易发生误判［4-6］.

2002年，Noguchi等［7］提出一种基于短路脉冲的MPPT算法，可快速扫描P-U特性曲线来确定比例参数，找到全局极值点，但该方法会引起瞬时功率的损耗.2003年，Kobayashi等［8］设计了一个使用监控单元的两级MPPT，在第1阶段，当P-U特性曲线均匀时，它的工作点移动到最大功率点；在第2阶段，采用增量电阻法来定位实际的最大功率点，但该方法在局部阴影情况下可能会陷入局部极值点.2007年，Miyatake等［9］在光伏阵列中应用粒子群优化算法，它易于实现，搜索速度较快，但是其参数通常依据经验设置，缺乏固定的参考模型，对算法的收敛性及稳定性也缺乏严谨的数学分析.因此，考虑将粒子群优化算法与其他控制方法相结合，弥补粒子群优化算法的局限性，进而提高系统精度.

2014-05-29；

2014-09-05

天津市自然科学基金重点资助项目（13JCZDJC29100）

李继生（1963—），男，辽宁锦州人，教授，lijish@tust.edu.cn.