线段图帮我顺利解题
2015-07-25 02:06马嘉杰
读写算·高年级 2015年2期
马嘉杰
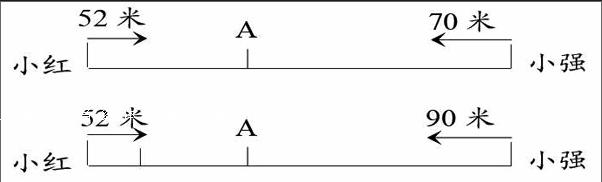
数学课外阅读时,我遇到了这样一道题:小红和小强同时从家里出发相向而行。小红每分钟走52米,小强每分钟走70米,两人在途中的A处相遇。若小红提前4分钟出发,且速度不变,小强每分钟走90米,则两人仍在A处相遇。小红和小强两家相距多少米?
这是一道相遇问题,两人同时出发相向而行,相遇时,两人所走的路程和就是两家的距离。题中只告诉我们两人的速度,要求两家的距离,得先找到相遇的时间才行呀。
怎样找到相遇时间呢?我头乱如麻。对了,画线段图!
线段图画好后,我的思路立刻变清晰了。比较两次行走的线段图,第一次小红与小强在A处相遇,第二次还是在A处相遇,两次相遇在同一地点,说明小红先后两次走的路程相同,小强两次走的路程也相同。对小红来说,两次走的路程相同,速度不变,那么小红先后两次所走的时间一定也相同。第二次小红先走了4分钟,所以接下来,小红与小强相遇所用的时间比第一次少4分钟。
继续观察线段图,小强两次走的路程相同,但由于第二次加快了速度,所以第二次走的时间比第一次少4分钟。根据两次走的路程相同,可以想到数量关系:小强第一次走的速度×时间=小强第二次走的速度×(时间-4)。设第一次相遇用了x分钟,可以列出方程70x-90×(x-4),解得x=18。两人第一次相遇时走了18分钟,所以两家的距离就是(52+70)×18=2196(米)。
有了线段图,我才发现其中的等量关系,线段图帮我顺利解决了问题。
(指导教师 蔡冬健)
猜你喜欢
发明与创新·小学生(2018年12期)2018-12-29
发明与创新·小学生(2018年12期)2018-12-29
今古传奇·故事版(2016年24期)2017-02-07
军事文摘·科学少年(2016年9期)2016-11-03
小学生·新读写(2015年11期)2015-11-20
数学大世界·小学低年级辅导版(2010年2期)2010-03-03
都市家教·上半月(2009年7期)2009-07-13
现代计算机(2009年10期)2009-02-23
故事作文·高年级(2009年2期)2009-02-23
小哥白尼·趣味科学画报(2006年19期)2006-07-11

