基于早期信息和完成信息的项目活动重叠不确定性研究

李南 刘天立

( 南京航空航天大学经济与管理学院，江苏 南京 210016)

0 引言

激烈的市场竞争使生产企业比以往任何时候都迫切需要快速开发出高质量的新产品。活动重叠是交叉并行的活动过程，是缩短项目工期的重要手段。Eppinger 和Krishnan 提出信息的流动一般是有顺序的，上游活动产生早期信息和完成信息，然后将上游信息传输给下游活动［1-2］。活动重叠的实现很大程度上取决于信息变化发生的早晚。信息变化发生得较早，活动重叠导致的返工风险较小，这样的活动重叠才有价值。为了实现顺序活动重叠，Krishnan 和Eppinger 将交流的信息分为早期信息和完成信息两种形式，并据此阐释了活动重叠迭代、优先活动重叠、分裂活动重叠和分散活动重叠四种活动重叠形式［1］。为了更完整描述活动之间的并行性，Eppinger 提出用重叠迭代模型来描述活动之间的并行关系［3］。

由于信息的交流时间难以衡量，以及活动重叠时间的不确定性，Qian Shi 等引进了模糊设计结构矩阵的概念来处理信息交流时间和活动重叠时间，但没有考虑活动重叠导致的返工［5］。白思俊等在DSM 基础上针对信息交流时间及信息传输持续时间等不确定性的问题，提出了“时间因子”的计算项目完工期，但也没有考虑活动重叠导致的返工。设计结构矩阵(DSM)能清晰地描述活动之间的信息交流关系，并以矩阵的形式有效地反映活动间的重叠迭代以及返工［5-6］。在“时间因子”的基础上，杨青等基于顺序活动重叠和反馈活动重叠，研究这两种重叠对返工的影响，并实现工期的优化［7-8］。

根据以上分析，发现现有研究的主要的不足在于以下两点:

(1)没有分析活动重叠的可实现性，即有价值的活动重叠是需要满足一些要求的。首先，只有分析了重叠的可实现性，才能更清晰地找到返工风险的诱因，以达到更好地控制返工风险，降低活动重叠的不确定性的目的。其次，实现有意义的重叠是需要满足一定条件，比如活动间存在强依赖关系不适合实现重叠，如果强制重叠，将会导致进度拖延，费用超支。因此，分析重叠的可实现性，既符合项目现实，也能有效控制返工风险和活动重叠的不确定性，为进一步研究重叠对返工风险、项目工期等影响提供基础。

(2)研究的重点是项目工期优化，忽略了项目成本和质量因素，将会割裂质量、成本与进度的联系。项目进度、成本和质量是相互影响的，不恰当的赶工和重叠迭代，这将会导致成本的失控，并影响工程质量［9］。因此，有必要对进度、成本和质量进行综合研究。

本研究采用早期信息和完成信息来描述活动的重叠可实现性及活动重叠对返工时间的影响，并构建工期和质量损失计算模型，最终通过算例验证了模型的有效性，优化了项目工期。

1 基于信息流的活动重叠描述

1.1 信息流的分类

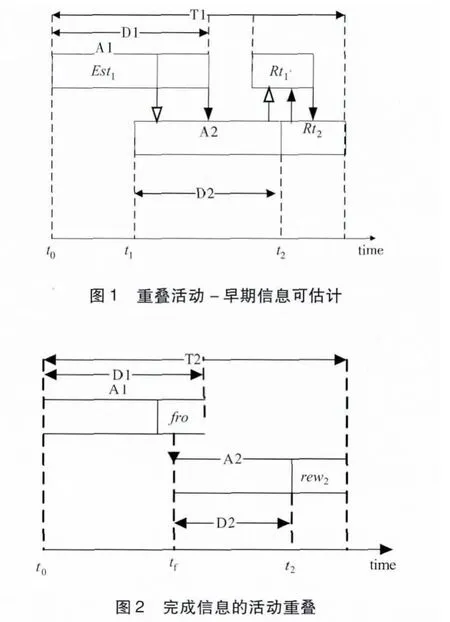
项目执行过程中存在的主要问题是信息缺乏和没有及时地传递足够的信息给下游活动，这会导致混乱无序的项目状态以及加长项目长度［4］。Eppinger 和Krishnan 提出的早期信息是指可以被提早估计的上游信息，完成信息是指上游活动赶工提早完工的信息。如图1 所示，空心箭头表示早期信息流动，实心箭头表示完成信息流动。及时的信息交流是减少活动重叠不确定性的有效方式，并能降低返工风险［10］。

1.2 描述实现活动重叠的方式

传统项目管理认为，只有上游活动结束后，才能将信息传输给下游活动，即传统的顺序作业，即完成-开始关系。在Eppinger 和Krishnan的早期信息和完成信息的基础上，提出了早期信息的活动重叠、完成信息的活动重叠等两种实现重叠的方式。早期信息的活动重叠是指上游的信息可以被提早估计并传输给下游活动，如图1 中的空心箭头所示。完成信息的活动重叠是指上游活动赶工提早完工将完成信息传输给下游活动，如图1 和图2 中实心箭头所示。另外，在图1中，活动A1 向活动A2 输出信息时的空心箭头的位置是指活动A1 的早期信息在活动A2 执行一段时间后传输的，或者是接收到早期信息后A2 才开始执行的。在图2 中，活动A1 向活动A2 输出信息时的实心箭头的位置是指活动A1 的完成信息在活动A2 执行一段时间后传输的，或者是接收到完成信息活动A2 才开始执行的。图1 和图2中参数的含义:Est1为估计早期信息的时间，Rt1为上游活动A1 的返工时间，Rt2为下游活动A2的返工时间，fro 为活动A1 的赶工时间，rew2为完成信息的活动重叠情况下下游活动A2 返工时间。

2 设计结构矩阵(DSM)描述活动重叠

活动重叠的主要意义在于缩短项目工期，但缩短的工期并不等于重叠时间，其原因在于下游活动的持续时间会因重叠而发生变化［11］。当上游的信息被提早估计并传输给下游活动时，产生的早期信息与真实信息可能存在偏差，下游活动将以返工的形式修正此偏差。当上游活动赶工提早完工将完成信息传输给下游活动时，上游活动因赶工失去了应对后续变化的灵活性，导致上游活动出现质量损失［1］。

本研究在杨青等提出的DSM 信息输出和输入时间因子矩阵及返工风险矩阵［12］的基础上，提出了早期信息流输出矩阵O1，输入矩阵I1;完成信息流输出矩阵O2，输入矩阵I2，在信息分类基础上更细致地描绘了重叠对返工的影响情况，用返工概率矩阵RP 和返工时间百分比矩阵RI 来描述重叠导致的返工风险。

3 活动重叠的返工时间、工期、成本以及质量损失的计算

3.1 活动重叠的返工时间

3.1.1 早期信息活动的重叠导致的返工时间

上游活动开始Est1时间后，产生早期信息并传递给下游活动。由于估计信息与真实信息存在偏差，将导致下游活动返工。因此，下游活动的返工时间(如图1 中Rt1部分)为

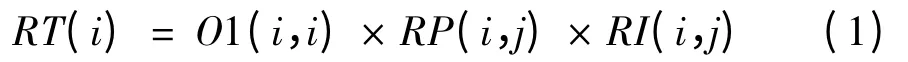
上游活动的返工时间(如图1 中Rt2部分)为

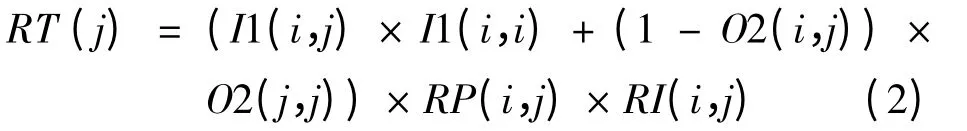
而整个项目的返工时间为

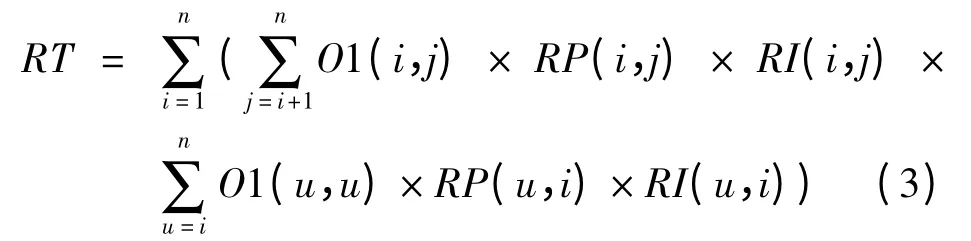
式中，O1(i，j)表示活动j 将早期信息输出给活动i 时活动j 开始的时间因子，I1(i，j)表示活动j 将早期信息输出给活动i 时活动i 开始的时间因子;同样地，O2(i，j)表示活动j 将完成信息输出给活动i 时活动j 开始的时间因子，I2(i，j)表示活动j将完成信息输出给活动i 时活动i 开始的时间因子，RP(i，j)表示活动j 引起活动i 的返工概率，RI(i，j)表示活动j 引起活动i 的返工时间的百分比。

3.1.2 完成信息的活动重叠导致的返工时间

上游活动赶工提早完工fro 时间，产生完成信息传输给下游活动，上游活动由于赶工失去了应对后续变化的灵活性，导致上游活动的质量损失以及下游活动返工。因此，下游活动的返工时间(如图2 中rew2部分)为

根据田口质量损失，上游活动的质量损失(Quality Loss)为

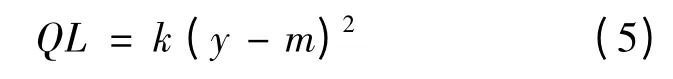
式中，k 为质量损失成本，y 为实际值，m 为目标值，即(y -m)为赶工时间，则上游活动因赶工导致的质量损失为

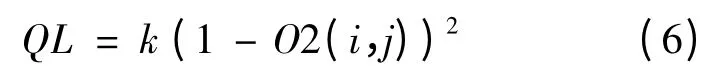
3.2 活动重叠的项目工期计算

用ES 和EF 表示活动的最早开始时间和最早结束时间，i ∈［1，n］，j ∈［1，n］∩，i ≠j，则

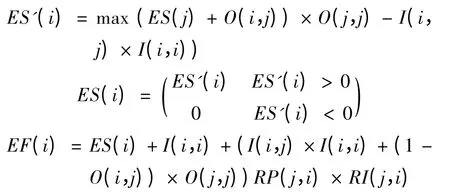
项目工期为

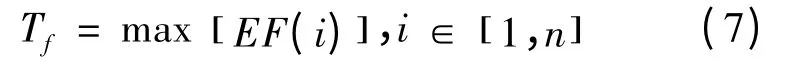
3.3 目标函数

假设某项目的工期计划要求不超过200 天，每天的平均成本为p 元/天，则(200 - Tf)× p 表示工期缩短减少的费用。由于工期和返工的目标函数存在着交叉的部分，因此目标函数在考虑工期的情况下再单独考虑返工时间。

根据式(7)和式(5)，得到基于重叠的成本优化函数为

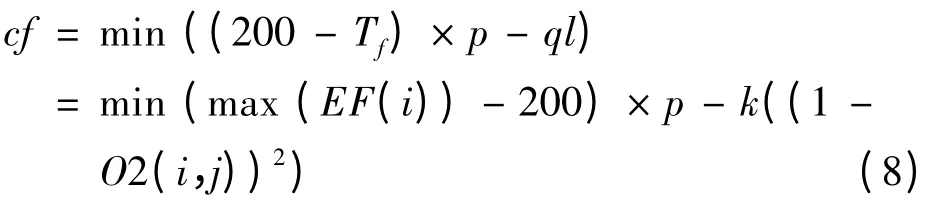
3.4 遗传算法求解项目工期

n 项活动排序优化属于组合优化问题，基于遗传算法在解决组合问题的突出能力，因此，采用遗传算法研究重叠和非重叠情况下对工期、返工、质量损失的影响以及优化活动排序。

3.4.1 编码方式

在解决n 项活动排序优化的问题上，由于二进制编码采用0 或1 编码，无法表示项目活动的工序顺序，而n 进制编码采用活动顺序［1，2，…，n］编码，任何一个活动顺序都是一个可行解，因此在n 项活动排序优化问题上，n 进制编码比二进制编码更有效。另外，n 进制编码基因码长度为n，每个编码位取值为［1，n］的整数，且每一个编码位的整数都不相同， ［1，n］的每一个整数当且仅能出现在某一个编码位上。例如，当n =6 时，一个染色体编码［2 -5 -1 -3 -6 -4］，父代1 在DSM 中表示从上到下的执行顺序，或者从上游活动到下游活动的执行顺序(图3)。

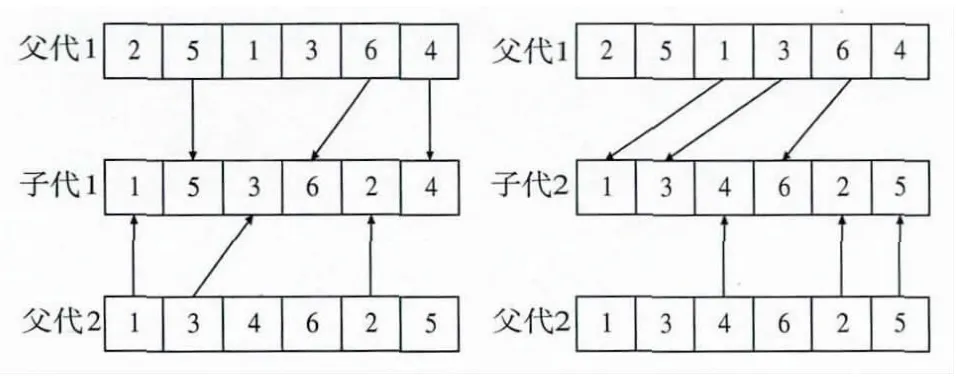
图3 交叉图

3.4.2 适应度函数

适应度函数一般是求最大值，因此取式(8)作为目标函数，即fitness(x)= cf。

3.4.3 遗传算子

选择与交叉算子:采用轮盘赌选择方法，多点交叉算子交叉运算(图3)。

变异算子:采用多点变异算子，将活动序号随机交换，生成下一代个体(图4)。

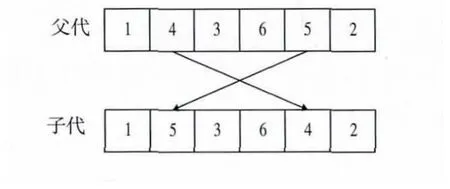
图4 变异图

3.4.4 最优保留策略

为了加快收敛速度，本研究采取最优个体保留策略，将每一代中的最优个体保存入下一代，并且不参与选择、交叉和变异操作，直到有更好的个体代替它为止。

3.4.5 停止准则

当适应度函数值达到要求或超过最大迭代次数后停止。

4 算例

4.1 算例背景

本研究算例取自杨青、黄建美《基于活动重叠的DSM 项目时间计算及排序优化》一文中的案例作为算例分析。该算例由13 项活动组成，根据以上对于早期信息和完成信息的分析，将原文中的输出时间因子矩阵O 分为矩阵O1 和O2，依据是矩阵O 中非对角线的值小于0.9 的所有活动时间因子值归入矩阵O1，其他不小于0.9 的所有活动时间因子值归入矩阵O2。根据矩阵O1和O2 将原文中矩阵I 分成矩阵I1 和I2。返工概率矩阵RP 是原文中矩阵RP，返工时间百分比矩阵RI 是原文中矩阵RI。

4.2 目标函数求解及优化结果分析

本研究在遗传算法中的参数设置为:遗传种群为26 种;遗传代数为300;交叉概率pc=0.8;变异概率pm =0.05。从不考虑重叠的顺序作业状态、项目工期最小化下的顺序作业状态、早期信息流重叠状态、完成信息流重叠的状态四个方面来研究目标函数优化问题，相应求解过程如下，具体结果如表1 所示。

(1)在不考虑重叠的情况下，以项目工期最小化为目标函数优化项目进度。将原文中的矩阵O，除了对角线中数值不变，其余数值均取1，矩阵I，除了对角线中数值不变，其余数值均取0(图7)。

(2)在考虑重叠情况下，以式(8)为目标函数进行优化，采用上述提到的遗传算法。在前20 代内，发现在10 代左右最优适应度值开始收敛，表明算法稳定性好(图5)。

根据表1 分析得出以下结论:

表1 项目初始状态及两种重叠状态计算结果对比

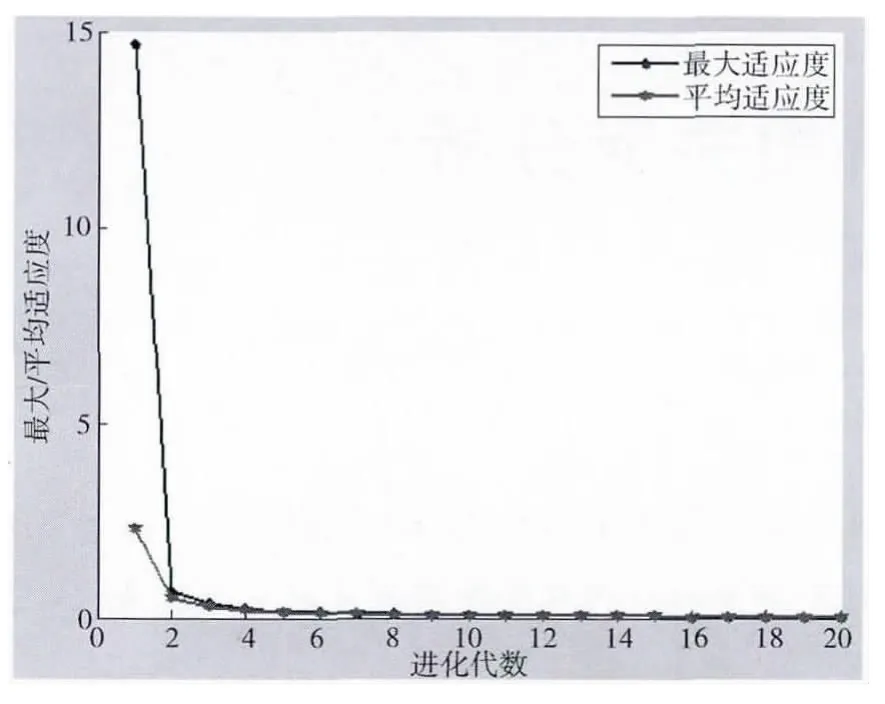
图5 适应度变化趋势图

(1)在以项目工期最小化为目标函数时，早期信息流重叠的项目工期比顺序作业状态项目工期缩短12.14%，完成信息重叠流的项目工期比顺序作业状态项目工期缩短15.57%，与不考虑项目工期最小化的顺序作业初始状态都有明显的优化。从优化前的DSM 和优化后的DSM 可以看出，虽然优化了项目工期，但对于上三角的反馈个数并未减少，或者还有增多的趋势，这也表明了反馈个数并不是越少越好［13］。

(2)与完成信息流重叠对比发现，早期信息流重叠显然加大了返工风险，返工时间比较长，并且早期信息流重叠的项目工期相对比较长，则完成信息流重叠对项目工期可能更为优化，但还要考虑完成信息导致的质量损失成本。

(3)完成信息重叠时产生的质量损失取决于质量损失成本k 的大小，k 越大，质量损失成本就越高，在权衡工期缩短成本和质量损失之间大小也和k 有关，因此早期信息流重叠和完成信息流重叠有效性还取决于质量损失成本k 的大小。

(4)由表1 以及式(8)分析得出，0 ≤k ≤0.14 × p 时，完成信息流重叠优于早期信息流重叠对于项目工期的优化;0.14 ×p ＜k ≤0.49 ×p，早期信息流重叠优于完成信息流重叠对于项目工期的优化;k ＞0.49 ×p，顺序作业状态优于完成信息流重叠对于项目工期的优化。

5 结语

从信息流角度分析了重叠可实现性，并提出了实现重叠的两种方式，并结合返工风险、质量损失、工期，从成本的角度进行优化，得到相应的活动顺序和工期优化。对信息流的细分、早期信息流重叠和完成信息流重叠的影响研究，更细致地展现信息流间的区别，更透彻地分析信息流对工期、返工风险以及质量损失的影响，以便采取相应的方式方法应对风险。

［1］ Viswanathan Krishnan，Steven D Eppinger，Daniel E Whitney.A model-based framework to overlap product development activities［J］.Management Sciences，1997，43 (4):1103-1108.

［2］ Krishnan V，Ulrich K T.Product development decisions:A review of the literature ［J］.Management Science ，2001，47 (1):1-21.

［3］ Robert P Smith，Steven D Eppinger. A Predictive Model of Sequential Iteration in Engineering Design ［J］ . Management Science，1997，43 (8):1104.

［4］ D K H Chua，Aslam Hossain.A simulation model to study the impact of early information on design duration and redesign ［J］.International Journal of Project Management，2011，29 (7):246-257.

［5］ Qian Shi，Tomas Blomquist.A new approach for project scheduling using fuzzy dependency structure matrix ［J］. International Journal of Project Management，2013，32 (4):503-510.

［6］ Steward D V，The Design Structure System:A Method for Managing the Design of Complex Systems ［J］，IEEE Transactions on Engineering Management，1981，28 (3):71-74.

［7］ 白思俊，万小兵. 基于设计结构矩阵的项目进度周期［J］.系统工程理论与实践，2008 (11):38-41.

［8］ 杨青，黄建美. 基于活动重叠的DSM 项目时间计算及排序优化［J］. 系统工程理论与实践，2011 (3):496-504.

［9］ 徐玉凤，董亚辉. 项目进度管理［M］. 北京:对外经济贸易大学出版社，2007.

［10］ Issam M Srour，Mohamed-Asem U Abdul-Malak，Ali A Yassine，et al.A methodology for scheduling overlapped design activities based on dependency information ［J］. Automation in Construction，2013，29 (1):1-11.

［11］ Jun Lin，Kah Hin Chai，Aarnout C Brombacher，et al.Optimal overlapping and functional interaction in product development［J］. European Journal of Operational Research.2009，196(3):1158-1169.

［12］ 杨青，吕杰峰. 基于DSM 返工风险评价矩阵的项目优化与仿真［J］. 系统工程理论与实践，2010 (9):1665-1671.

［13］ Browning T R. Applying the Design Structure Matrix to System Decomposition and Integration Problems:A Review and New Directions ［J］. IEEE Transactions on Engineering，2002，48(3):292-306. PMT