短延迟多径干扰下的跟踪环路鉴别器设计

同 钊,李兵兵,惠永涛,钟兴旺,刘 浩

(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.中国空间技术研究院西安分院,陕西西安 710100)

短延迟多径干扰下的跟踪环路鉴别器设计

同 钊1,李兵兵1,惠永涛1,钟兴旺2,刘 浩1

(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.中国空间技术研究院西安分院,陕西西安 710100)

针对短延迟多径干扰影响下传统多径消除方法性能下降的问题,提出了一种跟踪环路鉴别器的构造方法.首先分析了短延迟多径下同相/正交超前、滞后与即时支路的输出特性,在此基础上构建出一种改进的超前支路;将环路鉴别器的输出定义为归一化超前减滞后功率型函数,从而使得直达信号码相位与本地估计码相位的误差小于预设门限值.理论分析和仿真结果表明,与传统多径抑制方法相比,基于改进环路鉴别器的多径抑制技术,能够减小相对时延小于0.5码片时多径带来的码跟踪误差,有效抑制了短延迟多径干扰,进而提高了导航与对接系统中的跟踪测量精度.

码跟踪环路;鉴别器;多径;跟踪测量精度

多径效应是影响卫星导航与空间交会对接系统测距精度的重要误差来源[1].由于传输信道中存在遮挡物,测距信号通过非视线(Line Of Sight,LOS)路径到达接收机,导致接收机天线收到从多条路径传来的电波信号,使得原始测距信号在相位、幅度和延迟上发生变化,进而影响测量精度.多径效应引起的伪码和载波相位偏差依赖于接收机的周围环境,在空间上的相关性较小,难以通过差分方法进行消除[2].因此,研究多径误差消除技术对提高导航定位准确性和对接成功率具有重要意义.

为了消除多径影响,国内外学者提出了各种多径抑制技术,主要分为改进接收机天线结构和改进接收机信号处理技术两类[3]:第1类方法通过改进天线结构,使得方向图的主瓣对准测距信号的来波方向,减少对多径反射方向信号的接收.该方法通常需要已知或估计发射端的角度信息,具有一定的局限性;第2类方法在基带信号处理层面上又分为参量式与非参量式两类[4].参量式多径消除算法的核心是对直达信号和多径信号的多个参数进行有效的估计,如多径估计延迟锁定环(Multipath Estimating Delay Lock Loop, MEDLL)方法[5]和基于最大似然估计的多径抑制技术(Multipath Mitigation Technique,MMT)[6],此类方法需要较高的采样频率和较多的相关器,计算复杂度高,且只适用于多径环境相对固定的场景.非参量式方法通过设计合理的码鉴别器来减小多径带来的码跟踪误差,由于其性能稳定、抑制效果较好而受到了广泛的关注[7].其典型代表是窄相关技术[8],该技术通过减小传统相关器中早和迟相关器的间隔来抑制多径,将相关能量集中于信号的上升沿和下降沿,对中长延迟多径的抑制效果明显.为了保持自相关函数峰值的三角形状以维持码环的敏感性,窄相关器的接收机必须采用较宽的射频前端滤波器带宽,从而使得更多的噪声和干扰信号进入跟踪环路.相关学者后续对窄相关技术进行了改进,分别提出了超前滞后斜率(Early Late Slope,ELS)技术和双-Delta(Double-Delta)技术,其中,ELS技术利用相关峰两侧的坡度实现对直达信号的跟踪,虽然与窄相关技术相比,其性能有所改善,但在计算跟踪误差时存在除法操作,限制了误差修正在硬件中的可实现性;Double-Delta技术基于相关函数相关峰附近受多径干扰较少这一特点,利用两组分布在相关峰附近的相关器输出组合成鉴相函数,增强对多径信号的抑制能力,更易于硬件集成,其实现形式有高分辨率相关器(High Resolution Correlator,HRC)[9]技术和闸门相关器(Strobe Correlator)[10]技术等.但是与窄相关技术相比,Double-Delta技术对短延迟多径抑制性能的提升并不明显.

我国北斗卫星导航系统已开始向用户提供导航服务[11],然而其卫星监控网络在海外布站存在较大困难,需要通过星间链路测量进行自主导航.同时,空间交会对接系统也需要通过星间精密测距,获得运动中载体的瞬时位置、航行速度和载体姿态等参数.此类星间测量过程中产生的多径信号延迟小、幅度强,并且与直达信号之间具有较大的相关性.现有的高精度卫星测距系统对测距精度的要求达到了10μm级.以上传统多径消除方法对于中长延迟多径具有明显的抑制效果,但将其应用到短延迟多径场景下则无法满足高精度测量需求[12].目前关于短延迟多径消除技术的研究较少,文献[13]采用最小二乘(Least Square,LS)方法对短延迟多径参数进行估计,根据估计值提出了差分和均衡滤波两种多径消除方法.该方法虽然实现简单,但存在噪声放大的缺陷.为了克服短延迟多径干扰下传统多径抑制方法性能下降的问题,笔者提出了一种短延迟多径消除(Short-delay Multipath Eliminating,SME)的环路鉴别器构造方法.该方法首先对多径时延小于1/2相关器间隔情况下的同相/正交超前、滞后与即时支路的输出进行理论推导,并在此基础上构建出一种改进的超前支路;将环路鉴别器的输出定义为归一化超前减滞后功率型函数,使得鉴别器输出曲线的过零点偏移控制在允许误差范围内,从而降低直达信号的跟踪误差,有效抑制短延迟多径干扰.

1 多径信号模型

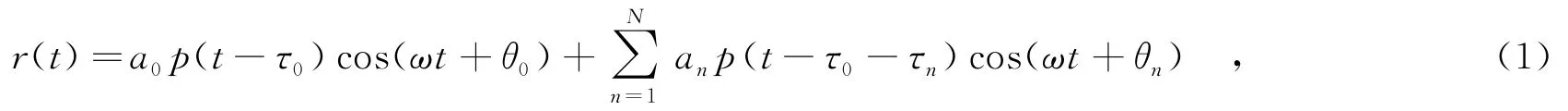
其中,a0为直达信号幅度,p(t)表示测距采用的C/A码波形,ω为载波频率,τ0和θ0分别为直达信号到达接收机时的时间延迟和载波相位,N为多径条数,an为第n条多径的幅度,τn和θn分别表示第n条多径相对于直达信号的时延和载波相位.假设本地载波能够正确跟踪接收信号的频率,本地产生的对准信号为cos(ωt+和其中,为估计的载波相位,为估计的码相位延迟.将接收信号与本地

多径信号可分为反射多径和散射多径两种类型.对于反射多径,可模拟为1路或几路伪随机码调制信号的延迟信号;而散射多径则是很多延迟的接收信号之和,往往表现为一个附加的噪声通道,对伪码跟踪和伪距测量的影响很小[14].因此,研究接收机抗多径性能时需要产生的多径信号主要是镜面反射多径.

在不考虑噪声的情况下,接收机接收到的信号模型为

对准信号进行相关运算,可得即时同相与正交支路的输出分别为

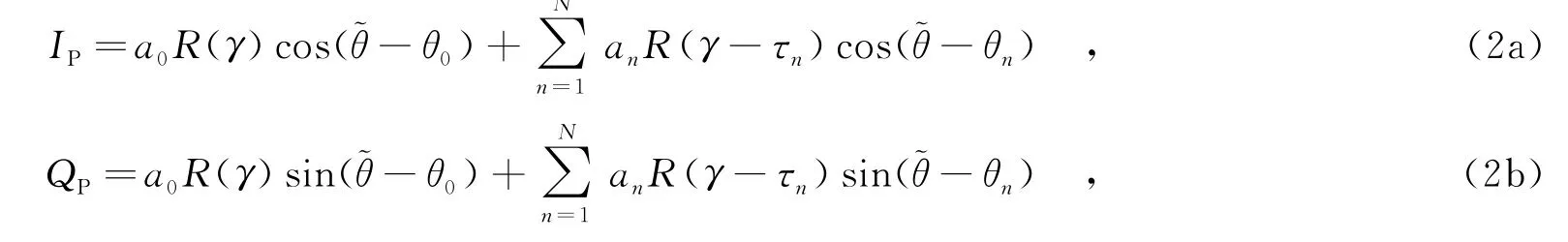
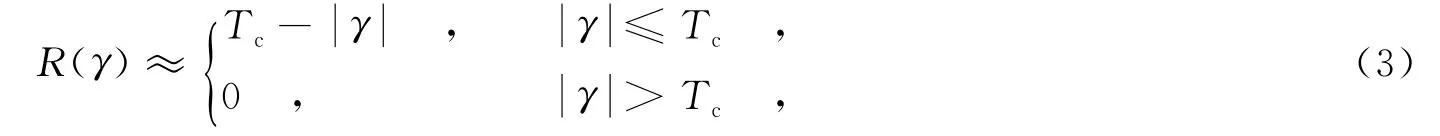
其中,Tc为一个码片的时间宽度.取相关器间隔为d(其中d≤Tc),对式(2)中的自相关函数分别超前和滞后d/2,可得同相/正交超前与滞后支路的输出,可表示为

传统鉴别器算法包括相干型码鉴别器、点积功率型码鉴别器和包络型码鉴别器等.可以证明,以上鉴别器当输出为零时,时延估计误差均不为零,这说明存在多径误差.当多径时延大于码片周期Tc时,测距码可以通过其自相关特性消除多径干扰.对于小于Tc的中长时延多径,可通过减小早迟相关器的间隔,得到较好的抑制性能.但是不断缩小相关器间隔,并不能完全抑制0.5Tc内的短延迟多径信号.

2 新的环路鉴别器构造方法及码环更新过程

为解决短延迟多径干扰问题,需要对多径时延和码相位误差在相关器范围内时,即0＜τn≤d/2,时,对各个支路的输出进行分析.通过对同相超前与滞后支路进行分析,可得

同理,可计算出正交超前与滞后支路之和为

在式(4)和式(5)的基础上,构建一种包含最大时延信息的超前支路为

将SME环路鉴别器的输出定义为归一化超前减滞后功率型函数,即

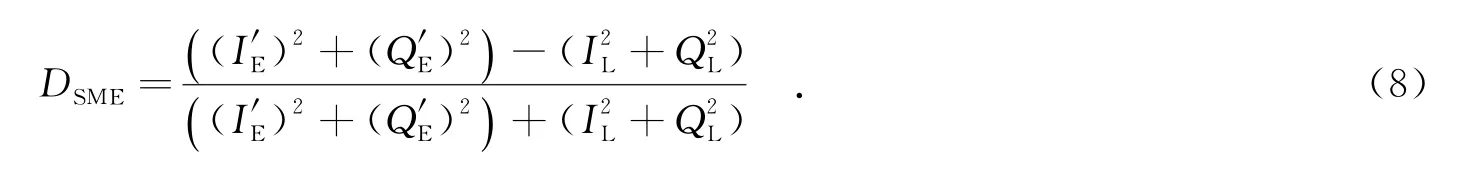
式(8)中的鉴别器同时利用了I和Q支路,能获得较大的动态范围.同时,引入归一化操作,去除了对接收信号幅度的敏感性,环路跟踪的牵引范围变大,从而对接收信号的幅度抖动具有更强的鲁棒性.

假设只存在一条多径链路,则SME环路鉴别器输出分析如下.

当γ＜0,0＜τ1≤d/2时,即时支路信号的码相位超前于直达信号的码相位,如图1(a)所示.利用测距码的自相关函数特性,式(6)和式(7)可表示为

此时超前支路与滞后支路的输出相同,则由式(8)可得鉴别器函数输出DSME_1=0.

当0≤γ＜τ1≤d/2时,即时支路信号的码相位处于直达信号和多径信号的相位之间,如图1(b)所示.利用测距码的自相关函数特性,改进的超前支路可表示为

图1 直达信号、多径信号和复合信号相关函数的位置关系

将式(10a)与式(10b)代入式(8),可得SME环路鉴别器的输出为

其中,

当0＜τ1≤γ≤d/2时,即时支路信号的码相位处于滞后信号与多径信号的相位之间,如图1(c)所示.利用测距码的自相关函数特性,改进超前支路的表达式为

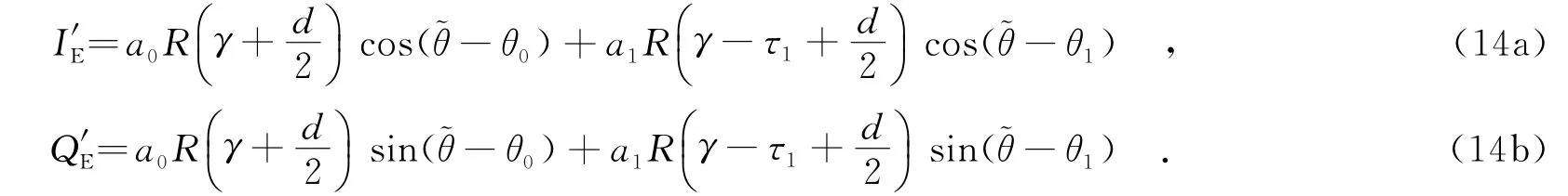
将式(14)代入式(8),可得SME环路鉴别器的输出为

其中,

通过对以上3种情况下SME环路鉴别器输出表达式的推导,可以证明,当-d/2≤γ≤0时,鉴别器输出为0;当γ＞0时,鉴别器输出为负值,并且在任意一点连续.图2给出了相关器间距d=1码片,多径直达信号比(Multipath Direct Ration,MDR)a1a0=0.5,多径信号相位延迟τ1=0.15码片,相位差分别取π/6和5π/6时,传统窄相关鉴别器和所提出的SME环路鉴别器的输出曲线.从图2可以看出,SME鉴别器的输出与以上理论分析相符合,当码环鉴别器输出为零时,伪码相位误差γ=0;同时也验证了传统鉴别器函数的过零点偏移现象,即鉴别器输出为零时,γ≠0.

根据SME环路鉴别器的输出特性,相应的码环更新过程设计如下:在码环跟踪初始阶段,首先对接收到的信号进行码相位估计,并得到此时的鉴别器输出;若鉴别器输出DSME＜0,则按照初始步长λ向左移动

图2 鉴相器的输出曲线

本地参考信号,直至DSME=0,此时将步长减半,并向右移动本地参考信号,直至DSME＜0.以此类推,缩减步长直到小于预设误差门限η;若鉴别器输出DSME=0,则以λ为初始步长向右移动本地参考信号直至DSME＜0,然后按照DSME＜0时的更新过程进行码环更新.由以上码环更新过程可知,SME环路鉴别器对准时的零点偏移小于预设误差门限η,从而将即时支路与直达信号间的相位差控制在预设范围内,有效抑制了时延小于d/2的多径干扰.

3 数值仿真及复杂度分析

为了验证文中提出的SME鉴别器的多径抑制性能,下面将对其进行仿真,并与MEDLL[5]、Doubledelta[10]和LS[13]等多径抑制方法的性能进行比较.考虑只存在一条多径信号,则MDR为0.5,测距码频率为1.023 MHz,载波频率为1 575.42 MHz,采样频率为4 MHz,接收机带宽为6 MHz,载波相位差为5π/6,相关器初始间隔设置为d=1码片,预设误差门限为η=10-4码片,成型和匹配脉冲采用均方根升余弦滤波器.

图3对无噪声情况下4种多径抑制技术的码跟踪误差包络随多径时延的变化曲线进行了仿真.仿真结果表明,当多径时延大于0.5码片时,0＜τn≤d/2条件下的理论分析不一定成立,从而导致文中方法在环路跟踪稳定时估计误差较大;在多径时延小于0.5码片时,其他3种多径抑制方法性能均不理想,而文中提出的SME鉴别器的误差包络接近于零,从而满足高精度卫星测距系统对测距精度的要求,适用于自主导航与对接等高精度测距系统中的短延迟多径消除.

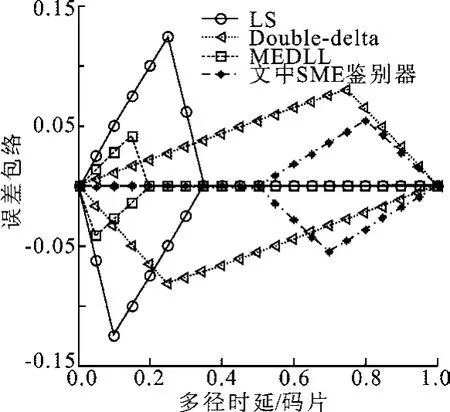
图3 跟踪误差包络随多径时延的变化曲线

图4 不同MDR场景下的跟踪误差包络比较

为研究MDR对不同算法性能的影响,图4分别仿真了MDR为0.3和0.5时,4种多径抑制方法的码跟踪误差包络,为便于观察,只对同相支路多径进行了仿真.仿真结果表明,MEDLL、Double-delta和LS方法受MDR的影响较大,当MDR增大时,多径抑制性能有所下降.而文中提出的SME鉴别器由于进行了幅度归一化操作,使得多径抑制性能不再受MDR的影响,对接收信号的幅度变化具有更强的鲁棒性.

为了验证提出的SME鉴别器受噪声影响时的性能,图5对多径时延为0.1码片时的SME鉴别器与其他3种多径抑制方法,在不同载波噪声比(Carrier-to-Noise Ratio,CNR)下的性能进行了仿真.从仿真结果中可以看出,4种方法的码跟踪误差均随CNR的增大呈减小趋势;当CNR相同时,LS方法由于对噪声项与信道矩阵的伪逆进行了乘积,当信道衰减严重时引起噪声放大,因此跟踪误差最大.文中提出的SME鉴别器在不同CNR情况下的性能均优于其他3种方法,并且当CNR越小时,多径抑制性能的优势越明显.

图5 跟踪误差随载噪比的变化曲线

表1 不同方法的计算复杂度比较

下面对文中提出的SME环路鉴别器方法与现有的LS、Double-delta和MEDLL方法的计算复杂度进行比较.令m=1Tc,环路更新次数为n,采用实数乘法和加法的总操作次数来衡量算法的计算复杂度.不同算法的计算复杂度比较如表1所示.

结合性能比较和表1中的复杂度对比可看出,文中提出的方法与LS、Double-delta方法的计算复杂度相当,比MEDLL方法的计算复杂度更低,且短时延抑制性能较其他方法更好,因而对于存在短时延多径的高精度测距场景具有工程应用价值.

4 结束语

传统多径消除方法对于中长延迟多径具有明显的抑制效果,但将其应用到短延迟多径场景下则无法满足高精度测量需求.针对上述问题,笔者通过分析短延迟多径下同相/正交超前、滞后与即时支路的输出特性,构建出一种改进的超前支路,并将环路鉴别器的输出定义为归一化超前减滞后功率型函数,使得直达信号码相位与本地估计码相位的误差控制在预设范围内.通过理论分析和仿真,验证了新的环路鉴别器能够降低多径时延小于0.5码片的包络误差和码跟踪误差,有效抑制了短延迟多径干扰,对于自主导航与对接系统中的高精度测量场景具有重要的实用意义.

[1]高扬,姚铮,崔晓伟,等.导航接收机跟踪环对多径误差影响的分析[J].华中科技大学学报(自然科学版),2013, 41(10):21-29. Gao Yang,Yao Zheng,Cui Xiaowei,et al.Influence of Tracking Loops in Navigation Receivers on Multipath Error[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2013,41(10):21-29.

[2]李豹,许江宁,曹可劲,等.北斗二代导航信号抗多径性能分析与仿真[J].中国惯性技术学报,2012,20(3):339-342. Li Bao,Xu Jiangning,Cao Kejin,et al.Analysis and Simulation on Anti-multipath Performance of Beidou2 Navigation [J].Journal of Chinese Inertial Technology,2012,20(3):339-342.

[3]王纯,张林让,胡子君.采用阵列天线的GPS接收机的多径抑制方法[J].宇航学报,2014,35(7):843-849. Wang Chun,Zhang Linrang,Hu Zijun.A Multipath Mitigation Method for Array Antenna-based GPS Receiver[J]. Journal of Astronautics,2014,35(7):843-849.

[4]高源,张磊,龙腾.卫星导航信号可变间距采样的多径估计方法[J].华中科技大学学报(自然科学版),2014,42(4): 30-34. Gao Yuan,Zhang Lei,Long Teng.Multipath Estimation Algorithm Using Various Spacing Sampling in Satellite Navigation Signal[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2014, 42(4):30-34.

[5]Sanchez-Fernandez M,Aguilera-Forero M,Garcia-Armada A.Performance Analysis and Parameter Optimization of DLL and MEDLL in Fading Multipath Environments for Next Generation Navigation Receivers[J].IEEE Transactions on Consumer Electronics,2007,53(4):1302-1308.

[6]Fenton P C,Jones J.The Theory and Performance of Novatel Inc.Vision Correlator[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas:Institute of Navigation,2005:2178-2186.

[7]孔德庆,施浒立,胡超.一种基于窄相关器差分的多径误差抑制方法[J].宇航学报,2008,29(6):1834-1839. Kong Deqing,Shi Huli,Hu Chao.A New Method for Multipath Mitigation Based on Difference of Narrow Correlators [J].Journal of Astronautics,2008,29(6):1834-1839.

[8]Betz J W,Kolodziejski K R.Extended Theory of Early-late Code Tracking for a Bandlimited GPS Receiver[J].Journal of Institute of Navigation,2000,47(3):211-226.

[9]McGraw G A,Braasch M S.GNSS Multipath Mitigation Using Gated and High Resolution Correlator Concept[C]// Proceedings of the National Technical Meeting of the Institute of Navigation.California:Institute of Navigation,1999: 333-342.

[10]Garin L,Van Diggelen F,Rousseau J.Strobe and Edge Correlator Multipath Mitigation for Code[C]//Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation.Alexandria:Institute of Navigation,1996:657-664.

[11]刘龙伟,李文刚,李凤娇.卫星导航定位信息辅助的协作波束赋形算法[J].西安电子科技大学学报,2013,40(3):7-13. Liu Longwei,Li Wengang,Li Fengjiao.Cooperative Beamfoming Algorithms Using the Assistant Information from Satellite Navigation Positioning Systems[J].Journal of Xidian University,2013,40(3):7-13.

[12]Zhang Z,Law C L.Short-delay Multipath Mitigation Technique Based on Virtual Multipath[J].IEEE Antennas and Wireless Propagation Letters,2005,4(1):344-348.

[13]Zhang S K,Wang H B,Yang J,et al.GPS Short-delay Multipath Estimation and Mitigation Based on Least Square Method[J].Journal of Systems Engineering and Electronics,2009,20(3):1-9.

[14]张鑫,刘小汇,肖志斌,等.一种低复杂度高精度多路GNSS多径信号模拟方法[J].中南大学学报(自然科学版), 2014,45(1):111-116. Zhang Xin,Liu Xiaohui,Xiao Zhibin,et al.A Low Complexity High-precision Multi-channel GNSS Multipath Signal Simulation Method[J].Journal of Central South University(Science and Technology),2014,45(1):111-116.

(编辑:齐淑娟)

Design of the discriminator for tracking the loop under short-delay multipath interference

TONG Zhao1,LI Bingbing1,HUI Yongtao1,ZHONG Xingwang2,LIU Hao1
(1.State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China; 2.CAST-Xi’an Institute of Space Radio Technology,Xi’an 710100,China)

The traditional multipath eliminating methods have poor performance under short-delay multipath interference and therefore a discriminator constructing method for tracking the loop is presented. Firstly,from the analysis of the output characteristics for in-phase/quadrature-phase early,late,and prompt channels under the short-delay multipath,an improved late channel is constructed.The output of the loop discriminator is defined as the normalized function of the power difference between early and late signals.It made the error between the code phase of the direct signal and that of the local estimated signal is less than the pre-determined threshold.Theoretical analysis and simulation results show that,compared to traditional methods,the multipath mitigation technique based on the improved loop discriminator can suppress the code tracking errors produced by the multipath when the relative delay is less than 0.5 chip and effectively inhibits short-delay multipath interference,thus improving the tracking and measurement accuracy in navigation and docking systems.

code tracking loop;discriminator;multipath;accuracy of tracking and measurement

TN967.1

A

1001-2400(2015)05-0007-06

2014-08-10< class="emphasis_bold">网络出版时间:

时间:2014-12-23

国家自然科学基金资助项目(61271299);中央高校基本科研业务费专项资金资助项目(K5051301034);高等学校学科创新引智计划资助项目(B08038);中国空间技术研究院西安分院航天创新基金资助项目(HX0113011907)

同 钊(1989-),女,西安电子科技大学博士研究生,E-mail:loki_tong@126.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.002.html

10.3969/j.issn.1001-2400.2015.05.002