（2＋1）维Calogero－Bogoyavlenskii－Schiff方程新的精确解

鱼 翔，陈文利

（西安培华学院 基础部，陕西 西安710125）

0 引 言

非线性偏微分方程的求解问题特别是对一些高维的非线性微分方程的求解方法已成为研究的热点.近年来，对非线性偏微分方程寻找对称约化和构造精确解方面的研究取得了很大的进展.为了得到非线性偏微分方程的精确解，研究者提出了很多方法，诸如经典的李群方法［1］，非经典的李群方法［2］，CK直接法［3］和改进的CK直接法［4－6］.并且利用改进的CK直接法已经获得了很多非线性偏微分方程的一般对称群和精确解.

文献［7－8］研究（2＋1）维 Calogero－Bogoyavlenskii－Schiff（CBS）方程，利用 Hirota双线性法求出了CBS方程的部分多孤子解；文献［9］利用经典的李对称方法给出了CBS方程的李点对称；文献［10］给出了（2＋1）维广义CBS方程的无穷多对称及其约化；文献［11］利用李群分析法和行波约化法给出了（2＋1）维CBS方程的相似解；文献［12］利用拓展的双曲函数展开法求出了该方程的行波解.改进的CK直接从最一般的相似约化出发，不使用群理论，就可以得到用标准李群方法得不到的解.本文利用改进的CK直接法求解（2＋1）维CBS方程的一般对称群和新的精确解，并建立了新解和旧解的联系，得到了该方程一些新的精确解.

1 （2＋1）维CBS方程的对称群

（2＋1）维CBS方程的一般形式

假设方程（1）具有如下形式的对称群

其中，r＝r（x，z，t），s＝s（x，z，t），f＝f（x，z，t），g＝g（x，z，t），h＝h（x，z，t）都是关于x，z，t的待定函数.这些待定函数可以通过U（f，g，h）变换｛u，x，z，t｝→ ｛U，f，g，h｝下要求U（f，g，h）满足方程

来确定.

根据改进的CK直接法，寻求方程（1）的一般对称群和新的精确解.将方程（2）代入方程（1）得到

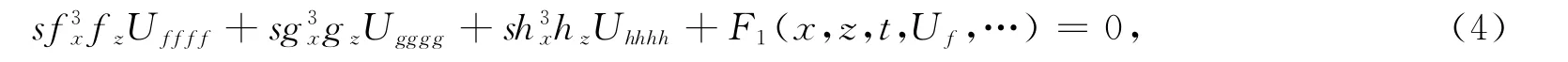
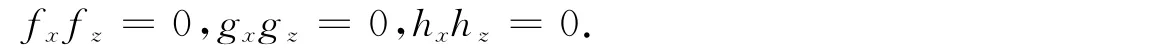
如果fx＝0，方程（1）没有非平凡解，所以有

将方程（5）代入方程（3）可以得到

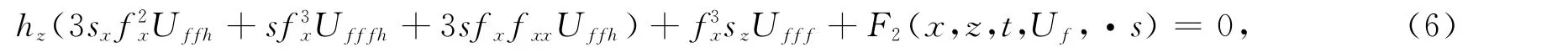
其中，函数F（x，z，t，Uf，…）与无关.由方程（6）可以得到

按照上述方法进行计算便可得到决定方程组

解方程组（7）可以求解出待定函数

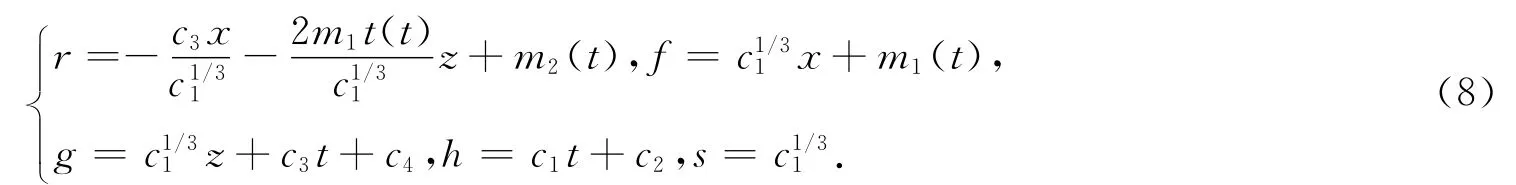
其中，c1，c2，c3，c4均为常数，m1（t），m2（t）为t的任意函数.根据方程（2）有

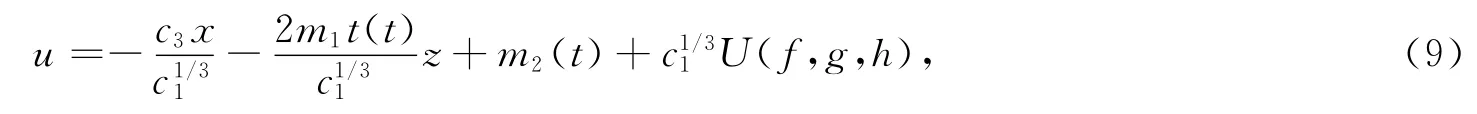
其中，f，g，h由方程（8）确定.由方程（8）和（9）并根据（2＋1）维CBS方程的对称群理论，有如下的对称群定理.

定理1 当U（x，z，t）是方程（1）的解时，由式（9）所表达的u也是方程（1）的一个解.

根据定理1，方程（9）给出的对称群为Lie点对称群.通过代换讨论其Lie代数.

其中，ε为无穷小参数；p1（t），p2（t）为t的任意函数，则方程（9）为

其中

2 （2＋1）维CBS方程的精确解

为了得到方程（1）的约化方程，利用σ＝0和方程（1）的相容性.首先求解σ＝0时方程（1）的特征方程组

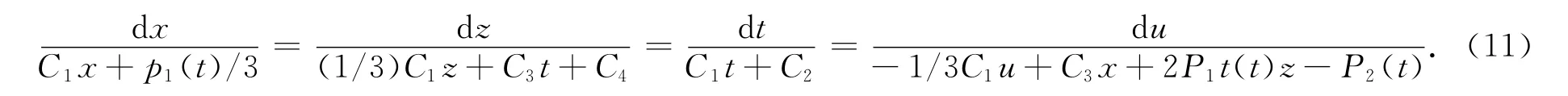
现在讨论以下几种情况：

情况（Ⅰ）：令

通过求解特征方程组可以得到其不变解为

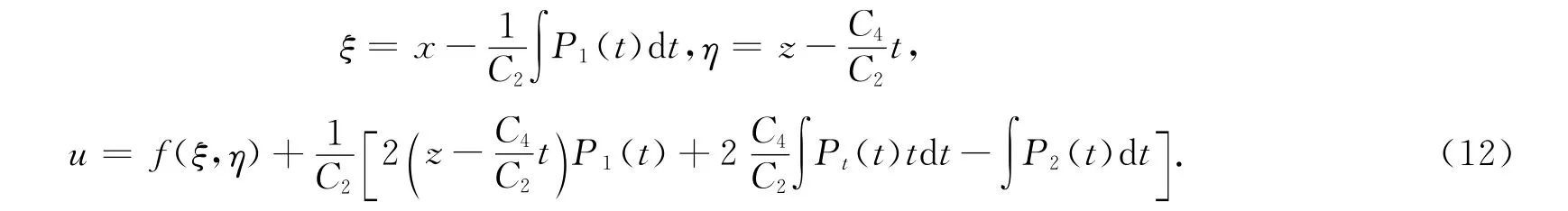
将方程（12）代入方程（1）可得到约化方程为

令z＝kξ＋lη.其中k，l为非零常数.则方程（13）可以写为

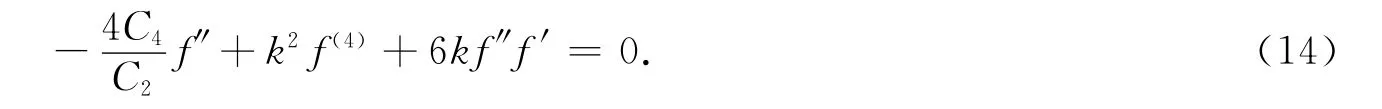
由齐次平衡原则可知n＝1.因此假设方程（14）有如下形式的解

其中，φ为Riccati方程φ′＝A＋φ2的解，将方程（15）代入方程（14）并且令φi的系数都为0，可以得到关于bi的一个代数系统.求解可知

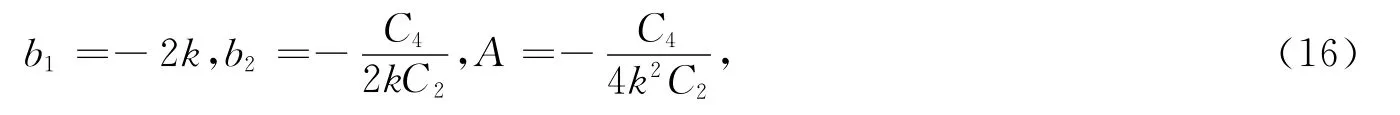
其中，b0为任意常数.

当A＜0时，方程（14）的精确解为

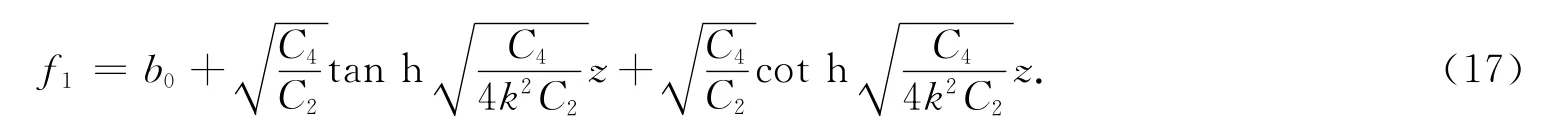
当A＞0时，方程（14）的精确解为

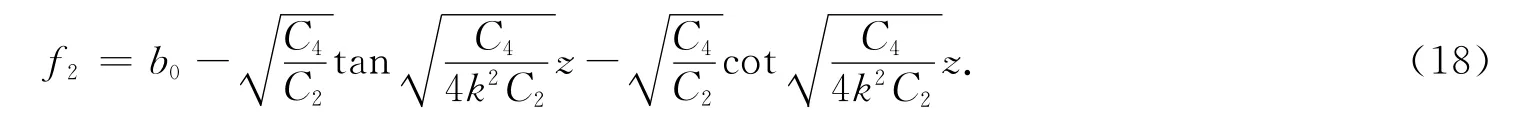
由方程（14），（15）和fi（i＝1，2）可以得到方程（1）的新精确解

情况（Ⅱ）：令C1＝C2＝C3＝0，C4≠0，P1（t）＝a，P2（t）＝b同样的方法可以得到不变解为

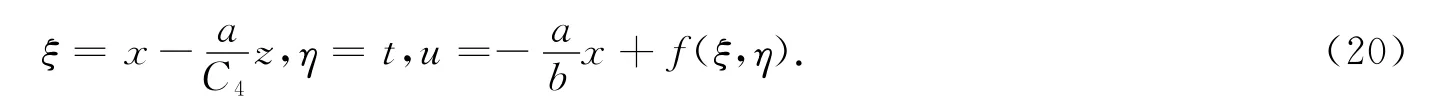
将方程（20）代入方程（1）可得

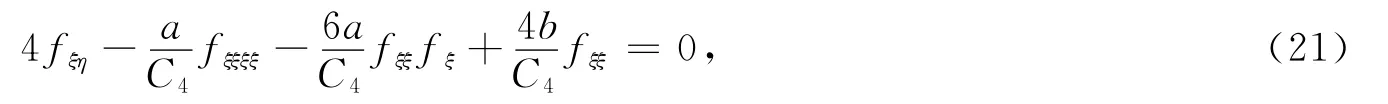
令z＝kξ＋lη.其中k，l为非零常数.则方程（21）可以写成

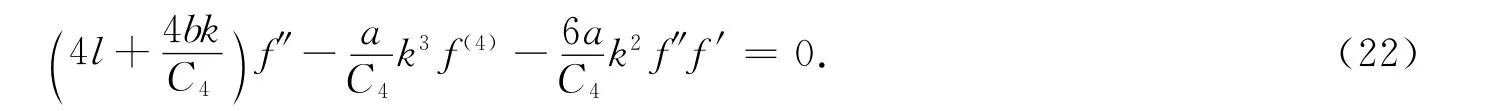
利用G′／G方法求解方程（23）.假设方程（23）有如下形式的解

G（z）满足二阶线性常微分方程

其中，λ，μ为常数.将方程（24）代入方程（23），结合方程（25）可以得到方程（1）的3种形式的行波解：

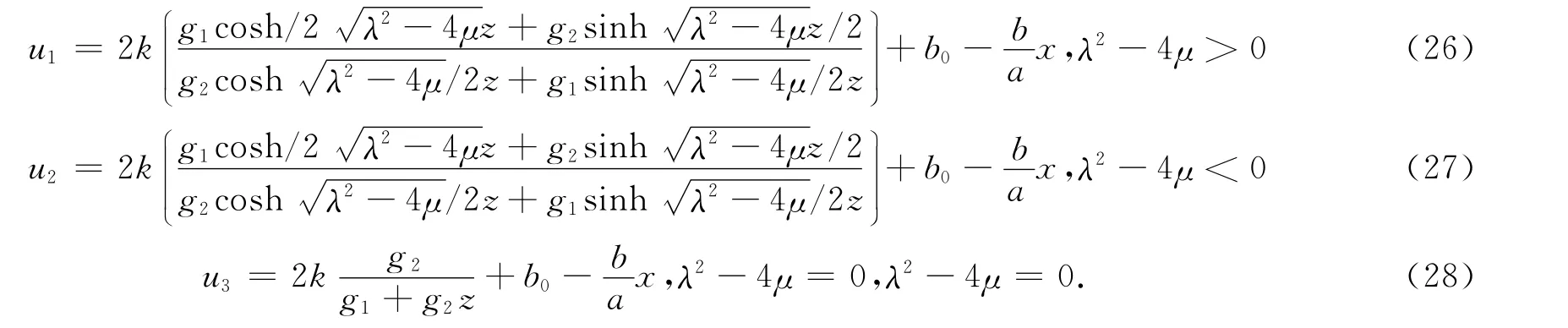
情况（Ⅲ）：令C1≠0，C2＝C3＝0＝C4＝0，P1（t）≠0，P2（t）≠0.通过求解特征方程就可以得到其不变解为

将方程（29）代入方程（1）可得

假设方程（30）有如下形式的解

通过求解可知方程（1）有如下形式的解

情况（Ⅳ）：令C1＝C2＝C4＝0，C3≠0，P1（t）＝P2（t）＝0.解特征方程就可得到其不变解为

将方程（33）代入方程（1）得到

假设方程（34）有如下形式的解

通过求解可知方程（1）有如下形式的解

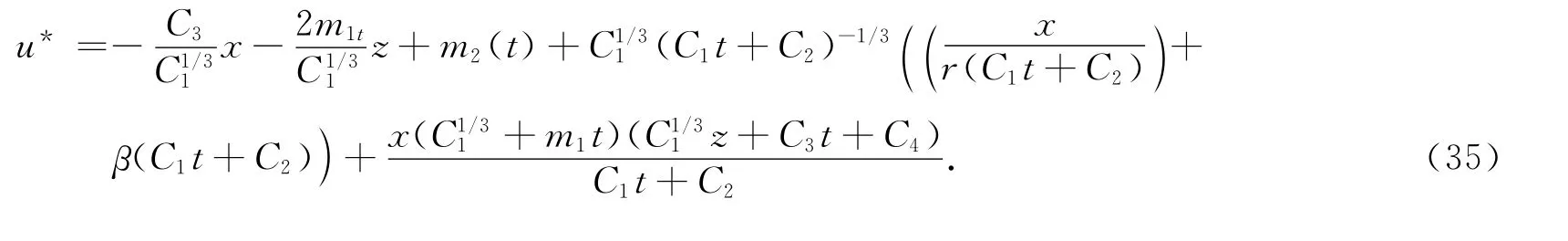
3 结 论

（1）通过改进的CK直接法推导出了定理1，并且通过定理1建立了（2＋1）维CBS方程新解和旧解之间的联系，并由此得到了该方程的对称.

（2）基于（2＋1）维CBS方程的一个已知解，通过选取任意函数的形式，并且利用得到的解之间的关系可得该方程具有结构丰富的解.这些解在数学及物理中有着重要的应用，这种方法也适用于其他高维的非线性微分方程的求解.

［1］OLVER P J.Application of lie group to differential equations［M］.Berlin：Springer，1986：13－90.

［2］楼森岳，唐晓燕.非线性数学物理方法［M］.北京：科学出版社，2006：314－322.LOU Senyue，TANG Xiaoyan.Nonlinear mathematical physics method［M］.Beijing：Science Press，2006：314－322.

［3］CLARKSON P A.KRUSKAL M D.New similarity reductions of the boussinesq equation［J］.J Math Phys，1989，30：2201－2212.

［4］LOU S Y，MA H C.Non－Lie symmetry groups of（2＋1）－dimensional nonlinear systems obtained from a simple direct method［J］.J Phy A：Math Gen，2005，38：129－137.

［5］MA H C，DENG A P，WANG Y.Exact solution of a KdV equation with variable coefficients［J］.Computers and Mathematics with Applications，2011，61：2278－2280.

［6］ZHANG L H，LIU X Q.New exact solutions and conservation laws to （3＋1）－dimensional potential－YTSF equation［J］.Commun Theor Phys，2006，45：487－492.

［7］BRUZON M S，GANDARIAS M L，MUIEL C，et al.The Calogero－Bogoyavlenskii－Schiff in （2＋1）－dimensions［J］.Theoretical and Mathematical Physics，2003，137（1）：1367－1377.

［8］WAZWAZ Abdul－Majid.Multiple－soliton solutions for the Calogero－Bogoyavlenskii－Schiff，Jimbo－Miwa and YTSF equation［J］.Appl Math Comput，2008，203（2）：592－597.

［9］智红燕.（2＋1）维Calogero－Bogoyavlenskii－Schiff方程的对称约化及其新的类孤子解 ［J］.中国石油大学学报：自然科学版，2010，34（3）：170－173.ZHI Hongyan.Symmetry reduction and some new soliton－like solutions of（2＋1）－dimensional Calogero－Bogoyavlen－skii－Schiff equation［J］.Journal of China University of Petroleum：Natural Science，2010，34（3）：170－173.

［10］张焕萍，陈勇，李彪.（2＋1）维广义 Calogero－Bogoyavlenskii－Schiff方程无穷多对称及其约化［J］.物理学报，2009，58（11）：7393－7396.ZHANG Huanping，CHEN Yong，LI Biao.Infinitely many symmetries and symmetry reduction of（2＋1）－dimensional generalized Calogero－Bogoyavlenskii－Schiff equation［J］.Journal of Physics，2009，58（11）：7393－7396.

［11］GANDARIAS M L，BRUZON M S.Symmetry group analysis and similarity solutions of the CBS equation in（2＋1）dimensions［J］.Appl Math Mech，2008（8）：10591－10592.

［12］WAZWAZ A M.New solutions of distinct physical structuresto high－dimensional nonlinear evolution equations［J］.Applied Mathematics and Computation，2008，196：363－370.