城市居民用户小时用气量预测的研究

深圳市燃气集团股份有限公司 何俊龙华润燃气控股有限公司 彭知军

0 概述

随着城市建设的快速发展，天然气管道已经延伸至城市的每一个角落。在燃气供应过程中不可避免地会发生地下燃气管道抢修、维修或管道接驳等作业。为了不影响用户的正常用气，通常采用的方法是利用临时供气来解决非正常工况下(燃气管道抢维修或接驳作业等)燃气用户的连续用气问题。临时用气量估算偏小，会导致供气压力不足或停气；用气量估算过大，由于LNG钢瓶不易储存，临时供气时间较长或等待时间因故增加会导致蒸发气体放散，从而增加了作业工作量。所以，在临时供气作业实施前应提高所需用气量估算值的准确性。可能影响居民用气量因素很多，受到用气设备、生活水平和生活习惯、户均人口数等多种因素影响，估算的难度很大。

本文通过采用指数平滑法与抽样分析相结合的方法对南方某居民小区小时用气量进行了估算，提出了估算方法和路径。该小区于2006年进行天然气转换，住户和用户数量稳定。调查从2012年5月开始，到2013年4月结束。从大量统计数据来看小时负荷呈现趋势性、较强的随机性和以24 h为周期的周期性变化规律；日负荷呈现较强的趋势性、随机性的变化规律；月负荷呈现趋势性、较强的以12 个月为周期的周期性变化规律。本文通过以下两个步骤来估算该小区小时用气量:(1)通过指数平滑法预测日用气量；(2)通过抽样分析统计得出小时不均匀系数规律。

1 指数平滑法预测日用气量

1.1 指数平滑法

指数平滑预测法是采取渐消记忆的方式，利用逐步衰减的不等权平均办法进行数据处理的一种预测方法，其基本思想是在预测过程中认为，越近期的数据越能反映当前的情况，对考虑今后的发展就越有直接的意义。该方法简单实用，能通过平滑作用，自动清除数据序列中的随机波动，尤其是那些不符合统计规律的偶然性波动，适用于燃气用气量中、短期预测。通常使用的指数平滑法分为一次指数平滑法和二次指数平滑法。

1.1.1 一次指数平滑法

一次指数平滑法的基本公式为:

式中:St——时间t的一次平滑值；

a——平滑常数，其取值范围为[0，1]；

Yt——时间t的实际值；

St-1——时间t-1的一次平滑值。

由该公式可知:

(1)St是Yt和St-1的加权算数平均数，随着a取值的大小变化，决定Yt和St-1对St的影响程度，当a取1时，St=Yt；当a取0时，St= St-1。

(2)St具有逐期追溯性质，可探源至St-t+1为止，包括全部数据。其过程中，平滑常数以指数形式递减，故称之为指数平滑法。

(3)尽管St包含有全期数据的影响，但实际计算时，仅需要两个数值，即Yt和St-1，再加上一个常数a，这就使指数滑动平均具逐期递推性质，从而给预测带来了极大的方便。

(4)当欲用指数平滑法时才开始收集数据，则不存在Y0，无从产生S0，自然无法据指数平滑公式求出S1，指数平滑法定义St为初始值。初始值的确定也是指数平滑过程的一个重要条件。

如果能够找到Y1以前的历史资料，那么，初始值St的确定是不成问题的。数据较少时可用全期平均、移动平均法；数据较多时，可用最小二乘法。但不能使用指数平滑法本身确定初始值，因为数据必会枯竭。

如果仅有从Y1开始的数据，那么确定初始值的方法有:

(1)取S1等于Y1；

(2)待积累若干数据后，取S1等于前面若干数据的简单算术平均数。

1.1.2 二次指数平滑法

二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地记性预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。

二次指数平滑法的公式为:

1.2 指数平滑预测模型

用指数平滑法进行预测，有线性模型和二次曲线模型。

1.2.1 线性模型

用于未来负荷预测的线性模型为:

式中:Xt+T——为t+T时刻的预测值；

T——为预测周期；

bt——为动态参数；

ct——为动态参数。

该模型要求Yt+T具有线性趋势，但不是在整个时段内拟合一条直线，而是在每个t时刻，动态地确定参数bt和ct，因此t时刻以前的预测值并不一定在一条直线上，但t+T时刻的预测是按Yt+T模型预测，由于模型的限制，预测时间步长不宜太大，一般作T=1一步预测。

根据平滑预测技术滞后的特点，还由于随机干扰的存在，参数bt和ct的合理估计为:

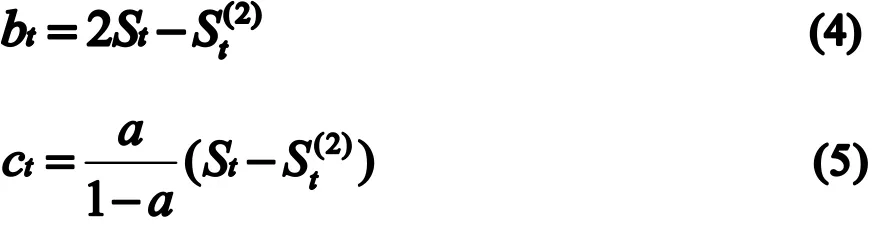
1.2.2 二次曲线模型

如果时间序列所体现的事物过去发展变动的趋势呈二次曲线型，则需要采用二次曲线模型进行预测，为:

式中:bt——为动态参数；

ct——为动态参数；

dt——为动态参数。

三个待定参数的估值公式分别为:

二次指数平滑值是对一次指数平滑值的计算。类似计算三次指数平滑值。

该小区调查时间365天内用气量曲线图见图1。

图1 该小区365天用气量曲线

将其中1～90天的用气量利用指数平滑法进行模拟计算，得出采用a取0.3时的线性模型精确度最高。原始数据和预测数据计算结果对比见图2。

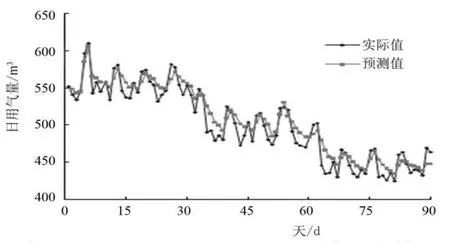
图2 a=0.3线性模型

1.3 利用灰色理论进行精度检验

针对上述预测值，可以利用灰色理论中预测精度的方法来检验，主要是检验小误差概率和后验差比值[5-6]。其计算步骤如下:

(1)求残差均值，公式为:

式中:ε——为残差均值；

ε(i)——为残差。

代入数据得出该小区残差均值为6.1 m3；

(2)求残差的方差，公式为:

式中:D——为残差方差。

代入数据得出该小区残差方差为17.4；

(3)求原始数值均值，公式为:

式中:E0——为原始数值均值；

E(i)——为原始数值，即每天用气量数值。

代入数据得出该小区原始数据均值为495 m3；

(4)求原始数值方差，公式为:

式中:D0——为原始数值方差。

代入数据得出该小区原始数值方差为52。

(5)求后验差比，公式为:

式中:C——为后验差比值。

代入数据得出该小区后验差比值为0.335；

(6)求小误差概率，公式为:

式中:P——为小误差概率

代入数据得出该小区小误差概率为100%。

表1 预测精度等级

小误差概率和后验差比值等级标准见表1，由上所得本次预测模型误差分析数据见表2。对比得出该模型预测精度为一级，预测的数值较准确，符合实际工程使用要求。

表2 a=0.3线性模型预测精度误差分析

2 抽样分析统计得出小时不均匀系数平均值

抽样分析为按照随机原则从调查对象中抽取一部分单位进行调查，并以调查结果对总体数量特征做出具有一定可靠程度的估计与推断，从而认识总体的一种统计方法，它的目的却在于取得反映总体情况的信息资料，因而，也可起到全面调查的作用。概率抽样是按照概率论和数理统计的原理从调查研究的总体中，根据随机原则来抽选样本，并从数量上对总体的某些特征作出估计推断，对推断出可能出现的误差可以从概率意义上加以控制。

随机选取调查周期中每月的15日的小时用气量数据，再选取出其中周一到周日各1天的数据，根据时不均匀系数的定义，计算出每日各个小时的不均匀系数见表3。

表3 每日小时不均匀系数

通过表3可知，小时不均匀系数随月份变化没有明显的规律，但跟是否为工作日有关，周六、周日变化相对来讲要比周一至周五平缓些，故将工作日和非工作日分开分析。可得出工作日各小时不均匀系数的平均值，即工作日小时不均匀系数变化规律见表4。

表4 工作日小时不均匀系数平均值

由于实际情况下，涉及到临时供气，最少需准备一瓶气(约充装70 m³)。对于该小区24小时中每个单独的小时用气量和用气低峰期的用气量均未超过一瓶气的充装量，临时供气所充装的气量必然能满足实际用气量，所以只需确保高峰期用气量的相对误差符合实际需要即可。由图可知工作日用气高峰期主要集中在10～13点、19～22点，根据相对误差公式:

式中:d～——为相对误差；

E(i)——为原始数值，即每天用气量数值；

E(i)——为预测数值，即每天用气量数值。

根据表4数据求出两段时间用气高峰期的相对误差见表5。

表5 用气高峰期相对误差

对于工程当中的相对误差允许范围无相关规定，一般认为误差在±10%内符合工程使用要求。从上表得出数据可知误差小于±10%，符合实际工程使用要求。

同理，可以求出周末用气量小时不均匀系数规律。由于周末参考数据过少，故将2012-12-15(周六)的数据加入进行估算，得出周末用气量小时不均匀系数平均值见表6。同上方法对预测数据进行检验，得出误差在±10%范围内，符合实际工程使用要求。

表6 周末小时不均匀系数平均值

3 某次作业临时供气量估算

2013年6月5日燃气抢修作业需对居民用户临时供气，临时供气用户数为2 016户，时间为中午13:00～14:00，用上述方法预测该小区在这一时间段内用气量为42.6 m³，实际为41.9 m³，误差为1.6%。

通过估算出日用气量，再用小时不均匀系数算出小时用气量的方法对估算小区小时用气量是非常准确的。误差的存在是难免的，如果估算量偏小，会导致用户无法正常用气，但是由于小区管网内会有一定的存气量，故在上述误差范围内所造成估气量小于实际用气量情况下，小区居民用户正常用气不受影响。

4 结语

本文通过建立用户用气量数据库，来预测指导生产。以上方法如能推广到任一小区进行小时用气量的预测，可以准确地预测出该小区未来某一小时用气量，能够保证非正常工况下(燃气管道抢维修或接驳作业等)燃气用户正常连续用气，并减少不必要的工作量。