基于PID调节器的Buck电路的系统设计与仿真
刘晓东,韦燚(.上海海事大学物流工程学院电力电子与电力传动系,上海 0306;.上海海事大学物流工程学院电工理论与新技术系,上海 0306)
基于PID调节器的Buck电路的系统设计与仿真
刘晓东1,韦燚2
(1.上海海事大学物流工程学院电力电子与电力传动系,上海 201306;2.上海海事大学物流工程学院电工理论与新技术系,上海 201306)
PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛应用于工业过程控制。尤其是适用于可建立精确数学模型的确定性控制系统[1]。一般的DC/DC 变换器是一种非线性系统,单一的控制策略往往不能满足系统动态和静态指标的要求,因此需要加上一个负反馈构成一个闭环系统来提高输出精度和动态特性。针对这种情况,本文设计了一个PID调节器,并与Buck电路构成一个负反馈系统。通过小信号建模,得出Buck变换器的数学模型,并通过Matlab软件中sisotool工具模块仿真并设计出PID调节器的参数,极大地改善了 DC-DC 变换器系统的动态特性。
电力电子与电力传动;PID调节器;Sisotool;Buck变换器
0 引言
直流-直流变换电路(DC/DC Choppter)是将直流电源的恒定直流电压,通过电力电子器件的开关作用,变换为可调直流电压的电路[2]。直流斩波电路有很多种拓扑结构,根据电路形式的不同,非隔离型电路可以分为降压斩波电路、升压斩波电路、升降压斩波电路、Cuk斩波电路、Sepic斩波电路和Zeta斩波电路等。其中降压斩波电路也称Buck电路(如图1所示)。
本文以Buck电路为基础设计了一个PID调节器。假设电路中各元器件的参数值,通过小信号建模建立Buck电路的数学模型,分析计算所需负反馈系统的传递函数,通过传递函数的波特图分析设计PID调节器,利用Matlab软件中的Sisotool工具模块得到PID调节器的参数值,然后得到Buck电路与PID调节器共同构成的负反馈系统,并利用PSIM仿真软件得到系统的仿真电路,得到原始电路的输出电流和输出电压的图形,通过改变输入电压、输入电流等,得到新的输出电流和输出电压的图形,分析验证所设计的PID调节器的有效性。

图1 Buck电路Fig.1 The Buck circuit
2 Buck电路分析与PID调节器设计
2.1Buck电路参数选择
本文以Buck电路为基础设计PID调节器。假设电路模型中各元器件的参数值,其输入电压Vg=28V、电感L=50uH、电容C=500uH、电阻R=3Ω、输出电压V=15V、输出电流iioad=5A、静态占空比D=15/28=0.536、参考电压Vref=5V、静态控制电压Vc=DVM=2.14V。其中:Sensor gain为传感器增益;Compensator为补偿器;Pulse-width modulator为脉宽调制器;Error signal为误差信号;Transistor gate driver为晶体管栅极驱动器[3]。
2.2负反馈系统的传递函数及小信号建模
DC/DC变换器构成的负反馈控制系统如图2所示,其中G(s)为Gc(s)Gm(s)Gvd(s)。对于Buck变换器,其回路增益函数G(s)H(s)=Gc(s)Gm(s)Gvd(s)=Gc(s)Go(s)[4]。其中Go(s)=Gm(s)Gvd(s)H(s)为未加补偿网络Gc(s)时回路增益函数,是控制信号Vc(s)至反馈信号B(s)之间的传递函数;Gd(s)为DC/DC变换器占空比(s)与输出(s)之间的传递函数;Gm(s)为PWM脉宽调制器的传递函数(其中锯齿波幅度VM=4V);H(s)表示反馈分压网络的传递函数[4-5]。

图2 负反馈控制系统Fig.2 The system of degenerative feedback
利用小信号模型法求出Gvd(s)

原始回路增益函数Go(s)

通过Matlab中sisotool工具模块分析原始回路增益函数Go(s)的传递函数,输入其传递函数,得到传递函数的波特图如图3所示。
原始回路增益函数Go(s)是一个二阶系统,有两个极点,幅频图在低频段为水平线[6],幅值为dB,幅频的转折频率。相位裕量PM≈4.73°可见原始回路增益函数的频率特性的相位裕量太小,虽然系统是稳定的,但是存在较大的输出超越量和较长的调节时间。通常相位裕量在45°左右,因此需要加入补偿网络Gc(s),提高相位裕量和裕量增益。
2.3PID补偿器的设计
在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID算法是应用广泛的一种控制算法[7],PID算法的一般计算式及模拟控制规律表达式如(3)。

图3 原始回路增益函数的波特图Fig.3 The Bode of the original loop gain function

上式中u(t)为控制器的输出;e(t)为偏差,即设定值与反馈值之差;Kc为控制器的放大系数,即比例增益;Ti为控制器的积分常数;Td为控制器的微分时间常数。PID算法的原理即调节Kc、Ti、Td三个参数使系统达到稳定[8]。图1中DC/DC变化器中开关频率fs=100kHz,为了提高穿越频率,设加入补偿网络Gc(s)后,回路函数C(s)H(s)=Cc(s)Co(s)的增益交越频率fc(s)等于1/20的开关频率,于是交越频率

相位裕度为θ=50°。
因此补偿器的零点fz和极点fP为[9]
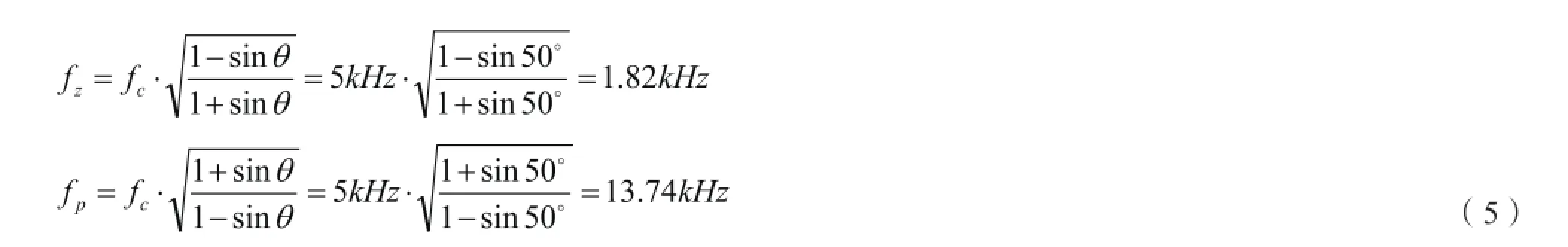
在Sisotool工具中对原始回路增益函数Go(s)添加补偿器的零点fz和极点fp如图4所示。
并且为了克服稳态误差大的缺点,可以加入倒置零点fl,从而构成PID调节器;根据电路图如图5所示,PID补偿网络的传递函数为:

根据图7所示Sisotool的参数设置,得到加入倒置零点后构成PID调节器的传递函数为:

根据上式计算可得PID调节器系统参数,假设C1=1μF、可以计算出C2=0.273μF、R2=290Ω、R2=3186Ω、R3=12Ω。
3 基于PSIM的电路图仿真与分析
本文通过PISM仿真软件对设计出的BUCK变换器与PID调节器所构成的反馈系统进行仿真验证,得到加入PID调节器前后Buck变换器的输出电流和电压图,以及当输入电压和输入电流发生突变时,验证所设计的PID调节器的调节能力。如下图所示,图8为通过PSIM仿真软件得到的原始Buck电路仿真图,图9为原始Buck电路的输出电压和输出电流。
加入PID调节器后的PSIM仿真电路图和输出电压电流图分别如图10和图11所示
实验验证当电压发生突变时,即在第0.006秒时加入扰动电压,原始电压由28V突变为30V时的电压电流变化情况,输出电压电流图分别如图12和图13所示。

图4 原始回路增益函数加入补偿零点和极点Fig.4 The original loop gain function is added to compensate the zeros and poles

图5 PID调节器原理图Fig.5 The schematic diagram of PID regulator

图6 加入倒置零点后的波特图Fig.6 Add an inverted zero

图7 Sisotool参数设置Fig.7 Set the parameter of Sisotool

图8 原始电路Fig.8 Original circuit

图9 Buck变换器系统的输出电压(下)和输出电流(上)Fig.9 The output voltage(lower)and output current(upper)of Buck converter

图10 Buck电路和PID调节器构成的反馈系统Fig.10 The feedback system composed of Buck circuit and PID regulator

图11 经PID调节后的输出电压(下)和输出电流(上)Fig.11 The output voltage (lower) and output current (upper)after PID

图12 电压突变时输出电流的变化Fig.12 Change of output current when voltage change

图13 电压突变时输出电压的变化Fig.13 Change of output voltage when the voltage change
实验验证当输入电流发生突变时输出电压电流的变化情况,在第0.009秒时加入电流扰动,在PSIM仿真的时,在0.009秒并联一个30欧姆的电阻,使电路输出电流发生突变。其PSIM仿真和输出电压电流图分别如图14和图15所示。

图14 电流突变时输出电流的变化Fig.14 Variation of output current in current mutation
4 结果分析与总结
本文给出了基于PID调节器和Buck电路所构成的反馈系统,该系统在突加2V负载电压扰动时,输出电压有0.02V的波动恢复时间约为0.002s;当负载电流有10%的突变扰动时,系统的电压有0.007V的波动,恢复时间为0.0003s。因此本次设计的PID补偿器符合设计要求,可以提高BUCK电路的输出精度和动态特性。
Buck变换器是DC/DC变换器中最具代表的性的拓扑结构之一。在实际工程中,Buck变换器的PID控制系统的PID参数的调节较为麻烦,往往需要大量的实验,择优才能找到合适的参数值[10]。本文建立的Buck变换器和PID控制算法的数学模型,在Matlab环境下通过仿真不断调节PID的各种参数,并通过对PID系统的仿真能够初步得到系统的参数值,对实际的调试有一定的参考意义。

图15 电流突变时输出电压的变化Fig.15 Variation of output voltage in current mutation
[1] 陶永华.新型PID控制及其应用[M].北京:机械工业出版社,2002. TAO Y H. New PID control and application[M]. Beijing:China Machine Press,2002.
[2] 王楠,沈倪勇,莫正康.电力电子应用技术[M].北京:机械工业出版社,2013. WANG N,SHEN N Y,MO Z K. Power electronics application technology[M]. Beijing:China Machine Press ,2013.
[3] Erickson R W,Maksimovi D .Fundamental of Power Electronics[M]. Germany:Springer,2001.
[4] 徐德鸿. 电力电子系统建模及控制[M].北京:机械工业出版社,2006. XU D H. Modeling and control of power electronic system[M]. Beijing:China Machine Press,2006.
[5] 桑绘绘,杨奕,沈彩琳.基于PID控制的Buck变换器仿真系统设计[J].南通大学学报,2011,10(1):24-28. SANG H H,YANG Y,SHEN C L. Design of simulation system for Buck converter based on PID control[M].Journal of Nantong University,2011,10(1):24-28.
[6] 胡寿松.自动控制原理[M].北京:科学出版社,2007. HU S S. Automatic control principle[M]. Beijing:Science Press,2007.
[7] 肖志坚,韩震宇,李绍卓.关于便携式电子设备新型无线充电系统的研究[J].自动化技术与应用,2007,26(12):46-48. XIAO Z J,HAN Z Y,LI S Z. A novel wireless charging system for portable electornic equipment[J]. Techniques of Automation&Application,2007,26(12):46-48.
[8] 倪晗悦,丁嘉毅,曹婷,等. 基于PID 及PWM 的无线传能系统研究[J].新型工业化,2014,4(9):56-61. NI H Y,DING J Y,CAO T,et al. Wireless energy transfer system based on PID and PWM[J].The Journal of New Industrizlization,2014,4(9):56-61.
[9] 张兰芸,姜孝华,何振辉,等.DC/DC 变换器研究与设计[J].电力电子技术,2007,41(8):45-47. ZHANG L Y,JIANG X H,HE Z H,et al.. Research and design of DC/DC converter[J]. Power Electronics,2007,41(8):45-47.
[10] 罗均,周玉美,胡钜奇,等.基于模糊的仿生机槭云台系统研究[J].新型工业化,2013,3(10):16-22. LUO J,ZHOU Y M,HU J Q,et al.Bionic PTZ system research based on fuzzy PID controlling[J].The Journal of New Industrizlization,2013,3(10):16-22.
System Design and Simulation of Buck Circuit Based on PID Regulator
LIU Xiao-dong1, WEI Yi2
(1. Department of Power Electronics and Electric Power Transmission, School of Logistics Engineering, Shanghai Maritime Univeristy, Shanghai 201306, China; 2. Department of Electrical Engineering Theory and New Technology, School of Logistics Engineering, Shanghai Maritime Univeristy, Shanghai 201306, China)
PID control is one of the earliest developed control strategy, because of its simple algorithm, good robustness and high reliability, is widely used in industrial process control. Especially, it is suitable for the deterministic control system which can establish the precise mathematical model. DC / DC converter is a nonlinear system, a single control strategy often fails to meet the requirements of the system dynamic and static performance. Therefore, , adding a negative feedback to constitute a closed-loop system to improve the output precision and dynamic characteristic is necessary. In view of this situation, this paper designs a PID regulator, and constitute a negative feedback system with Buck circuit. Getting the mathematical model of the buck converter by the small signal modeling, and Designing the parameters of the PID regulator through MATLAB software SISOTOOL tool module, greatly improve the dynamic characteristics of the DC-DC converter system.
Power electronics and power transmission; PID regulator; Sisotool; Buck converter
10.3969/j.issn.2095-6649.2015.11.005
LIU Xiao-dong, WEI Yi. System Design and Simulation of Buck Circuit Based on PID Regulator[J]. The Journal of New Industrialization,2015,5(11): 27-33.
刘晓东(1990-),男,上海海事大学物流工程学院电力电子与电力传动系,硕士研究生,研究方向为电力电子技术及装置;韦燚(1991-),女,上海海事大学物流工程学院电工理论与新技术系,硕士研究生,研究方向为电工理论与新技术
本文引用格式:刘晓东,韦燚.基于PID调节器的Buck电路的系统设计与仿真[J]. 新型工业化,2015,5(11):27-33.

