SINS初始对准中光纤陀螺EMD滤波
王延东,杨春雷,董文辉
(中国科学院长春光学精密机械与物理研究所,吉林长春130033)
SINS初始对准中光纤陀螺EMD滤波
王延东*,杨春雷,董文辉
(中国科学院长春光学精密机械与物理研究所,吉林长春130033)
为了实现低成本SINS初始对准,降低对准过程复杂程度,提高系统对准精度,缩短对准时间,本文引入了EMD滤波技术。首先,采集IMU输出信号,根据EMD算法将信号分解为IMF簇,按照CMSE标准对信号进行重构,完成信号滤波处理;接着,按照AR模型对经EMD滤波前后的数据噪声进行建模;然后,分别利用原始信号和EMD降噪后信号进行SINS姿态粗对准;最后,根据IMU模型和SINS误差模型,采用零速对准方式,完成SINS精对准。实验结果表明:经EMD降噪后的信号粗对准精度为1.3°,精对准精度为0.87 mrad,精对准收敛时间为200 s。
经验模态分解;光纤陀螺;非线性滤波;初始对准;捷联惯导
1 引 言
捷联惯导系统(SINS)初始对准是导航领域的研究重点之一,惯性测量单元(IMU)尤其是陀螺的噪声水平直接影响初始对准精度。而在初始对准中,航向对准是重中之重。通常情况下,若航向对准精度达到1 mrad,需要0.01°/h的陀螺噪声水平,这种陀螺为导航级器件,造价相当昂贵。对于低成本SINS,初始对准依赖双天线GNSS、电子罗盘和光电经纬仪等外部参考信息,它们造价高、系统复杂,精度难以保证。因此对低成本惯性测量单元(IMU)降噪,使SINS完成自对准一直是导航领域重点研究方向之一。
近年来,运用现代信号处理技术降低陀螺噪声水平已经取得了较大进展,文献[1-2]表明,使用Morlet小波滤波技术能够明显降低陀螺噪声水平。但从根本上,小波降噪是将信号本身作为线性平稳信号处理,实质上为带通滤波器,而且对小波基、分解尺度和阈值估计依赖较大,若处理不当,信号极易失真。经验模态分解(EMD)是近年来信号处理领域的研究热门,由Huang.G.E提出[4],旨在针对非线性和非平稳性信号进行分析。EMD自适应地将信号按照振幅和频率将信号分解成一系列组分,单个组分称为一个本征模态函数(IMF),通过IMF簇不仅能够分析出信号的瞬时频率特性,还能按照设计带宽,重构出有效信号,降低信噪比,达到非线性、非平稳随机信号滤波的目的。EMD处理过程在时域内完成,计算量相对于小波降噪大幅减小[5-8]。本文将EMD降噪应用于光纤陀螺降噪和SINS初始对准中,按照递推最小均方根(CMSE)标准确定IMF个数,对信号重构,按照零速修正(ZUPT)方式完成SINS初始对准。
2 SINS初始对准
SINS初始对准的数学意义是确定SIN方程的积分初值。若积分初值误差较大,则在SINS误差传播过程中不断累积,直接影响导航系统精度。SINS初始对准包括位置对准、速度对准和姿态对准,位置对准和速度对准完全依赖于外部参考,而位置和速度的装订实现简单,GNSS等定位技术完全可以实现。而姿态对准难度较大,所以初始对准一般都是姿态对准。初始对准分为粗对准和精对准两个步骤。
2.1 SINS粗对准
SINS粗对准依赖地球在惯性空间的基本物理属性实现,体现在地球重力和地球转速两个物理常量。通过捷联安装在载体上的IMU中加速度计敏感的重力分量确定的俯仰角和滚转角,即水平对准过程。通过陀螺敏感的地球转速的分量确定航向角,即罗经对准过程。
本文选择当地地理坐标系(t系)为导航坐标系(n系),θ和φ分别表示俯仰角和滚转角、和表示体系下加速度计测量的比力值。水平对准过程公式为:

罗经对准根据载体系与导航系角速度的关系确定。陀螺测量的角速度为;地球转速在地球系表示为;导航系转换至载体系(b系)的方向余弦矩阵为;地球系(e系)转换至导航系的方向余弦矩阵为二者关系为:
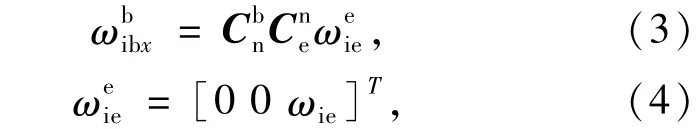
式中,ωie=7.292 115×10-5rad/s表示地球转速标量。根据二者关系可以计算出航向角ψ的余弦表达式和正弦表达式:
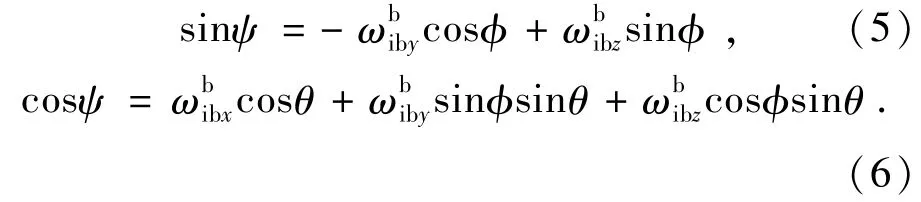
因此航向角为:

在水平对准中,地球加速度的测量值显著,通常1 mg误差水平的加速度计即可满足1 mrad俯仰角和滚转角对准精度,低成本的加速度计即可实现;而罗经对准受陀螺误差影响显著。L为地理纬度,δfy为东向加速度计误差,δωy东向陀螺误差,则航向角对准误差为:

因此,由测量原理可知,若得到可信航向对准精度,陀螺误差至少小于地球转速3个量级,且随着纬度的升高,对陀螺要求就越严格。
2.2 SINS精对准
SINS在粗对准的基础上,利用经典控制理论或最优估计理论,使姿态角不断收敛于真值的过程。对于静基座系统,一般采用零速修正法(ZUPT)。所谓ZUPT指的是,在静止条件下,载体的速度为零,由于IMU的误差,SINS速度存在误差,以此作为量测值,不断更新修正惯性器件、位置、速度和姿态的方法。
IMU中加速度计和陀螺存在不同的误差特性。加速度计误差相对于陀螺误差对初始对准影响较小。在SINS初始对准中,主要影响解算精度陀螺随机误差指标为白噪声、零偏不稳定性和角度随机游走。白噪声为噪声的高频组分,通过滤波技术可以达到降噪的目的。相关噪声表现为低频慢变漂移,可通过马尔科夫过程或AR模型进行建模[7]。陀螺的零偏不稳定性误差源于内部电路和结构设计,由于零偏不稳定性的低频特性,在陀螺测量值中变现为多次上电零偏重复性。随机游走在陀螺噪声中表现为低频形式,误差源于光电探测器的热噪声和杂散噪声。慢变漂移、零偏不稳定性和随机游走组合形成随机信号的低频段,从白噪声中将三种误差源分离,分别进行处理,能够提高SINS初始对准的精度。
静基座ZUPT对准在粗对准计算的初值基础上采用Kalman滤波的方式对导航状态误差量进行最优估计。Kalman滤波器的状态变量为位置误差、速度误差、失准角以及IMU误差。δr为位置误差,δv为速度误差,φ为姿态失准角,aB加速度计零偏,gB为陀螺零偏。以下角标n、e和d表示导航系的北向、东向和地向,则SINS零速更新Kalman滤波器状态变量为:

根据SINS误差传播方程,Ω为地球转速,R为地球平均半径,τa和τg表示加速度计和陀螺的慢变漂移时间常数。则Kalman滤波器状态矩阵为:

精对准Kalman滤波器的量测值为水平速度误差和地球转速测量误差。所以系统的量测方程为:

Kalman滤波器按照量测周期不断更新,导航计算机以此对SINS闭环修正,直到估计协方差收敛至设计指标。
3 EMD滤波器设计方法
3.1 EMD筛选过程
EMD是针对非线性和非平稳信号的时域分析算法,这种方法具有正交性和完备性。EMD的基本思想是:对于给定信号x(t),通过筛选过程将其分解为IMF簇。IMF具有与x(t)相同的时间尺度,筛选自适应地将给定信号分解与x(t)相同的IMF。EMD可假设为一种小波分解的方式,这种小波分解可以自适应地将信号分解为一系列信号成分,任意一个IMF为x(t)的一个频带[10-12]。IMF必须满足以下两个条件:
(1)零点数目与极值点数目相同,或者至多相差一个;
(2)函数由局部极大值点构成的包络线和由局部极小值构成的包络线的均值为零。
第一个限制条件保证了波形的局部对称;第二个条件将传统的全局条件修改为局部条件,是一种对信号可操作性的必要近似。EMD筛选过程见图1。
图1的筛选方法经i次循环获得的h满足IMF定义的两个条件。经过筛选过程x(t)能够重构为IMF簇和残差rc(t)之和:
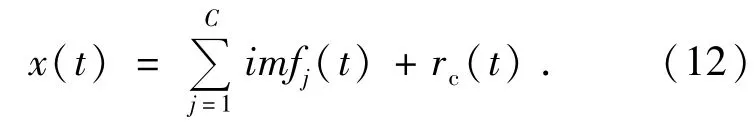
根据IMF筛选过程可以看出,对于特定信号x(t),EMD先通过极值点拟合其包络线,再由上、下包络线求信号的均值曲线,确定信号的IMF。包络线构造影响着EMD的全过程,决定EMD分解结果和分解精度。EMD方法中常用的拟合信号包络线方法有三次样条插值法、多项式插值法、分段Hermit插值等。其中三次样条插值是现有文献中普遍推荐的方法。样条插值既能克服高次多项式插值的缺陷,又能保证曲线的光滑[13-14]。先被提取的IMF频带比后提取的IMF的高。EMD不使用预定滤波器和小波方程,所以经验模态分解是完全的数据驱动方法。

图1 EMD流程图Fig.1 Flow chart of EMD
3.2 EMD筛选过程停止准则
EMD是一个筛选过程,过多地重复筛选会导致基本模式IMF变成纯粹的频率调制信号。为了保证IMF保存足够的反映物理实际的幅度和频率调制,必须确定分量终止条件,用于判定筛选每一阶IMF时的终止条件。Huang.G.E提出了一种类似于Cauchy收敛准则的标准,此准则通过限制两个连续处理结果之间标准差的大小确定[15]:

其中,SD的取值在0.2~0.3之间。
3.3 EMD滤波器
IMF筛选过程中,先筛选出IMF为x(t)的高频组分信号,后筛选出的IMF为信号的低频组分。所以,考虑信号系统x(t)被白噪声干扰,后筛选的IMF信噪比大于先筛选的IMF信噪比。根据这个思路,对于IMF簇{imfi},给定索引js,则{imfj>js}包含了信号更重要的能量分布,信噪比高,反映了信号的有效成分。而{imfj<js}为信号的高频噪声成分,在x(t)的重构中,{imfj<js}不被采用,所以以{im fj<js}为基础重构。EMD滤波的主要问题是,因为信号的噪声水平不可知,IMF解析表达式无法直接获得,EMD滤波结果依靠数值计算方式。
假设确定信号y(t)被加性高斯白噪声z(t)破坏:

对于观测信号x(t),滤波的主要目的是得出从确定信号y(t)的近似值,保证其均方差最小MSE:
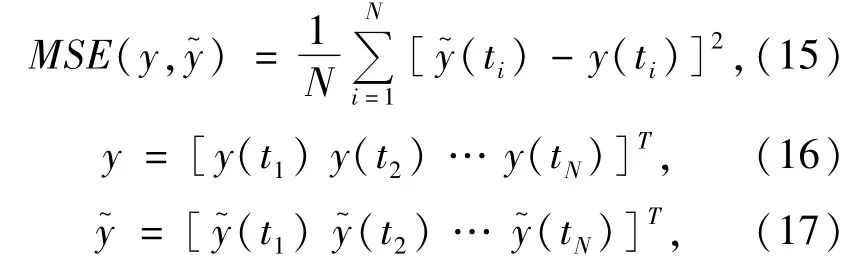
式中,N表示信号的长度。因为y(t)无法获得,采用最小连续均方差(CMSE)作为滤波结果判据:
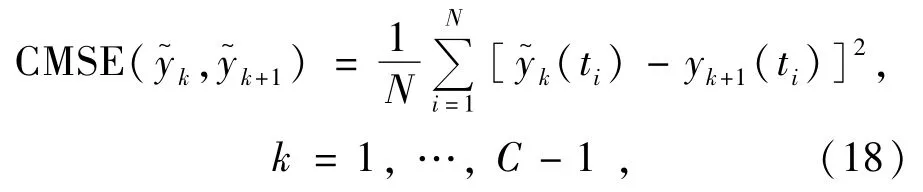
化简为:

CMSE判据将x(t)的信噪比增加到第k个imf的水平[16-17]。所以索引jS的数学表达式:

EMD滤波的步骤见图2。

图2 EMD滤波流程图Fig.2 Flow chart of EMD filter
4 实验对比及数据分析
根据EMD和SINS ZUPT初始对准算法设计系统实验。被测对象为某SINS/GPS组合导航系统,IMU中采用光纤陀螺和石英加速度计,GPS接收机为单点接收机,用于位置和速度的初始化。实验设备包括三轴仿真转台和GPS模拟器,三轴仿真转台通过使用光学设备校准初始航向,见图3。将组合导航系统安装于三轴转台上,设置转台初始姿态:滚转角为0°,俯仰角为30°,航向角为-10°。对使用EMD滤波前后的IMU数据进行分析对比,验证其初始对准的效果。

图3 SINS初始对准系统测试Fig.3 SINS initial alignment test
4.1 惯性器件EMD滤波分析
按照图1和图2的流程对陀螺和加速计EMD滤波,滤波前后统计量见表1。加速度计滤波结果见图4,陀螺滤波结果见图5。在图4和图5中,左侧为惯性器件输出值,右侧为EMD滤波后降噪结果,经EMD滤波后,信号的高频噪声全部滤除,保留的低频结果反应了噪声的慢变漂移。从表1得出结论:通过EMD滤波后,信号统计特征量均值不变;而标准差减小了两个量级,滤波效果明显。

表1 IMU EMD滤波前后统计量对比Tab.1 Statistical comparison before and after IMU EMD filtering

图4 光纤陀螺EMD滤波前后对比Fig.4 Comparison of fiber gyro before and after EMD filter
4.2 粗对准结果对比
按照式(1)~(7)对SINS分别使用IMU滤波前后的数据进行粗对准,结果见图6,(a)~(c)为原始结果,(d)~(f)为滤波后结果。从图6中能够看出,IMU原始信号完全无法进行航向对准,而滤波后的数据能够将对准结果的标准差控制在±1.5°之内,说明了经过滤波降噪后的低等级惯性器件在短时间内具备SINS自主粗对准的水平。
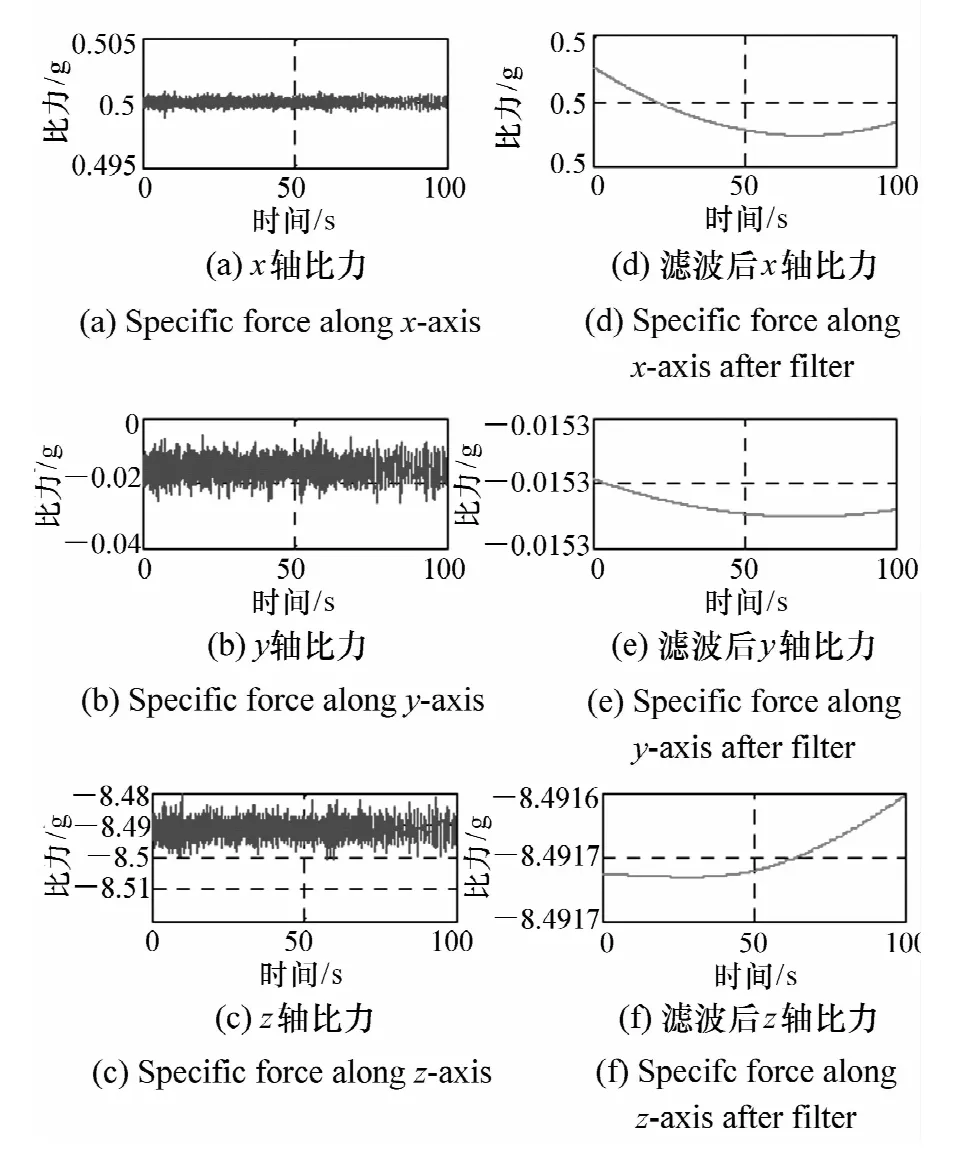
图5 加速度计EMD滤波前后对比Fig.5 Comparison of accelerometer before and after EMD filter

图6 IMU EMD滤波前后粗对准结果对比Fig.6 Comparison of coarse alignment before and after EMD filter
4.3 精对准结果对比
精对准以ZUPT方法进行,以航向角为例,分析精对准结果。因为原始数据的粗对准结果无法计算准确可靠的航向角,所以对于原始数据的精对准初始航向角采用了EMD滤波数据的粗对准结果,使二者具有可比性。航向角对准结果见图7,利用原始数据进行航向角对准,剔除趋势项计算标准差,其噪声水平在1°左右;而经EMD滤波后的航向角精对准过程,对收敛后数据计算标准差,方差水平为0.87 mrad,满足了一般导航系统的初始对准要求。协方差矩阵对角线平方根为Kalman滤波器效果的重要指标,一般用来评价滤波器的收敛时间。图8为航向角EMD滤波前后协方差估计平方根值,结果表明,EMD滤波前协方差在10 min内无法收敛;而EMD滤波后的协方差在200 s内即完成收敛,其滤波结果为最优估计结果。

图7 EMD滤波前后航向角初始精对准结果Fig.7 Initial fine alignment of azimuth angle before and after EMD filter
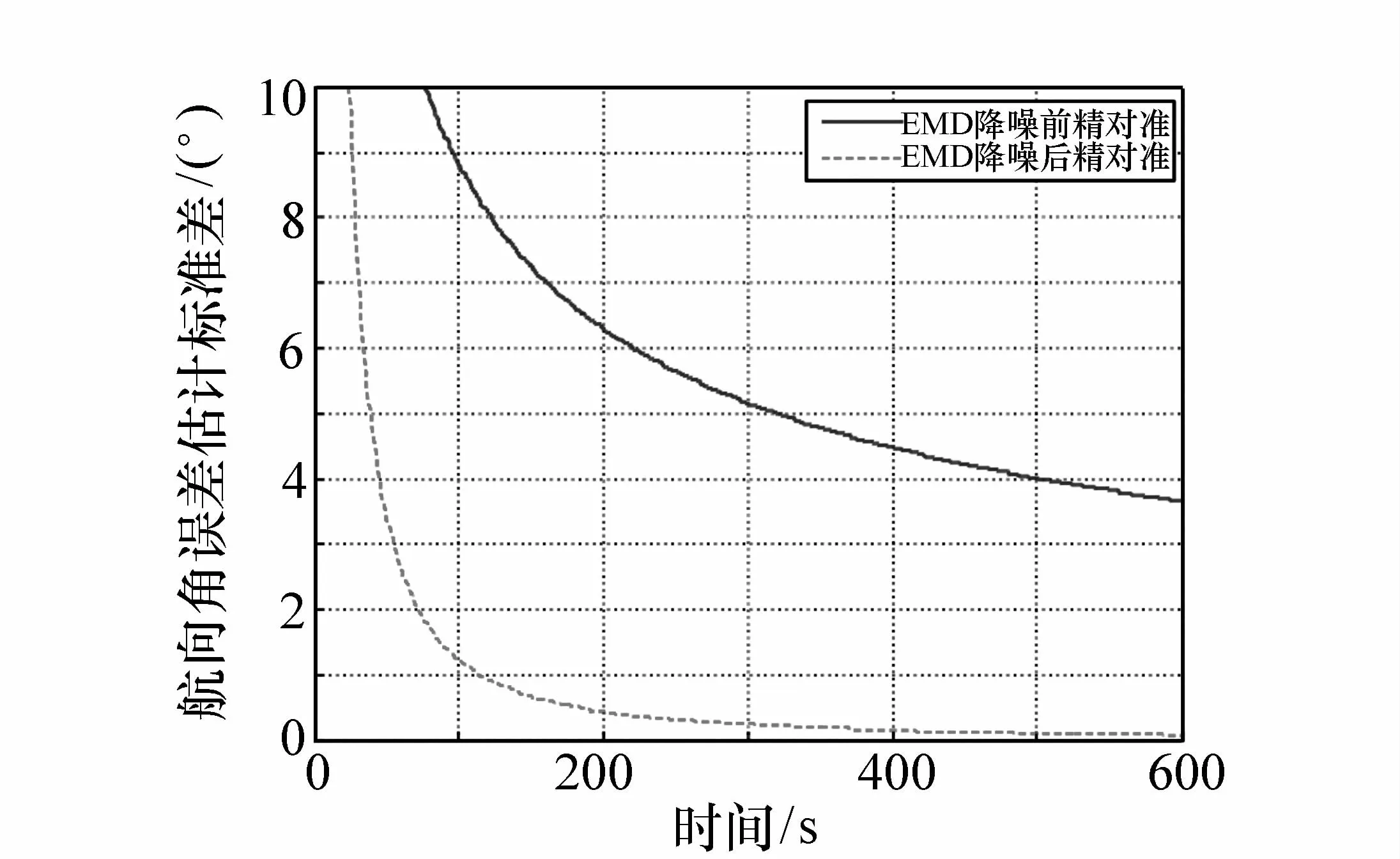
图8 EMD滤波前后航向角初始精对准估计协方差Fig.8 Initial fine alignment estimation covariance of azimuth before and after EMD filter
5 结 论
本文针对低成本SINS初始对准,引入EMD滤波技术,解决了SINS自主粗对准和精对准,姿态对准过程无需外部信息参考。首先系统介绍了SINS初始对准原理和过程,说明低成本SINS航向角不能自主对准的原因;然后研究了EMD筛选过程,提出了EMD滤波方法;最后通过实验对比EMD滤波前后IMU噪声水平、初始对准精度和Kalman滤波器收敛时间。实验结果证明:本文提出的EMD滤波方法能够提高光纤信噪比35 dB。EMD降噪后数据精对准过程在200 s内即可完成,航向角精对准精度为1 mrad。
[1] 郭丽君,宁亮,孔梅,等.谐振式集成光学陀螺解调特性分析[J].中国光学,2014,7(4):651-656.
GUO L J,NING L,KONGM,etal..Demodulation characteristics of resonator integrated optical gyro[J].Chinese Optics, 2014,7(4):651-656.(in Chinese)
[2] 徐丽娜,邓正隆.陀螺仪漂移特性的小波分析[J].中国惯性技术学报,2001,9(3):57-60.
XU L N,DENG ZH L.Wavelet analysis on gyro drift rate[J].J.Chinese Inertiao Technology,2001,9(3):57-60.(in Chinese)
[3] HUANG N E,WU M L,QUW D,etal..Applications of Hilbert-Huang transform to non-stationary financial time series analysis[J].Applied Stochastic Models in Business and Industry,2003,19:245-268.
[4] 王永红,梁恒,王硕,等.数字散斑相关方法及应用进展[J].中国光学,2013,6(4):470-480.
WANG Y H,LIANG H,WANG SH,et al..Advance in digital speckle correlationmethod and its applications[J].Chinese Optics,2013,6(4):470-480.(in Chinese)
[5] 刘伟宁.基于小波域扩散滤波的弱小目标检测[J].中国光学,2011,4(5):503-508.
LIUW N.Dim target detection based on wavelet field diffusion filter[J].Chinese Optics,2011,4(5):503-508.(in Chinese)
[6] 刘希佳,陈宇,王文生,等.小目标识别的小波阈值去噪方法[J].中国光学,2012,5(3):248-256.
LIU X J,CHEN Y,WANGW SH,et al..De-nosing algorithm of wavlet threshold for small target detection[J].Chinese Optics,2012,5(3):248-256.(in Chinese)
[7] 米剑,张春熹,李铮,等.偏光干涉对光纤陀螺性能的影响[J].中国光学,2005,26(8):1140-1144.
MI J,ZHANG CH X,LIZH,etal..Effectof polarization interference on fiber optic gyro performance[J].Chinese Optics,2005,26(8):1140-1144.(in Chinese)
[8] 李新忠,岱钦,王希军,等.多尺度小波降噪的数字散斑相关搜索[J].光学精密工程,2007,15(1):58-63.
LIX ZH,DAIQ,WANG X J,et al..Digital speckle correlation method ofmulti-scale wavelet noise reduction[J].Opt.Precision Eng.,2007,15(1):58-63(in Chinese)
[9] 薛海建,郭晓松,周召发,等.基于经验模分解的陀螺信号去噪[J].机械科学与技术,2013,32(7):1049-1053.
XUE H J,GUOX S,ZHOU ZH F,etal..A de-noisingmethod for gyro signal based on empiricalmode decomposition[J].Mechanical Science and Technology for Aerospace Engineering,2013,32(7):1049-1053.(in Chinese)
[10] 喻敏,王斌,王文波,等.联合EMD与核主成分分析的激光陀螺信号消噪[J].武汉大学学报·信息科学版,2015,40(2):233-237.
YU M,WANG B,WANGW B,etal..Laser gyro signal de-noising based on EMD and kernel principal componentanalysis[J].Geomatics and Information Science ofWuhan University,2015,40(2):233-237.(in Chinese)
[11] 李家齐,王红卫,刘爱东.基于改进型经验模分解的陀螺漂移趋势提取[J].系统工程与电子技术,2005,27(6):1080-1082.
LIJQ,WANG HW,LIU A D.Trend extraction of gyro′s drift based on modified empiricalmode decomposition[J].Systems Engineering and Electronics,2005,27(6):1080-1082.(in Chinese)
[12] PENG Z K,TSEA PW,CHU F L.A comparison study of improved Hilbert Huang transform and wavelet transform:Application to fault diagnosis for rolling bearing[J].Mechanical Systems and Signal Processing,2005,19:974-988.
[13] ERIC D,JACQUES L,OUMAR N.Empiricalmode decomposition:an analytical approach for sifting process[C].IEEE Signal Processing Letters,2005,12(2):112-114.
[14] PATRICK F,GABRIEL R,PAULO G.Empiricalmode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.
[15] 刘鲁源,陈玉柱,陈刚,等.基于小波变换的陀螺漂移建模与实验研究[J].中国惯性技术学报,2004,12(1):61-65.
LIU LY,CHEN Y ZH,CHENG,etal..Modeland experiment research ofgyro drift rate based on wavelet transform[J].J.Chinese Inertiao Technology,2004,12(1):61-65.(in Chinese)
[16] NASER E S,SAMEH N.Wavelet de-noising for IMU Alignment[J].IEEE SystemsMagazine,2004,2:32-39.
[17] 孙俊喜,陈亚珠.一种具有边缘保持特性的超声图像小波域阈值去噪新方法[J].光学精密工程,2002,10(5):429-433.
SUN JX,CHEN Y ZH.Novel speckle reduction formedicalultrasound images based on edge preservation[J].Opt.Precision Eng.,2002,10(5):429-433.(in Chinese)
EMD filtering of fiber gyro in initial alignment of SINS
WANG Yan-dong*,YANG Chun-lei,DONGWen-hui
(Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)*Corresponding author,E-mail:wyd321@126.com
In order to decrease initial alignment complexity,increase alignment precision,and minimize time consumption of alignment process,a new method of the EMD filtering is adopted for SINS initial alignment.First,based on the algorithm of EMD sift process,the IMU signal can be decomposed into a cluster of IMFs.According to the criterion of CMSEminimization,the IMU signals can be reconstructed utilizing the IMFs cluster.Then IMU noise of original signal and filtering signal can bemodeled by ARMA algorithm,respectively.Furthermore,the coarse initial alignment process is demonstrated by the physics characteristic of the earth,and the results are compared by the data non-filtering and filtering of the same IMU.Finally,the fine initial alignment of SINS is completed using non-filtering data,filtering data of IMU and SINS error model.Experimental results indicate that the precision of azimuth angle coarse alignment is 1.3°,fine alignment is 0.87mrad,and Kalman filter converge time is 200 s.
empiricalmode decomposition;fiber gyro;nonlinear filter;initial alignment;strapdown inertial system
P228 文献标识码:A doi:10.3788/CO.20150806.0933
2095-1531(2015)06-0933-09
2015-06-18;
2015-07-20
国家自然科学基金资助项目(No.51305421)
Supported by National Natural Science Foundation of China(No.51305421)
book=941,ebook=50

王延东(1985—),男,辽宁本溪人,硕士,助理研究员,主要从事导航系统设计和系统仿真方面的研究。E-mail:wyd321@126.com

董文辉(1984—),男,陕西岐山人,博士,助理研究员,主要从事飞行器设计和系统仿真方面的研究。E-mail:dwh406@126.com

杨春雷(1982—),男,吉林榆树人,博士,副研究员,主要从事飞行器设计和系统仿真方面的研究。E-mail:yangchunlei@ciomp.ac.cn

