椭圆形压力容器的非线性数值分析

杨凯晶（西安石油大学，陕西 西安 710000）

椭圆形压力容器的非线性数值分析

杨凯晶
（西安石油大学，陕西 西安 710000）

摘 要：本文采用有限元的方法对于椭圆断面压力容器进行了非线性数值分析。并用一个算例验证了非线性数值分析的可靠性，结果表明数值分析与实测结果的一致性较好，有限元分析完全可以满足工程需要。最后，通过分析得出的结论是椭圆形压力容器的应力分布是不均匀的。这个结论对于非圆形压力容器的设计有较大的参考价值和指导作用。

关键词：椭圆断面；压力容器；非线性；有限元；几何缺陷

1 引言

压力容器已经广泛应用于化工、医疗、航天、航空、核工程等众多领域。目前，压力容器正在向大型化和多参数化的方向发展，尤其是在石油化工行业。与此同时，压力容器也面临着高温、高压等更加复杂的环境。这就意味着对压力容器的设计有了新的要求，传统的圆形压力容器已经不能满足要求，对于非圆形压力容器的研究已经广泛展开。

试验应力方法、解析方法和数值方法是目前应力分析的主要方法。随着科技的发展，出现了新的应力测定法方法，比如光弹法、电测法、散斑法和全息干涉法等。其中，数值分析方法已经广泛应用于工程之中。韩敏[2]利用ANSYS有限元软件对压力容器进行了应力分析，分析结果与真实情况基本一致。马亚娟[3]用有限元的方法对压力容器的封头进行了应力分析，其数值分析与试验的误差在10%左右。

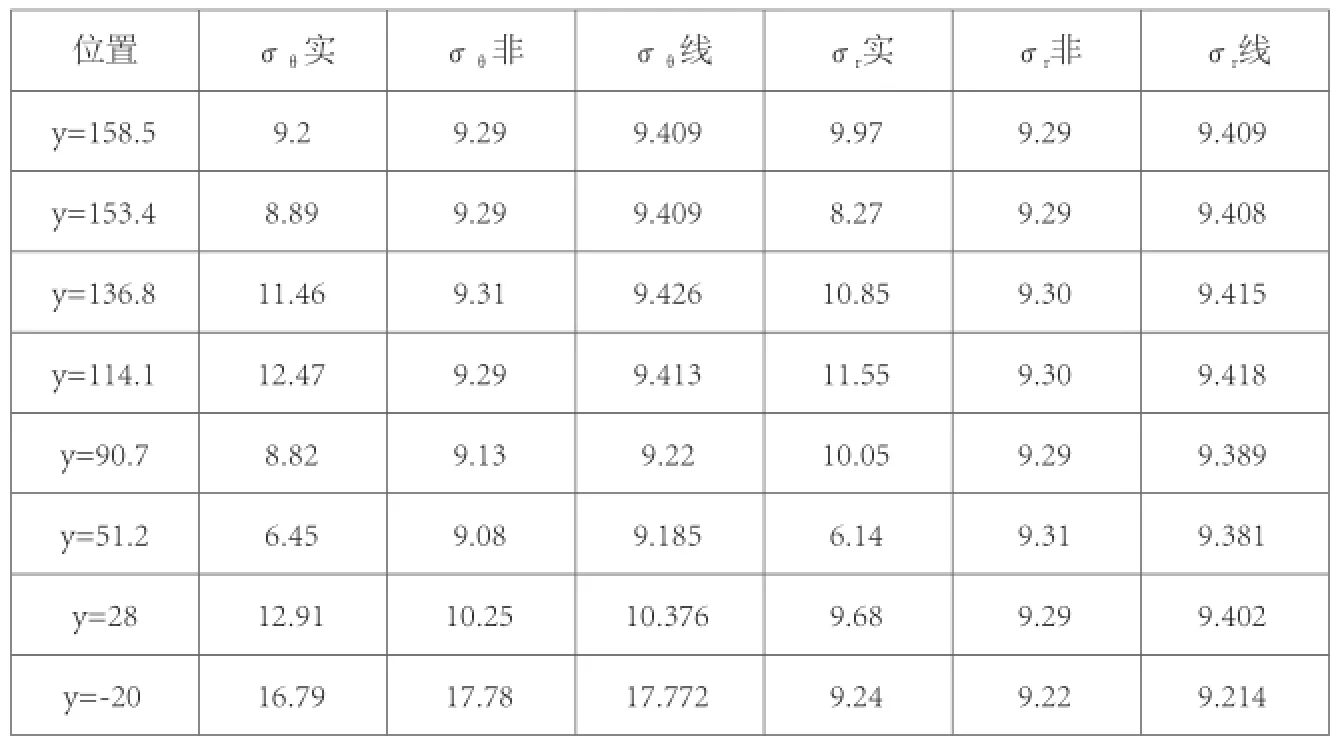
表1 有限元结果与测量值对比表

本文将采取数值分析与试验相结合的方法，利用有限元软件ANSYS对椭圆形压力容器进行应力分析，并用实验数据来验证数值分析的正确性。从而大大节约了压力容器的设计成本和设计周期。并且在线性分析的基础上进行非线性数值分析，数值分析与试验的误差在6%左右，取得了较好的一致性。

2 非线性数值分析由于制造工艺的

图1椭圆形压力容器的周向和径向应力云图

限制，压力容器在制造过程中总会存在一定的缺陷，而这种缺陷在有限元分析的建模中是难以实现的，这就会引起数值分析与实际情况的误差。

非线性数值分析是在线性分析的基础上，引入缺陷度的概念，对有限元模型施加合适的初始缺陷，再进行数值分析。缺陷度定义为设计最大误差与线弹性分析节点位移最大值的比值。

非线性数值分析的流程是在线性数值分析的基础上进行的。为了更详细的介绍非线性数值分析的流程，将其所有的步骤展开如下：

第一步：在UG中建模。

第二步：将建好的模型导入ANSYS中。

第三部：对模型施加边界条件，包括约束和载荷，需要注意载荷的方向。

第四步：进行网格划分，需要设置合适的网格尺寸，尺寸太大会引起求解精度的下降，尺寸太小会引起求解速度的下降。

第五步：进行线弹性求解。

第六步：通过后处理，得到模型节点位移的最大值，并计算缺陷度。

第七步：对模型施加合适的初始缺陷。

第八步：再次进行线弹性分析，并观察结果。

3 有限元方法的验证

马亚娟利用ANSYS对球形封头及筒体进行了应力分析，本文将采用非线性数值分析的方法对文献[3]中的封头及筒体进行分析，以验证该方法的准确性。

在ANSYS中建立球形封头及筒体的有限元模型及边界条件。筒体内径154.5mm，壁厚8mm，封头内径154.5mm，壁厚8.1mm，A端施加固定约束，限制其Y方向的位移，B端施加对称约束，使其关于X轴对称，模型内部施加1MPa的均布压力。

在模型的指定位置设置8个硬点，以观察这些位置的应力。硬点的坐标分别是：0，158.5，0；40，153.4，0；80， 136.8，0；110，114.1，0；130，90.7，0；150，51.2，0；156，28，0；158.5，-20，0。经过计算，通过后处理命令观察指定硬点的周向和径向应力。

为了说明分析的准确性，将有限元分析的结果与测量值进行对比，见表1。其中，‘σθ实’表示实测周向应力，‘σθ非’表示非线性分析的周向应力，‘σθ线’表示线性分析的周向应力，‘σr实’表示实测径向应力，‘σr非’表示非线性分析的径向应力，‘σr线’表示线性分析的径向应力，从上到下依次对比8个硬点的应力。

从表1中可以看出，除了y=51.2处的硬点，对于其他的硬点，有限元的计算结果与测量值吻合性较好，相对误差在6%左右，能够准确的进行压力容器的应力计算。而且非线性分析的结果比线性分析的结果偏小，更加接近真实值，这都是在分析中考虑了压力容器的初始几何缺陷的缘故。

4 椭圆断面压力容器数值分析

椭圆断面压力容器具有与圆形断面压力容器不同的特点和受力状态，有必要对其进行研究。本文将采用有限元的方法对椭圆断面压力容器进行应力分析，对于非圆形压力容器的进一步研究有一定的参考价值。

椭圆断面压力容器并非真正意义上的椭圆，只是近似的椭圆形。其由半径是R的大圆弧和半径是r的小圆弧组成，大小圆弧的厚度分别是δ1和δ2，其值可以相等也可以不相等，大小圆弧的圆心角分别是2θ和2φ。

本文中设置椭圆断面压力容器的具体参数如下：R=150mm，r=30mm，θ=30°，φ=60°，δ1=δ2=8mm。由于椭圆形压力容器是对称结构，本文在分析中将建立模型的1/4部分，然后施加边界条件。对模型施加对称约束，然后对模型内部施加1MPa的均布压力。

通过计算，得到了椭圆断面压力容器的周向和径向应力云图，如图1所示。从图1左半部分可以看出，压力容器大圆弧中部外侧的周向应力最大，小圆弧中部外侧的周向应力最小，表明椭圆形压力容器的周向应力分布是不均匀的。观察图1右半部分可以看出，径向应力分布方式与周向应力的分布有所不同，径向应力最大值出现在压力容器大圆弧中部外侧和小圆弧中部内侧，最小值出现在小圆弧中部外侧，径向应力的分布同样是不均匀的。

结语

椭圆形压力容器的应力分布与圆形压力容器完全不同，其沿着周向的应力大小各不相同，这对于非圆形压力容器的设计有一定的参考价值。在非圆形压力容器的设计中，根据有限元分析的结果，将应力较大的部分的壁厚加厚，将应力较小部分的壁厚适当减薄，使其应力的分配尽量均布化。如此设计，既可以保证非圆形压力容器能够承受更大的压力，又可以保证压力容器不会太笨重。

非线性数值分析考虑了压力容器在制造过程中的几何缺陷，使得数值分析的结果与真实值更加接近，有限元分析的可靠性得到了一定的提升。

但是在分析中，还会出现数值分析与实验结果不一致的地方，这是由于有限元模型与试样的不完全一致造成的，这个问题将是本文作者今后研究工作的重点。

参考文献

[1]Liu P, Xu P, Han S, et al. Optimal design of pressure vessel using an improved genetic algorithm[J]. Journal of Zhejiang University SCIENCE A, 2008, 9（09）.

[2]韩敏.利用ANSYS软件对压力容器进行应力分析[J].煤矿机械，2008，29（01）：73-74.

[3]马亚娟.压力容器的球形封头和椭圆形封头的应力测定及分析[D].西安工程大学，2014.

中图分类号：TH49

文献标识码：A