基于蒙特卡罗法的土石坝洪水漫顶风险率计算及其敏感性分析

吕弯弯，顾圣平，何 蕾，刘欣欣，赵一梦

(河海大学 水利水电学院，南京 210098)

基于蒙特卡罗法的土石坝洪水漫顶风险率计算及其敏感性分析

吕弯弯，顾圣平，何 蕾，刘欣欣，赵一梦

(河海大学 水利水电学院，南京 210098)

为了减少土石坝因洪水漫顶造成溃坝所带来的损失，详细介绍了计算土石坝洪水漫顶风险率的蒙特卡罗法模型，分析了影响土石坝洪水漫顶的主要因素为洪水、风浪、水库运行调度方式和水库特性。针对这些因素进行洪水漫顶风险率的敏感性分析，并以南方某土石坝为例进行了实例研究。结果表明：洪峰流量均值和变差系数以及最大风速的均值对土石坝洪水漫顶风险率的影响较大，洪峰流量的偏态系数和风速的均方差的影响较小；水库自身特性及洪水到来前的水库初始水位的影响也比较大。该实例计算得到的洪水漫顶风险率经与相关工程实例分析计算成果比较，表明采用蒙特卡罗法计算洪水漫顶风险率是可信的。

土石坝；洪水漫顶风险率；不确定性因素；蒙特卡罗法；敏感性分析

在我国已建成的9万多座水库大坝中，90%以上是土石坝[1]。据资料统计，土石坝洪水漫顶和坝体失稳是土石坝失事的2个主要原因。我国水库由于洪水漫顶造成的溃坝约占大坝溃坝总数的47.85%[2]，世界上由于洪水漫顶造成溃坝的比例也高达1/3[3]。因此，开展对大坝洪水漫顶风险率的研究，可为已建水库的除险加固和新建水库的设计提供科学的决策依据。

1 土石坝洪水漫顶风险率的影响因素分析

洪水漫顶是指由洪水引起的坝前最高水位超过坝顶高程或防浪墙顶高程的现象。大坝的洪水漫顶风险率是指由洪水造成的漫顶事件发生的概率。

设H表示由洪水引起的坝前最高水位，Z表示坝顶(或防浪墙顶)高程，则洪水漫顶风险率可表示为P(H>Z)。其中

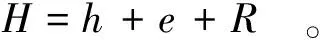
(1)

式中：h为坝前最高静水位；e为风荷载引起的风壅高度；R为风荷载引起的波浪爬高。

一般而言，坝前最高静水位h既与洪水大小有关，又与水库特性及水库运行调度方式有关，水面壅高e和波浪爬高R则主要决定于风荷载的作用。由此可见，影响土石坝洪水漫顶风险率P(H>Z)的因素主要包括洪水、风浪、水库运行调度方式和水库特性等方面的不确定性。

洪水是一种随机水文现象，分析洪水的不确定性，一般需要考虑洪水的洪峰流量、洪量和洪水历时3个方面，以及它们之间的相关性。而完整考虑这些因素，相关的分析计算就会变得很复杂。为简化起见，在土石坝设计过程中，有时可以将洪水过程简化为按洪峰流量同倍比放大典型洪水过程线得到，这时，分析洪水因素的不确定性，主要是根据历史洪水资料，研究洪峰流量的概率特性。

风浪也是一种随机现象，关于风浪的不确定性，一般需要综合考虑风速、吹程和风向等不确定性因素。为简化计算，在土石坝风浪超高的设计过程中，通常主要考虑风的最大风速和吹程，并可根据历史风资料，研究以最大风速为变量的风的概率特性，吹程则大多采用多年平均吹程。在此基础上，可进一步研究风荷载引起的水位壅高和波浪爬高的特性。

水库运行调度方式是指为满足防洪及兴利要求而制定的对入库水量进行调节的水库蓄、泄计划，其具体实施主要是控制不同时期的水库特征水位。例如，在洪水到来之前，一般将水库水位控制在防洪限制水位。但是，在水库实际运行中，由于各方面的原因，水库在洪水到来之前的水位有可能比防洪限制水位高，也可能比防洪限制水位低，这就是本文所指的水库运行调度方式的不确定性。

水库特性的不确定性，主要是指由于某种原因而导致的水库库容特性、溢洪道的泄流特性等发生变化。例如，由于水库泥沙淤积作用引起水库的水位-库容关系发生变化，使得各水位对应的库容减小，从而可能降低水库的调洪作用；由于施工质量、工程老化、维护管理不善等原因，引起溢洪道的水位-下泄流量关系与设计情况相比有所改变，使得泄流能力有所降低。

基于以上分析，采用随机模拟分析的方法对洪水不确定性和风浪不确定性对土石坝洪水漫顶风险率的影响进行研究。在此基础上，针对在统计参数分析计算过程中，由于洪水资料和风资料系列局限而引起的抽样误差等原因可能影响到随机模拟分析结果可靠性的问题，进行敏感性分析。

对于水库运行调度方式和水库特性2个因素，由于不确定性与洪水及风浪因素的随机特性是不一样的，因此，本文主要应用敏感性分析方法研究不确定性对土石坝漫顶风险率的影响。

2 洪水漫顶风险率计算的蒙特卡罗(MC)法

2.1 洪水模拟

在我国，一般认为洪峰流量服从P-Ⅲ型概率分布，其概率密度函数[4]如下：

(2)

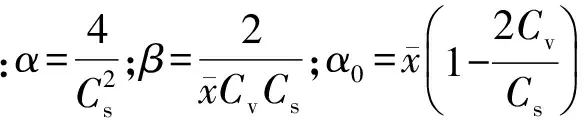
应用蒙特卡罗模拟方法[5]进行模拟分析时，可用随机数发生器产生(或经转换成为)n个具有相同概率分布(P-Ⅲ型)的随机数值，利用洪峰流量概率分布函数即可定出n个洪峰流量Qi(i=1,2,…,n)。据此，对从实测洪水资料中选出的典型洪水过程线按照同倍比法进行放大，即可得到n场洪水过程线Qi-t。

2.2 风浪模拟

最大风速的概率分布为最大值分布，一般认为符合极值Ⅰ型分布[6]，其概率密度函数如下：

(3)

风壅高度也符合极值Ⅰ型分布[6]，其均值与均方差可用一次二阶矩法求得，公式如下：

(4)

(5)

式中：W和σW意义同上； D为水库吹程，即风区长度；Hm为水域平均水深；K为综合摩阻系数，其值一般在(1.5～5.0)×10-6之间，计算时一般取3.6×10-6。

根据以上分析，由历史风速资料可以确定风速的极值Ⅰ型分布函数和风壅高度的极值Ⅰ型分布函数，应用蒙特卡罗模拟方法随机产生一组风速和风壅高度(各m个)的随机值。

另一方面，在一定风速条件下，波浪的波高是一系列随机波，其统计系列符合瑞利分布[6]，波浪爬高与波高的相关系数为1，因此波浪爬高也符合瑞利分布，其分布函数为

(6)

式中，分布参数μ与波浪爬高的均值E(x)、均方差σ(x)有如下关系：

(7)

(8)

波浪爬高的均值E(x)可以由土石坝设计规范[7]中波高公式A.1.7-1和波浪爬高公式A.1.12-1，结合给定的风速和多年平均吹程计算得到。

根据以上分析，给定一个风速，应用蒙特卡罗模拟方法进行模拟分析时，可随机产生j个符合瑞利分布的波浪爬高随机值。本文模拟了m个风速，就可以得到m×j个波浪爬高随机值。

2.3 漫顶风险率计算

首先针对通过洪水模拟得到的n场洪水的洪水过程线Qi-t，进行水库调洪计算[8]，可得到n个坝前水位变化过程hi-t，进而可得到n个坝前最高静水位hi,max。

在此基础上，对每一个坝前最高静水位，考虑风浪的随机影响，进行风浪模拟，得到m个风浪壅高度e和m×j个波浪爬高值R，代入式(1)，可得到m×j个最高水库水位H。于是，对于n场洪水，就有n×m×j个最高水库水位，比较最高库水位H与坝顶高程Z，并统计出现H>Z的次数(设为k次)，即可计算得到漫顶风险率为

(9)

3 敏感性分析

(10)

敏感系数表示的是某参数值升降1%，目标值随之升降的百分比。敏感系数越大，目标值对该因子的敏感程度越高。

对于水库运行调度方式对大坝漫顶风险率的影响，主要考虑由于洪水到来前水库水位超过防洪限制水位而引起的敏感性问题。具体分析时，可在设计资料的基础上，结合工程实际情况，设定洪水到来前的水库水位，再结合以上各模拟的洪水、风速方案，计算相应的大坝漫顶风险率，进而进一步分析漫顶风险率的变化程度。

水库特性变化对于大坝漫顶风险率的影响主要决定于与水库水位对应的库容和下泄流量随运行年限的增加而变化的程度。敏感性分析时，可在设计资料的基础上，设定对应水位的库容和下泄流量下降一定幅度，再结合以上各模拟的洪水、风速方案，计算相应的漫顶风险率，进而按式(10)求得敏感系数。

4 应用实例

4.1 工程概况

某水库位于我国西南地区，挡水建筑物为黏土心墙坝，坝高80 m，坝顶高程为2 830 m。水库正常蓄水位为2 823.2 m，汛期限制水位为2 823.2 m，死水位为2 796.0 m。该水库运用方式：洪水来临时，用闸门控制下泄流量等于来水量，水库保持汛前限制水位不变，当来流量继续加大，闸门全开，下泄流量随水位的升高而加大，流态为自由泄流。

表1 不同频率洪峰流量

该电站的设计洪峰流量Q设=1 680 m3/s(P=1%)，校核洪峰流量Q校=2 478 m3/s(P=0.05%)。坝址区实测多年最大风速的均值W=19.1 m/s和均方差σW=2.747 8 m/s，相当于8级风力，风向为西北偏西，水库多年平均吹程为15 km。

4.2 漫顶风险率计算

(1) 为简化起见，本文主要针对一定范围内的模拟洪水进行漫顶风险分析，其范围的选取满足以下2点：①由于在大坝设计阶段已经对校核洪水进行过调洪计算和风浪超高计算，并据以确定校核洪水位和坝顶高程，因此，可以认为对于洪峰流量远小于校核标准的洪水，不会产生漫顶情况；②对于远远超过校核标准的洪水认为其不会发生。据此，拟定模拟洪水洪峰流量的范围为[2 000,7 000](m3/s)。根据该水库的洪峰流量频率曲线，确定洪峰流量落在该区间的概率为0.002 9。

为计算洪峰流量在区间[2 000,7 000](m3/s)内的洪水漫顶风险率，在该区间内，通过随机模拟产生n场洪水(n=1 000)，并对每一场洪水进行水库调洪演算，可以得到1 000个坝前最高静水位。

(2) 在此基础上，对于每一个坝前最高静水位，模拟m组风速和风壅高度以及j个波浪爬高(m=100，j=100)。于是，对在该水库洪峰流量区间[2 000，7 000]范围内所模拟的1 000场洪水，总计可以得到1 000×100×100=10 000 000个最高水库水位H。统计结果显示，共有30 602个坝前最高水位超过了坝顶高程2 830 m，其中最大值2 832.3m。根据式(9)可得漫顶风险率：

(3) 由于该漫顶风险率值是针对洪峰流量落在区间[2 000,7 000]上的模拟结果求得的，而洪峰流量落在该区间的概率为0.002 9，因此，最终确定该土石坝的洪水漫顶风险率为

P′=0.002 9×3.060 2×10-3=8.874×10-6。

(11)

可见，该土石坝洪水漫顶风险率在10-6～10-5量级之间，经与相关文献[3,6,10-13]中工程实例分析计算成果比较，表明使用蒙特卡罗法计算得到的洪水漫顶风险率是合理可信的。

4.3 敏感性分析

(2) 计算基准方案的洪水漫顶风险率，其值为式(11)所求得的8.874×10-6。

(3) 给定洪水和风速的5个分析因子的一定的变动幅度，计算相应的漫顶风险率和敏感系数，结果列于表2。

从表2可以看出，对大坝漫顶风险率影响最大的是洪峰流量均值，其敏感系数约为19.46，即若洪峰流量均值增加1%，漫顶风险率随之增加约19.46%；洪峰流量的变差系数Cv的敏感系数较大；偏态系数Cs相对影响较小。风浪对土石坝漫顶风险率的影响也较显著，其中最大风速均值W影响较大，相应的敏感系数为约为8.80；而均方差σW影响很小，几乎可以忽略。

表2 洪水和风浪参数的敏感性分析

(4) 对于水库在洪水到来前的初始水位，以实际运行资料中的可能出现的汛前水位范围为2 823.2～2 823.6 m进行分析；对于水位库容关系和水位流量关系，分别以对应水位的库容和下泄流量比设计数据减小5%～20%的变动情况进行分析。经计算，相应的漫顶风险率和敏感系数结果列于表3。

表3 水库特性参数的敏感性分析

从上表可以看出，水库库容和下泄流量的敏感系数分别约为-8.36和-5.49，也就是说，若对应水位的水库库容或下泄流量减小1%，漫坝的风险率分别增加约8%和5%，可见水库特性对漫顶风险率的影响较大。由于水库初始水位的变动不宜用百分比来衡量，故不能直接得到其敏感系数，但是可以看到，水库初始水位仅上升0.2 m，就造成漫顶的风险率增加了约一半。

5 结 语

本文分析了造成土石坝洪水漫顶的风险因素，详细介绍了运用蒙特卡罗法计算土石坝洪水漫顶风险率的模型，并在此基础上对土石坝洪水漫顶因素进行了敏感性分析，结果表明:

(1) 运用蒙特卡罗模拟法计算土石坝洪水漫顶风险率的模型是有效的，结果是可信的。

(2) 洪水和风浪的特性对大坝洪水漫顶风险率均有较大影响。其中，洪峰流量均值和风速均值影响最大，洪峰流量变差系数影响次之，洪峰流量的偏态系数和风速的均方差影响最小。水库特性(库容和泄流能力)对大坝漫顶风险率的影响也不容小觑，且大坝洪水漫顶风险率对于这2个因素的敏感程度相差不大。而水库在洪水到来前初始水位的变动对漫顶风险率的影响非常显著。

因此，为控制大坝的洪水漫顶风险率及其敏感性，一方面，在水库工程设计时，应注意尽可能延长水文资料系列，以减少抽样误差，并确保洪峰流量统计参数(特别是均值和变差系数)及风速统计参数(特别是均值)推求的准确性；另一方面，在水库运行管理过程中，应高度重视严格按照调度规程，控制洪水到来前水库水位的问题；同时要注意水库特性随运行时间而变化，尤其是对应水位下库容及泄流能力的变化问题。

[1] 麻荣永.土石坝风险分析方法及应用[M].北京：科学出版社，2004: 73-89.(MA Rong-yong. Methods of Analysing Earth-rock Dam and Their Applications[M]. Beijing: Science Press, 2004: 73-89. (in Chinese))

[2] 解家毕，孙东亚. 全国水库溃坝统计及溃坝原因分析[J].水利水电技术，2009，(12) ：124-128. (XIE Jia-bi, SUN Dong-ya. Statistics and Causes of Dam Collapse in China[J]. Technologies of Water Conservancy, 2009, (12): 124-128. (in Chinese))

[3] 李清富，龙少江. 大坝洪水漫顶风险评估[J].水力发电，2006，(7) ：20-22. (LI Qing-fu, LONG Shao-jiang. Risk Assessment of Dam[J]. Hydropower, 2006，(7) ：20-22. (in Chinese))

[4] 詹道江，徐向阳，陈元芳. 工程水文学[M].北京：中国水利水电出版社，2010: 100-200. (ZHAN Dao-jiang, XU Xiang-yang, CHEN Yuan-fang. Engineering Hydraulics[M]. Beijing: China Water Power Press, 2010: 100-200. (in Chinese))

[5] 赵经华，王长新.用蒙特卡罗法进行泄洪风险分析[J]. 东北水利水电，2005,(10): 1-3.(ZHAO Jing-hua, WANG Chang-xin. Analysis of Flood Discharging Risk with Monte-Carlo Method[J]. Water Resource & Hydropower of Northeast China, 2005,(10): 1-3. (in Chinese))

[6] 李其军，陈肇和. 土石坝漫坝风险理论与应用[M].北京：中国水利水电出版社，2008：16-24. (LI Qi-jun, CHEN Zhao-he. Theory and Application of Earth-rockfill Dam[M]. Beijing: China Water Power Press, 2008: 16-24. (in Chinese))

[7] SL274—2001，碾压式土石坝设计规范[S]. 北京：中国水利水电出版社, 2001.(SL274—2001, Design Code for Rolled Earth-rock Fill Dam[S]. Beijing: China Water Power Press, 2001. (in Chinese))

[8] 顾圣平，田富强，徐得潜. 水资源规划及利用[M].北京：中国水利水电出版社，2009: 111-141. (GU Sheng-ping, TIAN Fu-qiang, XU De-qian. Planning and Utilization of Water Resources[M]. Beijing: China Water Power Press, 2009: 111-141. (in Chinese))

[9] 周 立. 敏感性分析法在企业利润规划中的运用[J].四川行政学院学报，2002，(5)：78-80. (ZHOU Li. Application of Sensitivity Analysis to Enterprise Profit Planning[J]. Journal of Sichuan Administration College, 2002，(5)：78-80. (in Chinese))

[10]MO Chong-xun, LIU Fang-gui, YU Mei,etal. Risk Analysis for Earth Dam Overtopping[J]. Water Science and Engineering, 2008, 1(2): 76-87.

[11]ERDIK T J, DURICIC P. The Probabilistic Assessment of Overtopping Reliability on Akyayik Dam[J]. KSCE Journal of Civil Engineering, 2003, 17(7): 1810-1819.

[12]MARENGO H, ARREGUIN F I, ALDAMA A A,etal. Case study: Risk analysis by Overtopping of Diversion Works During Dam Construction: The La Yesca Hydroelectric Project, Mexico[J]. Structural Safety, 2013, 42(3): 26-34.

[13]LAVE L B, BALVANYOS T. Risk Analysis and Management of Dam Safety[J]. Risk Analysis, 1998, 18(4): 455-462.

(编辑：陈绍选)

Calculation and Sensitivity Analysis of Risk Probability of Earth-rockDam Overtopping Caused by Floods Based on Monte-Carlo Method

LV Wan-wan, GU Sheng-ping, HE Lei, LIU Xin-xin, ZHAO Yi-meng

(College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China)

The detailed process to calculate risk probability of earth-rock dam overtopping caused by floods based on

Monte-Carlo Method was presented in this paper. Factors affecting the risk probability, inclusive of flood, wind wave, reservoir scheduling and reservoir features were deeply analyzed and sensitivity analysis for these factors was conducted. An earth-rock dam in south China was taken for example. Results reveal that the mean value of peak flow, the coefficient of variation, as well as the mean value of maximum wind speed have large impact on the risk probability; whereas the coefficient of skewness and the mean wind speed variance have little effect. Besides, the reservoir characteristics and the initial water level before flood also have considerable influence on the risk probability. By comparing the calculated results with engineering analysis results, we conclude that it’s reliable to calculate the risk probability of earth-rock dam overtopping by using Monte-Carlo method.

earth-rock dam; overtopping risk probability; uncertain factors; Monte-Carlo method; sensitivity analysis

2014-09-16；

2014-10-16

国家“十二五”科技支撑计划项目(2013BAB06B01)

吕弯弯(1990-)，男，河南洛阳人，硕士研究生，主要从事水利水电规划与水利经济方面研究,(电话)15195872328(电子信箱)793145268@qq.com。

顾圣平(1957-)，男，江苏泰州人，教授，主要从事水利水电系统规划等方面的研究，(电话)13951893043(电子信箱)spgu@hhu.edu.cn。

10.3969/j.issn.1001-5485.2015.05.009

2015,32(05):48-52,56

TV641

A

1001-5485(2015)05-0048-05