桥式起重机吊装过程动力学分析及最大动力响应解算
李艳娇1,李瑞敏
(1.沈阳建筑大学建筑设计研究院,辽宁 沈阳 110015;2.沈阳机床(集团)有限责任公司设计研究院,辽宁 沈阳 110142)
·建筑与土木工程·
桥式起重机吊装过程动力学分析及最大动力响应解算
李艳娇1,李瑞敏2
(1.沈阳建筑大学建筑设计研究院,辽宁 沈阳 110015;2.沈阳机床(集团)有限责任公司设计研究院,辽宁 沈阳 110142)
吊钩桥式起重机吊装过程中的最大动力响应发生在货载起吊离地和全速下降制动2个瞬间。本文对这2个瞬间动力过程进行详细研究,包括影响因素分析及力学、数学模型的建立等,并用MATLAB软件对一桥式起重机吊装过程的最大动力响应进行解算,解算结果可以作为吊具选用及强度设计的依据。
桥式起重机;动力学分析;最大动力响应
车间和仓库中常用吊钩桥式起重机来起吊和移动重物,所以经常需要选用或自制一些吊具,重物上也会预留专门的位置以便吊装。无论是吊具的选用和设计,还是重物上吊装位置的预留,都需要知道重物在吊装过程中的最大动力响应,这也就是本文所要研究的问题。吊钩桥式起重机的基本组成及运行原理是这样的:大车(桥架)在车间两侧的轨道上纵向运行,小车在大车的导轨上横向运行;绳索的一端固定在小车上,然后在下端的动滑轮和上端的定滑轮之间缠绕若干次,另一端卷绕在辊筒上,辊筒支撑在小车上在电机经由减速器带动下转动以提升和下放重物,电机和减速器之间装有制动刹车。这样,重物就可以被吊放到车间跨度空间内的任何位置[1]。很明显,系统的最大动力响应发生在货载起吊离地和全速下降制动2个瞬间,所以下面分别对这2个短暂的动力过程进行分析。
1 起吊离地瞬间的动力学分析
1.1阻尼的影响
这里的阻尼类型主要是起重机各构件间的摩擦阻力和各构件的材料内阻。阻尼机制比较复杂,较难用数学公式准确描述,即使可以准确描述,也因是非线性的,将其引入动力问题研究的微分方程中后,微分方程的求解也会非常困难。通常的方法是利用能量原理将其转换成与速度成正比的黏滞阻尼力来研究。我们初步把起重机看成一个单自由度弹簧质量阻尼系统来定性的分析。单自由度弹簧质量阻尼系统的阻尼比为
(1)
其中:c为黏性阻尼系数;m为单自由度系统的质量;ω为单自由度系统的固有频率。对于起重机的金属结构,一般ζ=0.008~0.05,其中焊接结构取ζ=0.008~0.01,铆接结构取ζ=0.015~0.05。可见,它是阻尼较小的欠阻尼系统[2]。由于本文主要研究货载起吊离地和全速下降制动2个瞬间的最大动力响应,为保守起见,这里将阻尼忽略不计。
1.2动力过程分析及模型的建立
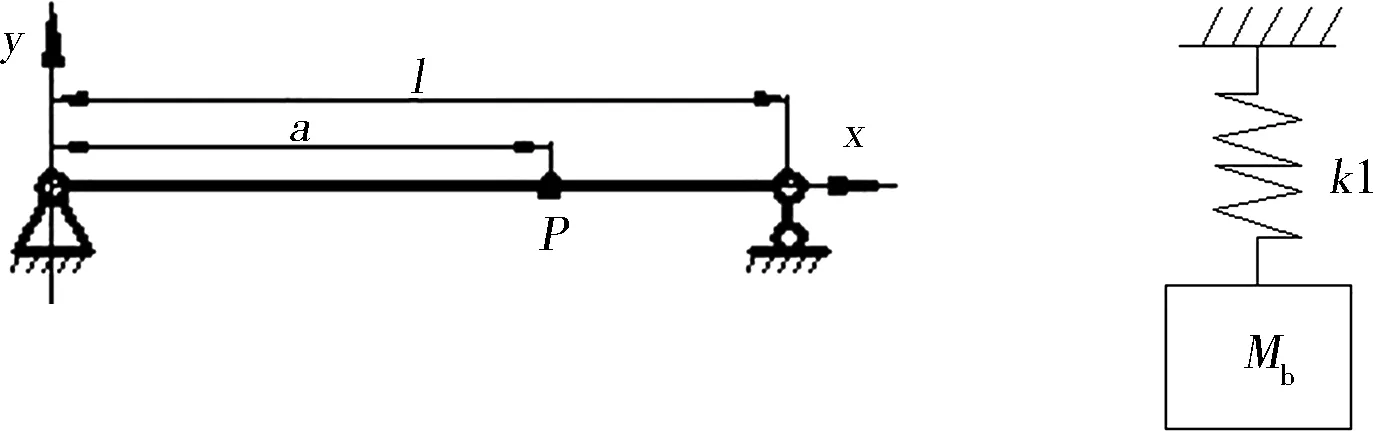
1.2.1 大车模型的建立
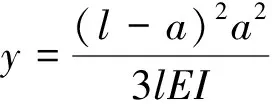
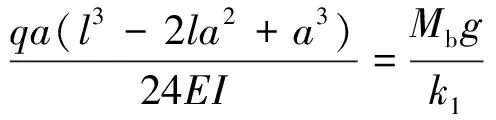
解得

(2)
显然,起吊点不同,k1和Mb的值也不同,跨中位置它们的值都最小,距离跨中位置越远,它们的值越大。
(a) (b)
1.2.2 起重机系统模型的建立
整个起吊过程可以分成3个阶段[1-6]。
第1阶段:绳子是松弛的,起吊传动系统在空运转,绳子逐渐被卷绕到辊筒上,直到绳子收紧并开始受力时为止。这一阶段吊钩在上升,桥架和货载m2还处于静止状态。此阶段结束时吊钩的速度取决于绳子的松弛程度和起吊驱动控制策略等,有可能已经达到了起吊额定速度v0,也有可能还没有达到起吊额定速度v0。
第2阶段:从绳索开始受力到绳索弹性张力等于货载重力G2=m2g为止。根据引言中所述的起重机起吊原理和1.2.1节中的大车力学模型可得这一阶段的系统力学模型如图2(a)所示。图中,m1为大车在货载起吊点的等效质量Mb与小车质量mt之和,即m1=Mb+mt。此模型可以进一步简化为图2(b)所示的力学模型,图中n表示动滑轮索槽个数,v表示吊钩的起升速度,k2表示滑轮钢绳系统的刚度系数。重物起吊离地的整个动态过程中,v是导致弹簧被拉伸的主要原因。为了简化分析,我们假设第1阶段结束时吊钩的起升速度已经达到额定起升速度v0。通过下面的分析易知,这样分析相对保守,更趋安全。


(a) (b)

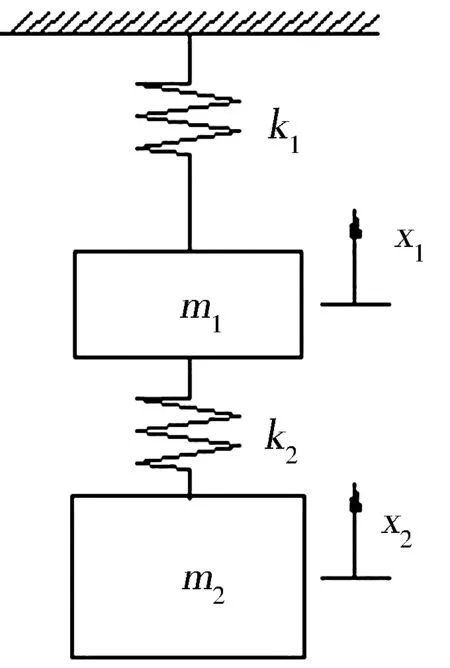
(a) (b)
图2 桥式起重机力学模型
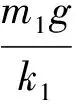
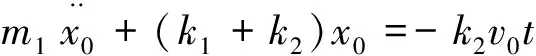
(3)
用MATLAB中的dsolve函数解此微分方程得

(4)
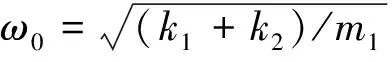
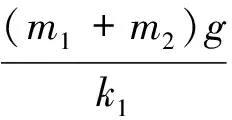
(5)
设x2=y1-v0t,微分方程(5)变为:
(6)
相应地,系统动力学模型变成如图2 (d)所示。无论从数学模型还是力学模型均可以看出此时的系统是一个二自由度无阻尼自由振动系统。下面确定该方程组的初始条件。第2阶段的末了状态即是第3阶段的初始条件,可由式(4)求得,不过需要知道第2阶段运动历时t1。由第2阶段末绳索的弹力等于货载m2的重力知t1可由下式解得
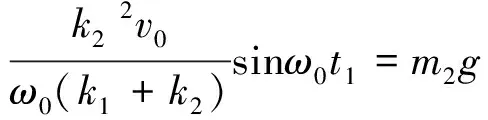
(7)
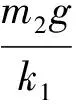

(8)
m1的初速度为
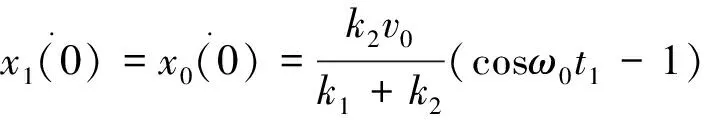
(9)

此时x2便可由式(6)求解。

2 全速下降制动瞬间的动力学分析
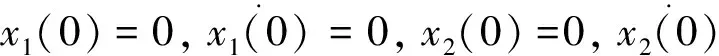
3 最大动力响应的MATLAB解算
我单位新厂房一起重机,跨度l=13.5 m,桥架质量mb=14 700 kg,小车质量mt=3 800 kg,桥架跨中刚度k1=1.2×107N/m,吊钩下放到地面时滑轮组刚度k2=9×106N/m,额定起升速度v0=8.4 m/min。下面用MATLAB计算其在跨中点吊装m2=20 000 kg重物时的最大动力响应,从而为吊具的选择及强度设计提供依据。
3.1起吊离地瞬间的最大动力响应
跨中点

将参数代入式(7)得
720 000t1+13 429sin40.211 2t1=196 000。
用MATLAB中的solve函数解此超越方程得t1=0.287 8 s。
由式(8)、(9)计算式(6)的初始条件得
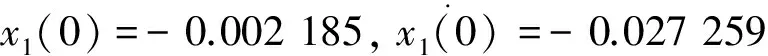
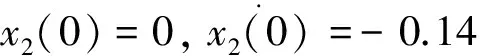
将各参数代入式(6),用MATLAB中的dsolve函数[7]解微分方程组并化简得:
x2=0.000 6cos(42.9t)-0.000 28sin(42.9t)-
0.000 6cos(15t)-0.008 6sin(15t);
0.135cos(15t)+1.935sin(15t)。
用fplot函数[7]绘制加速度曲线:
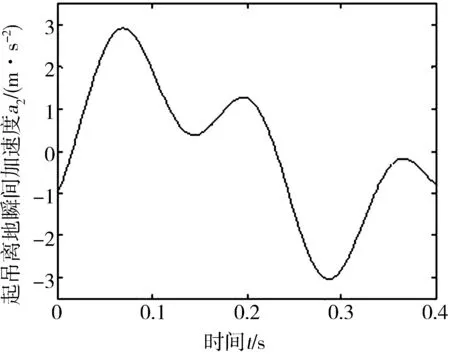
图3 起吊离地瞬间加速度-时间曲线图
找出最大加速度
a2max=2.91m/s2。
动载系数及重物处的最大动力响应为:
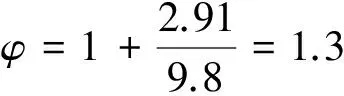
Fmax=1.3m2g。
3.2全速下降制动瞬间的最大动力响应
重物全速下降到接近地面时制动,利用第2节中所述的初始条件,将各参数带入式(6),用MATLAB中的dsolve函数解微分方程组并化简得:
x2=-0.00045sin(42.9t)-0.008sin (15t);

用fplot函数绘制加速度曲线。
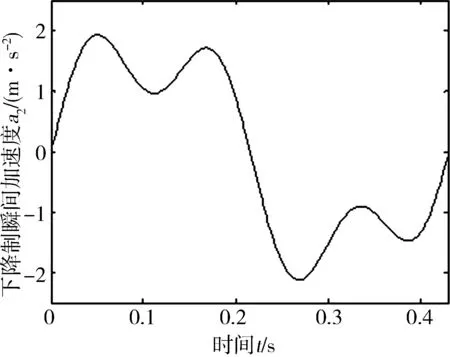
图4 下降制动瞬间加速度-时间曲线图
找出最大加速度为
a2max=1.92m/s2。
动载系数及重物处的最大动力响应为:
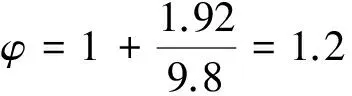
Fmax=1.2m2g。
需要注意的是,若重物在距地较高的位置下放制动时,由于绳索短,k2较大,所以最大动力响应也较大。
4 结束语
本文以研究吊钩桥式起重机吊装过程中的最大动力响应为研究目的,对起吊离地和下降制动2个瞬间的动力过程进行了详细分析,并用MATLAB对一具体起重吊装过程的最大动力响应进行了解算。分析过程对类似问题的研究具有参考意义,解算结果可以作为吊具选用或强度设计的依据。分析过程中忽略了电机到辊筒间动力传动系统的柔性等次要影响因素,分析结果相对保守,更趋安全。
[1]周诗洋.冶金桥式起重机静动态特性和疲劳寿命分析[D].武汉:武汉科技大学,2011.
[2]胡宗武,阎以诵.起重机动力学[M].北京:机械工业出版社,1988:9,41-47.
[3]高继勇,王金诺.桥式起重机动态分析与优化设计[J].机械设计,1994(6):13-17.
[4]程文明,邓斌,王金诺.小车架为弹性结构时门式起重机的动态特性研究[J].西南交通大学学报,200l,36(2):144-148.
[5]孙民,王志远,付为刚.桥式起重机起吊过程的动力学分析[J].设计与研究,2010,37(5):12-14,77.
[6]张玉琴,冯山岭,张淑红.桥式起重机的动力学模型与仿真计算[J].重型机械科技,2005(3):1-4
[7]陈杰.MATLAB宝典[M]. 3版.北京:电子工业出版社,2007:267-298.
[8]机械工业部北京起重运输机械研究所,城乡建设环保部长沙建筑机械研究所.GB3811—83 起重机设计规范[S].北京:国家标准局出版社,1983.
(编校:叶超)
DynamicsAnalysisandMaximalDynamicResponseCalculationoftheBridgeCraneintheHoistingProcess
LI Yan-jiao1, LI Rui-min2
(1.ArchitectureDesignandResearchDepartment,ShenyangJianzhuUniversity,Shenyang110015China;2.DesignandResearchDepartment,ShenyangMachineTool(Group)Co.,Ltd.,Shenyang110142China)
The maximal dynamic response in the hoisting process of the bridge crane occurs at the two moments of lift-off and braking during full speed descent process. The two dynamic processes were researched detailedly, included the influence factors analysis,the dynamics and mathematics model establishment, etc. Then the maximal dynamic response in the hoisting process of one bridge crane was calculated in MATLAB integrated devolopment enviroment, the result could be the warrant of the hoisting tool selection and design.
bridge crane; dynamics analysis; maximal dynamic response
2014-01-07
李艳娇(1982—),女,工程师,硕士,主要研究方向为工业与民用建筑结构设计及工程力学分析等。
TH215
:A
:1673-159X(2015)04-00109-04
10.3969/j.issn.1673-159X.2015.04.022

