极限无缝隙论(续)


【关键词】极限可以表示为、数列的上升趋势的极大限制值、数列下降趋势的极小限制值。
【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089(2015)03-0220-03
关于数学极限定义的发展历史,北京大学数学科学学院一年级目前使用的课本数学分析(第一册)的31面这样写道:“……,其实,给出其精确的定义并非一件易事,经过众多数学家的不懈努力和不断探索,直到19世纪才有了数学上的如下定义:”这里所说的如下定义就是当前世界上各大学理工师范财经等专业所用的数学分析课本里使用的极限定义。
从19世纪以来,在世界各大学已用了一、二百年了,对于这个传统性定义,师生们都觉得难教难学,传统性定义词句叙述别扭。而今我用极限无缝隙论,用极限表示数列上升趋势里的极大限制值、下降趋势里的极小限制值,引入极限概念,并形象的给出其定义。
请看如下:
(一)“数列f(n)无缝隙靠近于某常数A”及其检验方法。
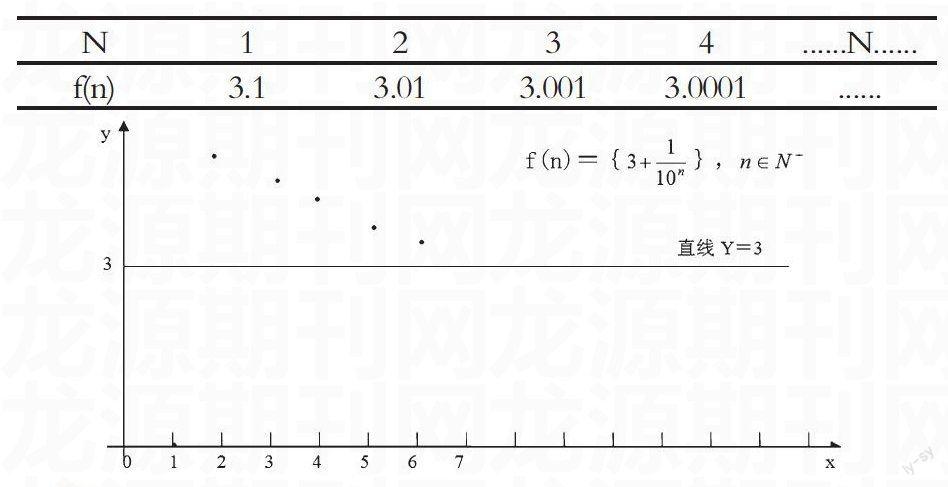
请看例题1:比较数列f(n)={3+ }和常数3之关系。
再看例题2,比较数列f(n)={4+ }和常数3之关系。
解:通过画图,可以看出数列f(n)随着项数n的增大,也是越来越靠近于数3的(你总不能说f(n)越来越远离于直线y=3的吧)但是这种靠近和例题1的靠近是截然不同的。
所以对于任意小的L>0,数列f(n)= {3+}从第[lg]项起以后所有的一切项使得数列f(n)与数3的距离都小于L,简单来说,这就是任意小的距离L,都存在着数列f(n)={3+}的项,因而数列f(n) ={3+}与数3不存在任何空隙,不存在任何缝隙。也就是说数列f(n)是无任何间隙的、是无缝隙的靠近于常数y=3的。
这样,从以上我们便得出考查数列f(n)是无缝隙的靠近于某常数A的方法是:用从数列f(n)到直线y=A的距离小于任意小的正数L的不等式,|f(n)-A| (二)对极限原由的探索:极限可以理解为数列f(n)上升趋势里的极大限制值,下降趋势里极小的限制值。 我们考查如下几个数列: 例题1、数列f(n)={3-}n∈N+,a 1=2.9 , a2=2.99 , a3=2.999 , a4=2.9999, a5=2.99999,a6=2.999999……,变化趋势是逐渐上升的,f(n)无缝隙的靠近于3,但不等于3,极大限制值是3。简称极限是3。 例题2、数列f(n)={3+ }, n∈N+ ,a1=3.1 , a2=3.01 , a3=3.001 , a4=3.0001 , a5=3.00001, a6=3.000001变化趋势是逐渐下降,无缝隙的靠近于3,但又不等于3,极小限制值是3。简称极限是3。 f(n)的值忽而大于3,忽而小于3,在这里数列f(n)存在着两个变化趋势。一个是在直线y=3的上方是下降趋势,在直线y=3的下方是上升趋势,在这两个趋势里,在下降的趋势下,y=3是f(n)的极小限制值。在上升的趋势下,y=3是数列f(n)的极大限制值。综合以上常数y=3是数列f(n)的下降趋势的极小限制,f(n)上升趋势的极大限制,简称为极限。像上面数列f(n)的极限是3,f(n)不外乎是从直线y=3的上(下)方一侧无缝隙的靠近于y=3的,也可能从直线y=3的上、下两侧同时无缝隙的靠近y=3的,别无他样了。就这样它们都被统一在下降(上升)趋势里的极小(大)限制里了,简称极限。它们都被统一在极限概念之下了。(至于一般数列f(n)或函数的极限是A,也是同这一样。) (三)f(n)极限是A;数列f(n)无缝隙靠近于A;|f(n)-A| 上面引入了极限的概念。例如数列f(n)={3+}的极小限制值是3,f(n)的极限是3。数列f(n)的极限是3也好,数列f(n)无缝隙的靠近于3也罢,它们都是在数列f(n)的项数n无限制的增大时才呈现出的一种景象,这两个景象是一致的,是相同的,是等价的。 从而一般的说来,“数列f(n)的极是A”;“数列f(n)无缝隙的靠近于A”,“不等式|f(n)-A| (四)极限的定义(描述性) 由于数列f(n)的极限是A和数列f(n)无缝隙地靠近于常数A,二者是等价的,所以我们可以引用极限的定义如下: 已知数列f(n),又已知一个常数A,如果f(n)随着项数n的无限制增大,f(n)无缝隙的靠近于常数A,那么常数A就叫做数列f(n)的极限。这个描述性定义,只是用于理解极限的概念之用,但不能参于算式的计算,所以还必须有极限严密性的定义。 (五)数列f(n)梁齐天极限的(严密性)定义 由于“数列f(n)的极限是A”和“对于任意小的正数L,|f(n)-A| 已知数列f(n),n∈N+,又已知一个常数A,若对于任意小的正数L,都能从f(n)与数A的距离|f(n)-A|小于L的不等式|f(n)-A| f(n)的极限是A,就称数列f(n)收敛于A,若A不存在,则称f(n)发散,或称无极限。
(六)极限的几何解释
所以从第[lg ]项起以后所有各项皆隐藏在这个“L”的距离里,因而“L”不是空隙了。这样f(n)与数3不存在什么空隙了。现在我们进一步讨论无缝隙靠近的情况。
我们可以再令代入到n>[lg ]里去,就是分数的母子一颠倒,摇身一变便成了n>lg1000=3, n>lg10000=4, n>lg1000000=6,……n>10000……,这就是说从第3项起、第4项起、第6项起,……第一万项起……以后,所有一切的项都有|3+ -3|<,|3+ -3|<,|3+ -3|<……;|3+ -3|<……,成立。
也就是说从第3项起、第4项起、第6项起,……第一万项起,……以后所有各项,所有的一切项都统统地有序地被逼近到直线y=3上、下两旁,但是就不能触碰落到直线Y=3上,(读者自己可以证明)。数列f(n)之这些项被逼近在以直线y=3上、下两旁,(对于数列f(n)= {3+}只在y=3上旁,数列f(n)= {3-}只在y=3下旁)被逼近在一个以直线y=3为中轴线、向上、向下各延伸L个单位,总宽为2L,长度为足够长的长方形、条带形里,被覆盖、被关闭在宽度为2L,宽度无限制地变窄的条形长带里,f(n)被有序地,无限制地被逼近在直线y=3之上、下方,但又不能触碰到直线y=3,就这样被极其严格的限制着,这是一个非常奇怪而又有趣的景象,(取这话前面的那个“极”字,取这句话后面的那个“限”字,故名曰“极限”,因而数3就叫作数列f(n)=3+ 之极限。因而此处也可以作为引入极限的定义),以上就是极限的几何解释。
(七)梁氏极限定义与传统极限定义的对比
①极限是数列(或函数)f(n)下降趋势里的极小限制、上升趋势里的极大限制,取极小限制里的“极”字,取限制里的“限”字。故名叫做“极限,这样很贴切、很自然而然的。
②无缝隙靠近比无限制靠近更形象。这个纯朴而通俗的词语形象的讲明了极限这个概念,而传统性定义里就没有形象的讲明极限的概念。
③现在使用的传统性极限定义是“……,总存在正整数N,使得当n>N时不等式|f(n)-A|<ε都成立……”。你看词句多么别扭。这里的大N怎么确定存在呢?怎么找呢?原传统定义里没有说明。而梁齐天极限定义开门见山地明白指出从解|f(n)-A|<ε着手,去解这个不等式,“解”被解出来了,那大N就自然而然地跳出来了,这多么顺畅和轻松呀,而解不等式又是学生们在此前经常接触和熟练使用的解算工具,从而使“极限”变成了一个通俗易懂易操作的课题。
其余与“极限无缝隙论“相同。

