再论物体的速度究竟是多少*
王 鹏 李 冰 杨培军
(安徽省阜阳市界首中学 安徽 阜阳 236500)
1 问题的提出
有不少教师发文讨论如下问题[1]:如图1所示,物体A,B以相同的速率v下降,物体C以速率vx上升,当绳与竖直方向夹角为α时,则
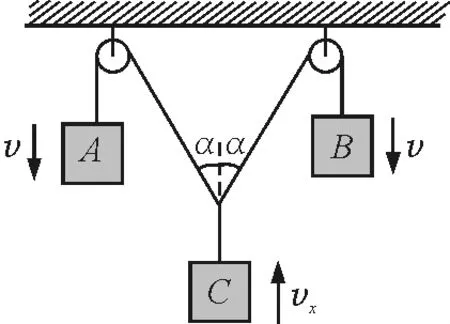
图1
常见的解法如图2和图3所示,结果分别为vx=那么究竟哪种解法正确呢?下面从几个方面进行详细剖析.
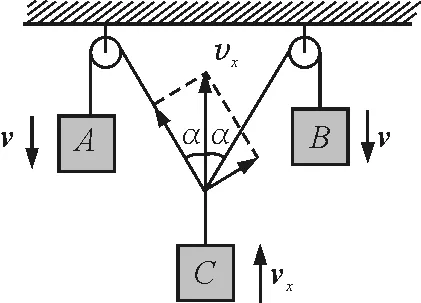
图2
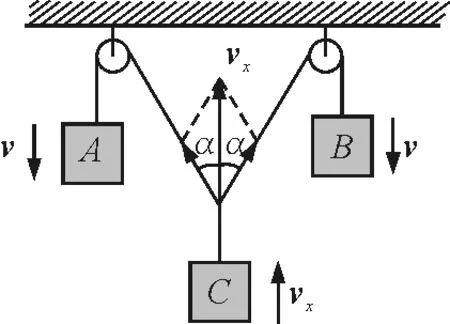
图3
2 相对运动与运动的合成与分解的区别
有些教师在分析上述问题时将小船渡河模型与之类比[2],但实际上这是两类完全不同的运动,并不能类比.小船渡河模型属于相对运动问题,而上述问题和拉船模型一样,属于运动的合成与分解问题.
对于同一物体,选择的参考系不同,其运动情况一般不同,速度自然也不同,那么各速度之间存在什么关系就属于相对运动问题,其规律为vAC=vAB+vBC,其中3个速度分别为物体A相对物体C的速度,物体A相对物体B的速度,物体B相对物体C的速度.下面来看小船渡河模型.水流速度v1是水相对岸的速度,船在静水中的速度v2是船相对水的速度,船的合速度v实际是船相对岸的速度,且v=v1+v2.
从以上分析可以看出,相对运动问题是研究同一物体在不同参考系间的速度变换关系,而运动的合成与分解则与之完全不同,它研究的是同一物体在同一参考系中的速度合成关系,其实质是矢量的合成与分解,拉船模型即属于这类问题.以地面为参考系,船(绳子末端A点)实际的运动为由A到B,将位移分解,如图4和图5所示除以时间,即得到v=v1+v2,由此即可认为绳子末端A点同时参与两个分运动:A到C,C到B,速度分别为v1和v2,其中3个速度均以地面为参考系,与小船渡河模型不同.
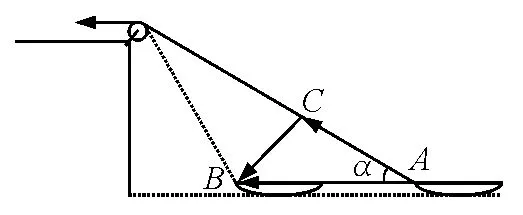
图4
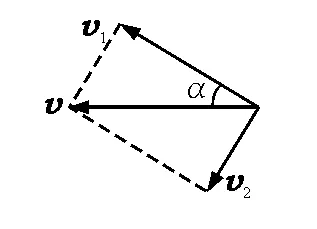
图5
3 等效替代原则
图1中给出了3个速度,有些教师便不假思索地认为它们是合速度与分速度的关系.但实际上未必,需要仔细分析.在分析时要注意等效替代原则,即所有分运动的共同作用效果必须与合运动的作用效果相同,否则便不是分运动与合运动的关系.
按照这个原则去分析拉船模型(图4,图5),可以发现,A点的速度v产生了两个效果:一个使A点与滑轮之间的绳子长度以速度v1缩短,另一个使该段绳子以速度v2绕滑轮顺时针转动,如果A点同时以v1和v2速度运动,可以产生完全相同的效果,因此v1和v2确实是速度v的分速度.
下面来分析图1问题的两种解法.图1中的问题要比拉船模型复杂,因为左右两根绳子的末端连接在一起,每一个速度会同时对两根绳子产生作用效果.在图2中,当3绳的结点以速度vx上升时,由图1可知,其作用效果是使左右两根绳子结点与滑轮间的部分长度以速度v缩短,同时使该部分绳子以速度v′(大小未知)分别绕滑轮转动.如果速度vx确实可以按照图2分解,那么两个分速度对左右两根绳子的作用效果应与速度vx作用效果相同,矢量图如图6所示.
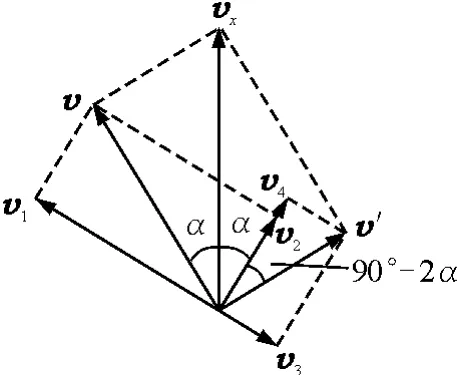
图6
根据图6,有
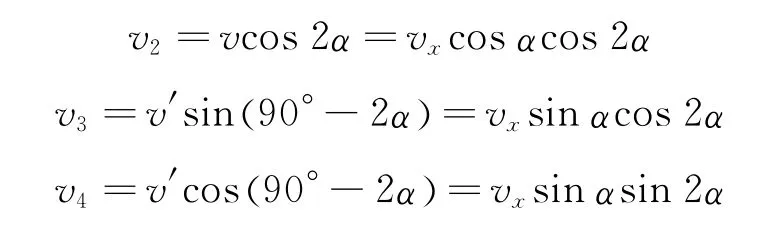
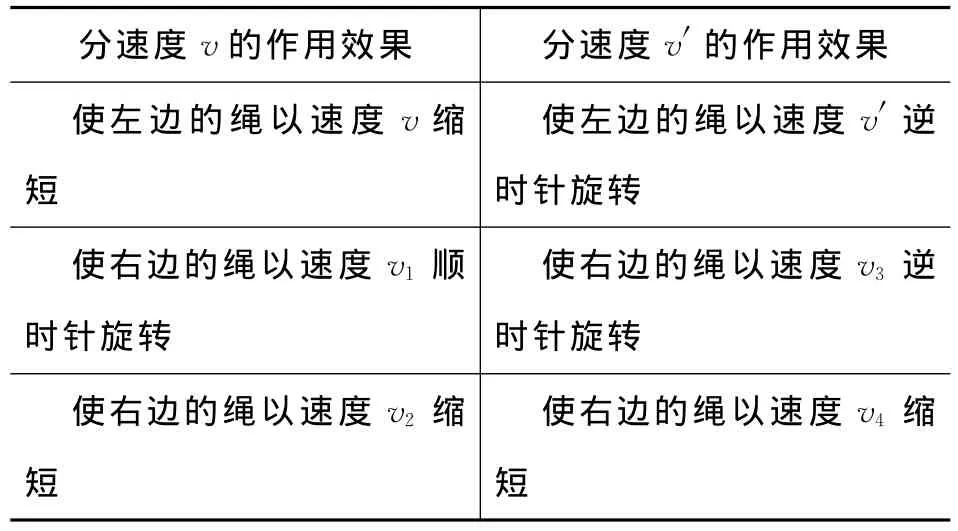
表1 分速度的效果
因此右边的绳缩短的速度为
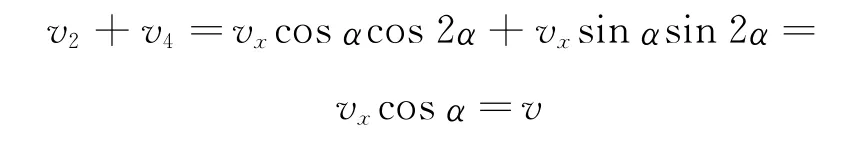
顺时针旋转的速度为
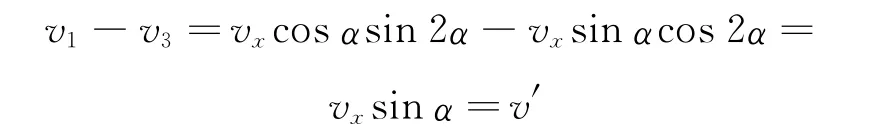
与速度vx作用效果完全相同,因此图2解法正确.按照图7分解也正确,但按照图8分解则不对.图8实际上是简单套用了拉船模型的结论,却没有注意到左右两根绳子连接在一起,互相牵制,实际上图8中4个分速度的合速度是2vx.
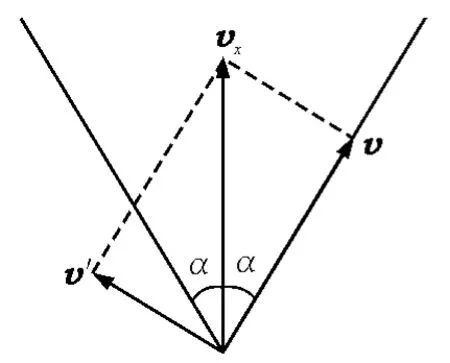
图7

图8
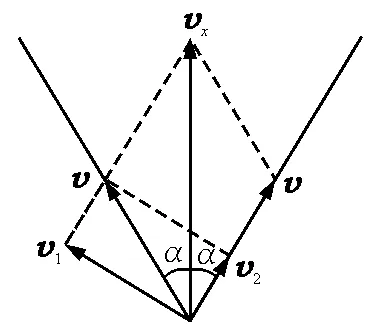
图9
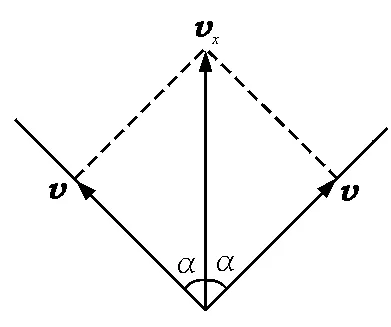
图10
4 谨防错觉误导我们
经过上面的分析发现图3的解法错误,那么为什么会产生这种错误的解法呢?笔者认为可能是错觉误导了我们.图3中滑轮与结点之间的绳子好像沿绳子方向运动,所以物体C的速度就是这两个速度v的合速度,就类似图11力的合成一样.但是这部分绳子速度是沿绳子方向吗?
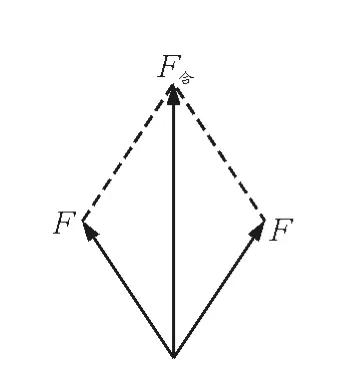
图11
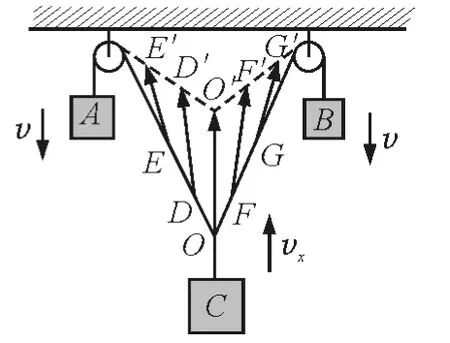
图12
从图12可以发现,滑轮与结点之间的绳子运动情况很复杂,其速度方向既不沿绳子,也不是竖直向上.绳上每一点的速度和结点O类似,既有沿绳方向的分速度v(该速度各点相同),又有垂直于绳的分速度v′(该速度各点不同,与到滑轮的距离成正比,v′=ωL),因此与图11不能类比.
在分析图3时,有些教师提出如下问题[3]:博尔特百米跑时间约为10s,速度约10m/s,那么两个博尔特拉着你跑,你的速度应为两个10m/s的合速度即20m/s,所以你应能跑出5s的百米成绩,这个看法正确吗?答案显然是否定的,然后与图3类比,即得出图3的解法不正确这个结论.
问题是我们能这样类比吗?两个博尔特拉着你跑,3人速度方向一致,与图12方向明显不同,因此不能这样类比.如果要类比应与图13类比.
下面分析图13,物体C被两根绳子拉着运动,速度是2v吗?
这个问题可以把它看做图2中α=0的特殊情况进行处理,也可以和 “两个博尔特拉着你能跑出5s的百米成绩吗”这个问题进行类比,很容易看出速度并不是2v.那么速度是2v这个错误答案是如何产生的呢?
我们来深入分析得出这个错误结果的过程:物体C同时参与两个分运动,一个跟随左边绳子向上运动,速度为v,另一个跟随右边绳子向上运动,速度也为v,因此合速度为2v.但是从图14可以看出,在一段时间内,两个分运动初末位置、位移、速度均相同,其实是同一个运动,因此物体C的速度并不等于2v,而是v.
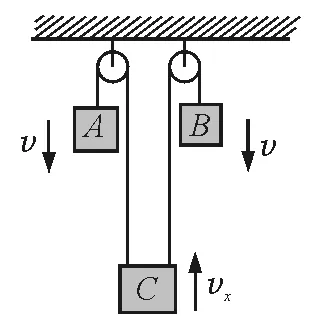
图13
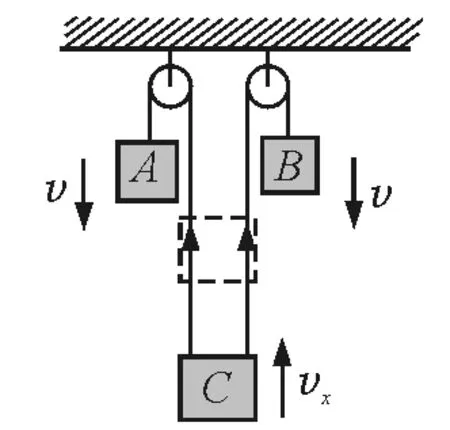
图14
再来分析图15的例子.一平面内有两直线AB和CD,相交α角,若直线AB以速度v1在平面内沿垂直于AB的方向移动,直线CD以速度v2在平面内沿垂直于CD的方向移动,求两线交点P的速度.先来分析学生的错误解法.很多学生认为P点速度就是v1和v2的合速度,究其原因,学生很可能误以为交点P是两直线上的固定点(譬如中点),然后跟着两直线一起运动,具有两个分速度v1和v2,如图16所示.

图15
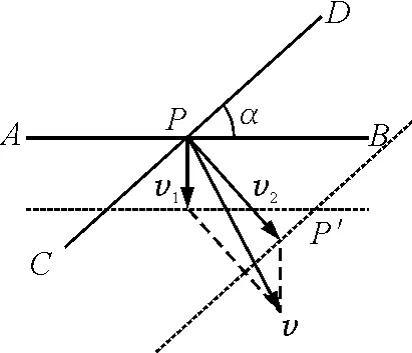
图16
然后得出P点速度就是v1和v2的合速度这个错误的结论,这显然是因为没有理解交点产生的原因而产生的错觉.实际上交点在杆上的位置是不断变动的,P′才是两杆的交点,P点速度的方向沿PP′方向(图17).

图17
沿PB方向位移为
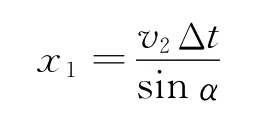
沿PC方向位移为
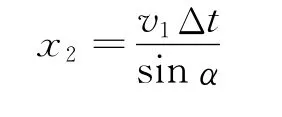
合位移
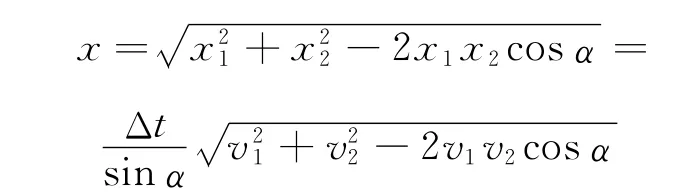
合速度
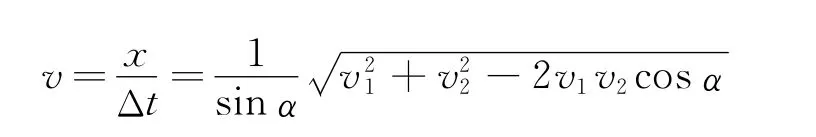
当两杆垂直时,α=90°,此时图16和图17一样,学生的解法才正确.
5 分运动具有独立性吗
有些教师在分析上述问题时使用了分运动的独立性原理,认为各分运动互相独立,互不影响.那么各分运动果真互相独立,互不影响?文献[4]给出了精彩回答:各分运动可以互相独立,也可以互相影响,不存在所谓的分运动的独立性原理.现将部分内容转述如下:
对于有空气阻力的抛体运动,当速度较小时,可以认为空气阻力大小与速度成正比,这时
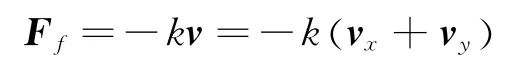
根据牛顿第二定律可得物体沿x和y方向运动的微分方程为
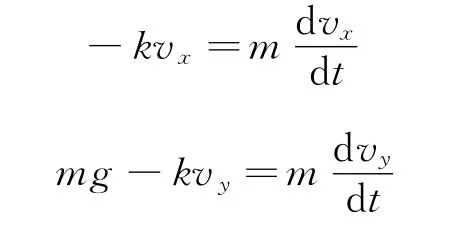
这两个方程表明,每个方程都不包含另一方向上的运动分量,可以分别独立地解出方程,此时两个分运动互相独立,互不影响.
再考虑速度较大,空气阻力大小是速度二次函数的情况.这时
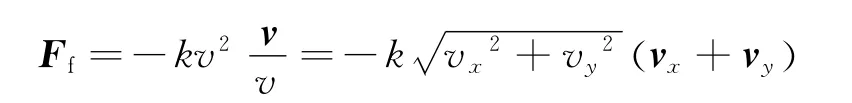
物体沿x和y方向运动的微分方程为
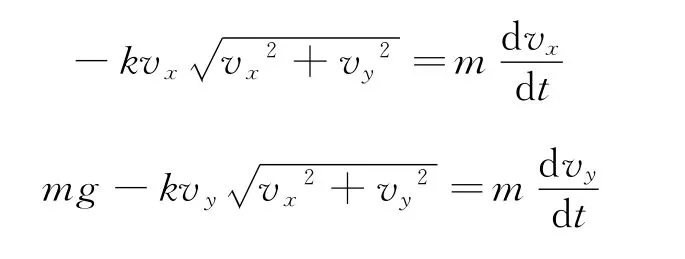
这两个方程表明,每个方程都包含了另一方向上的速度分量,明显反映出两个分运动彼此关联,并不是互相独立的.
由上述例子可以看出,各分运动可以互相独立,也可以互相影响,所谓的分运动的独立性原理自然就不正确了.
总之,物理模型在物理教学中固然重要,类比法也是解决问题的重要方法,但在处理具体问题时,不能单凭感觉,草率地与熟悉的模型进行类比,从而得到错误的结论.在进行运动的合成与分解时,每一个运动都要慎重分析,各分运动有时并非相互独立,互不影响,教会学生用联系的观点处理问题,具体问题具体分析,严防被直觉所误导.
1 李庆国,帅厚梅.物体的速度究竟是多少? 物理教师,2013(8):23~24
2 殷正徐.《物体的速度究竟是多少》究竟为什么?物理教师,2014(5):93~94
3 章建光.补议《两个博尔特拉着你能跑出5秒的百米成绩吗》.中学物理教学参考,2013(3):40~42
4 人民教育出版社.高中物理必修2教师教学用书.北京:人民教育出版社,2010.28~35

