对2015年高考江苏物理试题最后一题的研讨

杨 俊

（江苏省镇江中学 江苏 镇江 212017）

【试题再现】一台质谱仪的工作原理如图1所示，电荷量均为＋q，质量不同的离子飘入电压为U0的加速电场，其初速度几乎为零.这些离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场，最后打在底片上.已知放置底片的区域MN＝L，且OM＝L.某次测量发现MN中左侧区域MQ损坏，检测不到离子，但右侧区域QN仍能正常检测到离子.在适当调节加速电压后，原本打在MQ的离子即可在QN检测到.

（1）求原本打在MN中点P的离子质量m；

（2）为使原本打在P的离子能打在QN区域，求加速电压U的调节范围；

（3）为了能够在QN区域将原本打在MQ区域的所有离子检测完整，求需要调节U的最少次数.（取lg2＝0.301，lg3＝0.477，lg5＝0.699）

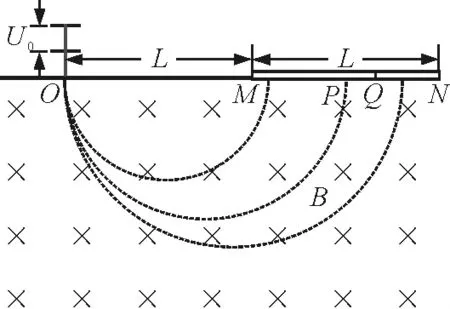
图1

试题立意：本题旨在考查考生对带电粒子在匀强电场和匀强磁场中的运动性质及基本规律的掌握，考查学生将物理情景进行数学建模并运用数学解决物理问题的能力.本题属于难题.

本题以质谱仪为背景，考查学生解决组合场问题的方法.本题（1）、（2）两小问比较容易，属于通则通法的考查，通过运用带电粒子在匀强电场中加速运动后的速度与粒子在匀强磁场中做圆周运动的半径之间的关系推演出加速电压U与粒子的质量m及几何半径之间r的关系式.第（3）问难度较大，属于物理中的动态问题，考生必须理解物理情景，找出第一、二次调节电压后同一粒子在两种情形下的电压和半径之间的关系式，根据两次调节电压后的表达式的相似性，再运用数学归纳法推出通式，加上边界条件得解.第（3）问既需要学生有较强的物理思维应变能力，同时对考生的数学建模能力提出较高要求.数列思想和数学归纳法本身就是高中数学应用的难点，现还要求考生运用其构建并处理物理问题，对考生的综合能力提出挑战.

多思路解题：对第（3）问的研究.

思路1：采用“分段逼近法”

解法1：从底片MQ右端向QN段分次逼近，如图2所示.

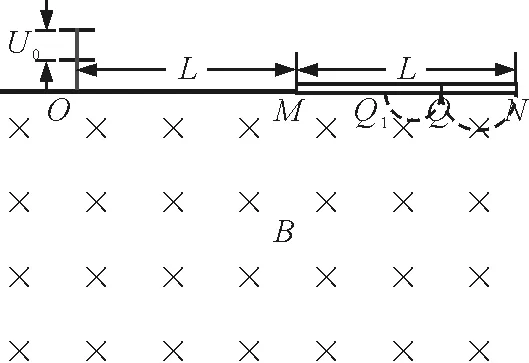
图2

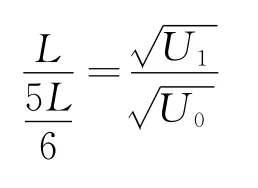
此时，原本半径为r1打在Q1的离子打在了Q点，则

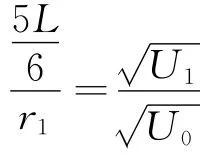
解得

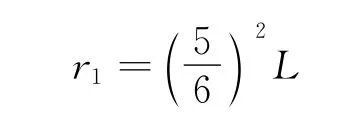
第2次调节电压到U2，使原本打在Q1的离子打在N点，原本半径为r2打在Q2的离子打在了Q1上，则

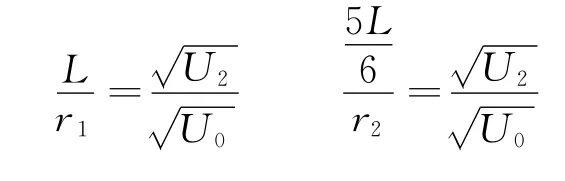
解得

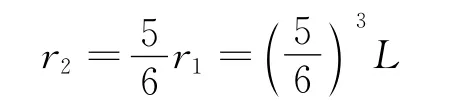
同理可得，第n次调节电压，有

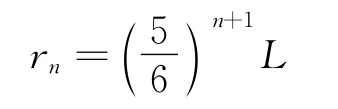
为保证检测完整，有

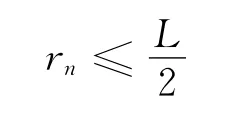
解得

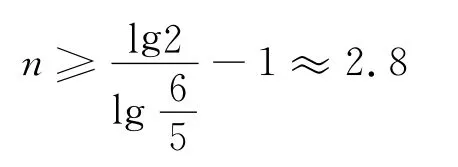
即最少调压3次.

解法2：从底片MQ左端向QN段分次逼近，如图3所示.

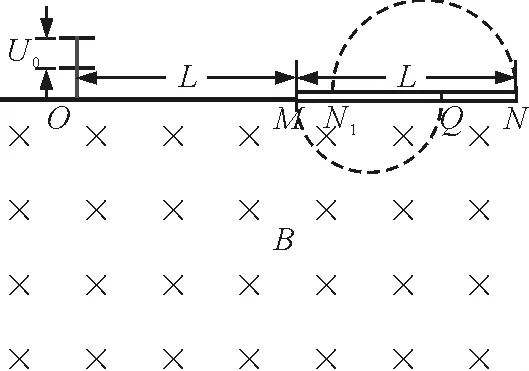
图3

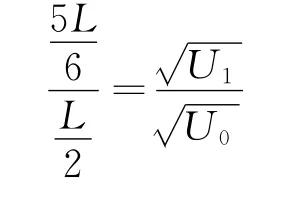
此时，原本半径为r′1打在N1的离子打在了N点，则

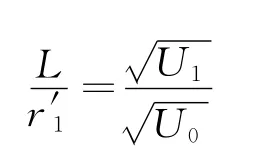
解得

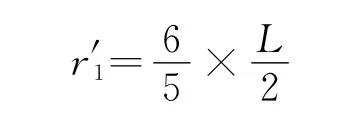
第2次调节电压到U2，使原本打在N1的离子打在Q点，原本半径为r′2打在N2的离子打在了N点，则

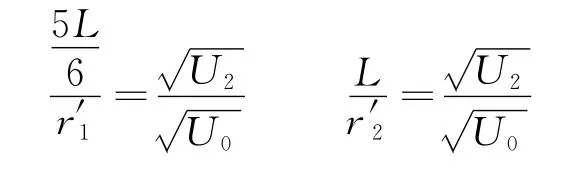
解得

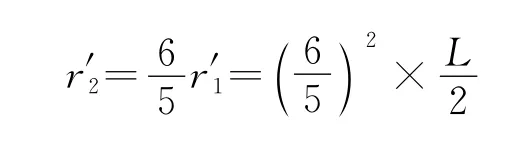
同理可得，第n次调节电压，有

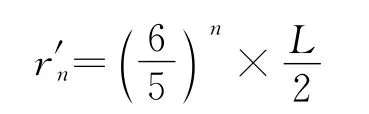
为保证检测完整，有

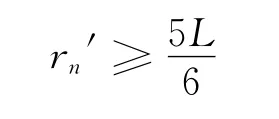
同样解得n≥2.8，即最少调压3次.

思路2：利用“定质（量）比”即为“半径比”调整

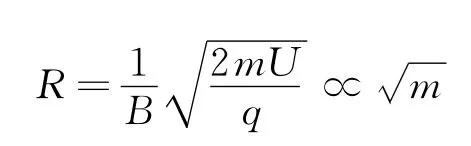
假设原本打在M，Q，N处离子的质量分别为m1，m2，m3，则

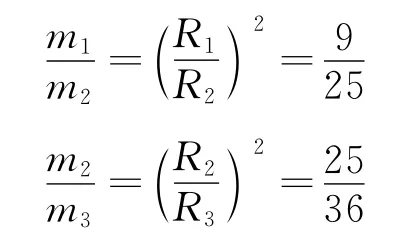
第1次调节电压，使质量为m1的离子打在Q点，质量为mx的离子打在N点则

第2次调节电压，使质量为mx的离子打在Q点，质量为my的离子打在N点则

第n次调节电压，使质量为mt的离子打在Q点，质量为mn的离子打在N点则

为保证检测完整，有mn≥m2，即式（1）×式（2）×……×式（n）得

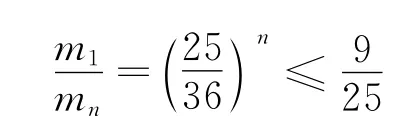
同样解得n≥2.8，即最少调压3次.

思路3：采用“累加求和法”（分次叠加求覆盖长度）

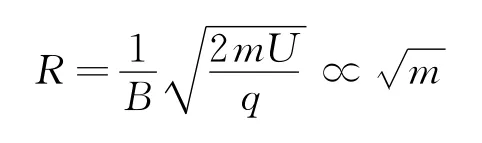
第1次调节电压，使原本打在M的离子打在Q点，原本打在N1的离子打在N点.

令MN1＝l1，由等比分比性质知

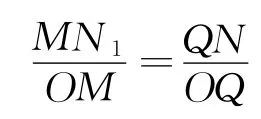
即

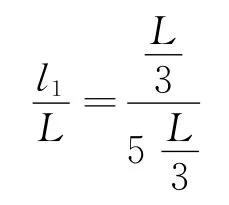
则

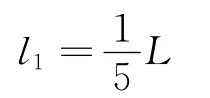
第2次调节电压，使原本打在N1的离子打在Q点，原本打在N2的离子打在N点.

令N1N2＝l2，同样由等比分比性质知

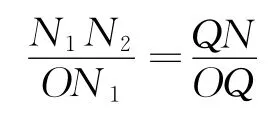
即

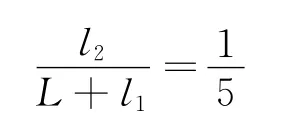
则

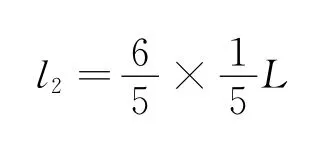
同理可得，第n次调节电压

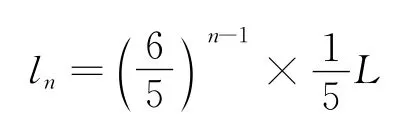
将各分段“累加求和”，为保证检测完整须满足

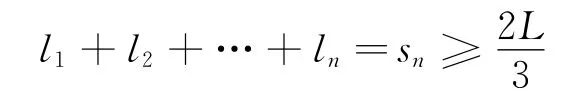
即

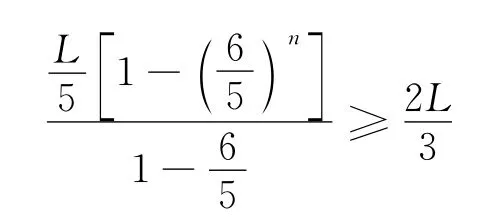
同样解得n≥2.8，即最少调压3次.

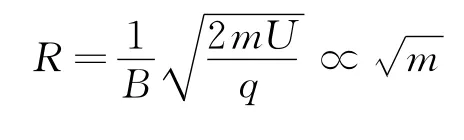
第1次调节电压，使原本打在Q的离子打在N点，原本打在Q1的离子打在Q点.

令Q1Q＝l′1，由等比分比性质知

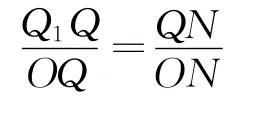
即

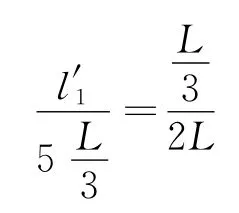
则

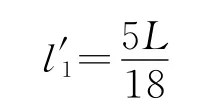
第2次调节电压，使原本打在Q1的离子打在N点，原本打在Q2的离子打在Q1点.

令Q2Q1＝l′2，同样由等比分比性质知

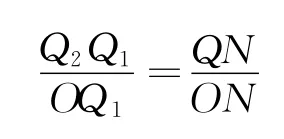
即

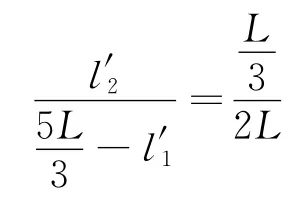
则

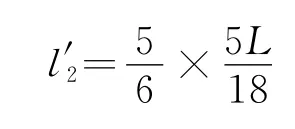
同理可得，第n次调节电压

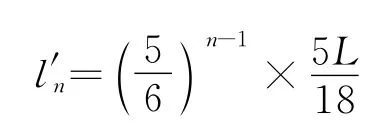
将各分段“累加求和”，为保证检测完整须满足

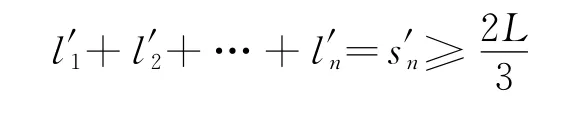
同样解得n≥2.8，即最少调压3次.

本文对2015年高考江苏物理试卷最后一题（民间常称之为压轴题）做了研讨，该题以质谱仪为背景，意在考查考生对带电粒子在匀强电场和匀强磁场的运动性质及基本规律的掌握，考查对物理思想的应变能力，将物理情景进行数学建模能力，运用数学知识解决物理问题的能力等.

笔者用多思路多解法对该题做了求解处理，试图从多角度多侧面启发和引导学生夯实基础知识，提高综合能力，成为合格的人才.