In 和Cu 掺杂对Sn 基钎料抗电性能影响的第一性原理研究

黄彬彬，张星辉

(1. 福建师范大学闽南科技学院，泉州362332;2. 西南交通大学现代物理研究所，成都610031)

1 引 言

随着电子设备的微型化和集成电路的高度密集，电迁移(EM)已成为破坏集成电路可靠性的一个不可逆因素. 在过去的几年中，特别是对倒装芯片Sn 基钎料凸点接头的电迁移(EM)失效进行了广泛的研究［1-2］. 目前，最有前途的Sn 基钎料主要有SnPb、SnCu、SnAg、SnIn 和SnInCu 等几种合金，并且其焊点的电迁移机制得到了国内外学者广泛的研究［3-4］. 研究发现对于含Sn 和Pb两种元素的SnPb 共溶合金在电迁移过程中的主导原子是由温度决定的［4］. 但是对于SnCu、SnIn-Cu、SnAgCu 等共溶合金(为了简化，命名为SnTM)而言，其电迁移的过程中主要的迁移原子为Cu 原子. 此外，SnTM 相对于SnPb 具有更长的电迁移寿［6］. Liu 等［5］人研究发现添加微量的Cu 可以提高SnPb 合金的电迁移性能. Yamanaka等［6］人指出添加微量的In 可以提高Sn 基钎料的抗电性能，并且其电迁移过程In 原子为主要的迁移原子. 但是，到目前为止，Cu 原子或者In 原子在Sn 基钎料中为什么是主导的电迁移原子的机制还尚未完全清楚. 而且，对于Cu 和In 等元素的添加为什么能够提高Sn 基钎料的抗电性能也需要进一步研究.

一般来说，电迁移产生的原子通量J 可以这样描述［7］:

其中C 代表着迁移原子的溶度，D 代表着扩散率，其表达式为D =D0exp(-Q/kT)，这里的D0为振动频率，Q 为扩散激活能，k 为波尔兹曼常数，T为绝对温度. F 代表着电迁移的驱动力，其可表示为F=Z*eE，这里e 为电子的电荷，Z*为有效电荷数，E 为电场强度. 通过方程(1)可知，Cu和In 一定是通过影响Sn 基钎料的有效电荷数Z*或者扩散激活能Q 来提高Sn 基钎料的抗电性能.

Dysonet 等 人［8-9］通 过 实 验 室 的 方 法 对 于SnTM(TM=Cu 和Au)体系的间隙扩散机制进行了研究，结果表明，Cu 和Au 在β 相的Sn 基钎料中沿C 轴的扩散速率快于沿a 轴的扩散速率. 众所周知，电迁移是一个定向的质量流传输过程，原子受到电子风力作用后，会在阳极聚集，而在阴极会产生空洞，这意味着在贵金属的扩散通道里分布着许多空位或者缺陷，因此，空位介质扩散在电迁移机制中也是一种非常重要的扩散机制.

所以，为了简化，本文的电迁移机制只考虑空位介质扩散机制，通过密度泛函理论对Cu 或者In 置放Sn 基钎料中部分Sn 原子对Sn 基钎料扩散激活能影响进行研究. 此外，还分析了掺杂的溶质原子对体系的稳定性和电子结构的影响.

2 计算方法

计算采用基于广义梯度近似(GGA)的密度泛函理论，选用PBE 泛函描述电子关联能［10］. 从第一性原理出发，将晶体的多电子方程转化为Kohn-Sham 方 程，选 择 超 软 赝 势［11］(Ultrasoft Pseudopotentials)描述电子和离子的相互作用. 用CASTEP 模块［12］进行结构优化和电子总能计算，平面波截止能取为330eV，简约布里渊区采用Monkhors-Pack 方法［13］取适量K 点，其K 点取为2 ×2 ×4. 一般来说，Cu 在Sn -Cu 共晶软钎料中的溶度大约为0.7wt%，而In 在Sn-In 或Sn -In-Cu 钎料中的溶度大约为6wt%. 因此，SnTM 可以被认为稀释固溶体. 相似的方法在Yu 等［14］人的研究中也可看到. 我们构造了一个2 ×2 ×2 的Sn32超胞(见图1)，再分别用一个Cu 或In 替代Sn32中的一个Sn，Sn32和Sn31TM(=Cu、In)在计算过程中，保证其晶格常数充分弛豫，并保证其能量变化小于1 ×10-6ev. 为了计算的选定条件具有可比较性，替代位置都选取在Sn32超胞中心处(见图1)，在结构优化时，保证各体系的超胞充分弛豫，其计算结果收敛为:总能变化小于1.0 ×10-5eV·atom-1，原子受力小于0.3 eV·nm-1，公差偏移小于0.01 nm，应力偏差小于0.05GPa，自洽精度为1.0 ×10-6eV·atom-1. 最后采用过渡态搜索的(NEB)方法获得原子的迁移能，此方法经常用来寻找原子迁移的能量最低的反应路径.

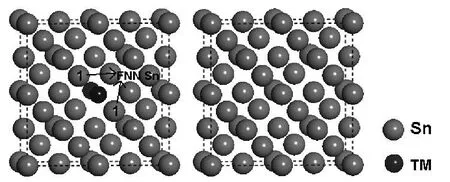
图1 Sn32和Sn31TM (TM = Cu，In)的超胞模型. “1”代表着和TM 原子最近的Sn 原子Fig.1 The super cell models of Sn32 and Sn31 TM (TM =Cu，In). The "1" represents the first nearest neighbor(FNN)Sn by dopant atoms

3 结果和讨论

3.1 晶体结构及优化结果

目前，商业上所用的Sn 基钎料的晶体结构为β -Sn［15］，其空间群为141/AMD，晶胞参数为a=b=5.831Å，c =3.182Å，α =β =γ =90°，其中Sn 原子的占位为4a (0，0，0). 由β -Sn 构建的Sn31TM (TM= Sn，In，Cu)超胞模型优化结果见表1. 从表1 可知，优化后，Sn32的a、b 和c 轴相对实验值分别增长了3.4%、3.4% 和1.4%. 其体积也相应变化到1169.90 Å3. Cu 和In 替代了Sn32的部分Sn 原子后，Sn32的晶体结构出现了明显变化，Sn31In 和Sn31Cu 的a、b 和c 轴相对Sn32出现一定的收缩，体积也相应的变化为1155.69 Å3和1101.25 Å3. Sn31TM (TM=In，Cu)超胞参数出现收缩，主要有以下两方面原因:一方面，由于Sn 的原子半径大于In 和Cu 原子，根据小原子替代大原子，其体积会出现一定收缩. 另一方面，由于Sn 、In 和Cu 原子外层电子排布不同，会引起TM (TM= Sn，In，Cu)原子和邻近的Sn 原子之间相互作用不同，从表1 的计算结果可以看出，In 和Cu 原子替代，应该是增强了其和邻近Sn 原子的相互作用. 具体的情况将在后面的3.3 节中进一步讨论.

表1 Sn31TM (TM= Sn，In ，Cu)的超胞参数Table 1 The supercell parameters of Sn31TM (TM= Sn，In，Cu)

3.2 抗电性能

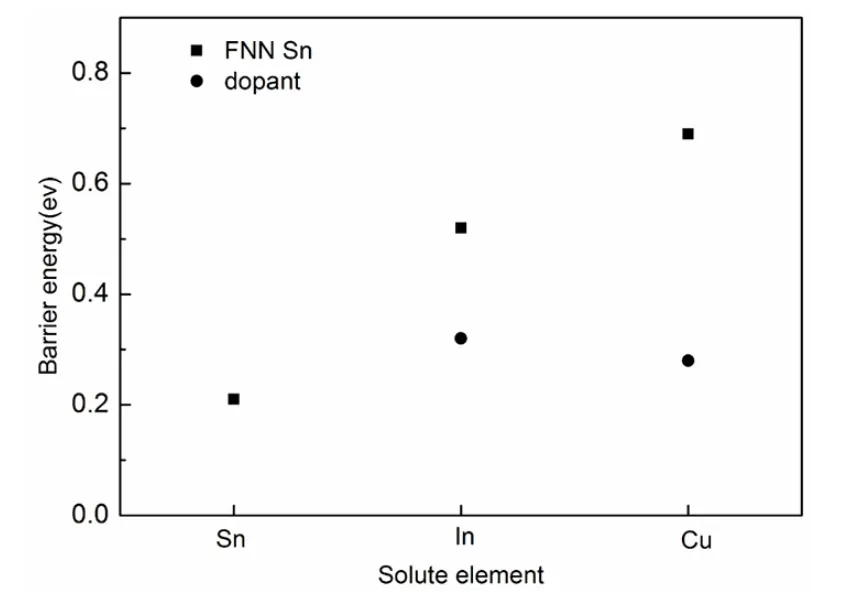
图2 掺杂原子和其最近的(FNN)Sn 原子的能量势垒Fig.2 Barrier energies of the solute atoms and their nearest neighbor Sn atoms. The square and roundness represent the energies of solute and FNN Sn atoms，respectively

为了理解Cu 和In 为什么能够提高Sn 基钎料的抗电性能，根据公式(1)可知，Sn31TM(=Sn、Cu、In)的抗电性能可以通过计算原子的扩散激活能Q 来表征，因此这里对Sn31TM(= Sn、Cu、In)的扩散激活能Q 进行计算，对于空位介质扩散而言，其扩散激活能Q 可以表示为:

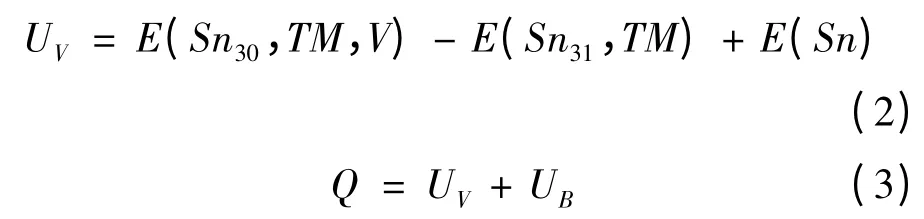
其中这里的Uv代表体系的空位形成能，E(Sn30，TM，V)表示含有一个溶质—空位对的体系总能量，E(Sn31，TM)表示含有一个溶质原子的体系总能量，E(Sn)代表着一个Sn 原子的能量. UB代表着原子的迁移能，其大小为体系过渡态总能和稳态总能之差. 通过NEB 方法获得原子的迁移能UB吐图2 所示，Sn 原子在Sn32的扩散迁移能垒为0.22eV，但掺杂了Cu 或者In 原子后其最邻近(FNN)Sn 原子(具体位置见图1)的自扩散能量势垒分别提高到了0.66 eV 和0.45 eV，这说明了Cu 或者In 原子的替代会阻碍FNN Sn 原子的迁移. 同时还发现Cu 或者In 原子在Sn31TM 的扩散迁移能势垒小于Sn 原子在Sn32的扩散能量势垒，这意味着Cu 或者In 原子在Sn31TM 体系中优先迁移. Tu 等［16］人对Cu/Sn 扩散偶的实验研究指出Cu 原子在Cu/Sn 界面反应过程中占主导地位，这和我们的计算结果相一致. 此外，我们发现在Sn31TM 体系中，Cu 或者In 原子和第二近的Sn 原子的自扩散能量势垒远小于FNN Sn 原子能量，这说明了Cu 或者In 原子和FNN Sn 原子存在着很强结合力，但是随着Cu 或者In 原子和Sn 原子距离的增大，其结合力就会减弱. 这个计算结果也和Dekker 等［17］人计算结果相一致. 另外，由公式(2)计算可知，Sn32的空位形成能为0.92eV，Sn31Cu 和Sn31In 的空位形成能分别为1.21eV 和1.18 eV，把以上这些计算结果代入公式(3)，可以得到Sn 在Sn32的扩散激活能Q 为1.14eV，其计算结果略高于实验结果1.04eV［18］. 而掺杂原子在Sn31Cu 和Sn31In 的扩散激活能Q 分别为1.49eV 和1.52eV. 其Cu 原子在Sn31Cu 的扩散激活能Q 也和实验结果1.44eV［19］较接近. 关于计算值和实验结果存在一定偏差的原因，主要和我们计算过程中所选取的计算精度和计算温(T =0 K)有关. 由于Cu 和In 掺杂后，Sn 基钎料具有更高的扩散激活能，因此Cu 和In 的掺杂相对于纯Sn 基钎料具有更好的抗电性能.

3.3 电子结构分析

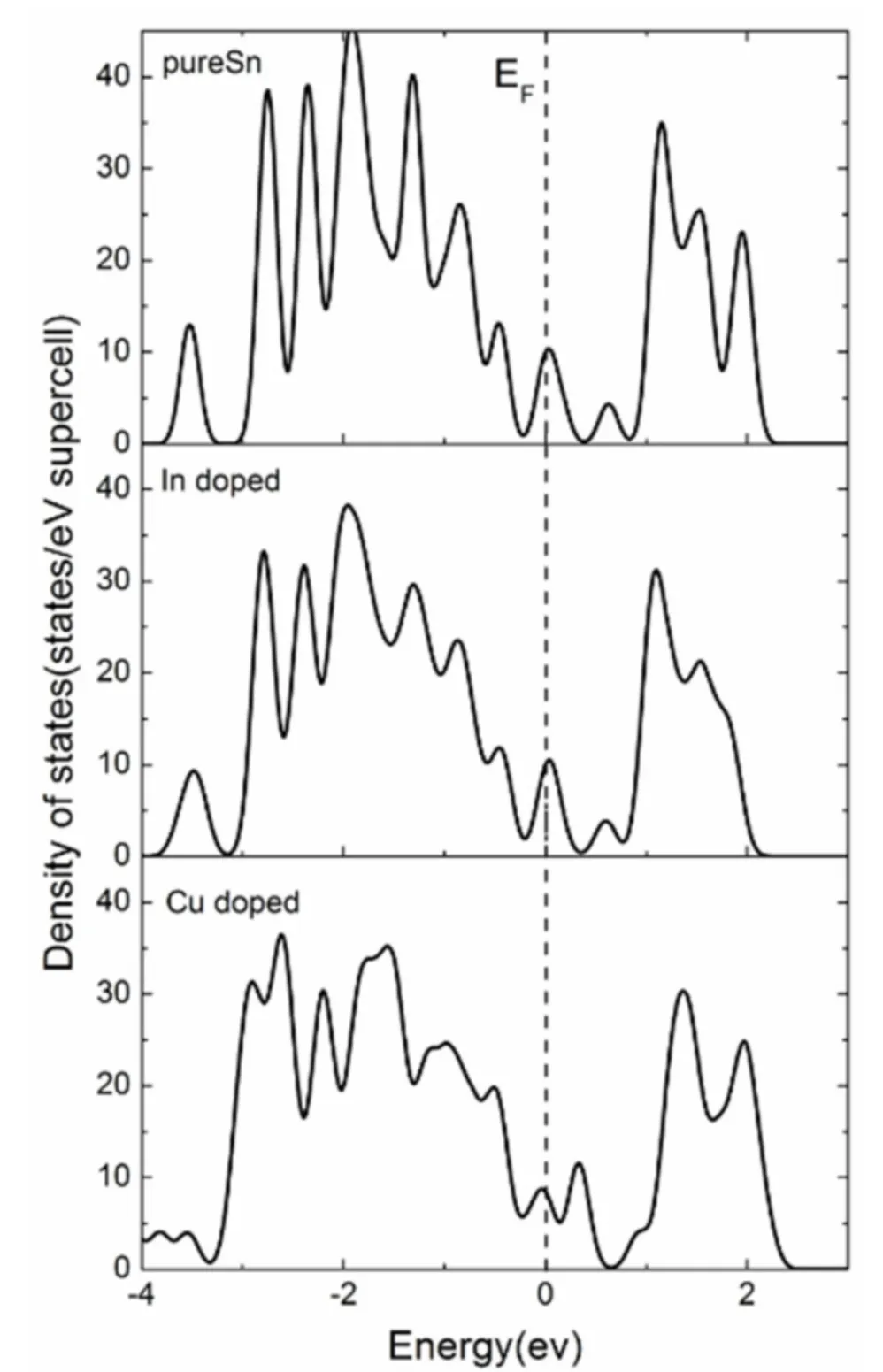
图3 Sn31TM(TM= Sn，In 和Cu)的总态密度图Fig.3 Density of states of Sn31 TM(TM = Sn，In and Cu，respectively)

为了进一步理解Cu 或In 掺杂前后Sn 基钎料的稳定机制，分别对Sn31TM(TM= Sn，In 和Cu)的总态密度图(TDOS)进行计算，结果如图3 所示，EF代表费米能级，由于TDOS 穿过EF，说明三种体系是金属. 对于TDOS 而言，费米能级处的电子态密度变化对体系的稳定性有着重要的影响，比较各图可知，在费米能级处都有一个小尖峰，没掺杂前小尖峰的峰值为10.04 states/eV，但是In 和Cu 加入后其峰值出现了相应的变化，分别变为9.65 和8.59 states/eV，由于峰值的减低，说明掺杂后费米能级处的电子出现转移，从图中可以看出，掺杂后TDOS 导带处分布着更多的电子，由于键合电子的增多，掺杂后体系相互间原子的作用力更强，体系就更稳定. 关于费米能级处峰值的减低会使体系更稳定在文献［13，20，21］中也有相应报道.

由于体系的成键强弱也是判断体系稳定性和原子迁移能力的一个重要指标，因此我们对各体系的电荷等密度图进行计算，因为电荷等密度图可以直观地看出电子云的重叠情况和判断原子间相互作用的强弱. Sn31TM(TM= Sn，In 和Cu)的电荷等密度图如图4 所示，从图中可以看出，在掺杂前，体系中各Sn 原子之间的电荷是均匀分布的(见图4a)，但是掺杂以后，体系中和掺杂原子邻近的Sn 原子的电荷转移出现明显的变化(见图4b 和4c)，表现出很强的相互作用(其中Cu -Sn键的相互作用最明显)，同时还可以观察到离掺杂原子较远的Sn 原子变化不明显，这说明了掺杂原子对较近的Sn 原子有着明显的影响，但离掺杂位置较远的原子影响很小，这和Dekker［17］指出的情况一致. 通过以上分析可知，Cu 或In 加入会使体系更稳定，并且会对邻近的Sn 原子产生较强的相互作用，因此，可以预见，在相同的电子风力的作用下(即相同的电场作用下)，在掺杂原子周围的Sn 原子就更难迁移，这样就提高了Sn 基钎料的抗电性能，这和前面扩散激活能的计算结果所反映的情况相一致.

图4 Sn31 TM(TM = Sn，In 和Cu)的电荷等密度图Fig.4 Contour maps of electron density of Sn31TM(TM = Sn，In and Cu，respectively)

4 结 论

本文采用第一性原理的方法对Sn31TM(TM =Sn，Cu 和In)的原子迁移能、扩散激活能和电子结构进行计算，计算结果表明，Cu 和In 的掺杂有利于提高Sn 基钎料的扩散激活能，体现出了更优良的抗电性能，并且Cu 的效果最明显. 而且我们还发现Cu 和In 的扩散迁移能小于FNN Sn 原子，所以Cu 和In 在掺杂的Sn 基钎料中是优先扩散的元素. 另外，以上的这些计算结果在电子结构分析中也得到了很好的验证，并且和实验观察到的现象也相一致.

［1］ Liu C Y，Ke L，Chuang Y C，et al. Study of electromigration - induced Cu consumption in the flip -chip Sn/Cu solder bumps［J］. J. Appl. Phys.，2006，100:083702.

［2］ Xu L，Pang J H L，Tu K N. Effect of electromigration- induced back stress gradient on nanoindentation marker movement in SnAgCu solder joints［J］. Appl.Phys. Lett.，2006，89(22):221909.

［3］ Xu L，Han J K，Liang J J，et al. Electromigration induced high fraction of compound formation in SnAgCu flip chip solder joints with copper column［J］. Appl.Phys. Lett.，2008，92(26):262104.

［4］ Lee T Y，Tu K N，Frear D R. Electromigration of eutectic SnPb and SnAg3.8Cu0.7flip chip solder bumps and under-bump metallization［J］. J. Appl. Phys.，2001，90(9):4502.

［5］ Liu C Y，Chih C，Liao C N，et al. Microstructure -electromigration correlation in a thin strips of eutectic SnPb solder stressed between Cu electrodes［J］. Appl.Phys. Lett.，1999，75(1):58.

［6］ Yamanaka K，Tsukada Y，Suganuma K. Solder electromigration in Cu/In/Cu flip chip joint system［J］. J.Alloy. Compd.，2007，437(1):186.

［7］ Huntington H B，Grone A R. Current-induced marker motion in gold wires［J］. J. Phys. Chem. Solids，1961，20(1):76.

［8］ Dyson B F，Anthony T R，Turnbull D. Interstitial diffusion of copper in tin［J］. J. Appl. Phys.，2004，38(8):3408.

［9］ Dyson B F. Diffusion of gold and silver in tin single crystals［J］.J. Appl. Phys.，2004，37(6):2375.

［10］ Marlo M，Milman V. Density - functional study of bulk and surface properties of titanium nitride using different exchange - correlation functional ［J］.Phys.Rev. B，2000，62(4):2899.

［11］ Vanderbilt D. Soft self - consistent pseudo potentials in a generalized eigenvalue formalism［J］. Phys. Rev.B，1990，41(11):7892.

［12］ Segall M D，Lindan P J D，Probert M J，et al. Firstprinciples simulation:ideas，illustrations and the CASTEP code［J］. J. Phys.:Condens. Matter.，2002，14(11):2717.

［13］ Monkhorst H J，Pack J D. Special points for Brillouin-zone integrations［J］. Phys. Rev. B，1976，13(12):5188.

［14］ Yu C，Ji J X，Yang Y，et al. First principles calculation of the effects of solute atom on electromigration resistance of Al interconnects［J］. J. Phys. D:Appl.Phys.，2009，42(12):125501.

［15］ Wołcyrz M，Kubiak R，Maciejewski S. X-ray investigation of thermal expansion and atomic thermal vibrations of tin，indium，and their alloys［J］. Phys. Status Solidi，1981，107(1):245.

［16］ Tu K N，Thompson R D. Kinetics of interfacial reaction in bimetallic Cu/Sn thin films［J］. Acta Metall.，1982，30(5):947.

［17］ Dekker J P，Gumbsch P，Arzt E，et al. Calculation of the electromigration wind force in Al alloys［J］. Phys.Rev. B，1999，59(11):7451.

［18］ Huang F H，Huntington H B. Diffusion of Sb 124，Cd 109，Sn 113，and Zn 65 in tin［J］. Phys. Rev. B，1974，9(4):1479.

［19］ Chao B，Chao S H，Zhang X，et al. Investigation of diffusion and electromigration parameters for Cu – Sn intermetallic compounds in Pb-free solders using simulated annealing［J］. Acta Mater.，2007，55(8):2805.

［20］ Xu J H，Oguchi T，Freeman A J. Solid - solution strengthening:Substitution of V in Ni3Al and structural stability of Ni3(Al，V)［J］. Phys. Rev. B，1987，36(8):4186.

［21］ Hong T，Watson-Yang T J，Guo X Q，et al. Crystal structure，phase stability，and electronic structure of Ti-Al intermetallics:Ti3Al［J］. Phys. Rev. B，1991，43(3):1940.