二维阵列超视距雷达的选频方法

罗忠涛何子述卢 琨陈绪元

①(电子科技大学电子工程学院 成都 611731)

②(南京电子技术研究所 南京 210013)

二维阵列超视距雷达的选频方法

罗忠涛*①何子述①卢 琨②陈绪元②

①(电子科技大学电子工程学院 成都 611731)

②(南京电子技术研究所 南京 210013)

该文提出一种通过预测到达任务区域路径信噪比，自适应地为天波超视距雷达选择工作频点的方法。利用2维阵列的俯仰维分辨能力，克服了传统方法无法从返回散射电离图中分离多模/多径信号的缺陷。雷达通过电离层探测设备和2维接收阵列，获取返回散射数据、环境干扰数据和电离层状态数据。然后利用电离层模型和状态数据，推算各频点对任务区域的照射路径。运用2维自适应波束形成抑制环境干扰噪声，并处理返回散射数据以预测各路径回波强度。最后计算各频点路径在脉冲压缩后的信噪比，选择信噪比最大值的频率为最优工作频点。

超视距雷达；频点选择；2维阵列

1 引言

天波超视距雷达(Over-The-Horizon Radar, OTHR)工作在高频段(6～28 MHz)，是一种有效的远程预警手段[1,2]。由于高频电磁波在电离层中的传播路径依赖于其频率，工作频点制约着OTHR性能，比如最大最小探测距离及回波强度。其次，高频段背景中分布着各种无线电干扰和噪声，包括各种短波通信电台[1,3]。因此，OTHR频点选择非常重要，既要求覆盖任务区域回波能量高，还需要尽量避开干扰所占频谱。

传统OTHR工作频点是人工选择，过程主要分两步[1,2]。第1步是依据返回散射“群时延距离-频率-幅度”电离图，描述扫频信号在经过电离层后被地面/海面后向散射返回接收站的能量强度。工作人员可根据任务位置对应的大致时延距离，确定幅度较强的频段。第2步，根据环境干扰频谱监测，选择频段内未受干扰或干扰尽量少、具有足够带宽的频点作为工作频点。随着OTHR技术的发展，选频方法也在革新。文献[3]考虑空域干扰的问题，提出自适应滤波后再比较各频点噪声能量大小。文献[4]制作距离对应频率-俯仰角表格作选频参考。不过传统线阵制约了OTHR选频技术的发展。由于线阵不能提供俯仰角的分辨力，无法分离多模和多径信号，因而无法针对任务位置精确选择真正具有最强回波的频点。

近年来2维阵列在OTHR中的使用研究得到了关注[5−9]。由于电离层中电波传播路径与俯仰角紧密联系，2维阵列所提供的俯仰角分辨力给OTHR带来了额外增益，比如杂波抑制[8]和工作模式选择[9]。2003年研制的法国雷达NOSTRADAMUS为单基体制[5]，发射和接收阵列为2维阵列，可提供多种功能的电离图，包括俯仰角和距离的3-D电离图，并配以先进而复杂的频率管理系统(Frequency Management System, FMS)理念。可惜的是，它并没有给出具体可行的雷达选频目标和操作方案。本文提出一种适合2维阵列OTHR的选频工作方案，关注任务区域路径的回波和噪声强度，选择信噪比最优的频率为工作频点。

2 OTHR选频特点和2维阵列

OTHR工作频点选取考虑的主要因素有两个：回波强度和噪声功率。为实时认识电离层状态，OTHR配备电离层探测设备，一般有返回散射探测设备，垂直探测设备和斜向探测设备等。其中返回散射处理对象是扫频信号被监测区域地/海面后向散射的回波，反应了散射回波经传播损耗的效果，提供各频点回波强度预期的重要指示信息。垂直和斜向探测设备主要是提供电离层状态信息，比如电离层高度、电子浓度等，通过描绘3维的电离层电子浓度图，辅助评估方位偏差和坐标变换系数等。此外，OTHR还配备环境监测设备，进行干扰频谱和环境噪声监测，以避开强干扰进行工作。

传统选频方法基于以上两个监测信息，有一个无法克服的缺陷：不能预估任务区域返回散射强度。在缺乏俯仰角分辨力的情况下，即使OTHR推算到照射任务区域的射线信息，也由于无法分离多模/多径信号，从而无法将返回散射数据的群时延距离-频率-幅度图转换为地面距离对应幅度。此外，传统方法由人工选取频点，主观性较强，不适应现代雷达要求自适应的发展趋势。

2维阵列的列装和使用是近年来OTHR的一个发展方向[6]，增加了俯仰维干扰的抑制能力[8]和雷达信号处理功能[9]。2维阵列的建设，可源于传统线阵的改造。本文研究的OTHR，其发射阵列依然为线阵，控制发射能量的方位角如图1所示。接收阵列由1维扩展为2维，每一维分别具有K1和K2个阵元，均匀分布间隔分别为d1和d2，入射方向由方位角ϕ和俯仰角θ确定。探测和监测设备的接收天线可与雷达目标检测阵列共享，不仅能节约设备研制和场地建设成本，也使所监测的环境最大限度地近似检测目标时的外部环境。本文介绍选频方法以图1中简单普遍的矩形网格的2维阵列为例，但选频方法并不限定2维阵列形式。

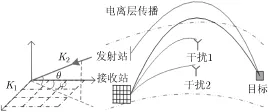
图1 2维阵列的OTHR工作场景示意图

3 2维阵列OTHR选频方法

3.1 方案和框图

与传统方法相同，2维阵列OTHR选频依赖于雷达探测和监测得到的有关电离层和环境的数据，按其来源分类有：(1)返回散射数据：返回散射探测设备发射机扫频高频段(6～28 MHz)，2维接收阵列接收地/海面返回的回波数据，包含有地/海面回波，环境干扰和噪声。(2)环境监测数据：电离层探测及雷达信号发射机关机(或者发射机与接收机工作在不同频段)，2维阵列录取环境干扰噪声数据。(3)电离层状态数据：基于实时采集的电离层探测数据，参考经验或模型(如国际参考电离层模型)，通过电离图反演法[10]或重构法[11]，得到在3维空间的电离层电子浓度Ne(cr)，其中cr=(ϕ,r,h)表示了电离层某点对应于雷达接收阵列的坐标，r表示地面距离，h表示与地心的距离，主要指电离区域高度段。

设任务区域为地/海面(忽略飞行目标高度)，对应接收阵列的方位角为ϕt，地面距离为rt。从雷达性能角度看，希望照射到任务区域的散射回波能量高，接收数据在波束形成、脉冲压缩和相干积累等处理后，信噪比达到最优。基于监测数据和选频目标，本文提出的OTHR选频方案的流程主要分5步，如图2所示。

3.2 第1步：常规粗选频段

图2 OTHR选频流程框图

粗选频段后，将其等分，以便从中细选出最佳频点。令最大频点为fmax，最小频点为fmin，划分间隔fΔ可视雷达设备和系统条件选取。待选频点f的可选空间为F=[fmin,fmin+fΔ,…,fmax−fΔ,fmax]。 OTHR根据扫频返回散射结果，按照常规雷达“保证子区覆盖、场强尽可能大、可用时间概率大”等原则[1]，来制定对感兴趣距离的适宜频段，一般范围在300～1000 kHz[3]。OTHR常用信号带宽为20～40 kHz(空中目标)和40～200 kHz(海面目标)。可设置粗选频点间隔为带宽一半或更小。由适宜频段范围和频点间隔，得到粗选频段的数目，然后给出待选频点f的可选空间F。

3.3 第2步：电离层射线追踪

利用射线追踪技术选频的关键在于电离层实时信息。电离层探测设备和电离图看起来种类多样，实际上均源于一个因素电子浓度在3维空间的分布。国内外已有相关算法，可根据实时探测数据估计电离层参数，进而推算电子浓度分布Ne(cr)[10−13]。基于电离层中电波传播3条定理，可计算电波照射地面距离时对应的等效传播距离(射线距离)和俯仰角度[1]。相关应用已见于目标高度测量[14,15]。本文中射线追踪的任务在于，根据电离层状态数据Ne(cr)，推算各频点可能照射在任务区域的射线情况。

本文采用MQP(Multi-Quasi-Parabolic)电离层模型来预测射线路径[14]。MQP模型将电离层进行分层，模型参数有层最大电子浓度(或临界频率)、层高和半厚度。为简化讨论，设电离层电子浓度Ne(h)在等海拔线上相同，与地面距离r无关。在MQP模型下，频率f的电波照射在地面距离rt的任务位置，其路径的俯仰角θt，射线距离Rt，与rt满足关系

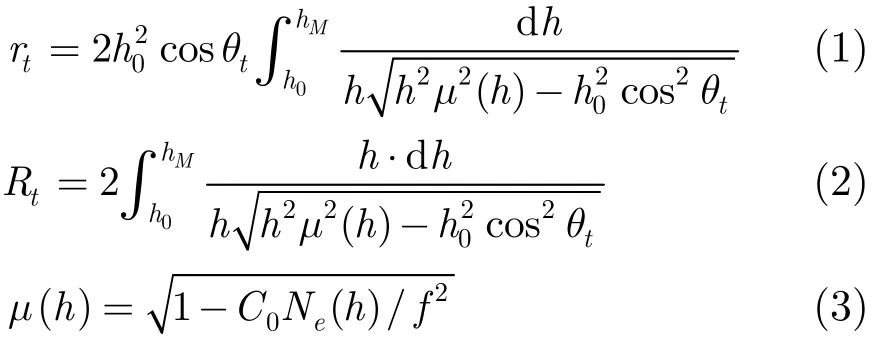
其中C0为常数，h0为地球半径，hM为等效反射高度。由式(1)～式(3)可以解算出各频点电波能否照射任务区域以及可行路径的参数。

对待选频点f推算其传播路径，设路径条数为Lf(下标表示与频点f有关的量，下同)。如果Lf＞1，表示发生了多径现象。频点f的第l条路径，l=1, 2,…,Lf，俯仰角和射线距离分别为θfl和Rfl。对于不同路径，方位角ϕt和地面距离rt不变。

3.4 第3步：自适应波束形成

考虑高频段外界干扰及其抑制问题，为抑制方向性的射频干扰，可将自适应数字波束形成(Adaptive Digital Beam Forming, ADBF)纳入雷达信号处理，因而要求选频方法给出与之相配的最佳频点。为避免过强的地海杂波，ADBF所需的训练快拍样本是一段纯环境干扰数据，且可采用宽带接收。

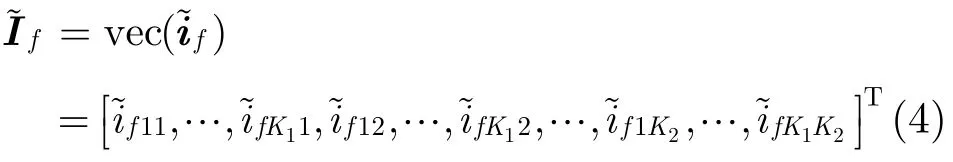
其中(·)T表示转置。注意fk1k2为时间上的采样序列，k1k2表示接收阵元序号。估计的干扰空间协方差矩阵为

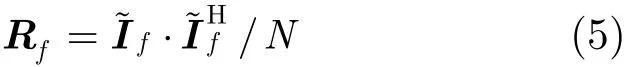
其中N为采样点数，(·)H表示共轭转置。对于频点f第l条路径，使用MVDR方法，ADBF最优权向量为

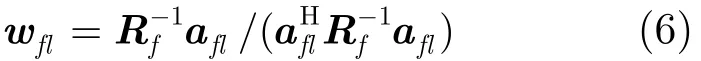
其中afl为2维阵列的接收导向矩阵Afl的列向量形式。导向矩阵Afl维数为K1×K2，第k1行k2列元素为

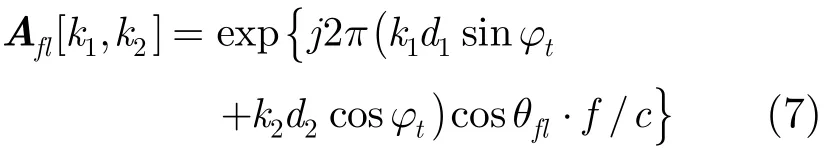
其中c表示光速。ADBF后的干扰数据为

其功率谱密度为Zfl(ω)。

对每个频点的每条路径进行单独ADBF是最优的选择，ADBF总次数决定于待选频点f数量及多径条数Lf。在通常情况下，相近频点对任务区域的电离层同层路径变化很小。如果作简化处理减少运算量的考虑，可在同电离层反射路径使用相同权向量，即将未经带通滤波的数据代替式(4)～式(8)中。此外，ADBF可能由于阵元较多造成运算量过大。可采用一些降低计算量和复杂度的方法，比如降秩处理[16]。

3.5 第4步：预测回波强度

在第1步中通过单行阵元的返回散射数据处理所得“群时延-频率-幅度”特性图，是不同俯仰角路径能量的叠加结果，无法读取某俯仰角或地面距离对应的回波强度。这正是传统选频方法的无奈之处。在2维阵列提供俯仰维波束形成后，对返回散射数据的处理可得到与俯仰角相关的散射强度分布，从而预测各频点路径的回波强度。具体做法是：

注意两点。第一点是ADBF对象，加权向量wfl产生于训练数据(纯环境干扰)，而后用于返回散射数据(包括干扰、杂波和可能的目标回波)。第二，这里预测的回波强度是射线追踪中电波传播路径推算的补充和增强。射线追踪技术推算频点电波到达任务区域的可行性仅是理论上的推断，没有考虑电波损耗等因素。而某些理论上存在的路径可能实际上会由于电离层遮挡或路径损耗的原因而变弱。比如，理论上电波可以通过E和F1两层传播，但实际上E层吸收能力很强，导致没有或极弱电波到达F1层。通过2维处理预测回波强度，便可评估这种现象。

多径的回波强度会在2维处理的返回散射强度图上得到体现。对于射线追踪技术推算的频点f第l条路径，在其俯仰角θfl返回散射“群时延-幅度”特性图中，必能找到射线距离Rfl对应的幅度，即为预测的回波强度Pfl。注意，这里回波强度是相对值而非绝对值，是一种对传播和接收损耗等的预期，没有将海况散射强度或目标RCS变化(比如随照射角)影响考虑在内，或者说认为它们在待选频段内是相同或相近的。

3.6 第5步：预测SNR选最佳

之前考虑了回波强度因频点和路径的不同而不同，另一方面干扰噪声功率也随频率变化。不同于传统方法中手动选择“干净”或“干扰尽量小”的频点，本文方法从理论上计算各路径在波束形成，脉冲压缩和多周期相干积累等信号处理后的信噪比，作为选频依据。干扰功率谱密度Zfl(ω)和预测回波强度Pfl均为波束形成后的数据，考虑相干积累在各频点的增益一致，下面分析脉冲压缩的影响。

设发射信号频谱为Sf(ω)，接收机脉冲压缩的滤波器响应为hf(t)，傅里叶变换为Hf(ω)。根据滤波器理论，那么频点f第l条路径信号在脉冲压缩后预测信噪比为

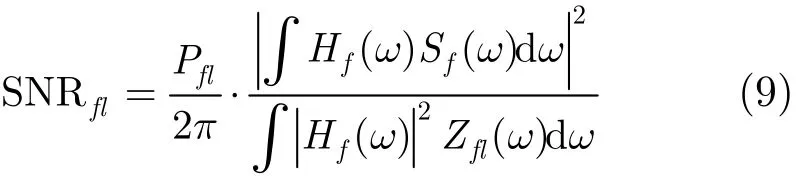
对所有频点路径，将Zfl(ω)和Pfl代入式(10)预测信噪比，然后选取最优信噪比对应的频点。多径传播会使该工作复杂化，因为它属于非相干处理，其联合的综合效果与各路径信噪比的数值关系较为复杂。这里采用简单处理，取各路径最大信噪比为准。最终选取的工作频点为

有时人们还关心覆盖率问题，希望了解频点对于除任务区域外其他距离的照射和返回散射情况。因此，可从第2步开始，对感兴趣的俯仰角范围估计返回强度和信噪比。返回散射强度图以俯仰角为变量，作出单频点“群时延-俯仰角-幅度”特性图。此图为人们所熟悉，可由具备扫描俯仰角天线的探测设备测得[17]。

3.7 流程总结

2维阵列OTHR为任务区域选择最佳频点的操作流程归纳为：

(1)返回散射探测设备发射扫频信号，2维阵列接收回波信号，获得返回散射数据，选取单行数据进行方位角的常规接收波束形成，处理得到“群时延-频率-幅度”图，根据任务区域地面距离对应的大致射线距离/群时延，选取图中返回能量较强的频段作为粗选频段(与传统方法相似)，确定待选频点f的范围；

(2)根据实时探测和经验、重构或反演法等方法，得到电离层实时状态电子浓度分布Ne(cr)，利用射线追踪技术，预测粗选频段内各频点照射任务区域的可行路径参数，包括俯仰角θfl和射线距离Rfl；

(4)采用权向量wfl对返回散射数据进行2维波束形成，处理得到频点f在俯仰角θfl的“群时延-幅度”关系，读取射线距离Rfl对应幅度Pfl；

(5)考虑发射信号频谱和脉冲压缩，将Pfl和Zfl(ω)代入式(9)或式(10)得到各路径的预测信噪比，选最优值对应频率为最佳工作频点。

OTHR雷达根据全频扫描返回散射数据，确定粗选频段后，可对粗选频段重点扫描，提高数据更新频率。粗选频段范围约为1 MHz，纯环境干扰数据在1 s内录取完成，可选在发射机关机或雷达换波位频段的时段。电离层实时参数由电离层探测设备持续更新。取得所需数据后，后台进行选频运算，采用高性能计算机可控制运算时间在1 s内，最后将所选工作频点传至发射站。整个录取数据和频点选取总计工作时间约2 s。选频工作应纳入雷达资源管理系统，选频更新频率可视环境和任务情况(海面目标积累时间约30～60 s，空中目标积累时间约2～8 s)而定，选择固定更新频率与应急机制相结合的方式。

4 仿真

下面仿真2维阵列OTHR对某任务的具体选频流程。设雷达接收阵列为矩形阵如图1所示，阵元数和阵元间距在两维均相同，K1=K2=20, d1=d2=15 m。任务区域位于距雷达接收阵列地面rt=1500 km，方位角ϕt=15°处，拟采用带宽B=50 kHz线性调频(Linear Frequency Modulation, LFM)信号，工作频点待确定。

4.1 返回散射电离图

返回散射探测设备发射站扫频6～24 MHz, 2维接收阵列录取数据。取第1行数据进行方位角波束形成及后续处理，得到返回散射电离图如图3所示。初步估计地面距离1500 km对应射线距离在1600 km左右。观察图中在1600 km具有较大幅值的频率约为15 MHz，因此选择14.500～15.500 MHz为频段范围，间隔为B/2=25 kHz，待选频点为f∈F, F=[14.525, 14.550,…,15.450,15.575] MHz。

4.2 电离层射线追踪

设置电离层当前状态。电离层分E层，F1层和F2层。各层临界频率分别为3.700 MHz, 11.650 MHz和12.700 MHz，层高分别为115 km, 190 km和310 km，半厚度分别为15 km, 95 km和100 km。基于MQP电离层模型给出各待选频点f的地面/射线距离-方位角关系图，并统计所有可达任务区域的路径及其对应的俯仰角θfl和射线距离Rfl。

以15.000 MHz为例，俯仰角与地面/射线距离关系如图4所示。可以看到，可到达地面距离覆盖了1500 km，对应射线距离包含E层和F1层反射。因此15.000 MHz有两条射线可到达任务位置(仿真中没有考虑不同层交叉传播)，路径1：射线距离Rf1=1558 km，俯仰角θf1=9.77°；路径2：射线距离Rf2=1532 km，俯仰角θf1=5.62°。

4.3 2维ADBF

图3 扫频返回散射电离图

图4 MQP模型下15.000 MHz的俯仰角与地面/射线距离关系图

图5 2维波束形成方向图

4.4 预测回波强度

对每个待选频点f第l条路径，采用wfl处理返回散射数据f得到时延距离-幅度图，然后从图中读取距离Rfl对应幅度Pfl。依然以f=15.000 MHz为例，为方便观察覆盖率，图7描绘各俯仰角度扫描的处理结果。两条虚线标识俯仰角9.77°和5.62°的时延距离-幅度特性。对照路径1参数可读取Pf1=11.4 dB；对照路径2参数可读取Pf2=12.4 dB。

对所有可选频点f∈F进行以上类似处理、读取和记录，可得在各频点路径的回波强度Pfl如图8中虚线，分别代表E层和F1层路径。可见在不同电离层，预测返回强度随频率变化，那么不可避免地会影响信噪比。

4.5 预测SNR选频

由式(10)预测各频点路径在ADBF和脉冲压缩后信噪比。LFM信号频谱幅度|Sf(ω)|在各频点相同，f−B/2＜ω＜f+B/2。将干扰噪声功率谱Zfl(w)，预测回波强度Pfl和|Sf(ω)|代入式(10)，预测各频点路径的信噪比，如图8中两条实线，分别表示E层和F1层路径。可以看到，实线变化趋势呈现出一致性，与图7中ADBF后干扰噪声功率包络特性趋势相反。受回波强度因素的影响，最优信噪比出现在15 MHz在E层返回路径，约为15 dB。因此，选择OTHR工作频点为15.000 MHz。

最后对选频方法运算时间作一点说明：第1步处理扫频数据用时较长，可独立于其它步并行完成，第2步亦可；第3，第4和第5步属于顺序关系，直接影响选频工作时长，可采用高性能计算机或优化算法以提高运算速度，控制运算时间在1 s内，以保持所录取干扰数据的可参考性。

5 结论

本文提出了2维阵列天波超视距雷达自适应选择工作频率的方法。针对任务区域，考虑各频点散射回波强度及干扰噪声的自适应抑制和特性，选择工作频点优化信号处理后预期信噪比。对选频方法的具体流程进行了仿真，结果表明选频方案可行。此外，关于2维波束形成有两点说明。(1)如果待选频段范围较窄，同电离层反射路径的俯仰角参数相近，待选频点对同层路径可采用相同的波束形成权向量，以减少运算量。(2)如不考虑空域维干扰抑制，以常规波束形成代替自适应波束形成，同样适用于本选频方法。

图6 常规和自适应波束形成后的干扰频谱比较

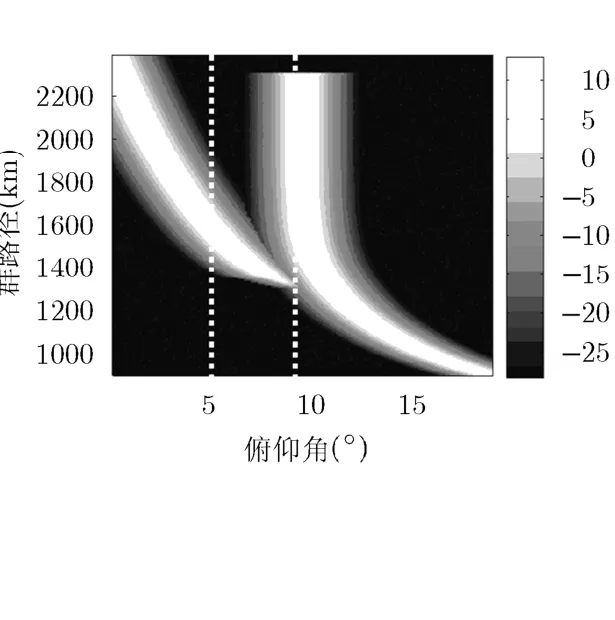
图7 频点15.000 MHz俯仰角群时延特性图

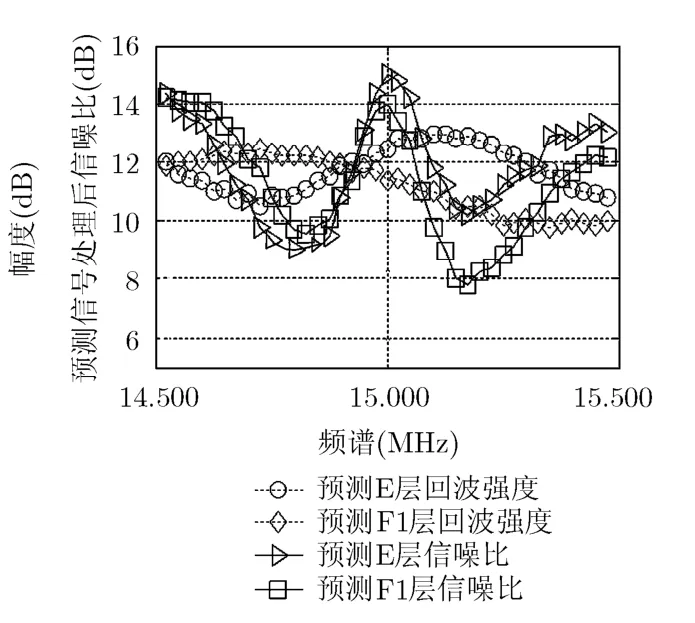
图8 各频点路径预测返回强度和信噪比

[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 7-10.

Zhou Wen-yu and Jiao Pei-nan. Technology in Over The Horizon Radars[M]. Beijing: Publishing House of Electronics Industry, 2008: 7-10.

[2] Earl G and Ward B. Frequency management support for remote sea-state sensing using the JINDALEE skywave radar[J]. IEEE Journal of Oceanic Engineering, 1986, 11(2): 164-173.

[3] 苏洪涛, 保铮, 张守宏. 天波超视距雷达工作频率点的自适应选择[J]. 电子与信息学报, 2005, 27(2): 254-277.

Su Hong-tao, Bao Zheng, and Zhang Shou-hong. Adaptive operating frequency selection for SKW-OTHR[J]. Journal of Electronics & Information Technology, 2005, 27(2): 254-277.

[4] Saverino A L, Capria A, Berizzi F, et al.. Frequency management in HF-OTH skywave radar: ionospheric propagation channel representation[J]. Progress In Electromagnetics Research B, 2013, 50: 97-111.

[5] Bazin V, Molinie J P, Munoz J, et al.. NOSTRADAMUS: an OTH radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2006, 21(10): 3-11.

[6] 吴瑕, 陈建文, 鲍拯, 等. 新体制天波超视距雷达的发展与研究[J]. 宇航学报, 2013, 34(5): 671-678.

Wu Xia, Chen Jian-wen, Bao Zheng, et al.. Development and research on the new system sky-wave over-the-horizon radar[J]. Journal of Astronautics, 2013, 34(5): 671-678.

[7] Saillant S, Auffray G, and Dorey P. Exploitation of elevation angle control for a 2D HF sky wave radar[C]. Proceedings of the International Radar Conference, Adelaide, Australia, 2003: 661-666.

[8] Frazer G J, Abramovich Y I, and Johnson B A. Use of adaptive non-causal transmit beamforming in OTHR: experimental results[C]. Proceedings of the International Radar Conference, Adelaide, Australia, 2008: 311-316.

[9] Abramovich Y I, Frazer G J, and Johnson B A. Principles of mode-selective MIMO OTHR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1839-1868.

[10] Benito E, Bourdillon A, Saillant S, et al.. Inversion of HF backscatter ionograms using elevation scans[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2008, 70(15): 1935-1948.

[11] 王世凯, 焦培南, 柳文. 改进的Kriging技术实时重构区域电离层foF2的分布[J]. 电波科学学报, 2006, 21(2): 166-171.

Wang Shi-kai, Jiao Pei-nan, and Liu Wen. Improved Kriging technique of ionospheric parameter foF2 instantaneous mapping[J]. Chinese Journal of Radio Science, 2006, 21(2): 166-171.

[12] Jiang C, Yang G, Zhao Z, et al.. A method for the automatic calculation of electron density profiles from vertical incidence ionograms[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2014, 107: 20-29.

[13] 姚宜斌, 汤俊, 张良, 等. 电离层三维层析成像的自适应联合迭代重构算法[J]. 地球物理学报, 2014, 57(2): 345-353.

Yao Yi-bing, Tang Jun, Zhang Liang, et al.. An adaptive simultaneous iteration reconstruction technique for three dimensional ionospheric tomography[J]. Chinese Journal of Geophysics, 2014, 57(2): 345-353.

[14] Papazoglou M. Matched-field altitude estimation for

over-the-horizon radar[D]. [Ph.D. dissertation], Duke University, 1998.

[15] 游伟, 何子述, 胡进峰. 基于匹配场处理的天波雷达高度估计算法[J]. 电子与信息学报, 2013, 35(2): 401-405.

You Wei, He Zi-shu, and Hu Jin-feng. Skywave radar altitude estimation algorithm based on matched-field processing[J]. Journal of Electronics & Information Technology, 2013, 35(2): 401-405.

[16] Li J, Du L, and Stoica P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming[C]. Proceedings of IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Las Vegas, USA, 2008: 2325-2328.

[17] Hunsucker D R. An atlas of oblique-incidence high-frequency backscatter ionogram of the midlatitude ionosphere[R]. ESSA Technical Report, U.S. Department of Commerce, Environmental Science Services Administration, Institute for Telecommunication Sciences, 1970.

罗忠涛： 男，1984年生，博士生，研究方向为超视距雷达、多输入多输出(MIMO)雷达信号处理.

何子述： 男，1962年生，博士，教授，博士生导师，目前主要从事天波超视距雷达技术、宽带MIMO数字阵雷达技术的研究.

卢 琨： 男，1977年生，博士，高级工程师，主要从事雷达系统总体设计.

陈绪元： 男，1963年生，高级工程师，研究方向为雷达系统技术、相控阵雷达技术、特种体制雷达技术等.

Operating Frequency Selection for Sky-wave Over-the-horizon Radar with 2-D Array

Luo Zhong-tao①He Zi-shu①Lu Kun②Chen Xu-yuan②

①(School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

②(Nanjing Research Institute of Electronics Technology, Nanjing 210013, China)

This paper presents a method of adaptive operating frequency selection for sky-wave Over-The-Horizon Radar (OTHR) with 2-D array by predicting Signal-to-Noise Ratio (SNR) of paths to the area of interest. With the elevation resolution of 2-D array, this method overcomes the incapability of separating multipath/multimode signals for OTHR with 1-D array. For frequency selecting, firstly, sounding equipments and 2-D array record the backscattering data, environment data and ionosphere state data. Propagation paths to the area of interest are deduced for available frequencies based on the ionosphere model and state. 2-D adaptive digital beam forming is employed to suppress interferences and predict the power of echoes. Finally, the paths' SNR is calculated and the frequency of the maximum SNR is selected as the optimal operating frequency.

Over-The-Horizon Radar (OTHR); Frequency selection; 2-D array

TN958.93

：A

：1009-5896(2015)04-0975-07

10.11999/JEIT140720

2014-05-29收到，2014-09-12改回

国家自然科学基金(61032010, 61102142, 61301262)资助课题

*通信作者：罗忠涛 loztsky@163.com