一种通过结构边界进行贝叶斯网络学习的算法

刘广怡李 鸥 张大龙

(解放军信息工程大学 郑州 450000)

一种通过结构边界进行贝叶斯网络学习的算法

刘广怡*李 鸥 张大龙

(解放军信息工程大学 郑州 450000)

贝叶斯网络是智能算法领域重要的理论工具，其结构学习问题被认为是NP-hard问题。该文通过混合学习算法的方式，从分析低阶条件独立性测试提供的信息入手，给出了构造目标网络结构空间边界的方法，并给出了完整的证明。在此基础上执行打分搜索算法获得最终的网络结构。仿真结果表明该算法与同类算法相比具有更高的精度和更好的执行效率。

贝叶斯网络；结构学习；有向无圈图；条件独立

1 引言

作为人工智能领域表示不确定性知识和推理的一种重要方法，近些年来，贝叶斯网络(Bayesian Network, BN)一直是众多国内外学者研究的热点，目前在诸如故障检测、医疗诊断、交通管理等方面已经取得了成功的运用[1−3]。从贝叶斯网络发展的过程看，一开始人们关注的是寻求一种数据结构以对联合概率密度进行压缩表示，并针对该数据结构开发快速的概率推理算法，因此诞生了贝叶斯网络。在取得成功之后，人们开始转而关注针对数据的网络结构自学习算法研究。本质上看，贝叶斯网络的结构学习问题属于组合优化问题，并已经被证明为NP-hard[4]，尽管如此，一些启发式算法还是得到了成功的应用[5−7]。

目前，BN结构学习算法大致可分为基于独立性测试的方法和基于打分-搜索机制的方法。近来，一些研究者结合上述两种方法提出一类混合算法，该类算法首先利用条件独立测试(ConditionalIndependence testing, CI-testing)降低搜索空间的复杂度，然后执行评分搜索找到最佳网络。这类算法由于有选择性地压缩了搜索空间，因此可以提高结构学习算法整体收敛速度，具有较强的实用性。

对于目前大多数针对贝叶斯网络结构的混合学习算法而言，都是先通过CI测试获得目标网络的局部结构。文献[8]中通过CI测试分析目标网络中可能存在的V结构，但是这种方法需要事先获得网络的框架，这一条件在实际的贝叶斯网络学习中往往不容易获得。文献[9]中提出了一种MMHC(Max-Min Hill Climbing)算法，该算法分为2部分，第1部分称为MMPC(Max-Min Parents and Children)，它通过CI测试获得每个节点的父节点和子节点集，从而给出待学习目标网络的一个局部框架，进而在算法的第2部分执行打分搜索确定网络中存在的边及方向。由于算法的第1部分使用了高阶CI测试，而这种测试的准确性无法保证[10]，因此在搜索阶段并没有严格依据MMPC给出的先验结构，而是进行了相当程度的开放搜索，这样就导致了计算资源的浪费。文献[11]提出了BNEA算法，它是一种基于MMHC和最大主子图分解(Maximal Prime Decomposition, MPD)的方法，通过MMHC给出的节点Markov边界[12]进行MPD，从而在较低的维度上尝试获得网络的Markov等价结构。在一定程度上，BNEA算法获得的Markov等价结构比直接使用MMPC得到的局部结构要精确，但由于调用MMPC算法无法避免高阶CI测试，因此BNEA算法在计算量和精度的平衡上还有待进一步提高。

本文提出基于混合方式的一种上下界候选学习(Upper-lower Bounds Candidate sets Searching, UBCS)算法，该方法首先通过低阶CI测试确定待学习网络结构空间的上下界，从而提供一种更有指导意义的候选网络集，在此基础上使用贪婪搜索算法确定最终的网络结构，仿真结果表明该方法能够在保证精度的同时有效降低学习算法的时间复杂度。

2 相关知识

定义1 贝叶斯网络定义 给定随机变量x1, x2,…,xn的联合分布P，和有向无圈图G=(V,E)，若V={v1,v2,…,vn}与随机变量x1,x2,…,xn一一对应，且(G,P)满足Markov条件[13]，则称二元组BN=(G,P)为一个贝叶斯网络。

2.1 相关定义

由于贝叶斯网络中节点和随机变量一一对应，因此本文中对两者不加区分，除特殊说明外一律统称节点。此外，对于图结构中的有向边vi→vj用eij表示，无向边vi−vj用eij表示，下文不再赘述。

定义2 V结构 贝叶斯网络BN=(G,P)中，∀vi,vj,vk∈V ，若eik∈E, ejk∈E, eij∉E且eji∉E，则称vi,vj,vk构成V结构。

定义3 条件互信息MI(X,Y|Z) 随机变量集(X,Y,Z)的条件互信息MI(X,Y|Z)定义为

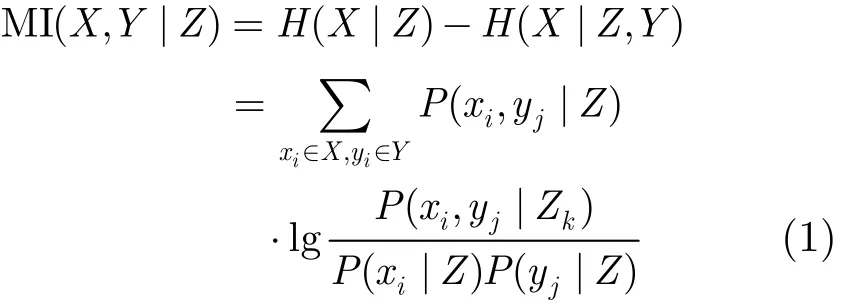
其中

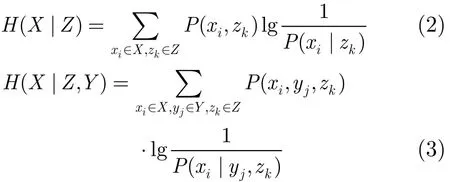
由于MI(X,Y|Z)=0意味着，随机变量集X,Y在给定Z时条件独立，即Ind(X,Y|Z)，因此一般用MI(X,Y|Z)进行随机变量的条件独立测试(CI测试)，并将||Z||称为CI测试的阶数，若Z=Φ，称为0阶CI测试。

定义4 Markov等价 两个具有相同节点集的有向无圈图G1和G2图等价，当且仅当：(1)G1和G2具有相同骨架；(2)G1和G2具有相同的V结构。

称两个贝叶斯网BN1=(G1,P1)和BN2=(G2, P2)Markov等价，若图G1和G2图等价。

按上述关系可以将同一个结点集上的所有有向无环图分成多个等价类，称作Markov等价类，每一个等价类唯一决定一个统计模型，且每一个等价类可以用一个部分有向无环图来表示，称之为完备PDAG。文献[14]给出了Markov等价的特征[14]，文献[15]将此特征扩展到有向无环图，并证明两个有向无环图是Markov等价当且仅当它们有同样的构架，并且有同样的“V”结构。

3 算法描述

贝叶斯网络结构学习算法是在给定数据集D的情况下寻找贝叶斯网BN=(G,P)的最佳网络结。文献[16]证明了包含n个节点可能的BN结构数为

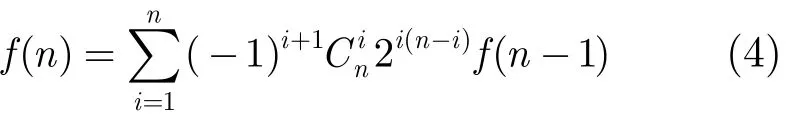
从式(4)可以看出，随着节点的增加，可能的网络结构空间呈指数级增长，因此，寻找好的候选网络结构集是有效降维的办法。基于此，本文给出一种UBCS算法，该算法通过构造目标网络PDAG的上下界给出候选网络集合，并通过打分搜索得到最终网络模型。下文中首先给出UBCS 的第1部分SGLA算法，并证明其输出结果G+是目标网络道德图的上界，之后引入0阶互信息量不增原理，从而给出UBCS 的第2部分LGLA算法，即目标网络PDAG下界的学习算法，在这之后讨论搜索算法。

3.1 候选网络学习算法

首先给出SGLA描述(表1)。

由SGLA算法过程可以知道G+是弦化图，对于弦化图有定理1成立：

定理1 对于任意无向图G，若它是完备PDAG当且仅当G是弦化的。

定理证明参见文献[17]。由定理知G+是完备PDAG，即在最好的情况下，由SGLA算法得到的G+就是目标网络的完备PDAG，但此条件太强，下面给出一个更为一般性的定理。

定理2 给定数据集D，设待求贝叶斯网BN= (G,P)在数据集D下可能的结构为GD，其对应的道德图为GD_m，则由SGLA算法生成的无向图G+是由GD_m构成的偏序集GM=(GD_m,⊆)的上界。

表1 SGLA算法

于∀ejk∈_m,0阶CI测试保证了一定有ejk∈E+；对于∀ejk∈_m，虽然0阶CI测试不能保证一定有ejk∈E+，但SGLA算法第4步保证了此时一定有ejk∈E+。 证毕

定理 3 存在于BN=(G,P)中的任意V结构，一定存在于G+的MPD分解[18]的某一子图中。

定理3的证明参见文献[11]，该定理保证了SGLA输出结果中G,G,…,G覆盖原图所有的V结构，为下文将要给出的LGLA算法提供初始值。

上文讨论了GM=(GD_m,⊆)的上界，从而为搜索提供了可能的备选，下面讨论待学习网络结构空间的下界，从而为搜索算法给出一个较为精确的初始值。

首先引入一个引理：

引理1 对于任意两个离散随机变量vi,vj∈V和V的子集S⊆V/{vi,vj}，有H(vi|vj,S)≤H(vi|vj)成立，等号成立的条件为当且仅当：Ind(vi, vj|S)。

证明从略。

定理4 给定贝叶斯网B=(G,P)，其中G= (V,E)，对于任意vi,vj,vk∈V，有MI(vi,vk)=，其中V′={vi,vj,vk}⊆V成立，如果存在eij∈E,ekj∈E,eik∉E,eki∉E。

证明 由于存在eij∈E,ekj∈E，不失一般性，不妨设MI(vi,vj)=min{MI(vi,vj),MI(vk,vj)}，只需要证明MI(vi,vk)＞MI(vi,vj)，由互信息定义：MI(vi, vk)=H(vi)−H(vi|vk),MI(vi,vj)=H(vi)−H(vi|vj),

则有

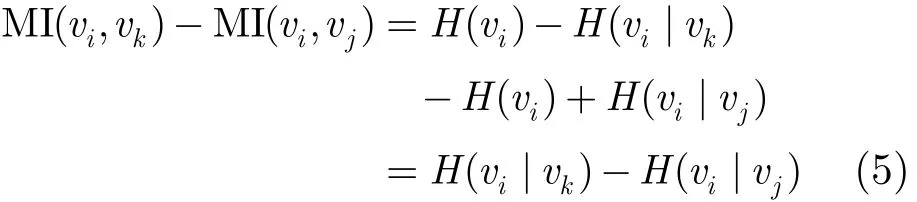
由vi,vj,vk关系可知节点vj∈S，其中S满足Ind(vi,vk|S)，因此式(5)可以写为：

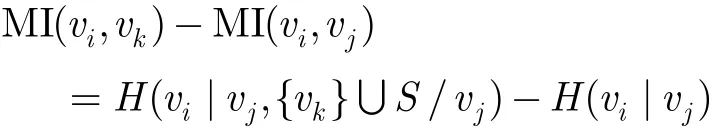
由引理1可得MI(vi,vk)≤MI(vi,vj)，其中等号成立的条件是S/vj=Φ。 证毕

定理4称为0阶互信息量不增性原理。从定理的条件可知，对于存在V结构的情况该定理是不适用的。即对于如图1所示的结构而言，定理4无法判断MI(a,d)和MI(a,b)的大小关系。如果首先在网络中排除所有的V结构，再来考虑节点a和节点cbe的可能连接关系，若MI(a,c)最大，则一定有MI(a,c) =MI(a,b)＞MI(a,e)，此时由1阶CI测试可以直接排除掉ac连接的可能性，因此就能直接确定ab是相连的。通过以上分析可以看出，0阶互信息量不增性原理实际上提供了一种除V结构外的确定网络中无向边存在性的思路。

基于以上分析给出G−学习算法(LGLA)示于表2。

LGLA算法中涉及的V结构测试算法VSTA (V-Structure Test Algorithm)描述如表3所示。

VSTA是一种“尽力而为”的检测算法，由于仅使用了0阶和1阶CI测试，其低阶检测的准确性保证了检测出的V结构的存在性，而对于构成V结构的两个父节点间通路多于一条时，将不予检测。这种检测方式避免了高计算量和干扰边的引入。

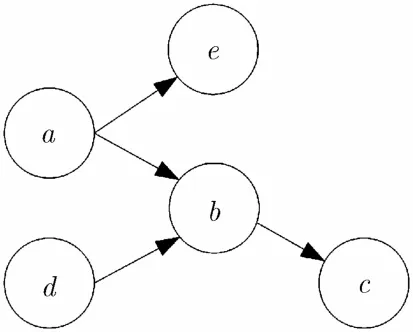
图1 BN中存在V结构的情况

表2 LGLA算法

表3 VSTA算法

对于LGLA的输出结果G−，有定理5成立。

定理 5 设待求贝叶斯网BN=(G,P)中G的所有可能的完备PDAG结构和包含关系构成偏序集PG=(GPDAG,⊆)，则由LGLA算法生成的G−是PDAG。

证明 G−包含有向边和无向边，对于无向边，上文给出的0阶互信息量不增原理保证了对任意无向边eij∈G−[E−]一定有eij∈G[E]成立。G−中的有向边由VSTA给出。由定理3知BN=(G,P)中的任意V结构，一定存在于某个中，由VSTA算法的性质可知任意存在于G−中的V结构一定存在于G中，反之则不一定成立。对于无圈图而言，删除任意有向边得到的仍是无圈图。因此G−是PDAG。

证毕

定理 6 当VSTA返回结果完全准确时，G−是PG的下界。

证明略。

定理 6的条件较强。事实上，在很多情况下，可以近似认为G−是PG的下界。以Asia网络为例。通过图2可以看到，G−中的任意边都存在于原始网络的PDAG中。

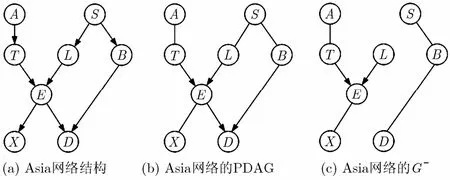
图2 Asia网络结构及其对应的PDAG和G−

3.2 打分搜索学习算法

爬山法是关于贝叶斯网络结构学习中基于打分搜索的一种常用贪婪搜索算法，其搜索算子共有3种：加边、减边和反转边。在UDCS算法中，同样使用爬山搜索算法，只是搜索过程受到SGLA和LGLA算法给出的上下界的限制，即搜索算子产生的新的网络结构如果超出SGLA和LGLA给定的边界，则丢弃该结构。为了避免搜索过快的陷入局部最优结构，引入次优竞争机制，每一轮搜索保留前N个得分最高的结构进入下一轮迭代。原则上N的大小由网络结构的规模决定，网络规模越大，N越大，但过大的次优候选集将导致算法时间复杂度的增加。对于规模如Alarm网络的待学习网络而言，推荐经验值N=10。为了便于与文献[11]中的BENA算法进行比较，采用BDeu评分函数作为搜索的目标函数。

4 实验结果与分析

使用标准的Alarm网络对本算法进行测试，并与BNEA和MMHC算法进行比较。首先比较的是在不同样本数3种算法得到的网络结构的评分，如表 4所示，其中，为了便于对比观察，将评分结果进行了归一化处理，仿真结果示于表4。

表4的结果是重复实验10次的平均结果。从表4中可以看出，UBCS算法得到的网络结构评分在小样本数量下优于BENA和MMHC，随着样本数的增加，3种算法学习出的网络结构评分趋于一致，在样本数达到5000时已经和真实网络的评分非常接近。UBCS算法中包含SGLA和LGLA两个主要算法，其中LGLA中由于VSTA算法并不能充分保证检测结果的真实性，但是从仿真结果来看，对最终学习性能几乎没有影响，这一方面由于SGLA提供的上界具有很高的稳定性，另一方面在受约束的打分搜索学习过程中这种影响被进一步减弱所致。应当指出的是算法在样本数较大时(样本数大于5000以上)容易出现过学习的现象，一般认为过学习现象出现在小样本阶段，但对于如贝叶斯网络结构学习而言的高维组合优化问题，由于组合空间的指数级增长，一般情况下很难使用充分的样本进行学习，且目前的算法在巨大样本数面前所付出的时间性能的代价也是不容忽视的问题，因此，对于维数较高的贝叶斯网络结构学习问题，应当探索在适当样本数下精度和泛化能力平衡的学习算法。UBCS算法中由于SGLA和LGLA的使用对泛化能力起到了一定的保证，因此在学习过程中没有发现过学习现象的发生。

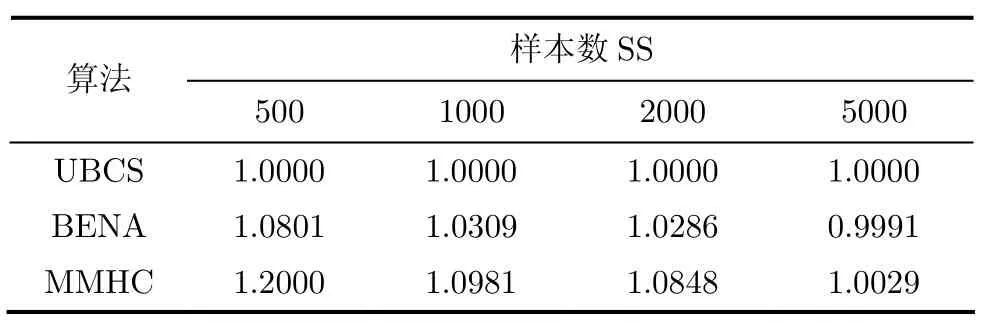
表4 UBCS, BENA, MMHC在Alarm网络数据集上的评分对比

3种算法所消耗的时间如图3算法所示。仿真使用的计算机是主频为2.50 GHz的Intel 4核处理器，内存4G。从图3算法中可以看出，UBCS相比于其他两种算法在时间复杂度上具有明显的优势，与MMHC相比，BNEA和UBCS都使用了MDP分解降低了搜索空间维度，从而压缩了学习时间，而BNEA由于调用了MMHC中的MMPC算法，在最坏情况下BNEA可能与MMHC具有相同的复杂度，BNEA的空间分解从头至尾仅依赖分解空间中的0阶和1阶CI测试，因而具有更好的时间复杂度性能。

5 结束语

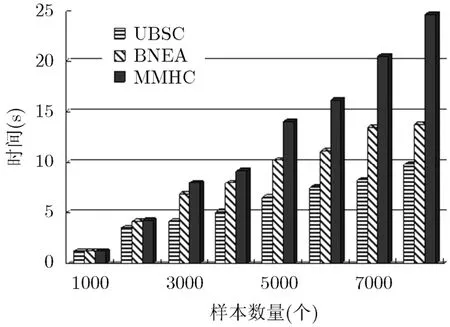
图3 算法时间复杂度比较

本文提出了一种混合方式的贝叶斯网络结构学习算法(UBCS)。该算法利用低阶的CI测试获得待学习网络结构空间的上下界，从而提供一种较好的约束结构，进而通过打分搜索的方式确定网络的最终结构。理论证明和仿真结果都表明了该算法的有效性。与同类混合结构学习算法相比，UBCS算法具有时间复杂度上的明显优势，并可以达到令人较为满意的学习精度。下一步的研究目标为进一步完善UBCS算法中的上下界学习算法(SGLA和LGLA)，并尝试应用到诸如增量学习和不完备数据下的学习等贝叶斯网络结构学习的其他问题中。

[1] Pourali M and Mosleh A. A functional sensor placement optimization method for power systems health monitoring[J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1711-1719.

[2] Andrzej W and Edyta W. Integrating Bayesian networks into fuzzy hypothesis testing problem-case based presentation[C]. 2013 IEEE 15th International Conference on e-Health Networking, Application & Services (Healthcom), Lisbon, 2013: 100-104.

[3] Neumann T, Bohnke, P L, and Tcheumadjeu T. Dynamic representation of the fundamental diagram via Bayesian networks for estimating traffic flows from probe vehicle data[C]. 2013 16th International IEEE Conference on Intelligent Transportation Systems (ITSC), The Hague, 2013: 1870-1875.

[4] Chickering D M, Geiger D, and Heckerman D. Learning Bayesian networks is NP-hard[R]. Technical Report MSRTR-94-17, Microsoft Research, 1994: 1-22.

[5] Carvalho A. A cooperative coevolutionary genetic algorithm for learning bayesian network structures[OL]. http://arxiv. org/abs/1305.6537. 2013: 1131-1138.

[6] Aouay S, Jamoussi S, and Ben Ayed Y. Particle swarm optimization based method for Bayesian Network structure learning[C]. 2013 5th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO), Hammamet, 2013: 1-6.

[7] Basak A, Brinster I, Ma X, et al.. Accelerating Bayesian network parameter learning using Hadoop and MapReduce [C]. Proceedings of the 1st International Workshop on Big Data, Streams and Heterogeneous Source Mining: Algorithms, Systems, Programming Models and Applications, ACM, Beijing, 2012: 101-108.

[8] 贾海洋, 陈娟, 朱允刚, 等. 基于混合方式的贝叶斯网弧定向算法[J]. 电子学报, 2009, 37(8): 1842-1847.

Jia Hai-yang, Chen Juan, and Zhu Yun-gang. A Hybrid method for orienting edges of Bayesian network[J]. Acta Electronica Sinica, 2009, 37(8): 1842-1847.

[9] Tsamardinos I, Brown L F, and Aliferis C F. The max-min hill climbing BN structure learning algorithm[J]. Machine Learning, 2006, 65(1): 31-78.

[10] Wong M L and Leung K S. An efficient data mining method for learning Bayesian networks using an evolutionary algorithm-based hybrid approach[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(4): 378-404.

[11] 朱明敏, 刘三阳, 杨有龙. 基于混合方式的贝叶斯网络等价类学习算法[J]. 电子学报, 2013, 41(1): 98-104.

Zhu Ming-min, Liu San-yang, and Yang You-long. Structural learning bayesian network equivalence classes based on a hybrid method[J]. Acta Electronica Sinica, 2013, 41(1): 98-104.

[12] De Morais S R and Aussem A. A novel Markov boundary based feature subset selection algorithm[J]. Neurocomputing, 2010, 73(4): 578-584.

[13] Neapolian R E. Learning Bayesian Networks [M]. Englewood Cliffs, NJ, US, Prentice-Hall, Inc., 2004: 31-39.

[14] Frydengberg M. The chain graph markov property[J]. Scandinavian Journal of Statistics, 1990, 17(4): 333-353.

[15] Verma T and pearl J. An algorithm for deciding if a set of observed independencies has a causal explanation[C]. Proceedings of the Eighth Annual Conference on Uncertainty in Artificial Intelligence, Stanford, California, 1992: 323-330.

[16] Robinson R W. Counting Unlabeled Acyclic Diagraphs[M]. Berlin Heidelberg, Springer, 1977: 28-43.

[17] Andersson S A, Madigan D, and Perlman M D. A characterization of Markov equivalence classes for acyclic digraphs[J]. The Annals of Statistics, 1997, 25(2): 505-541.

[18] Wu D. Maximal prime subgraph decomposition of Bayesian networks: a relational database perspective[J]. International Journal of Approximate Reasoning, 2007, 46(2): 334-345.

刘广怡： 男，1982年生，博士生，研究方向为网络数据智能处理、智能算法、贝叶斯网络.

李 鸥： 男，1961年生，教授，博士生导师，研究方向为人工智能、计算机网络协议、认知网络.

张大龙： 男，1976年生，博士，讲师，研究方向为网络数据智能处理、网络协议分析.

Learning Bayesian Network from Structure Boundaries

Liu Guang-yi Li Ou Zhang Da-long
(The PLA Information Engineering University, Zhengzhou 450000, China)

Bayesian network is an important theoretical tool in the artificial algorithm field, and learning structure from data is considered as NP-hard. In this article, a hybrid learning method is proposed by starting from analysis of information provided by low-order conditional independence testing. The methods of constructing boundaries of the structure space of the target network are given, as well as the complete theoretical proof. A search & scoring algorithm is operated to find the final structure of the network. Simulation results show that the hybrid learning method proposed in this article has higher learning precision and is more efficient than similar algorithms.

Bayesian Network (BN); Structure learning; Directed acyclic graph; Conditional Independence (CI)

TP18

： A

：1009-5896(2015)04-0894-06

10.11999/JEIT140786

2014-06-17收到，2014-12-20改回

国家科技重大专项(2014ZX03006003)资助课题

*通信作者：刘广怡 liu.guangyi@outlook.com