一种新的高分辨率宽波束机载SAR成像算法
林 雪孟大地李芳芳胡东辉丁赤飚
①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)
②(中国科学院电子学研究所 北京 100190)
③(中国科学院大学 北京 100049)
一种新的高分辨率宽波束机载SAR成像算法
林 雪*①②③孟大地①②李芳芳①②胡东辉①②丁赤飚①②
①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)
②(中国科学院电子学研究所 北京 100190)
③(中国科学院大学 北京 100049)
目前的频域成像算法在应用于高分辨率宽波束机载合成孔径雷达(SAR)时不能精确补偿运动误差,而可以精确成像的时域算法存在计算效率低下的问题。针对上述问题,该文提出一种新的成像算法。该算法通过对信号2维频谱进行扰动操作,将频域与时域算法结合互补,在提高运补精度的同时,也提高了后向投影的计算效率,从而在应用于高分辨率宽波束机载SAR时得到成像精度与效率的平衡。通过仿真和实际数据分析,验证了该算法应用于高分辨率宽波束系统的有效性。
合成孔径雷达;成像算法;高分辨率;宽波束;信号扰动
1 引言
目前,合成孔径雷达(Synthetic Aperture Radar, SAR)的成像算法可以分为两类:一类是基于快速傅里叶变换(FFT)的频域算法,如距离-多普勒(Range Doppler, RD)算法[1]、Chirp Scaling算法[2]、ωK算法[3];另一类是时域(后向投影)算法如后向投影(Back-Projection, BP)算法[4]。其中,频域算法具有高效的计算效率,但在处理机载数据时,需要解决运动补偿的问题。研究者针对该问题提出了一系列运动补偿算法,从前期的采用了波束中心假设的两步运动补偿算法[5],到后来针对方位向空变误差提出的一系列基于分块补偿的相位补偿方法[6−10]。这些方法可以在一定程度上校正运动误差对成像结果的影响,对于窄波束SAR而言,可以得到令人满意的效果。然而,对于宽波束系统而言,分块补偿的局部有效性所带来的误差将会影响成像精度,另外,对于高分辨率宽波束SAR系统而言,由于其距离单元较小、合成孔径时间较长,在载机运动误差较大时,方位空变误差不但导致方位向相位误差,同时导致距离迁移校正误差,这种情况下,上述仅对方位空变相位误差进行补偿的方法不能实现对目标回波信号进行完全积累,从而导致SAR图像分辨率降低,成像质量下降。上述问题在时域算法中都能得以解决。后向投影算法根据图像像素位置计算天线和像素点间的距离延时,将雷达回波数据反向投影到图像域并在每个像素点累加,从而得到2维图像。该算法可完全补偿运动误差,不受波束宽度限制,适用于一般成像几何。BP算法的主要缺点在于其庞大的计算量,对于图像大小为N×N且孔径点数也为N的情况,BP算法将需要量级为3N的运算量。
针对频域与时域算法各自的特点,本文提出一种新的适用于高分辨率宽波束机载SAR的成像算法,意图在精度和效率方面得到平衡。该算法将两类算法结合,通过对经过ωK算法预处理后的2维频域信号进行扰动,改变其方位向调频率,使得扰动后信号其孔径内的采样点数减小,之后对扰动后信号进行后向投影操作来补偿空变误差。由于后向投影操作不仅可以补偿相位误差,同时可以补偿位置误差,因此解决了频域算法不能补偿空变误差导致的距离迁移校正误差的问题;另一方面,由于扰动后信号的孔径内采样点数降低,而后向投影是将孔径内的信号投影回图像域的过程,因此后向投影计算量减小,从而使本算法的计算效率高于时域算法。由上可知,联接两类算法的扰动操作是本文成像算法的可行性关键,考虑到线性调频信号的时频对应特性,通过引入一个线性调频信号对预处理后的数据进行扰动,以达到改变调频率的目的是可行的,详细推导将在后文给出。综上所述,本文算法得到成像精度与计算效率之间的平衡,适用于高分辨率宽波束机载SAR成像。同时,本文算法的保相性能也令人满意,完全可以应用于干涉SAR数据处理。根据本文算法的特点,将其命名为chirp扰动的后向投影(Chirp Perturbed Back Projection, CPBP)算法。
本文内容安排为:引言介绍SAR成像算法的研究背景;第2节对SAR回波进行简单建模;第3节详细阐述所提成像算法(CPBP算法),给出存在运动误差情况下的信号频谱形式,并讨论引入扰动信号的必要性,CPBP算法的参数设置及计算量也在这一部分进行分析说明;第4节通过仿真和实际数据对CPBP算法进行验证,与标准BP算法的对比证明了CPBP算法的有效性;最后是总结和展望。
2 SAR回波模型
如图1所示的3维直角坐标系,设某一理想点目标其坐标为p(xi,yj,Zij),传感器所在位置为P(x(η),y(η),z(η)), η表示方位时刻,存在运动误差情况下,经过解调后的雷达接收回波信号为
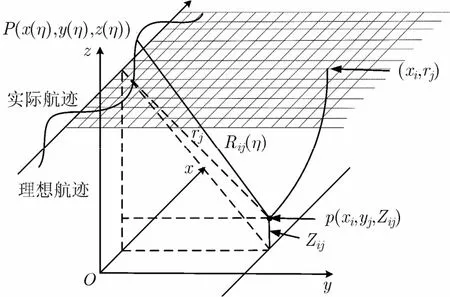
图1 SAR成像几何
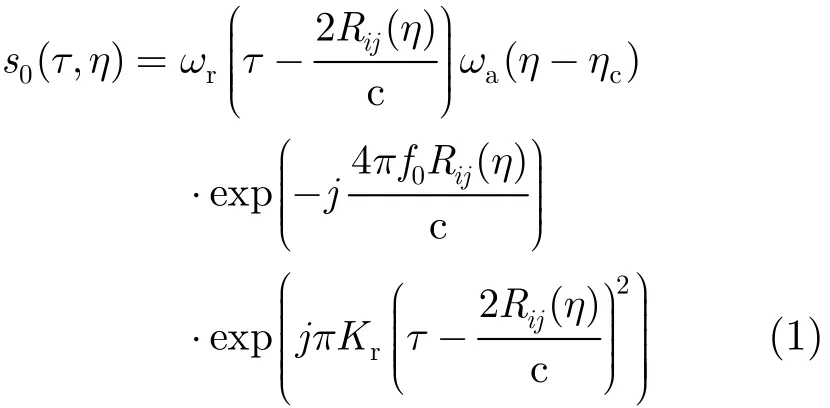
其中,τ表示距离时间延迟,c代表光速,f0表示雷达工作频率,Kr代表距离调频率,ωr(·)与ωa(·)分别表示发射脉冲包络以及双程波束方向图,Rij(η)=表示传感器到点目标的实际距离历程。该距离历程与理想轨迹下的距离历程存在一个误差值,于是,传感器到点目标的实际距离历程可表示为Rij(η)=R(η)+ Rne(η)+Re(η),其中,R(η)表示理想距离历程,Rne(η)表示空不变斜距误差,Re(η)表示空变斜距误差。后续的算法研究与阐述都是基于这一回波模型展开的。
3 CPBP算法
3.1 预处理
不失一般性,本文假设系统工作在正侧视模式。利用驻定相位原理(Principle Of Stationary Phase, POSP),得到用频域方法进行距离压缩并引入直接运补算法(Direct Motion-compensation Algorithm, DMA)[11]运动补偿后的信号为
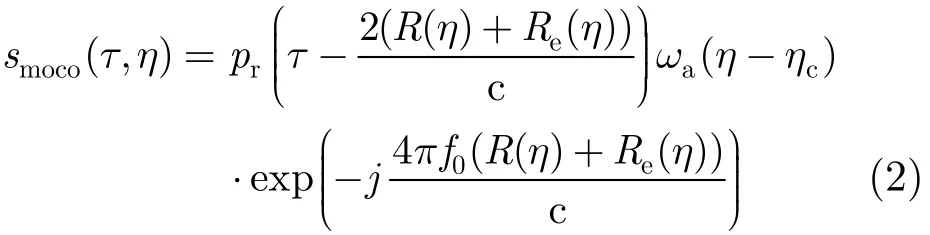
其中pr(τ)=IFFT(ωr(fτ/Kr))。文中选择DMA作为空不变运补算法的原因,一方面在于其可以直接应用于ωK算法,无需作额外调整[12];另一方面在于经过DMA算法后的残余误差更小[11],从而使后续操作更为精确。利用POSP并令,其中Vr表示载机速度,得到式(2)所示信号Stolt插值后的2维频谱表达式。
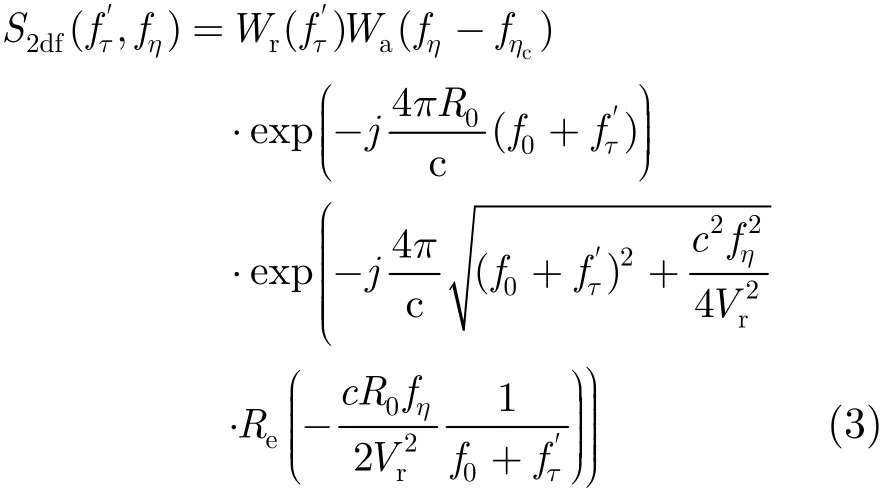
3.2 信号扰动
根据线性调频信号的时频对应特性,对一给定的线性调频信号,通过与另一线性调频信号相乘,可达到改变调频率的效果,本文称之为chirp扰动。观察式(3)中信号方位包络可知,其存在距离方位耦
合问题,而后续的后向投影操作需要满足时域与频域信号坐标的一一对应关系,因此需要消除数据中存在的距离方位耦合。为解决这一问题,本文通过构造一个调频率随距离频率变化的方位调频信号作为扰动信号来对3.1节中得到的2维频域信号进行扰动,从而在改变时域信号长度的同时消除距离与方位的耦合。
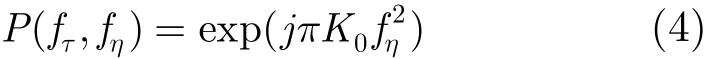
将该扰动信号与2维频域信号相乘,之后进行傅里叶逆变换,整理得到经过扰动后的时域信号表达式为

3.3 后向投影
对比扰动后时域信号式(5)与扰动前距离压缩信号式(2)可知,上述预处理及扰动操作实际上相当于对信号做了映射。经过该映射后的信号,其合成孔径内方位采样点位置有了相应变化。以像素点
(xi,rj)为例,扰动前该点对应信号的回波域位置为,其中ηij∈, R(τij)为像素点(xi,rj)的最近斜距。经过扰动,像素点对应信号的距离延时映射为,方位向累积范围改变为。通过对参数a的调节,使得该像素的回波数据在回波域中的方位向采样点数减小,从而可以达到减少计算量,提高计算效率的目的。由于本文算法在预处理过程中进行的是方位空不变运动补偿,因此相对应的,该算法的扰动和后向投影操作部分也可认为是一种后处理的方位空变运动补偿算法。
综上所述,扰动后信号的后向投影过程可以描述为:对于像素点(xi,rj),在回波域中寻找位置在的能量进行相干累加,从而得到像素点(xi,rj)的复数灰度值。为补偿扰动操作对于信号相位的影响,在相干累加之前需要对这些位置的数据进行相位校正,具体操作为
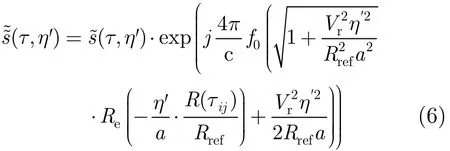
至此,完成了CPBP算法的所有步骤。综合前文所述,CPBP算法整体流程可由图 2直观表示。其中ωK+DMA表示预处理采用的是引入了DMA的ωK算法而得到2维频谱。
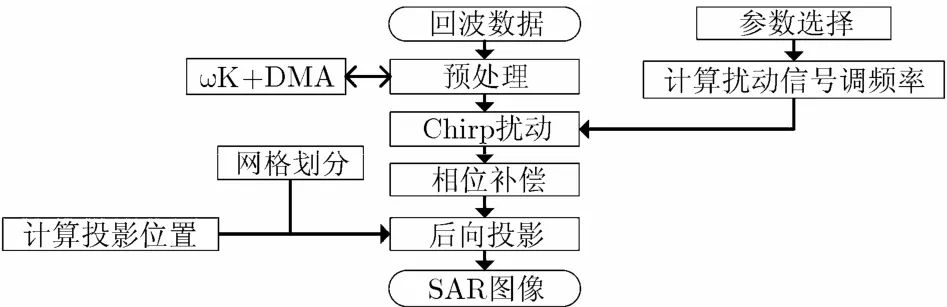
图2 CPBP 算法流程
3.4 参数设置与计算量分析
3.4.1 算法误差分析 本文算法的误差主要来源于两方面:一方面来源于2维频谱信号表达式推导过程中对空变误差的近似。针对该误差,本文采用了DMA进行空不变运动补偿,使得该误差相比采用两步运动补偿算法而言更小,从而减小其对整体算法的精度影响。另一方面,在后向投影过程中,孔径内采样点的减少实际上相当于对扰动前信号做了降采样,由于残余误差与信号是共存的,因此在该过程中对残余误差也进行了降采样,从而引入误差。该误差随参数a的增大而减小,因此,从算法精度方面考虑,不建议将参数a设置的过小。
3.4.2 计算量分析 计算量方面,由于扰动过程仅需要进行一个乘法运算和IFFT,而后向投影过程是逐点计算,因此本成像算法的计算量主要来源于后者。回顾3.2节中对扰动后信号的合成孔径时间的描述=θbw·aRref/Vr,并令雷达脉冲重复频率为PRF,则对于一幅M×N的图像,CPBP算法的运算量可以表示为
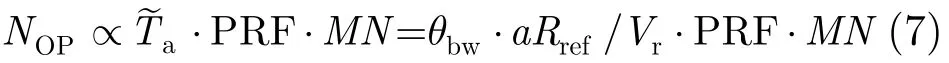
3.4.3 参数设置 3.2节中提到,分析中所采用的调频率表达方式是为了便于对扰动操作的理解,即可以认为扰动操作是对坐标进行了一个系数为aRref/R(τ)的映射。在实际处理中,本文采用一个可以更直观的体现出计算量的参数——扰动后信号的时间带宽积A=a·fdop来对扰动信号进行表示,其中fdop表示方位多普勒带宽。该参数A的大小正比于扰动后信号的孔径内方位向采样点数,二者仅相差一个常数因子PRF/fdop,因此便于掌握参数设置对算法运算量的影响。采用参数A表达的计算量为
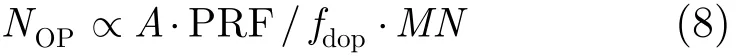
与参数a相同,参数A取值越小,算法的计算量越小,计算效率越高,但同时计算精度下降,因此参数A不能取值过小。同时,由于在扰动操作的表达式推导过程中采用了POSP,而当时间带宽积大于100时,POSP已足够精确[13],因此通常令参数A的值大于100。综合考虑计算效率与精度,对于轨迹误差在10 m量级的情况,参数A取200到600通常可以得到令人满意的结果。
4 实验分析
4.1 仿真数据实验分析
本文采用表1所示的系统参数进行点目标回波仿真,9个点目标均匀分布在场景当中,载机运动误差如图3所示。采用不同成像算法对该回波进行成像处理,对成像结果进行分析说明。
图4(a)展示了进行DMA运动补偿且未进行空变运动补偿情况下的ωK算法成像结果。图4(b)表示采用引入了DMA空不变运补和PTA空变运动补偿算法的ωK算法成像结果。本文所提出的CPBP成像算法得到的成像结果如图4(c)所示(参数A取500),而标准BP算法得到的成像结果作为理想参考值如图4(d)所示。对比图4(a)与图4(b)或图4(c)可知,引入空变运补后的聚焦效果明显改善。对比图4(b), 4(c), 4(d)可以看出,本文提出的CPBP算法所得到的成像结果较引入PTA的的ωK算法更为精确,与标准BP算法的成像结果相当。
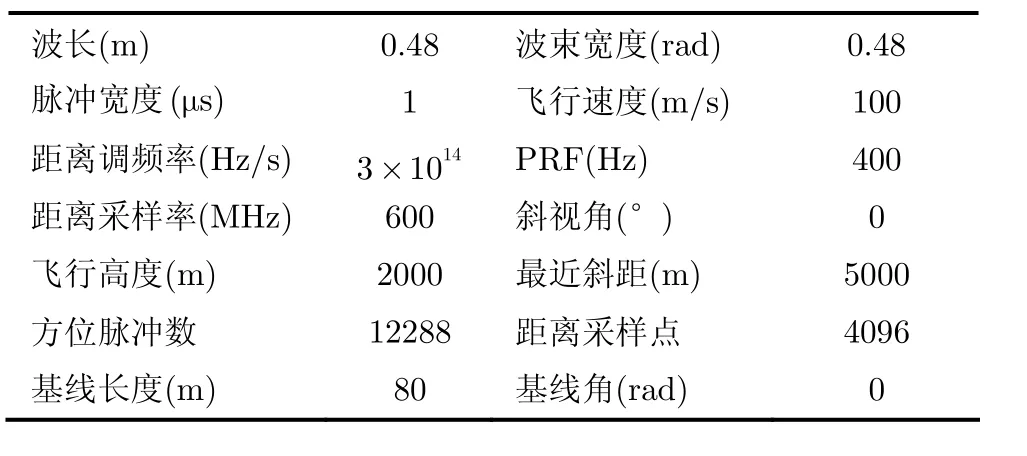
表1 仿真系统参数
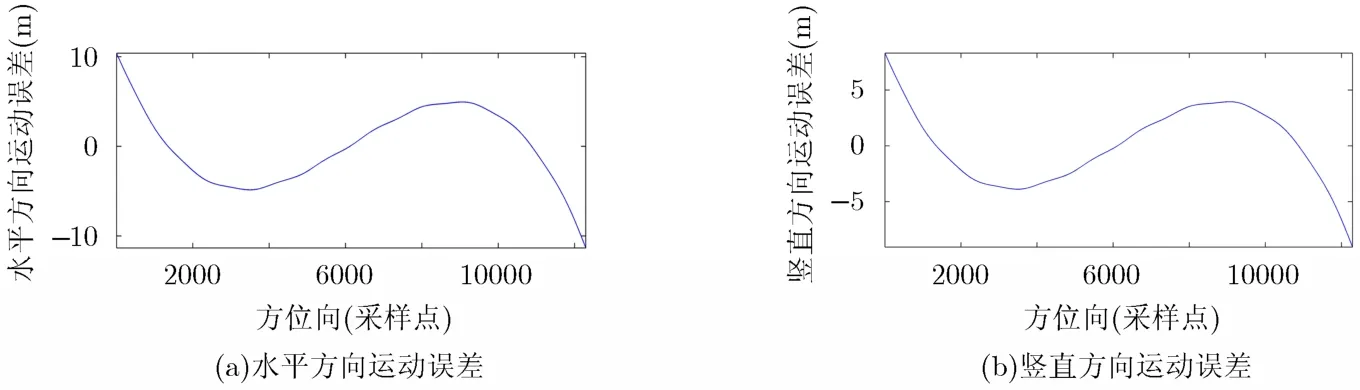
图3 载机运动误差
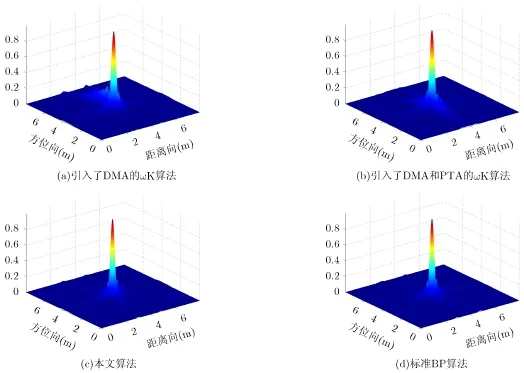
图4 成像结果
图5给出了引入PTA(Precise Topography and Aperture-dependent)的ωK算法、本文算法及标准BP算法所得到的成像结果的方位及距离剖面图。表2给出了本文算法得到的成像结果的测试指标。由图5可以更清晰的看出,本文算法与标准BP算法得到的成像结果相当,而较ωK算法更为精确,因此在大运动误差的情况下,其更适用于高精度宽波束机载SAR系统。同时,由表2各测试指标可知,本文算法的成像结果接近理想值,满足成像精度要求。
图6给出了参数A不同取值情况下,本文算法得到的各点高程误差,可见,其误差在0.3 m以内,符合P波段数字高程模型(Digital Elevation Model, DEM)精度要求(参考德国宇航中心达到的6 m DEM精度[14,15])。注意到误差随斜距增大略有增加,这是由CPBP算法在后向投影过程中引入的误差对于远距目标而言会相对略大造成的,如3.4.1节中误差分析所述,后向投影过程中孔径内采样点的减少实际上相当于对原始信号做了降采样,且去除了距离方位耦合的信号,其降采样后近距与远距目标点的孔径内采样点数相同,因此远距的降采样倍数要略大于近距,从而引入的误差也略大,但由结果可知,其仍满足精度要求。
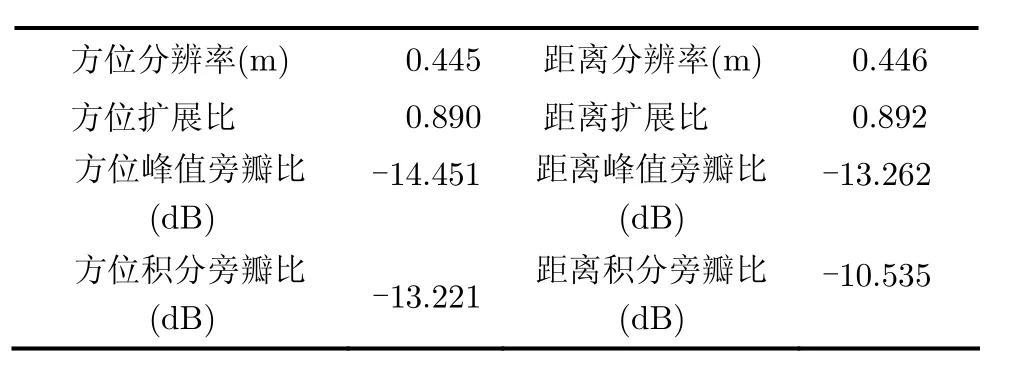
表2 CPBP点目标指标测试结果
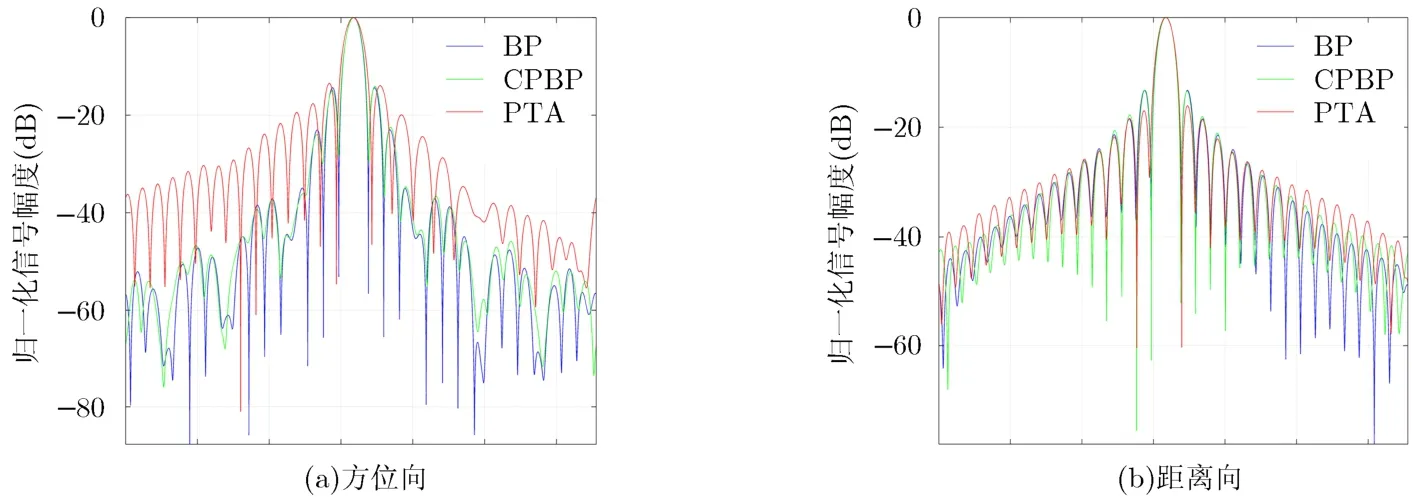
图5 剖面图
如3.4.3节所述,对参数A进行选取时,需综合考虑成像精度与运算效率。本文对不同参数取值条件下本文算法的表现进行了对比分析。图7(a)显示了参数A取值为100至1000时,采用本文算法成像所得到的点目标分辨率。由图可以看出,距离向分辨率基本不变,而方位向分辨率随A取值增大而变好,这同样是由于上文所述的降采样作用引起的。根据系统参数计算得到,方位向理论分辨率为0.443,结合图7(a),参数A取值在400到1000之间时的成像结果已足够精确。图7(b)显示了标准BP算法成像与CPBP算法成像所需时间的比值,该时间比较理论值略小,原因在于成像区域部分像素点并非全孔径成像,扩大方位向成像区域,使得全孔径成像点数增加,则实际值将更接近理论值。结合图7(a)与图7(b),即结合成像质量与运算效率考虑,参数A取值在400到800之间较为合适。
4.2 实际数据实验分析
本文采用中国科学院电子学研究所研制的P波段全极化机载SAR系统采集的数据进行测试。本文选取了一块包含定标场的长度约5 km的区域进行对比分析,选用数据为HH极化数据。获取该雷达数据的P波段机载SAR系统参数由表3给出。
图8和图9分别展示了采用标准BP和本文成像算法得到的成像结果。可以看出,二者成像结果非常相近。图10给出了红色椭圆圈出的区域中,以标准BP算法所得结果为参考,各定标点的高程偏差,其误差在0.15 m以内,满足P波段DEM精度要求。
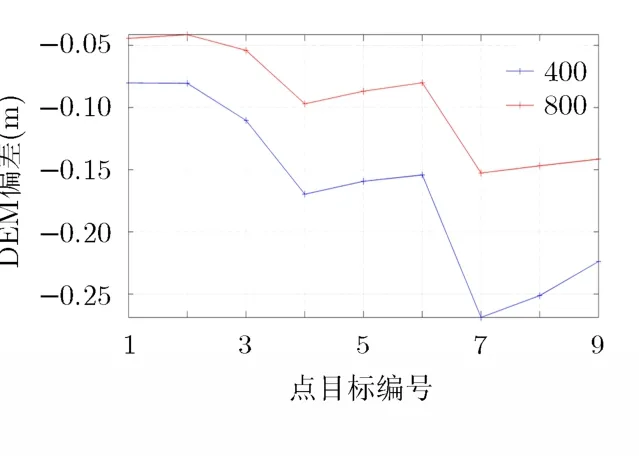
图6 目标高程偏差(从近距到远距)

图7 不同参数取值下成像精度与时间对比
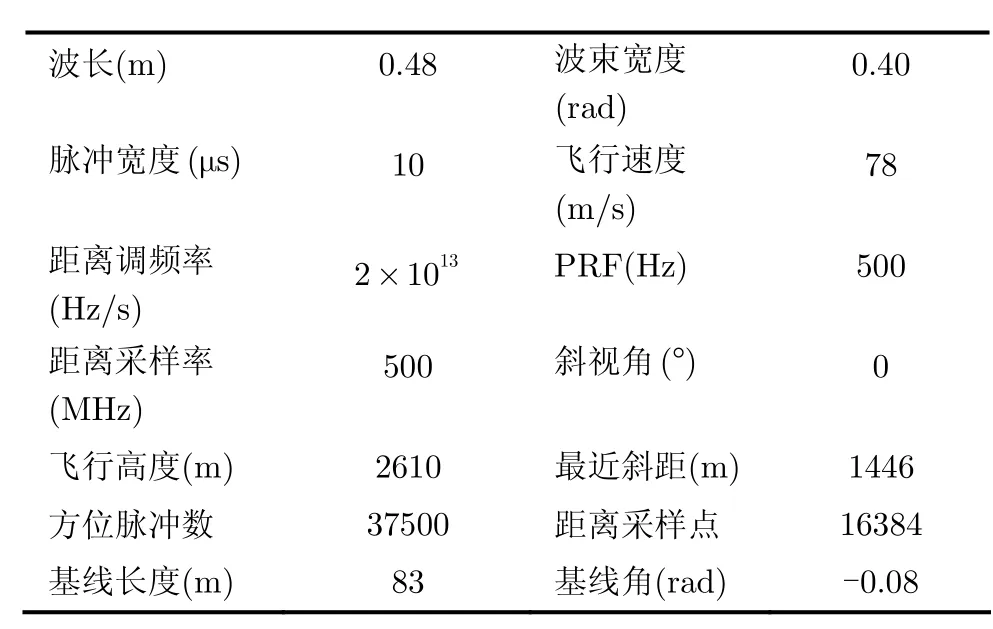
表3 P波段机载重轨干涉SAR系统参数
5 结束语
本文提出了一种新的适用于高分辨率宽波束机载SAR的成像算法。该算法针对频域与时域算法中
各自存在的问题,通过将二者结合互补来得到一种在精度和效率方面都能令人满意的算法。该算法的关键步骤在于信号扰动处理,通过引入一个调频率随距离频率改变的方位向扰动信号,使得扰动后的信号在合成孔径时间内的采样点数下降,同时避免了距离方位耦合,最终达到提高计算效率的目的。文章通过仿真和实测数据实验得到,本文算法的成像精度与标准BP算法相当,且有良好的保相性,用于干涉处理时可以满足DEM精度要求。同时,由本文算法与标准BP算法的运算量对比分析可以看出,本文算法运用在宽波束雷达系统中时,效率较标准算法有一定提升。因此,本文所提出的成像算法在精度与效率之间可以达到一个较好的平衡。后续研究将尝试该算法在更多模式中的应用,例如在双站模式[16]中的应用等。

图8 成像地区BP成像结果

图9 成像地区CPBP成像结果
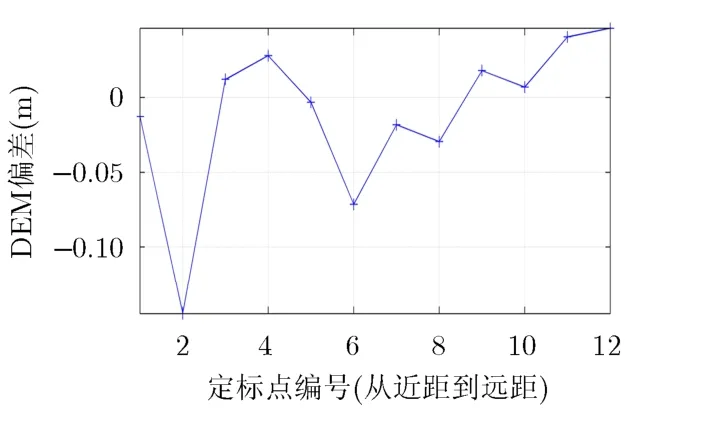
图10 各定标点高程偏差
[1] Smith A M. A new approach to range Doppler SAR processing[J]. International Journal of Remote Sensing, 1991, 12(2): 235-251.
[2] Raney R K, Runge H, Bamler R, et al.. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 786-799.
[3] Cafforio C, Prati C, and Rocca F. Full resolution focusing of SEASAT SAR images in the frequency-wavenumber domain[J]. International Journal of Remote Sensing, 1991, 12(3): 491-510.
[4] Desai M D and Jenkins W K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar[J]. IEEE Transactions on Image Processing, 1992, 1(4): 505-517.
[5] Moreira A and Huang Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1029-1040.
[6] Prats P, Reigber A, and Mallorqui J J. Topographydependent motion compensation for repeat-pass interferometric SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 206-210.
[7] de Macedo K A C and Scheiber R. Precise topography-and aperture-dependent motion compensation for airborne SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 172-176.
[8] Reigber A, Scheiber R, Jager M, et al.. Very-high-resolution airborne synthetic aperture radar imaging: signal processing and applications[J]. Proceedings of the IEEE, 2013, 101(3): 759-783.
[9] Zamparelli V, Perna S, and Fornaro G. An improved topography and aperture dependent motion compensation algorithm[C]. Proceedings of the International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 5805-5808.
[10] Li Y, Xiang X, Ding C, et al.. Improvements to the frequency division-based subaperture algorithm for motion compensation in wide-beam SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1219-1223.
[11] Meng Da-di, Hu Dong-hui, and Ding Chi-biao. A new approach to airborne high resolution SAR motion compensation for large trajectory deviations[J]. Chinese Journal of Electronics, 2012, 21(4): 764-769.
[12] Reigber A, Alivizatos E, Potsis A, et al.. Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation[J]. IEE Proceedings of Radar, Sonar and Navigation, 2006, 153(3): 301-310.
[13] Fachel P H, Ghigha D C, and Jakowatz C, Jr.. Speckle processing method for synthetic-aperture-radar phase correction[J]. Optical Letters, 1989, 14(1): 1-3.
[14] Reigber A, Mercer B, Prats P, et al.. Spectral diversity methods applied to DEM generation from repeat-pass P-band InSAR[C]. Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 16-18.
[15] 钟雪莲. 机载重轨干涉SAR残余运动估计方法研究[D]. [博士论文], 中国科学院电子学研究所, 2011.
Zhong Xue-lian. Residual motion estimation for airborne repeat-pass interferometric SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011.
[16] Dai C, Zhang X, and Shi J. Range cell migration correction for bistatic SAR image formation[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 124-128.
林 雪: 女,1986年生,博士生,研究方向为干涉SAR信号处理.
孟大地: 男,1979年生,副研究员,研究方向为SAR信号处理.
李芳芳: 女,1986年生,博士,研究方向为干涉SAR信号处理.
A Novel Imaging Algorithm for High-precision and Wide-beam Airborne SAR
Lin Xue①②③Meng Da-di①②Li Fang-fang①②Hu Dong-hui①②Ding Chi-biao①②
①(Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Chinese Academy of Sciences, Beijing 100190, China)
②(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
③(University of Chinese Academy of Sciences, Beijing 100049, China)
When applying to a high-precision and wide-beam airborne SAR, the frequency domain imaging algorithms are incapable of accurate Motion Compensation (MoCo), while the precise time domain approaches have the drawback of heavy computation burden. A novel imaging algorithm is proposed to figure out the problem, which combined the frequency domain methods and the time domain ones through a perturbation operation to the two-dimensional spectrum of the signal. The algorithm improves the MoCo precision with the computation efficiency being ameliorated as well, thus balancing the accuracy and efficiency when implements on the high-precision and wide-beam airborne SAR. The results of the simulation and real data are used to validate the effectiveness of the proposed algorithm in application to the high-precision and wide-beam airborne SAR.
SAR; Imaging algorithm; High-precision; Wide-beam; Signal perturbation
TN957.52
: A
:1009-5896(2015)04-0939-07
10.11999/JEIT140685
2014-05-23收到,2014-09-11改回
国家863计划项目(2007AA120302)和国家自然科学基金(61101200, 61401428)资助课题
*通信作者:林雪 linxue862002@163.com

