一种基于稀疏分解的窄带信号频率估计算法

沈志博 董春曦黄 龙 赵国庆

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室 西安 710071)

一种基于稀疏分解的窄带信号频率估计算法

沈志博 董春曦*黄 龙 赵国庆

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室 西安 710071)

针对窄带多分量信号频率估计问题，该文提出一种基于稀疏分解的频率估计算法，能够同时对多个窄带信号的频率进行估计。首先利用传统方法进行频率预估计，然后根据频率预估计的结果建立冗余字典，对信号进行稀疏表示，最后通过匹配追踪算法得到精确的频率估计。该算法极大地减小了字典的长度和稀疏分解的运算量，而且在迭代过程中利用了全局信息更新残差向量，估计结果更为精确，在低信噪比情况下性能也较为稳健。仿真结果验证该算法的有效性和正确性。

信号处理；频率估计；稀疏分解；冗余字典；稀疏表示

1 引言

信号的频率是电子侦察中需要获取的最为重要的参数，它反映了雷达的功能与用途，是信号分选和威胁识别的重要依据[1]。由于电子侦察面对的是非合作信号，接收机往往会瞬时覆盖较大的频率范围[2]，因此，如何对宽频段内的多个窄带信号频率进行有效的估计显得尤为重要[3−5]。目前频率估计算法主要分为非参数法和参数法两大类。非参数法主要是以离散傅里叶变换(Discrete Fourier Transfer, DFT)为基础的，物理意义明确，但是存在能量泄漏和栅栏效应，且算法精度和分辨能力主要依赖于信号长度[6]。参数法中最大似然法[7]虽然能够达到理论上的最优性能，但是需要多维非线性优化，计算量很大，难以实际应用。基于Levinson-Durbin递推的自回归(AutoRegressive, AR)模型法[8]虽然避免了矩阵求逆，减小了计算量，但是受信号初相的影响较大，在分析短序列时会出现谱偏移，谱线分裂的现象，且阶数难以确定，阶数过低，谱峰不明显，而过高的阶数会产生虚假谱峰；以多重信号分类(MUltiple SIgnal Classification, MUSIC)算法[9]和旋转不变技术估计信号参数(Estimating Signal Parameters via Rotational Invariance Techniques, ESPRIT)算法[10]为代表的子空间分解算法利用信号子空间和噪声子空间的正交性，提取信号子空间，在信噪比较高时能够得到较好的估计性能，而在信噪比较低时，估计误差会明显增大。近年来稀疏分解理论得到了广泛的应用[11−13]，通过建立频率冗余字典[14−16]寻求最优匹配原子，再利用稀疏向量中非零元素的位置信息估计信号的各频率分量[17,18]。但是这种方法随着估计精度的提高，字典的长度会急剧增加，稀疏分解难度增大，且由于原子间相互干扰，导致匹配错误的概率也会增加，影响了算法的稳定性。

针对上述问题，本文将传统的频率估计方法与稀疏分解理论相结合，提出一种新的窄带信号频率估计方法。算法利用传统方法的频率预估计的结果构建冗余字典，极大地减小了字典的长度，并对匹配追踪算法求解稀疏系数的过程进行了改进，在迭代过程中利用预估计的结果更新残差向量，使得算法具有更高的估计精度和稳健的性能。

2 稀疏表示模型

假设信号由p个不同频率的复指数正弦信号叠加而成，信号长度为N，则其离散数学模型为

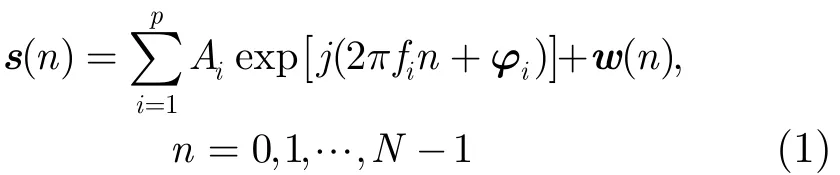
式中，iA,fi,ϕi分别为第i个信号的幅度、频率和初始相位；w(n)为高斯白噪声。

由于信号由多个窄带信号叠加构成，在频域具有良好的稀疏性，所以可以在频域对其进行稀疏表示。在频域建立N×Ns维冗余字典D：

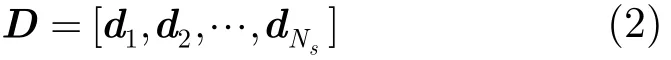
式中，Ns为字典长度，di=[1,ej2πfi·1,…,ej2πfi·(N −1)]T为字典中的第i个原子，那么信号s(n)就可以表示为

式中，s =[s(0),s(1),…,s(N −1)]T,n为N×1维高斯白噪声，z为Ns×1维稀疏系数，在z中只有p个非零值，且对应于信号的幅度。由于z是p稀疏的

(p＜＜Ns)，可以转化式(4)的优化模型：

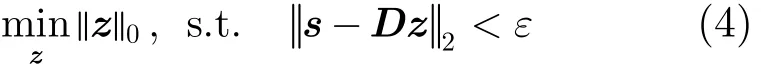
直接求解式(4)是一个非确定性多项式问题(Non-deterministic Polynomial Hard, NP-hard)，可以将优化目标用l1范数来代替[19]，这就将式(4)的优化问题变成了一个凸优化问题，方便求解。

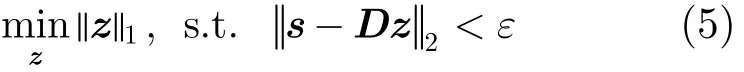
最后根据z中非零值的位置得到p个窄带信号的频率估计。正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)算法[20]通过每次在字典中搜索与残余信号相关性最大的原子来匹配出p个原子，求出稀疏系数确定频率。显然，字典的长度影响着稀疏分解的难度和计算量，Ns越大，迭代过程就越复杂；而且由于OMP算法每次迭代都只是从冗余字典中选择一个与残余信号最佳匹配的原子，对于整个信号而言每次匹配结果很可能只是局部最优解。如果在迭代过程中某一次选错了原子，那么接下来的迭代也会受到影响，最终造成分解结果不是最佳的稀疏解或者误差较大。当字典长度增加时，也会增大这种误匹配的概率，造成频率估计错误。

3 算法原理及步骤

经过以上分析可知，OMP算法进行稀疏分解估计信号频率时主要存在两个问题：一是字典长度增加导致稀疏分解困难；二是迭代过程中的误匹配问题。现在考虑将传统的频率估计方法与OMP算法的迭代过程中的原子匹配过程进行融合，即采用传统方法(FFT, ESPRIT等)进行频率预估计，在估计出的频率附近构建冗余字典可以有效地减小字典的长度；而将每次频率的预估计值嵌入到OMP算法的迭代过程中，则可以在一定程度上减小误匹配的概率。

3.1 冗余字典构建

首先用传统算法对信号频率进行预估计，得到p个信号频率的估计值，然后在每个估计出的频点附近Δf范围内进行等间隔划分，q为划分的网格数，构造子字典D(fi)，并将多个子字典联成一个冗余字典D

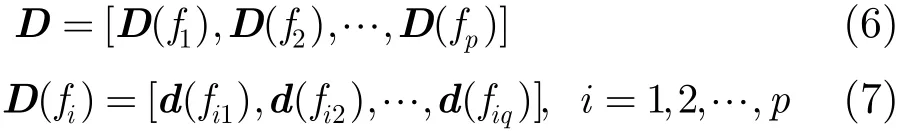
式中，d(fij)=[1,ej2πfij·1,…,ej2πfij·(N−1)]T,j=1,2,…,q表示第i个子字典中的第j个原子，每个子字典D(fi)的维数为N×q，总的冗余字典的D维数为N×L(L=pq)。

3.2 稀疏分解

OMP算法在第m次迭代过程中计算当前残差向量rm−1与字典D中各原子的相关性，选出最佳匹配原子(D中的某一列)，加入到已选出的原子集合Ωm−1中，并计算原信号s在集合Ωm中的正交投影，得到投影系数zm，更新下一次迭代的残差rm。

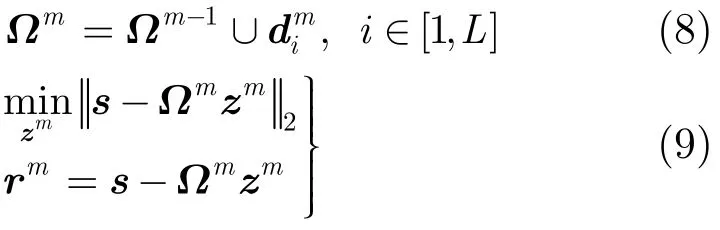
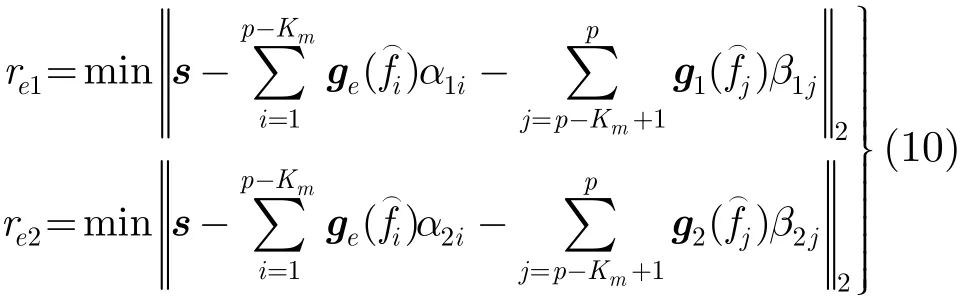
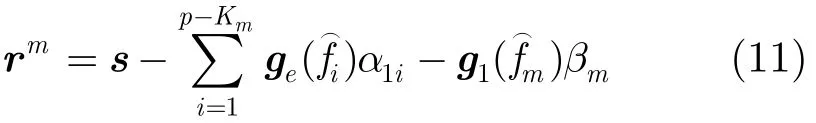
式中，g1()为投影系数βm所对应的原子。

3.3 算法具体步骤

具体的基于频率预估计的稀疏分解算法步骤如表1所示。

表1 基于频率预估计的稀疏分解算法步骤

4 算法性能分析

算法利用了传统方法的估计结果构建冗余字典，即在已经估计出来的p个信号的频率附近Δf范围内进行等间隔划分，划分的网格数取决于期望达到的精度δf,q=Δf/δf 。与传统的直接在测频范围内等间隔划分相比，在达到相同的测频精度的情况下，字典的长度大大减小。OMP算法的计算量为O(k2n)，在稀疏度k(这里等于信号个数)确定时，运算量与字典的长度n成正比，表2给出了不同的冗余字典构建方法计算量的比较。

表2 冗余字典不同构建方法的计算量比较

若测频范围为1 GHz，取δf=0.1 MHz,p=5，则直接构建字典需要的字典长度Ns=104，稀疏分解运算量为O(2.5×105)，且随着测频范围的增加，字典长度和运算量还会增加；而采用频率预估计构建字典，取Δf=5 MHz，则需要的字典长度仅为250，稀疏分解运算量为O(6.25×103)，且与测频范围无关，只取决于信号个数p和测频精度δf。由此可见，采用频率预估计的方法动态构建冗余字典可以有效地减小字典的长度，降低稀疏分解的运算量。

算法将传统方法的频率估计和OMP算法的迭代过程中的原子匹配进行了融合，OMP算法每次迭代是通过寻找字典中与残差向量相关性最大的原子来确定某一个信号的频率值，这可以看成是一种利用局部信息得到的最优解，而对每次残差向量进行频率预估计却能提供全部的频率估计值，相当于一种全局信息，利用这种全局信息来寻找新的匹配原子以及残差向量的更新获得的全局范围内的最优解，因此能够获得更好的估计性能。另外，若在某一次迭代过程中发生原子匹配错误，则re2必然会大于re1，这时就会自适应地采用集合F1作为正交投影空间，利用F1中频率所对应的原子张成的子空间下的正交投影系数来更新残差向量，因此，通过比较正交投影误差re1和re2也可以减小迭代过程中由于原子匹配错误带来的影响。

由于字典是根据频率预估计的结果构建的，因此，预估计误差也会对最终的估计结果产生一定的影响。当频率预估计精度较高时，算法会自适应地采用集合F1作为正交投影空间，更新残差进行下一次迭代，最终频率估计精度主要取决于频率预估计精度。当预估计精度不高时，分为两种情况：一是预估计误差小于Δf/2，此时根据预估计值建立的字典中包含与真实频率最为匹配的原子，算法会采用集合F2作为正交投影空间，更新残差进行下一次迭代，因此，这种情况下，仍能得到频率的正确估计，估计误差主要受字典划分间隔影响；二是预估计误差大于Δf/2时，则根据预估计值建立的字典中不会包含与真实频率最为匹配的原子，只能找到相对匹配的原子，而且随着预估计误差的增大，最终估计误差也会变大。这种情况下，过大的预估计误差(或预估计错误)会导致原子失配而无法得到正确的估计结果。因此，实际中在选择字典范围Δf时要考虑预估计误差的影响，使得预估计误差在Δf/2范围内。

5 仿真分析

本节通过仿真实验对本文所提出的基于频率预估计的正交匹配追踪(Frequency pre-estimation Orthogonal Matching Pursuit, F-OMP)算法进行分析与验证。先对频率进行预估计，并按文中所述，利用预估计的结果结合OMP算法的迭代过程求解。假设信号长度N=512，在预估计出每个频率附近选取Δf=5 MHz范围内等间隔划分，每个子字典的长度q=50，并定义频率估计的均方根误差(Root Mean Square Error, RMSE)如式(12)所示

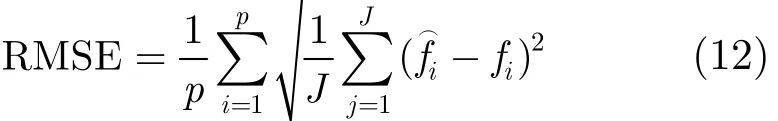
仿真实验1 选取5个频率分别为9.5 MHz, 23.6 MHz, 44.3 MHz, 56.7 MHz和67.1 MHz的单载频信号，信噪比为15 dB。采用ESPRIT算法进行频率预估计。图1给出了频率的估计结果，并与信号的真实频率进行了比较。从图1的结果可以看出F-OMP算法可以对多个窄带信号频率进行有效地估计。为了进一步验证算法的性能，在不同信噪比下比较ESPRIT算法，OMP算法以及F-OMP算法的频率估计均方根误差，其中ESPRIT算法中数据段数为32, OMP算法中则是直接在整个频率范围内建立频率间隔为0.1 MHz的过完备字典，而F-OMP算法则是先利用ESPRIT算法进行预估计，然后在预估计频率附近建立频率间隔为0.1 MHz的局部过完备字典。仿真中SNR从-5～25 dB，每隔1 dB取一个值，每个信噪比下选取3个频率不同的信号，频率从0～100 MHz内随机取值，进行1000次蒙特卡罗实验，得到3种算法频率估计均方根误差随信噪比的变化曲线如图2所示。

从图2的仿真结果可以看出，ESPRIT由于利用了信号子空间信息，在高信噪比时相对于OMP算法具有较小的频率估计均方根误差，而在低信噪比区间信号子空间估计偏差较大，得到的频率估计均方根误差也明显增大。OMP算法没有利用信号子空间信息，而是利用原子之间的相关性寻找最佳匹配原子，其均方根误差随信噪比变化较为平缓，不像ESPRIT算法那样敏感。F-OMP算法由于利用了频率预估计的结果，所以在高信噪比区间性能优于OMP算法，而在低信噪比区间则利用了类似于OMP算法计算相关性的迭代过程，所以改善了ESPRIT对信噪比的敏感性。因此，F-OMP算法在不同的信噪比均方根误差都相对较小，能够达到良好的估计性能。

仿真实验2 现在考虑算法在信号频率相距较近情况下的估计性能，选取一个信号频率固定为71.3 MHz，另一个信号频率在此基础上每隔0.5 MHz取一个值，每隔频率间隔上进行1000次蒙特卡罗实验，图3和图4分别给出了SNR=15 dB和SNR=5 dB时ESPRIT和F-OMP算法(仍采用ESPRIT算法进行频率预估计)在不同频率间隔下的均方根误差。

从图3和图4的结果可以看出，两个信号的频率相距越近，均方根误差越大。在高信噪比的条件下ESPRIT算法和F-OMP算法的频率分辨能力差异不大，在频率相距较近时仍具有较高的估计精度，而当信噪比较低时，ESPRIT算法的分辨能力下降较为明显(0.5 MHz时已无法分辨，故在图4中没有显示)，而F-OMP算法则受信噪比影响较小，当信号频率相距较近时仍然具有较小的均方根误差，估计性能较好。

仿真实验3 当信噪比较低时，频率估计算法的稳健性会受到较大影响，可能会导致频率估计错误，为了验证算法的稳定性，SNR从-20～15 dB，每隔3 dB取一个值，每个信噪比下选取3个频率不同的信号，频率从0～100 MHz内随机取值，进行1000次蒙特卡罗实验，统计ESPRIT, OMP以及F-OMP 3种算法的估计成功次数(3个信号频率全部估计正确，且误差在0.5 MHz以内才算成功)，计算每个信噪比下的成功概率，得到估计成功概率随信噪比变化曲线如图5所示。

从图5的结果可以看出，由于低信噪比的情况下，ESPRIT信号子空间估计偏差较大，估计成功概率较低，而依靠计算原子相关性的OMP算法和F-OMP算法更为稳健。F-OMP算法在迭代过程中利用了残差向量中频率的预估计值和已估计出的频率值进行正交投影更新下一次迭代的残差向量，因此，在一定程度上较OMP算法具有更稳健的性能。

6 结束语

信号的频率估计在电子侦察中有着重要的研究意义。本文针对窄带信号频率估计问题，提出了一种基于稀疏分解的频率估计算法。在预先估计出的频率附近建立冗余字典，有效地降低了字典的长度和稀疏分解的运算量，并将频率预估计的结果应用到每次的迭代过程中，以便于更好地寻找最佳匹配原子和更新残差向量。理论分析和仿真实验表明，该方法能够达到较高的估计精度，且在低信噪比条件下也具有较为稳健的性能。

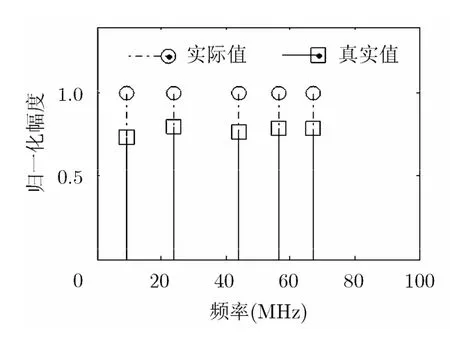
图1 频率估计结果

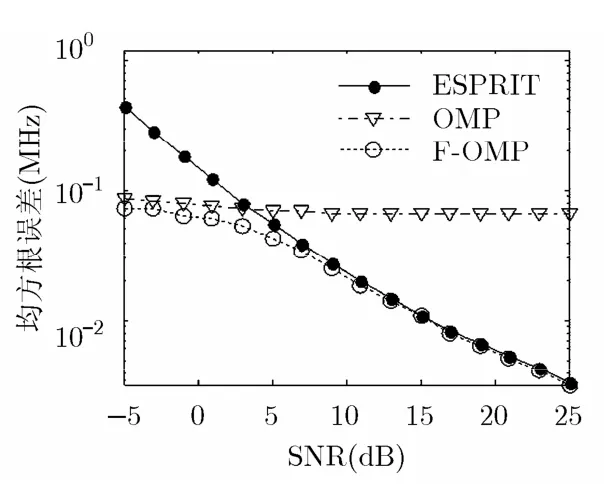
图2 频率估计均方根误差

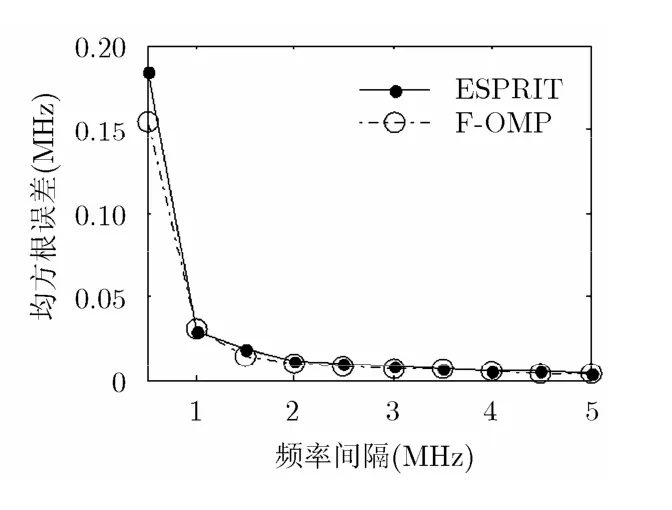
图3 不同频率间隔下的估计精度(SNR=15 dB)

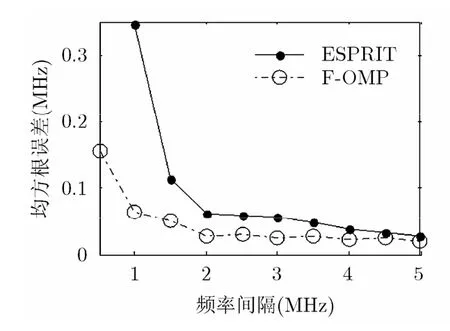
图4 不同频率间隔下的估计精度(SNR=5 dB)

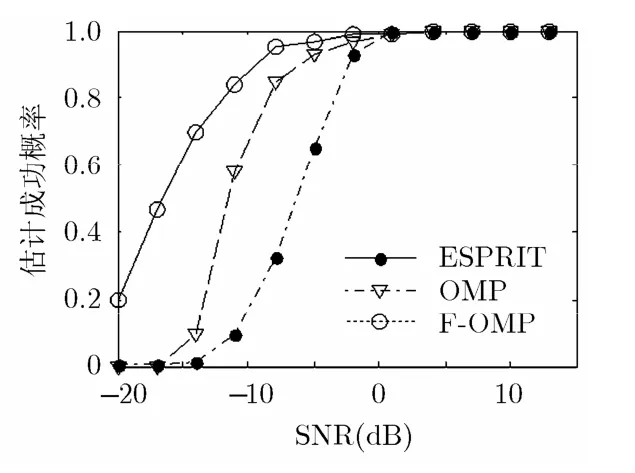
图5 不同信噪比下的估计成功概率

[1] 赵国庆. 雷达对抗原理[M]. 西安: 西安电子科技大学出版社, 1999: 13-15.

Zhao Guo-qing. Fundamentals of Radar Countermeasure[M]. Xi'an: Xidian University Press, 1999: 13-15.

[2] 王宏伟, 赵国庆, 王玉军, 等. 一种宽带数字信道化接收机[J].西安电子科技大学学报, 2010, 37(3): 487-553.

Wang Hong-wei, Zhao Guo-qing, and Wang Yu-jun, et al.. Wideband digital channelized receiver design[J]. Journal of Xidian University, 2010, 37(3): 487-553.

[3] Hasebe M, Denno S, Tomisato S, et al.. Iterative frequency offset estimation based on singular value decomposition[C]. Proceedings of the 2013 International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS), Naha, Japan, 2013: 125-130.

[4] Yamada T. High-accuracy estimation of frequency, amplitude and phase with a modified DFT for asynchronous sampling[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(6): 1428-1435.

[5] 李冰冰, 马洪帅, 刘明骞, 等. Alpha稳定分布噪声下时频重叠信号的载波频率估计方法[J]. 电子与信息学报, 2014, 36(4): 868-874.

Li Bing-bing, Ma Hong-shuai, Liu Ming-qian, et al.. Carrier frequency estimation method of time-frequency overlapped signals with alpha-stable noise[J]. Journal of Electronics & Information Technology, 2014, 36(4): 868-874.

[6] 程佩青. 数字信号处理[M]. 第3版, 北京: 清华大学出版社, 2008: 134-138.

Cheng Pei-qing. Digital Signal Processing[M]. Third Edition, Beijing: Tsinghua University Press, 2008: 134-138.

[7] Morelli M, Marchetti L, and Moretti M, et al.. Maximum likelihood frequency estimation and preamble identification in OFDMA-based Wimax systems[J]. IEEE Transactions on Wireless Communications, 2014, 13(3): 1582-1592.

[8] 张贤达. 现代信号处理[M]. 第2版, 北京: 清华大学出版社, 2002: 102-112. Zhang Xian-da. Modern Signal Processing[M]. Second Edition, Beijing: Tsinghua University Press, 2002: 102-112. [9] Schmidt R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[10] Roy R and Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(7): 984-995.

[11] Gholami A. Sparse time-frequency decomposition and some applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 489-509.

[12] Liu Yin, Wu Shun-jun, Wu Ming-yu, et al.. ESPRIT matching pursuit algorithm for DOA estimation with single snapshot[C]. Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 315-318.

[13] Wang Han, Huang Jian-guo, He Cheng-bing, et al.. An efficient sparse channel estimation method with predetermined sparsity[C]. Proceedings of the Tencon 2013-2013 IEEE Region 10 Conference(31194), Xi'an, China, 2013: 1-5.

[14] Sadeghipoor Z, Babaie-Zadeh M, Jutten C, et al.. Dictionary learning for sparse decomposition: a new criterion and algorithm[C]. Proceedings of the 2013 International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, Canada, 2013: 5855-5859.

[15] Peyre X G. Best basis compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2613-2622. [16] Rauhut H, Schnass K, and Vandergheynst P. Compressed sensing and redundant dictionaries[J]. IEEE Transactions on Information Theory, 2008, 54(5): 2210-2219.

[17] 曾小东, 曾德国, 张文超, 等. 基于OMP-SVD的多分量单频信号频率估计[J]. 雷达科学与技术, 2011, 9(2): 188-195.

Zeng Xiao-dong, Zeng De-guo, Zhang Wen-chao, et al.. Frequency estimation of multi-component signal frequency signal based on OMP-SVD[J]. Radar Science and Technology, 2011, 9(2): 188-195.

[18] 刘兆霆, 何劲, 刘中, 等. 基于压缩感知的高分辨频率估计[J].信号处理, 2009, 25(8): 1252-1256.

Liu Zhao-ting, He Jin, Liu Zhong, et al.. High resolution frequency estimation with compressed sensing[J]. Signal Processing, 2009, 25(8): 1252-1256.

[19] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[20] Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

沈志博： 男，1986年生，博士生，研究方向为电子战信号处理.

董春曦： 男，1970年生，博士，副教授，研究方向为无源侦察技术、高分辨雷达干扰技术等.

黄 龙： 男，1988年生，博士生，研究方向为电子战系统仿真.

赵国庆： 男，1953年生，硕士，教授，博士生导师，研究方向为电子侦察、无源定位等.

A Frequency Estimation Algorithm of Narrow-band Signal Based on Sparse Decomposition

Shen Zhi-bo Dong Chun-xi Huang Long Zhao Guo-qing
(Key Laboratory of Electronic Information Countermeasure and Simulation, Ministry of Education, Xidian University, Xi'an 710071, China)

For the frequency estimation problem of narrow-band multi-component signal, a frequency estimation algorithm based on the sparse decomposition is proposed, which simultaneously estimates the frequency of multiple narrow-band signal. Firstly, the pre-estimation is used to get the pre-estimating frequency by using the traditional method. Then the redundant dictionary is established by using the pre-estimating frequency to obtain a sparse representation of the signal. Finally, the precise frequency estimation is achieved by the matching pursuit algorithm. The algorithm can greatly reduce the length of dictionary and the computational complexity of sparse decomposition. The proposed algorithm can provide more accurate estimation results when updating residual vector by using the global information in an iterative process, and the performance is robust in lower SNR. The simulation results verify the effectiveness and correctness of the proposed algorithm.

Signal processing; Frequency estimation; Sparse decomposition; Redundant dictionary; Sparse representation

TN971

： A

：1009-5896(2015)04-0907-06

10.11999/JEIT140878

2014-07-02收到，2014-09-19改回

国家部委基金，中央高校基本科研业务费专项基金(JB140203)和国家973计划项目(613181)资助课题

*通信作者：董春曦 chxdong@mail.xidian.edu.cn